具备检错和纠错性能的可重构可存储的混沌逻辑运算
2023-12-18许葛亮幸世亮叶松邓加祈张曼
许葛亮,幸世亮,叶松,邓加祈,张曼
(1 巢湖学院 电子工程学院,合肥 238000)
(2 景德镇学院 机械电子工程学院,景德镇 333000)
0 引言
激光混沌信号对系统的初始条件和外界干扰极度敏感,具有非周期性和高度随机性的特点,这使其在混沌保密通信中有着广泛的应用,如混沌激光雷达、高速物理随机数发生器、高速密钥分发等[1-4]。作为产生混沌激光信号的理想光源,垂直腔表面发射激光器(Vertical Cavity Surface Emitting Laser,VCSEL)具有体积小、阈值电流低、动态调制频率高、发散角度小、易于实现二维阵列等优点[5-7]。由于VCSEL 的激光腔结构为匀称的圆形,其内部增益介质的各向异性很弱,这导致了激光器会产生两个相互正交的线性偏振模,即横电模和横磁模,分别用x偏振分量(xPolarization Component,x-PC)和y偏振分量(yPolarization Component,y-PC)表示。其在光注入、光反馈或光电反馈的作用下能激射高维混沌态的x-PC 和y-PC[8-9]。并且通过改变泵浦电流,光注入强度或注入光的频率失谐能诱导VCSEL 产生丰富的动力学行为如偏振转换以及偏振双稳态[10-18]。目前,这些现象普遍适用于一些备受关注的领域,例如混沌计算。
2010 年,MASOLLER C 通过偏振双稳态数值实现了随机逻辑门[5];2012 年,又提出了利用噪声和光注入VCSEL 的偏振双稳态实现随机逻辑门的方案[6];2013 年,利用可调谐光注入VCSEL 的方法再次实现了全光随机逻辑门[7]。钟东洲在混沌计算领域也取得了大量的创新性成果[19-21]:2015 年,基于电光效应和偏振双稳态实现了光电复合逻辑门;2016 年,基于广义混沌同步和偏振双稳态,实现了全光随机逻辑门及其延时存储;2017 年,提出了让VCSEL 受取样光栅分布布拉格反射可调谐激光器的光注入的实验方案,实现了可重构的全光混沌逻辑门。2021 年,基于电光调制本课题组也实现了可重构的混沌逻辑运算,运算速率达到皮秒量级,且系统结构简单易于集成[22]。
近些年,激光混沌同步的快速发展也引起了人们的广泛关注。2013 年,颜森林基于激光混沌并联同步实现了全光非门、或非门以及同或门[23];2014 年,又利用三个混沌激光器的并行同步实现了光电逻辑NOR和XNOR 门[24]。2021 年,李璞等数值分析了在一定的参数失配范围内,两个自由运行的VCSELs 在平行注入和正交注入两种互耦合结构下实现了高质量混沌同步[25];2023 年,又进一步研究了相互耦合的自由运行VCSELs 在平行注入和正交注入两种情况下的偏振混沌的超前-滞后同步[26]。2022 年,钟东洲等基于光学储备池实现了高质量的混沌同步[27]。要获得完全混沌同步,就必须要求驱动系统和响应系统在结构组成上完全对称,并且两系统参数要完全匹配。外界干扰会影响混沌信号,还可能引起系统参数发生漂移,使得驱动系统参数与响应系统参数失配,最终导致系统的混沌同步质量产生剧烈震荡。因此当混沌同步应用于混沌计算时,可能由于混沌同步质量的不稳定导致计算出现差错。
上述大部分方案实现的是静态的混沌逻辑运算,具备检错和纠错性能的可重构可存储功能的混沌逻辑运算发展还比较滞后。基于驱动-响应VCSELs 的高维混沌系统,不仅具有丰富的模式,还能实现混沌同步的稳定操控,这为实现可重构可存储的混沌逻辑运算创造了可能。然而还有很多基础科学问题需要解决,如混沌同步对系统关键参数的依赖性、VCSEL 输出混沌态激光对系统参数的要求、逻辑控制信号的选择、逻辑运算与VCSEL 关键参数的约束关系、噪声对混沌同步质量的影响,以及计算出现差错时如何进行有效检错等。受这些问题的激励,在驱动-响应VCSELs 混沌系统里,基于电光调制理论,本文探索了驱动VCSEL(Drive VCSEL,D-VCSEL)和响应VCSEL(Response VCSEL,R-VCSEL)的输出偏振光动力学状态和同步质量随外加电场和归一化注入电流参数的演变,并进一步给出了重构和存储混沌逻辑运算如AND、NAND、OR、NOR、XOR 及XNOR 的实现步骤,最后阐述了混沌逻辑运算的检错和纠错性能。
1 理论与模型
驱动-响应VCSELs 混沌系统装置图如图1。其中D-VCSE 和R-VCSEL 的中心波长均为1 550 nm,光纤隔离器(Fiber Isolator,FI)的作用是保持光的单向传输,中性密度滤光镜(Neutral density Filter,NDF)用于控制光的注入强度,平面镜(Mirror,M)用于调整的光的传输方向,光电探测器(Photodetector,PD)用于把光信号转换为电信号。D-VCSEL 输出的光通过FI1,然后被光纤分束器1(Fiber Beam Splitter,FBS1)分为光束l1和光束l2。光束l2通过FBS2被分成光束l3和光束l4。光束l4通过光纤偏振分束器1(Fiber Polarization Beam Splitter,FPBS1)被分离出偏振分量x-PCD2和偏振分量y-PCD2。其中x-PCD2直接注入周期性极化铌酸锂1(Periodic Poled LiNbo3,PPLN1)晶体中,y-PCD2通过法拉第旋转器1(Faraday Rotator,FR1)和半波片1(Half Wave Plate,HWP1)后被注入到PPLN1晶体中。FR1和HWP1的作用是转换y-PCD2的偏振方向至晶体的z轴方向。注入到晶体中的x-PCD2和y-PCD2分别作为o 光和e 光的初始输入。从PPLN1晶体输出的x-PC 和y-PC(e 光通过FR3 和HWP3 转化成y-PC)被光耦合器1(Optic Coupler,OCP1)耦合在一起,并过NDF1和FI2后被注入到D-VCSEL。光束l1被FPBS4分离出x-PCD1和y-PCD1;同理,光束l3被FPBS2分离出x-PCD3和y-PCD3,x-PCD3被注入到PPLN2中,y-PCD3通过FR2和HWP2后也被注入到PPLN2。从PPLN2输出的x-PC 和y-PC(e 光通过FR4 和HWP4 转化成y-PC)被光耦合器2(OCP2)耦合在一起,并通过NDF2和FI3后被注入到R-VCSEL 中。来自R-VCSEL 的光束被FPBS3分离出x-PCR和y-PCR。D-VCSEL 输出的光在反馈腔往返一次的时间以及传输至R-VCSEL 所经历的时间为分别为τ和τc,两时延差τT=τc-τ。
在可重构可存储的混沌逻辑运算的实现方案中,D-VCSEL 的归一化注入电流被调制为逻辑输入,外加电场被调制为逻辑控制信号,逻辑输出Z1和Z2根据D-VCSEL 输出的偏振光(x-PCD1和y-PCD1)与R-VCSEL 输出的偏振光(x-PCR和y-PCR)的同步质量进行解调。值得注意的是,采用阈值机制分别对x-PCD1和x-PCR进行解调也能获得相同的逻辑输出Z3和Z4(如图1)。假设x-PCD1和x-PCR有相同的阈值并用A*表示。每一比特位时间内x-PCD1强度的均值和x-PCR强度的均值分别被定义为ADx和ARx。为了实现混沌逻辑运算的重构和存储操作,提出如下技术步骤:
1)首先,计算偏振光x-PCD1与x-PCR,以及y-PCD1与y-PCR的同步质量在归一化注入电流和外加电场参数空间内的演变。
2)根据同步质量的演变规律,确定归一化注入电流的合适取值用于调制逻辑输入,以及选择外加电场的合适取值用于调制逻辑控制信号。
3)让逻辑控制信号和逻辑输入动态地满足不同的逻辑运算关系,如AND、NAND、OR、NOR、XOR 和XNOR。
4)计算每一比特位持续时间内x-PCD1强度的均值ADx和x-PCR强度的均值ARx,x-PCD1与x-PCR的同步质量以及y-PCD1与y-PCR的同步质量。
5)根据同步质量和阈值机制,解调获得逻辑输出Z1、Z2、Z3和Z4。若x-PCD1与x-PCR达到完全混沌同步,Z1=0,若不完全混沌同步,则Z1=1;同理若y-PCD1与y-PCR实现完全混沌同步,Z2=0,若同步质量差,则Z2=1。如果ADx-A*>0,Z3=1,ADx-A*≤0,则Z3=0;同理对于ARx若有ARx-A*>0,Z4=1;反之,则Z4=0。当Z1(t)=Z2(t)=Z3(t)=Z4(t+τT)时,即实现了混沌逻辑运算的延时存储。
为了实现可重构的混沌逻辑运算,逻辑控制信号与逻辑输入需满足不同的逻辑运算关系。因此逻辑控制信号需随着逻辑输入的变化而变化。如何实现逻辑控制信号和逻辑输入同步变化是一个关键问题。为了克服该问题,提出如下解决方案。时变电流源1(S1)和S2能输出6 路经归一化处理的方波电流μ1、μ2、μ3、μ4、μ5和μ6(如图1),且μ1=μ3=μ5、μ2=μ4=μ6。此处D-VCSEL 的归一化注入电流μD=μ1+μ2,R-VCSEL 的归一化注入电流μR=μ3+μ4,所以μD=μR,μ1和μ2分别被调制为逻辑输入I1和I2,同时μ5和μ6分别被调制为电子逻辑计算器(Electronic Logic Calculator,ELC)的两电逻辑输入i1和i2,因此逻辑输入(I1,I2)与(i1,i2)总保持逻辑同步。ELC 的逻辑输出Y可通过外加电场控制器(Applied Electric Field Controller,AEFC)来设置外加电场ED和ER的数值,当Y=0 时,ED=ER=E01,逻辑控制信号Cf=0,当Y=1 时,ED=ER=E02,Cf=1,E01和E02是外加电场的两个可能取值。由于使用ELC 可以让Y与(i1,i2)满足不同的逻辑运算关系如AND、NAND、OR、NOR、XOR 和XNOR。因此Cf可以间接同(I1,I2)满足不同的逻辑运算。针对每种逻辑运算,逻辑控制信号Cf同逻辑输入发生同步改变。因此通过转换逻辑控制信号和逻辑输入的逻辑关系,可重构的混沌逻辑运算将有望被实现。
基于VCSEL 的自旋翻转模型[15],当D-VCSEL 受到来自PPLN1 晶体光的延时反馈时,其动力学行为方程可表示为
同理,对于R-VCSEL,其受到PPLN2晶体输出光的延时注入,其速率方程可表示为
式(1)~(6)中,E表示光的复振幅;下标D、R、x和y分别表示D-VCSEL、R-VCSEL、x-PC 和y-PC;EP1x和EP1y分别表示PPLN1晶体输出的x-PC 和y-PC 的复振幅;同理EP2x和EP2y分别表示PPLN2晶体输出的x-PC 和y-PC 的复振幅;*表示共轭运算符;N表示反转载流子数目;μD和μR分别表示D-VCSEL 和RVCSEL 的归一化注入电流;n为上、下旋通道载流子浓度差;βsp为自发辐射因子;ζx和ζy是一对相互独立且服从标准正态分布的高斯白噪声;k表示场衰减速率;a为线宽增强因子;γs表示自旋弛豫速率;γa表示二向色性;γp为双折射率;γe表示非辐射载流子弛豫速率;kf和kinj表示光反馈强度和光注入强度;D是噪声强度参数且。
注入到PPLN1晶体中的x-PC 和y-PC,作为晶体中o 光和e 光的初始输入,它们的振幅满足
同理,在PPLN2 晶体中有
晶体的长度为L,电光调制过程中PPLN1和PPLN2中的o 光和e 光的动力学方程分别为
经电光调制后从PPLN1输出的x-PC 和y-PC 满足
同理从PPLN2 输出的x-PC 和y-PC 满足
式(7)~(12)中,下标o/e 分别表示o 光和e 光;ℏ 表示普朗克常量;TL表示光在激光腔内往返一次的时间,且TL=2ngvc/Lv,vc表示光在真空中的传播速度,ng表示有源层有效折射率,Lv表示激光腔长度;SA表示光斑有效面积;n1和n2分别表示o 光和e 光的有效折射率;ω0为D-VCSEL 和R-VCSEL 的中心频率;V表示有源层体积。
2 分析与讨论
根据表1 中的系统参数,采用四阶龙格库塔法来对方程(1)~(12)进行计算。在驱动-响应VCSELs 混沌系统中,为了量化x-PCD1同x-PCR,以及y-PCD1和y-PCR间的混沌同步质量,引入相关函数ρx,y,并定义
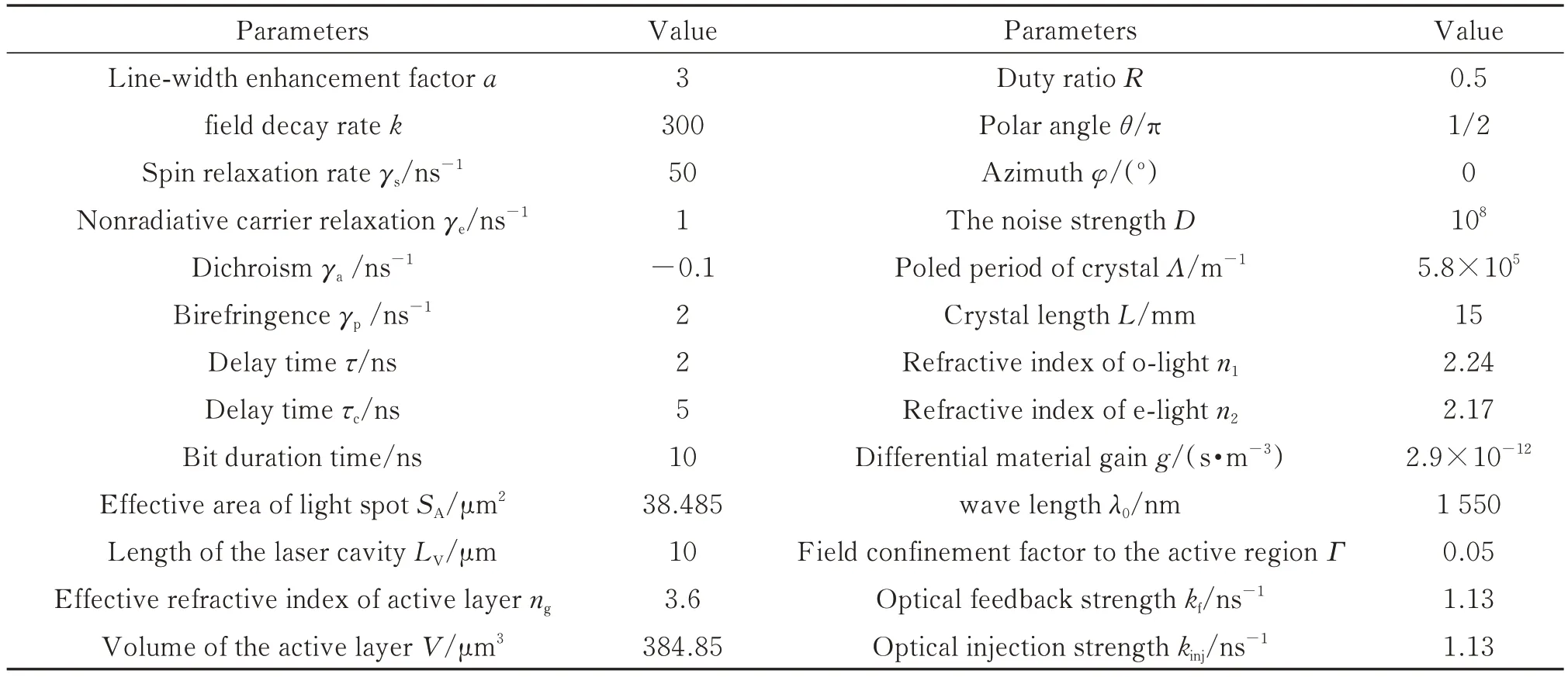
表1 系统主要参数Table 1 Main system parameters
式中,下标Dx,Dy,Rx和Ry分别表示x-PCD1,y-PCD1,x-PCR和y-PCR;I表示光强且IDx,Dy(t)=|EDx,Dy(t)|2,IRx,Ry(t)=|ERx,Ry(t)|2,τT=τc-τ;符号< >表示求时间均值;x-PCD1与x-PCR的同步误差用SEx(t)表示,且SEx(t)=IDx(t)-IRx(t+τT)表示;同理y-PCD1与y-PCR的同步误差SEy(t)=IDy(t)-IRy(t+τT)表示;ρx,y的取值范围均在0 到1 之间,且它们的取值越大表明混沌同步质量越高,同步误差越小。当ρx,y=1 时,SEx(t)=SEy(t)=0,表明实现了完全混沌同步,即有
为了确保D-VCSEL 和R-VCSEL 能实现混沌态输出,即x-PCD1、y-PCD1、x-PCR和y-PCR处于混沌态,计算了它们在参数空间ED和μD内的动力学状态演变,结果如图2。从图中可看出x-PCD1、y-PCD1、x-PCR和y-PCR在参数空间内演变会呈现出混沌态(Chaotic State,CS)和准周期态(Quasi-Periodic State,QPS)。这里,我们只关注混沌态参数区域。图2(a)中,μD在区间1~1.49,ED在区间0.04~0.25 kV/mm,或0.3~0.53 kV/mm,或0.62~0.87 kV/mm,或0.91~1 kV/mm 变化时,x-PCD1均为混沌态。图2(b)中,当ED大于0.021 kV/mm 时,y-PCD1均处于混沌态。图2(c)中,μD在1~1.49 区间内变化,且ED位于区间0~0.26 kV/mm,或0.33~0.53 kV/mm,或0.58~0.87 kV/mm,或0.92~1 kV/mm 时,x-PCR为混沌态。图2(d)中,ED在区间0.03~1 kV/mm 变化时,y-PCR均处于混沌态。
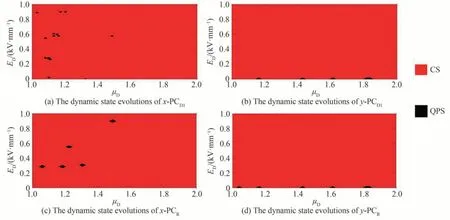
图2 偏振光x-PCD1、y-PCD1、x-PCR和y-PCR在参数空间ED和μD内的动力学状态演变Fig.2 Dynamic state evolutions of polarized light x-PCD1,y-PCD1,x-PCR and y-PCR in the parameter space ED and μD
由于混沌逻辑运算的实现还依赖于偏振分量的混沌同步质量,因此研究系统关键参数对混沌同步质量的影响很有必要。首先计算了相关函数在参数空间外加电场和归一化注入电流内的演变,如图3。从图中可以看出ρx和ρy的演变轨迹大致相同,例如当电流小于1.2 时,随着外加电场的逐渐增大,相关函数ρx和ρy较小且在0~1 间快速振荡,表明两偏振分量的同步质量差且不稳定;当电流大于1.3 时,两偏振分量的完全混沌同步随外加电场从0 逐渐增大到1 而表现出准周期性的变化,如ED在区间0.01~0.1 kV/mm,或0.21~0.37 kV/mm,或0.5~0.68 kV/mm,或0.8~0.98 kV/mm 变化时,相关函数ρx和ρy恒为1。
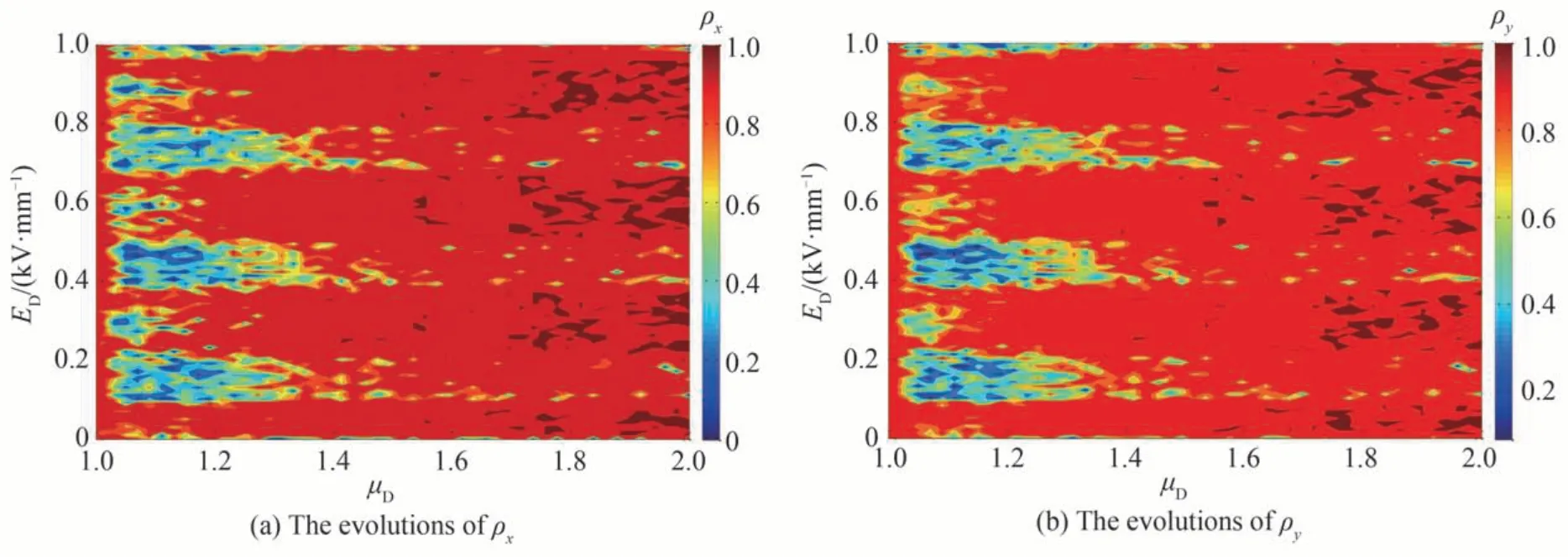
图3 相关函数在参数空间外加电场和归一化注入电流内的动态演变Fig.3 Dynamic evolutions of the correlation function within the parameter space of the applied electric field and the normalized injection current
为了找到外加电场和归一化注入电流的合适取值用于调制逻辑控制信号和逻辑输入,进一步计算了相关函数在图3 中的局部变化,结果如图4。研究了外加电场的几个特殊值如0.434 3 kV/mm、0.583 kV/mm、0.73 kV/mm 和1 kV/mm 条件下,相关函数ρx和ρy随归一化注入电流的演变曲线。从图4 可以看出当外加电场为0.434 3 kV/mm 或0.73 kV/mm 或1 kV/mm 时,ρx和ρy随归一化注入电流的增大均表现出较为剧烈的振荡,且外加电场为0.73 kV/mm 时曲线振荡的幅度更大,表明同步质量差且更不稳定。如果外加电场固定在0.583 kV/mm,归一化注入电流在1.3~2 范围内变化时,ρx和ρy的值恒为1,此时偏振分量实现了完全混沌同步;若电流小于1.3,ρx和ρy均出现快速波动,表明偏振分量的同步质量较差。因此根据第1 节步骤5)的解调规则,归一化注入电流应大于1.3,且外加电场可以选取0.583 kV/mm 和0.73 kV/mm 来实现偏振分量的完全混沌同步和不完全混沌同步两种情形。
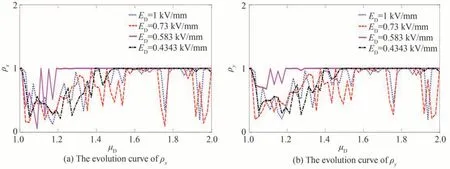
图4 外加电场分别为0.434 3、0.583、0.73、1 kV/mm 时,相关函数随归一化注入电流的演变曲线Fig.4 The evolution curves of the correlation function with the change of the normalized injection current when the applied electric field is 0.434 3 kV/mm,0.583 kV/mm,0.73 kV/mm and 1 kV/mm
假设归一化注入电流μD等于两方波电流之和即μD=μ1+μ2,μ1和μ2分别被调制为逻辑输入I1和I2。由于逻辑输入(I1,I2)存在四种组合:(0,0)、(0,1)、(1,0)和(1,1),利用三级信号μDI,μDⅡ和μDⅢ来表示这四种逻辑输入组合,即μDⅡ代表(0,1)和(1,0),μDI表示(0,0),以及μDⅢ等同于(1,1)。μD的三种可能取值,即三级信号μDI、μDⅡ和μDⅡI在一个比特位时间T内均为常数。T被设定为10 ns。根据混沌态和相关函数在参数空间内的演变规律,设μDI=1.544,μDⅡ=1.546,μDⅢ=1.548。因此当μ1=μ2=0.772 时I1=I2=0;μ1=μ2=0.774 时I1=I2=1。外加电场ED被调制为逻辑控制信号Cf且假设ED=0.73 kV/mm 时,Cf=1;ED=0.583 kV/mm 时,Cf=0。
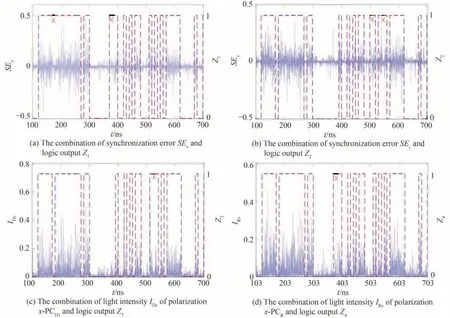
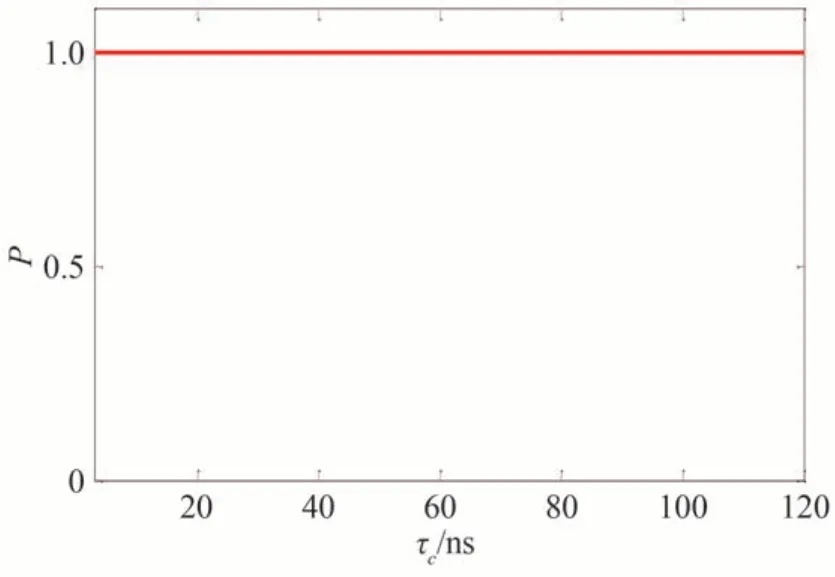
根据步骤5),逻辑输出Z3和Z4依赖于x-PCD1和x-PCR的阈值A*。如何找到A*的合适取值对逻辑输出的判定至关重要。为了解决这个问题,考虑Cf与I1和I2能满足不同的逻辑运算关系如AND、NAND、OR、NOR、XOR 和XNOR。针对上述各种逻辑运算关系,分别计算出Cf=0 时偏振分量x-PCD1和x-PCR强度的最大均值ADxmax和ARxmax,以及Cf=1 时x-PCD1和x-PCR强度的最小均值ADxmin和ARxmin,具体如表2。从表中不难发现,阈值A*满足条件(ADxmax,ARxmax)max 通过执行步骤3)~5),实现了混沌逻辑运算的重构和存储操作,如图5。图5(a)为外加电场ED(逻辑控制信号Cf)与归一化注入电流μD(逻辑输入I1和I2)的组合;图5(b)展示了同步误差SEx与逻辑输出Z1的组合;图5(c)展示了同步误差SEy与逻辑输出Z2的组合;图5(d)给出了偏振x-PCD1的光强IDx与逻辑输出Z3的组合;图5(e)给出了偏振y-PCD1的光强IRx与逻辑输出Z4的组合。从图5 和表2 可知,时间t在100~200 ns 内Cf满足逻辑运算Cf=I1+I2,当(I1,I2)分别为(0,1)、(1,0)和(1,1)时,ADxmin=0.027>A*,ARxmin=0.022>A*,SEx(t)和SEy(t)均恒不为0,因此可得到Z1(t)=Z2(t)=Z3(t)=Z4(t+τT)=1;当(I1,I2)=(0,0)时,ADxmax=2.5×10-4 图5 可重构可存储的混沌逻辑计算OR、NAND、AND、XNOR、XOR 和NORFig.5 Reconfigurable and storable chaotic logic OR,NAND,AND,XNOR,XOR and NOR operations 图6 噪声强度D=1×109对逻辑输出Z1、Z2、Z3和Z4的影响Fig.6 Effect of noise strength D=1×109 on logic outputs Z1,Z2,Z3 and Z4 为了提升Z1和Z2的抗噪声性能,采取如下的方案:设同步误差SEx和SEy有相同的阈值M*,分别用Mx和My表示每一比特位时间内SEx和SEy的均方差。针对Cf与I1和I2满足不同的逻辑运算关系,计算出Cf=0 时SEx和SEy的均方差的最大值Mxmax和Mymax,以及Cf=1 时SEx和SEy的均方差的最小值Mxmin和Mymin,如表3,噪声强度取109。从表中可得所有Mxmax的最大值为2.15×10-4,所有Mymax的最大值为5.38×10-4,所有Mxmin的最小值为7.75×10-4,以及所有Mymin的最小值为0.001 3。阈值M*满足(Mxmax,Mymax)max 表3 针对Cf与逻辑输入满足不同的逻辑运算,Cf=0 时SEx和SEy均方差的最大值以及Cf=1 时SEx和SEy均方差的最小值Table 3 Maximum of the mean square errors of SEx and SEy when Cf=0 and minimum of the mean square errors of SEx and SEy when Cf=1 for different logic operations that Cf and the logic inputs satisfy 进一步研究了噪声强度为1.77×109对逻辑运算的影响,结果如图7。从图7(a)、(b)可以看出x-PCD1和x-PCR,y-PCD1和y-PCR因噪声无法实现完全混沌同步,但是由于采用阈值机制,逻辑输出Z1和Z2进行解码时没有产生误码。逻辑输出Z3和Z4依然保持良好的抗噪声性能,实现正确解码。 当噪声强度增至1.84×109时,逻辑运算受噪声的影响如图8。从图中可以看出逻辑输出Z1产生了两处解码错误,逻辑输出Z2产生了四处解码错误,且均是“0”码误译成“1”码。产生解码错误的主要原因是噪声使得同步误差发生剧烈振荡,在比特位持续时间内同步误差的均方差大于阈值,导致逻辑输出译为“1”码。逻辑输出Z3和Z4依然没有产生误码,由此可以得出逻辑输出Z3和Z4的抗噪声要优于Z1和Z2的抗噪声性能。 图8 噪声强度D=1.84×109对逻辑输出Z1、Z2、Z3和Z4的影响Fig.8 Effect of noise strength D=1.84×109 on logic outputs Z1,Z2,Z3 and Z4 图9 展示了噪声强度为1.89×109对逻辑运算的影响。从图中可以看出逻辑输出Z1和Z2分别有两处误码,Z3和Z4分别有一处误码,所以在此噪声强度下逻辑运算失效。 图9 噪声强度D=1.89×109对逻辑输出Z1、Z2、Z3和Z4的影响Fig.9 Effect of noise strength D=1.89×109 on logic outputs Z1,Z2,Z3 and Z4 综上可得通过采用阈值机制来解调逻辑输出,能有效地增强逻辑运算的抗噪声性能。噪声强度在1.77×109范围内对逻辑运算不会产生影响。噪声强度在1.84×109范围内不会对逻辑输出Z3和Z4产生影响,在这种情况下将Z3、Z4分别同Z1、Z2比较就能实现对Z1、Z2的检错和纠错处理。当噪声强度超过1.89×109时逻辑输出Z1、Z2、Z3和Z4均会产生误码,逻辑运算失效,逻辑输出也丧失了检错和纠错的性能。 最后探讨不同的时延τc对逻辑输出Z4的成功概率的影响。成功概率的定义为正确的码元数目与总的码元数目的比值,这里的噪声强度为109。数值仿真结果如图10。结果表明时延τc在~120 ns 范围内变化时,逻辑输出Z4的成功概率恒为1,即逻辑输出Z4不会产生误码。逻辑输出Z4能正确输出的原因在于外加电场为0.583 kV/mm 时,系统实现了完全混沌同步,此时时延τc不会影响同步质量[28],因此逻辑输出Z4可以成功地延时存储逻辑输出Z3中的“0”码。当外加电场为0.73 kV/mm 时,τc在一定范围内变化时,系统始终处于不完全混沌同步状态[28],根据阈值机制能成功解调出Z4中的“1”码。因此时延τc在3~120 ns 范围内变化时不会对逻辑运算的延时存储产生影响。 图10 成功概率P 随时延τc的演变Fig.10 The evolution of the success probability P with the time delay τc 本文提出了一种具备检错和纠错性能的可重构可存储的混沌逻辑运算的实现方案。利用驱动-响应垂直腔面发射激光器混沌系统,系统参数外加电场和归一化注入电流分别被调制为逻辑控制信号和逻辑输入,逻辑输出Z1、Z2、Z3和Z4均采用阈值机制进行解调。转换逻辑控制信号和逻辑输入的运算关系,系统就能实现混沌逻辑运算如AND、NAND、OR、NOR、XOR 和XNOR 的重构和存储操作。研究发现当噪声强度在1.77×109范围内时,逻辑输出不会产生误码。当噪声强度达到1.84×109时,逻辑输出Z1、Z2产生误码,但逻辑输出Z3和Z4保持正确地输出。如果噪声强度达到1.89×109,逻辑输出Z1、Z2、Z3和Z4均出现误码,逻辑运算失效。因此Z3和Z4的抗噪声性能要优于Z1和Z2的抗噪声性能。且若噪声强度在1.84×109范围内,逻辑输出Z1、Z2可通过同Z3和Z4校对实现检错和纠错处理。并且在一定的噪声强度下,时延τc在3~120 ns 范围内变化时不会对逻辑运算的延时存储产生影响。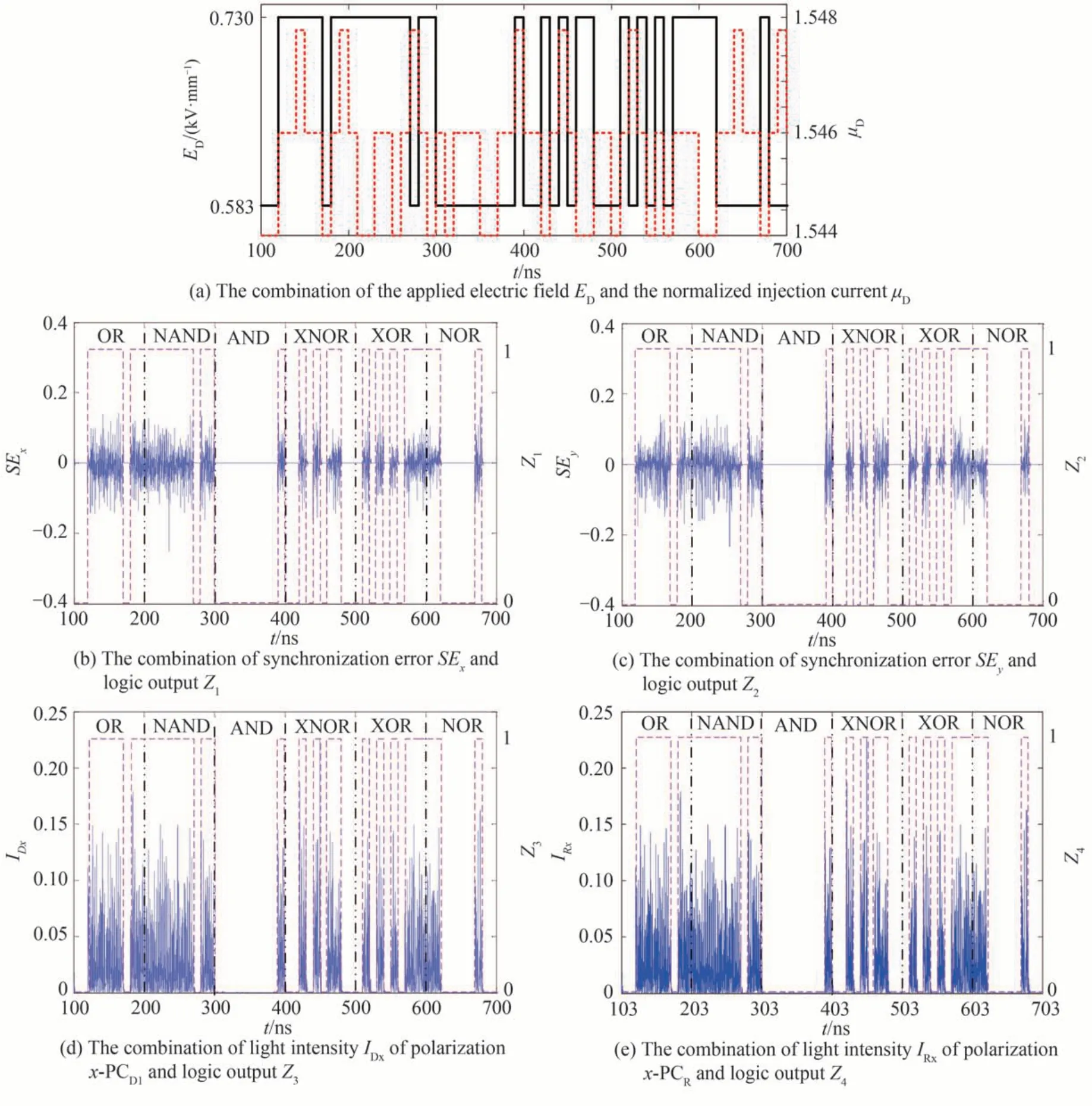
3 结论
