勒洛四面体与传统磨矿介质对料层冲击破碎特性的对比研究
2023-12-16国宏臣周强肖庆飞黄守向刘向阳李云啸王庆凯骆忠
国宏臣,周强,,肖庆飞,黄守向,刘向阳,3,李云啸,王庆凯,骆忠
1. 昆明理工大学 国土资源工程学院,云南 昆明 650093;
2. 矿冶过程智能优化制造全国重点实验室,北京 102628;
3. 矿物加工科学与技术国家重点实验室,北京 102628;
4. 玉溪矿业有限公司,云南 玉溪 653100
引言
磨矿是在机械设备中,借助于介质(钢球、钢棒、砾石)和矿石本身的冲击和磨剥作用,使矿石的粒度进一步变小,直至研磨成粉末的作业。磨矿的意义在于使矿石中的有用成分全部或者大部分单体解离并达到选别作业要求的粒度,以便为选别作业有效地回收矿石中的有用成分创造条件。磨矿作业是能耗非常高的一个工序,调查显示磨矿作业能耗一般占整个选矿厂工艺流程的30%~75%,有的甚至高达85%[1-3],因此,提高选矿厂的磨矿效率对选矿厂非常重要。影响球磨机磨矿产品粒度的因素主要有磨矿介质、介质配比、介质充填率、磨矿量、磨机类型、磨矿方式等[4-6],其中磨矿介质是最易控制的因素之一。
磨矿介质形状在产品粒度和能耗方面对球磨机性能有重大影响[7]。近年来,各种形状的磨矿介质,包括棒形、立方体、短圆柱形、短截头锥形及其他形状已被用作球的替代品。钢柱介质受到特别关注,因其同质量和尺寸与球形介质相比具有更大的表面积和更高的堆积密度[8],在钢柱介质的基础上演变出效果更好的胶囊球[9]、钢段[10]等。威布尔分布是连续性的概率分布,其概率密度为:其中,x是随机变量,λ>0 是比例参数,k>0 是形状参数,它的累积分布函数是扩展的指数分布函数,当k取不同值时表现为不同分布,其在工业制造、可靠性和失效性分析、拟合度等方面有这极为广泛的应用,可用威布尔分布来描述介质对料层冲击后粒度分布的好坏,由于它可以利用概率值很容易地推断出它的分布参数,被广泛应用于各种实验的数据处理。国内外学者已经对矿石破碎后的粒度分布规律进行了一系列研究:1927 年,Fréchet(1927)首先给出这一分布的定义;1933 年,Rosin 和Rammler 在研究碎末的分布时,第一次应用了威布尔分布[11];1951 年瑞典皇家工业大学的威布尔教授首次将威布尔分布模型用于试件在外载荷的作用下断裂失效的概率[12];刘送永等研究表明,威布尔分布和分形分布均可很好地表示煤的粒度分布规律[13];江红祥利用威布尔分布研究冲击速度对煤岩破碎能量、粒度分布的影响[14]。
磨矿作业在其破碎过程中引入了许多不同的介质形状。南非Mintek 研究所报告了使用非球形而是圆锥形的介质形状,这大大降低了铸造行业的成本,这种类型的介质形状能够提供更大的研磨表面积和更高的破损率[15-16];Cloos[17]建议研磨介质应具有较大的表面积,以便与矿石进行更多的接触;除了产生新的表面积外,进行破碎的主要目的是在所需的尺寸范围内获得尽可能多的矿料,N.Hlabangana 提出破碎超过一定尺寸范围的矿料会导致能量的浪费为无效破碎[18],因此,在这两个极端之间存在最佳平衡点,找到最佳磨矿条件对于提高矿石研磨效率至关重要。
为探究同质量的勒洛四面体介质形状(勒洛四面体是一种由四个三角形构成的四面体,它的特点是四个三角形的面积相等,四个顶点在同一球面上)比传统介质形状对料层的冲击是否有更好的粒度分布,所以进行本次实验,对不同形状(球体、勒洛四面体、圆柱体)和高度(0.5 m、1.0 m、1.5 m、2.0 m)下的介质在由钢合金砧和玻璃管组成的落重设备中进行落锤实验,经过筛分水析实验后对介质形状冲击后的矿层粒度组成进行分析,利用威布尔分布计算出铜矿破碎特性指数,验证勒洛四面体介质形状冲击效果最好。
1 威布尔分布
对于矿石破碎粒度分布规律的研究,研究者先后尝试利用标准分布、泊松分布、二项式分布、对数正态分布以及威布尔分布函数等来描述矿石冲击破碎的粒度分布,但仅有威布尔分布被大量破碎数据证实是成功的。20 世纪初期,Gates 提出利用威布尔公式分析冲击破碎产品粒度分布问题,后Rosin 和Rammler将实验数据与表达式进行大量对比,提出了威布尔分布用于描述破碎产品粒度分布的理论框架。引入威布尔分布模型来描述本文研究的矿石冲击破碎粒度分布,其可用公式(1)表示[19]:
式中:
V:矿石破碎后粒度不大于d 的碎铜矿占试样总量的比例;
d0:质量累积至总质量63.2%时的颗粒直径,其是表征破碎程度的参数,mm;
m:铜矿破碎特性指数。
为便于分析铜矿破碎粒度分布规律,将式(1)进行变化:
对式(2)两边同时开对数得:
对公式(3)进行整理得:
式中,F(d)为破碎后铜矿粒度不大于d的质量累计分布函数。
2 实验方法
2.1 介质形状
此次实验主要针对冲击结果(冲击产品的粒度分布)进行讨论。
实验变化的参数有:介质形状、冲击高度。图1显示了三种介质形状的不同的冲击方向。
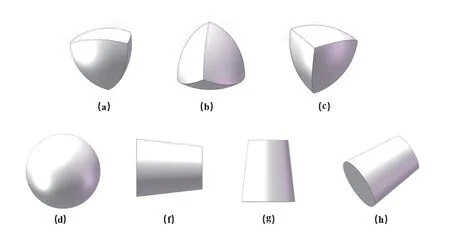
图1 落锤测试仪的冲击方向:勒洛四面体(a、b、c);球体(d);柱体(f、g、h)Fig. 1 The impact direction of the drop weight tester: Lelo tetrahedron(a, b, c); sphere(d); cylinder(f, g, h)
2.2 实验方案
对厄瓜多尔米拉多铜矿矿石进行测试,其矿石普氏硬度系数最大为20.6,硬度较硬,最小为6.85,属于中等偏软矿块,平均硬度13.3,整体属于较硬矿石,说明矿石较难磨。表1 为落重实验方案,用不同形状介质在不同高度对厄瓜多尔米拉多铜矿的150 g 料层矿样进行冲击实验。图2 显示了用作落重的不同介质形状,所有不同的介质类型都具有相同的质量。

表1 落重实验方案Table 1 Weight drop test scheme

图2 (a)钢球;(b)钢段;(c)勒洛四面体Fig. 2 (a) steel ball; (b) steel segment; (c) Leroy tetrahedron
2.3 实验过程
磨机内的介质冲击矿层行为可以通过冲击技术(如落重实验)进行模拟,通过配置不同质量的落锤、调节不同下落高度以获得相应的冲击势能,对不同颗粒大小、不同性质的矿石进行冲击实验。通过准确的实验数据获取破碎粒度与破碎能量的曲线及关系方程,判断矿石的软硬程度、颗粒尺寸对抗冲击破碎能力的影响。很多研究人员通过落重实验从根本上研究不同介质对不同矿石的破碎行为[20-21]。
使用不同形状介质(图2)在厄瓜多尔米拉多铜矿颗粒床上和由钢合金砧和常置玻璃管组成的设备(图3)中进行落锤实验。对于钢段和勒洛四面体,在整个重复测试中质量的初始方向保持不变,尽管这并不能保证每次的冲击方向相同。在实验过程中,介质被提升到所需的高度自由落体落到钢砧中心的颗粒床上,然后将颗粒床从钢砧中取出并在下一次跌落测试之前重新将颗粒床混合均匀。重复该过程50 次,然后进行筛分水析测出冲击矿样粒度组成。
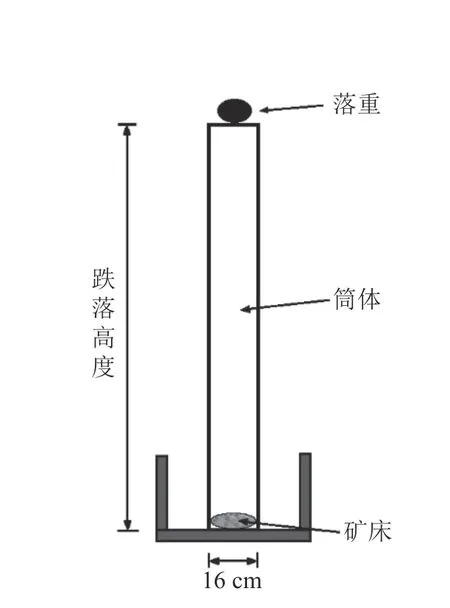
图3 落重装置示意图Fig. 3 Schematic diagram of falling weight device
3 实验结果分析
在冲击速度分别为3.13、4.43、5.42、6.29 m/s 的情况下,其质量累积分布产率见表2 所示。

表2 铜矿冲击破碎产品质量累积概率Table 2 Cu ore impact crushing product quality cumulative probability
从表2 中可看出,随着高度的提升勒洛四面体介质对矿石能够进行有效的冲击破碎,在产品粒度组成中可得到体现。冲击高度达到2 m 时可明显看出勒洛四面体介质的优势。如图4 所示其表达式为:
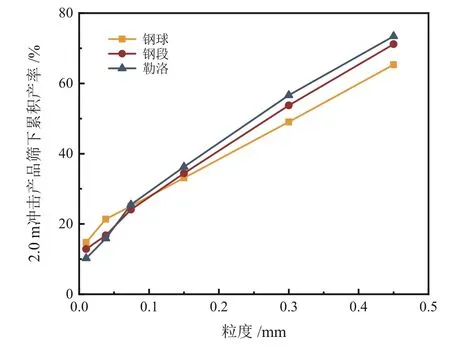
图4 2.0 m 跌落高度累积筛下曲线Fig. 4 Cumulative sieve curve of 2.0 m drop height
在2 m 高度的冲击下可以看出:(1)勒洛四面体+0.15 mm 粗粒级别产率分别比钢球和钢段介质降低3.14 和1.85 百分点;(2)中间易选级别-0.074+0.038 mm 产率分别提高5.86 和2.26 百分点;(3)细度-0.074 mm 级别产率分别提高0.4 和1.41 百分点;(4)过粉碎级别-0.01 mm 产率分别降低4.52 和2.64 百分点。
勒洛四面体各项破碎产率都明显优于传统介质,这是由于(1)同等质量的介质勒洛四面体拥有更大的接触面积,同时拥有点、线、面接触三种方式;(2)重心位于几何中心磨损均匀使用寿命长,由于尖端是圆形或平坦的面,因此减少了工作中的碰撞而导致的加速磨损的过程;(3)堆密度比其他形状介质更大,减少了工作空间,介质边缘形状可根据实际矿石力学性质改变成锐边、圆边、棱边等。
将图4~图8 中拟合的表达式列入表3,根据铜矿破碎的粒度分布函数,利用最小平方差法对不同冲击速度下铜矿粒度分布进行拟合,拟合曲线如图5~图8 所示,可见利用威布尔分布函数可以很好地拟合铜矿破碎后粒度分布规律,拟合后的分布函数以及相关系数见表3,拟合方程的拟合系数范围为0.96~0.99,证实利用威布尔分布函数来描述铜矿冲击破碎的粒度分布规律是可靠、可行的,也说明冲击速度对铜矿冲击破碎粒度分布规律影响很小。
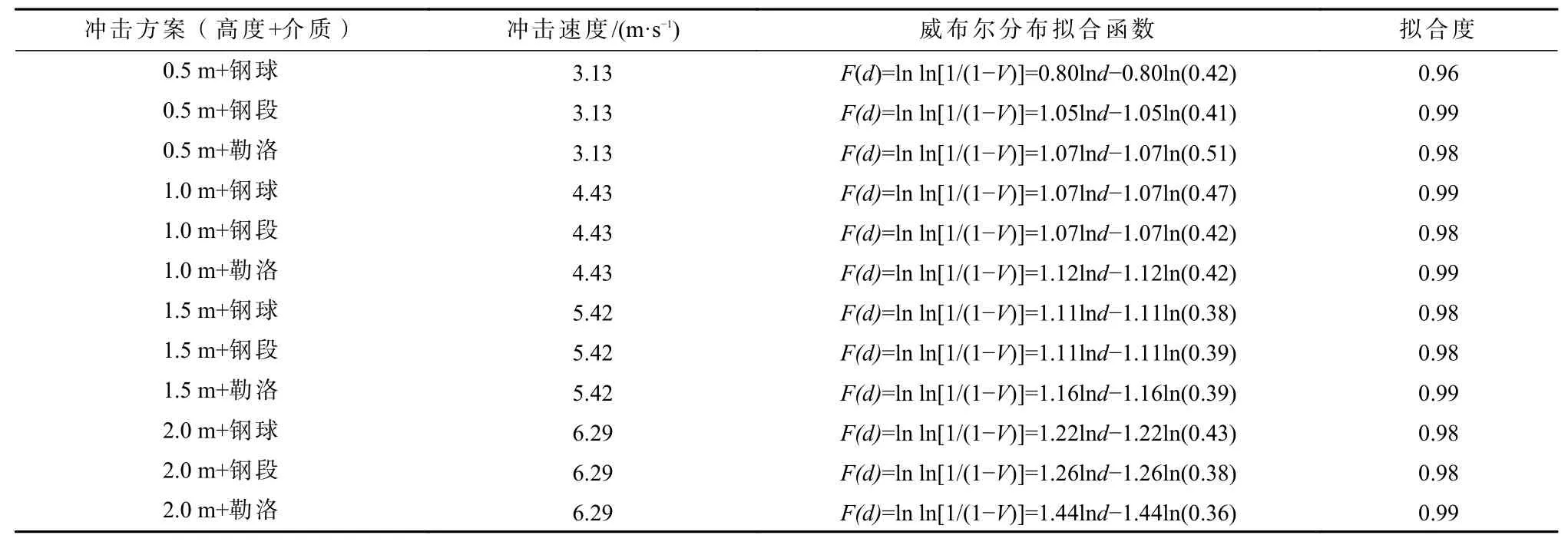
表3 铜矿质量累积分布拟合函数Table 3 Copper ore mass cumulative distribution fitting function
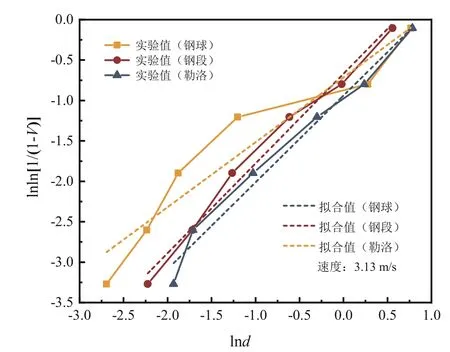
图5 0.5 m 铜矿冲击破碎粒度分布Fig. 5 Impact crushing particle size distribution of 0.5 m copper mine
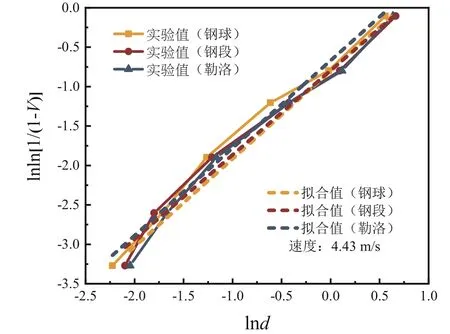
图6 1.0 m 铜矿冲击破碎粒度分布Fig. 6 Impact crushing particle size distribution of 1.0 m copper mine
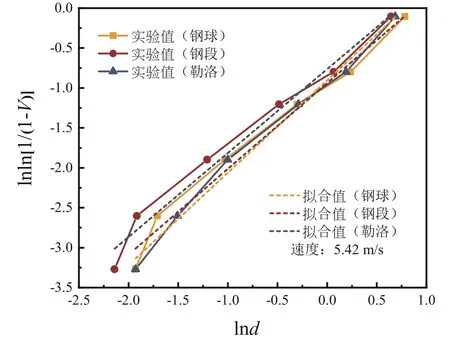
图7 1.5 m 铜矿冲击破碎粒度分布Fig. 7 Impact crushing particle size distribution of 1.5 m copper mine
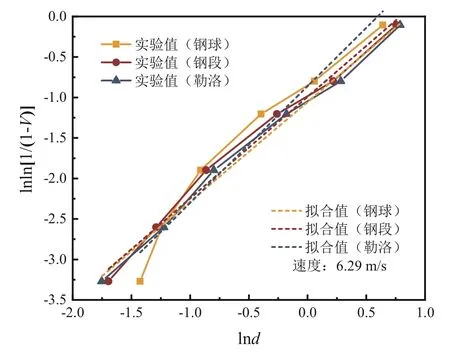
图8 2.0 m 铜矿冲击破碎粒度分布Fig. 8 Particle size distribution of impact crushing in 2.0 m copper ore
根据表3 的威布尔分布拟合函数的铜矿破碎特性指数与速度的关系可得出,铜矿破碎特性指数随冲击速度增大呈上升趋势,而结合表征破碎程度参数随冲击速度变化规律,从图9 和表2 中可见冲击速度越大破碎后铜矿的各级别产率越合理,勒洛四面体介质的铜矿破碎特性指数增加幅度最为明显,其冲击破碎效果最好。
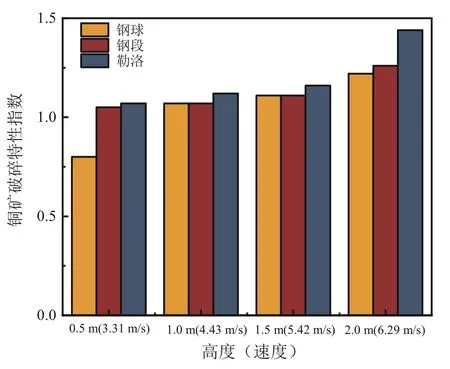
图9 各高度下拟合铜矿破碎特性指数Fig. 9 Fitted copper ore crushing characteristic index at each height
4 结论
为探究等质量的勒洛四面体介质形状比传统介质形状对球磨机矿层冲击破碎效果,通过模拟落重进行冲击实验并使用威布尔模型对破碎后的产品粒度进行拟合,得出主要结论:
(1)冲击实验结果表明,勒洛四面体介质对矿层冲击破碎后的产品粒度组成随着冲击高度的增加而变得均匀。
(2)2 m 高度时,相比钢球和钢段,勒洛四面体+0.15 mm 粗粒级别产率分别降低3.14 和1.85 百分点;中间易选级别-0.074+0.038 mm 产率分别提高5.86 和2.26 百分点;细度-0.074 mm 级别产率分别提高0.40 和1.41 百分点;过粉碎级别-0.01 mm 产率分别降低4.52 和2.64 百分点。
(3)冲击破碎产品粒度组成吻合威布尔分布规律,说明冲击速度对铜矿石冲击破碎粒度分布规律影响较小;勒洛四面体介质的铜矿破碎特性指数增加幅度最为明显,说明其冲击破碎效果最好。
