轻量化高精度三维眼动追踪系统

赵志林， 赵歆波， 闫琳婕， 梁子麟

(西北工业大学 计算机学院， 西安 710129)

0 引言

眼动跟踪是近年发展起来的一种获取人眼注视点和追踪视线的高新技术，作为一种新型的视觉感知与认知研究的基础方法，眼动跟踪已成为当前心理学、计算机科学、人机交互等学科的研究热点，并在多个场景中应用广泛。在航空航天方面，它可用于飞行员培训与操作支持，太空任务中的操作帮助以及人机界面设计优化。同时，在医疗保健领域，该技术可监测患者的目光移动，为医生提供更深入的认知和神经疾病之间关系的了解。而在交通安全领域，它有助于监控疲劳驾驶和分心驾驶，以提升驾驶员的注意力和行车安全。此外，该技术还在虚拟现实和增强现实应用中表现出色，能够实时追踪用户的视线，提升互动体验。除此之外，眼动跟踪技术在人机界面优化、心理研究、市场营销、教育和培训等多个领域都拥有很高的创新应用潜力。

目前眼动跟踪普遍采用基于模型的三维方法来实现。Lai等[1]通过提前对两个相机和两个光源进行位置标定，计算出三维视线。Mikka等[2]在左右眼各配备一个眼部相机和六个红外灯，建立了以瞳孔和角膜中心为主的三维眼球模型，同时使用卡尔曼滤波对注视点进行估算和降噪，实现了精度在0.62°左右的三维视线估计。Sun等[3]使用四个提前标定的红外光源来捕捉左右眼的反射亮斑，并以眼球中心到四个亮斑的方向向量作为特征向量拟合视线方向，平均误差为0.6°。上述方法均需要对相机和光源位置进行复杂的配准，计算量较大同时设备繁重。

为减少设备重量，Swirski[4]提出了一种仅使用单目相机的三维眼球重建方法。不过，该方法只是对仿真环境中合成的人眼图像进行了模型评估，从眼部相机到场景相机的映射精度的真实性能并没有被量化。为了解决映射带来的误差，Wang[5]尝试通过假设眼球的生理参数来建模角膜折射，但由于眼球的生理参数因人而异，导致性能不稳定。Xia[6]在头部坐标系中准确估计眼球中心和相机光学中心，并建立了两个方向特征之间的映射关系来计算视觉轴的方向。通过准确估计参数，降低映射关系的复杂性，实现了更好的拟合性能。另一方面，为了计算注视深度信息，Mikka在获得双眼视线方向后，计算其在场景图像中的交叉点深度信息，实验结果表明，其在60 cm以内具有良好的测量效果。针对设备滑移带来的误差，Larsson等[7]尝试使用惯性测量单元(Inertial Measurement Unit，IMU)来对头戴式设备的滑移进行补偿，处理后误差下降了40%左右，验证了IMU补偿的有效性。

综上所述，配准复杂、计算量大、设备繁重是现有基于多摄像机多红外灯的三维眼动跟踪系统难以克服的瓶颈，难以在要求轻量化和高精度的航空航天领域获得应用。

为此，本文提出并实现了一种单相机单光源轻量化高精度三维眼动追踪系统。针对Wang等现有方法眼球参数估计难的问题，采用单目相机和单红外光源获取瞳孔轮廓，通过逆投影法向量求交方法精确计算眼球中心；为了弥补Swirski方法标定映射精度低的缺陷，首选采用平滑尾随的方式进行快速标定；其次，为了解决Mikka方法有效测量深度较短的缺陷，通过结合双眼视线方向和场景图像交叉以获取注视深度信息，有效测量深度提升了20 cm；最后，提出了一种IMU滑移补偿算法对设备滑移误差进行校正，提高了系统的可靠性和鲁棒性。

本系统的实现不仅呈现了一种轻量化的三维眼动追踪解决方案，同时也极大地提高了系统在测量深度范围与准确性方面的表现。这些特点使得本系统在航空航天、医疗保健、交通安全、虚拟现实与增强现实和人机界面优化等多领域拥有广泛的应用前景。

1 方法介绍

1.1 系统组成

本文硬件系统组成如图1所示，系统由一个场景相机、两组眼部相机、红外灯以及一个IMU组成。场景相机(1920×1080，75 fps)位于框架中心位置，使用23 mm焦距广角镜头模仿人眼正常视场。红外灯的波长为910 mm，在此光照环境下，瞳孔与虹膜之间的对比度更明显且更易区分。为避免被试者视线遮挡，两个红外眼部相机(640×480，75 fps)位于眼球斜下方位置。

图1 系统硬件组成

系统整体流程如图2 所示。系统首先对眼部图像进行瞳孔特征提取，根据瞳孔时序序列计算出眼球中心和实时瞳孔中心，再由眼球中心和瞳孔之间的位置关系估算出三维视线。通过标定映射获得注视点坐标并且计算左右眼视线方向与场景图像的交点获得注视深度，最后对设备滑移造成的误差进行校正。

图2 系统流程

1.2 单相机单光源三维眼动追踪技术

本文基于文献[4]构建了眼球模型，其中眼球是一个近似球体，瞳孔是一个与眼球表面相切的三维圆，视线方向为从眼球中心指向瞳孔中心的三维方向矢量。

1.2.1 瞳孔轮廓提取

对Haar-like模板[8]优化改进以实现眼部区域快速定位。如图3所示，黑白相间的中心环绕特征设计与左右分布的特征模板，提升了瞳孔和虹膜区分度，进而实现快速定位；且有效减少了眼睑和睫毛遮挡带来的干扰。

图3 Haar-like 特征模板对瞳孔快速定位

对定位后的眼部图像进行边缘检测，根据瞳孔在眼眶中的位置特性、瞳孔椭圆长短轴之比的形状特性与瞳孔与虹膜相比的灰度特性，对候选边缘进行评估和筛选。

对筛选后的最佳边缘进行最小二乘拟合[9]，如式(1)所示。

F(A，B，C，D，E)=

(1)

式中，(xi，yi)表示边缘上的已知像素点，A、B、C、D、E为标准瞳孔椭圆的五个参数。

分别对参数求偏导计算极值点，得瞳孔椭圆参数，如式(2)所示，

(2)

1.2.2 计算眼球中心

令上节得到的瞳孔椭圆时序序列为Ii，0≤i≤300。拟定瞳孔半径r，对序列Ii进行三维圆拟合，利用单目视觉位姿测量算法[10]得到椭圆逆投影，进而求得三维圆序列，如图4所示。

图4 瞳孔逆投影求交计算眼球中心

其中，r与瞳孔三维圆的位置相关，与其法向量ni无关，且每组法向量总会相交于一点，即三维眼球中心c。

计算迭代优化后的法向量交点，在法向量集合LN中随机抽取M条直线集合LM拟合一个眼球中心的投影cm，如式(3)所示。

统计与cm相距指定范围内的直线数量，从中取M条直线并计算其交点。选取阈值距离内直线数量最多的一组，并将组内符合阈值条件的直线再次计算交点。当拟合结果稳定时，该组直线拟合的交点即为眼球中心c。

1.2.3 求解瞳孔中心

图5 计算眼球半径

(3)

图6 求解实时瞳孔中心

(5)

式中，L和d的长度分别由式(6)和式(7)求得。

(6)

(7)

最终计算出眼球中心到瞳孔中心的三维矢量即为视线方向：

(8)

1.2.4 标定与映射

通过平滑尾随的一点式标定，按照均匀分布的收集路线移动视线收集足够多的标定点，并对数据进行九参数映射多项式回归，其注视点与视线方向角的映射关系如公式(9)和公式(10)所示：

(9)

(10)

式中，xi和yi为标定点坐标，αi和βi分别为视线方向nreal-time转换而来俯仰角和偏航角，由于眼球绕Z轴旋转，故不考虑滚转角。

1.3 计算注视深度

由于对三维视线进行二维注视点映射缺乏注视深度信息，本文设计了一种双目视线空间求交法来计算注视深度。

图7 注视点-眼球模型

求解双目的注视距离δL与δR，如式(11)与式(12)所示。

(11)

(12)

将δL与δR代入式(13)计算左右眼注视点的中点，即为场景坐标系下三维注视点的坐标VPoG(x，y，z)。

(13)

式中，CL与CR分别为左右眼眼球中心的坐标，注视点坐标z分量即为注视深度信息。

1.4 滑移补偿

使用头戴式测量设备时，设备滑动会对后续的眼动测量结果产生较大误差，为此本文设计了一种IMU 滑移补偿算法来进行误差进行校正。

当发生滑动时，系统记录的运动信号是真实注视点运动和设备滑动的运动组合。水平和垂直方向滑移补偿后的结果可表示为：

ex(n)=sx(n)-px(n)

(14)

ey(n)=sy(n)-py(n)

(15)

式中，e(n)代表当前真实注视点坐标，s(n)为系统得到的注视点坐标，p(n)表示设备滑动导致的偏移量。

使用惯性测量单元(IMU)记录滑移数据来补偿px(n)和py(n)，其中IMU包括了加速度计、陀螺仪和磁力计三种传感器[12]。将三种传感器信号结合成包含每个欧拉角方向的三维信号(φ，θ，ψ)[13]，并依据式(16)计算注视点坐标系中的α，β，如图8 所示。

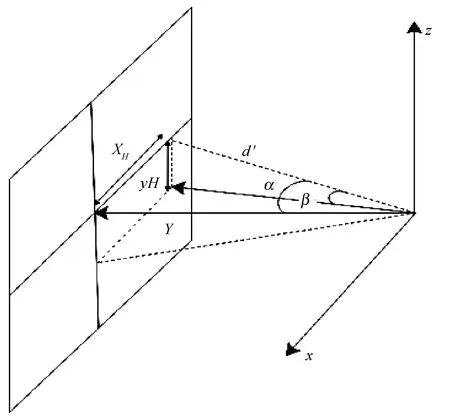
图8 映射后的欧拉角示意图

(16)

计算滑动偏移量p(n)，见公式(17)

(17)

式中，(xmax，ymax)为场景相机的分辨率，(αmax，βmax)为水平和垂直方向上的最大角度视图。

当眼动仪的眼部摄像机检测到眼部图像发生变化时，即说明发生滑动，系统开始对此后的注视点数据进行校正。在式(14)、式(15)中减去估计的滑动运动px(n)和py(n)，得到真实的眼动数据e(n)，减小滑动带来的误差。

2 实验过程与结果

2.1 实验设计

本文设置6组实验，分别从注视点精度、注视深度可用性、滑移补偿效能三个方面对本系统进行验证。

表1展示了四种三维眼动追踪系统的硬件对比。表1表明在使用相同材质框架的情况下，本文使用的单相机单光源设备重量仅为85克，与Tobii最新款头戴式眼动仪glass3 pro保持在同一水平，相比于其他眼动跟踪设备更为轻量化。

表1 不同三维眼动追踪系统硬件对比

图9 实验测试点分布

(18)

为验证注视深度计算方法的可用性，在灯光明亮的房间里，被试者注视预设定的六个测量点，每个点凝视2 s以上，在每个注视点中随机抽取100帧的数据。设置六种观察距离(分别在0.4 m、 0.6 m、 0.8 m、 1 m、 1.2 m、 3 m处)，这些不同的注视距离用来测试校准距离之外的设备性能，注视点采用圆点进行视觉刺激且每个注视点的数据分开采样，以Mikka的深度测量方法作为对照。

为验证滑移补偿算法，模拟使用过程中发生的滑动。在距刺激网格屏幕1.5 m处，要求被试者注视网格中的标记，网格大小(水平和垂直)为105 cm × 73 cm(从1.5 m的距离看，相当于40 cm × 28 cm)。被试者双手握住眼动仪在水平和垂直四个方向上进行模拟滑动，以约1 Hz的速率移动眼动仪1～2 cm。并与Larsson提出的滑移补偿效果进行对比。

为了评估眼动追踪数据中补偿眼镜滑移运动的效果，计算了四种不同情况下注视稳定目标时的标准差：

(1)正常使用眼动仪注视测量点后，不进行滑移运动补偿；

(2)正常使用眼动仪注视测量点后，进行滑移运动补偿；

(3)当注视测量点时刻意模拟使用过程中发生的滑动，并且不进行滑移运动补偿；

(4)当注视测量点时刻意模拟使用过程中发生的滑动，并且进行了滑移运动补偿。

实验数据的计算如式(19)所示

(19)

2.2 实验结果

注视点精度实验，选用目前最新且精度较高的文献[3]中Sun设计的双目多红外灯系统，来与本系统作对比。图10 中(a)和(b)分别展示了本文的算法与Sun算法的注视点分布，其中红点表示测试基准点，绿点表示该算法得到的注视点。通过计算得到两种算法误差对比，如表2 所示，表明本文EyeSecret系统平均误差为0.582°，相比于Sun算法的0.613°提升了0.031°。

表2 本文与Sun方法注视点误差对比

图10 两种方法的实验注视点分布

表3给出了不同注视距离的情况下的精度对比结果，可以看出本文方法在0.8 m测量范围内的精确度明显优于Mikka算法，而随着距离的增大，三维视线的汇聚角度逐步缩小，两种方法的精度误差也随之增大，但对这些距离处的二维投影映射的影响非常小，二维注视点精度依然能够保持在较高水平。

表3 实际距离与估计的凝视距离(平均、中值和标准差)

滑移前后使用补偿算法的系统精准度对比如表4 所示。当测试人员被要求不刻意移动设备，并且进行滑移运动补偿后，注视点的标准偏差从0.7°降至0.6°左右；当设备发生滑移后，水平方向的标准差从2.39°降至1.13°，垂直方向的标准差从1.99°降至0.85°。相比Larsson算法在补偿前后分别在水平方向提升了0.09和0.65、垂直方向提升了0.06和0.48。

表4 滑移前后使用补偿算法的系统精准度对比(标准差)

实验表明，本系统相比Sun方案减少了一个眼部相机、三个红外灯和大部分连接线材，重量仅为其1/4左右，更符合轻量化的要求；由于不存在多相机与红外灯之间配准误差的问题，本系统拥有更高的注视精准度；当注视范围在0.8米以内时，系统能够精确地测量注视深度信息；此外，使用本文设计的滑移补偿算法，可以将设备滑移带来的误差减少53%。

3 结论

本文设计了一种轻量化、高精度、具备深度信息测量和滑移补偿能力的EyeSecret三维眼动追踪系统。该系统使用单目相机和单红外光源对眼球进行建模，计算出双眼视线方向和注视点信息，并通过左右眼视线交叉得到注视点深度，同时使用IMU滑移补偿算法对设备滑移误差进行校正。实验表明，本文的系统在仅重85 g的条件下注视精准度能够达到0.58°，能够有效测量80 cm内的注视点深度距离，且可以使设备滑移带来的误差减小53%，从而满足了轻量化和高精度的要求。该系统的设计和实现，可以为航空航天等特殊领域的三维眼动跟踪方向的研究提供一种全新的解决方案，因而具有广阔的应用前景。