解三角形中的最值或范围问题

李鸿媛

⦿ 哈尔滨师范大学教师教育学院

1 与边有关的最值或范围问题

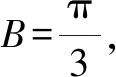
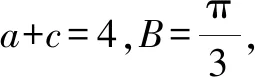
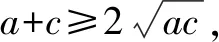
评析：本题利用已知条件结合余弦定理,借助基本不等式求三角形边的取值范围[1],渗透了逻辑推理、数学运算等数学核心素养.

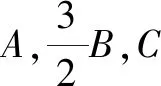
评析：本题考查了学生对等差数列的概念、三角形内角和定理、三角形面积公式、余弦定理等的掌握情况.解题的关键是将余弦定理与不等式相结合,进而求出三角形一边的最值.

2 与角有关的最值或范围问题

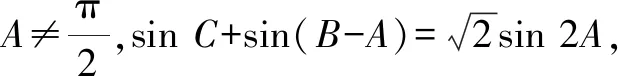
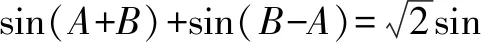
评析：解法一利用三角形内角和定理、两角和与差的正弦公式、正弦定理与三角函数的性质等知识,对学生的推理能力、运算能力和直观想象能力进行了考查.

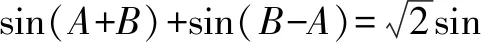
评析：解法二考查了三角形内角和定理、两角和与差的正弦公式、正弦定理、余弦定理、基本不等式等知识.这种解题方法需要学生灵活运用两个正数的和与积的关系,充分体现学生的数学运算能力和数据分析能力.

3 与周长有关的最值或范围问题

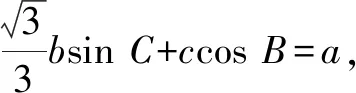
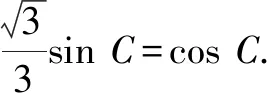
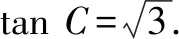
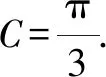
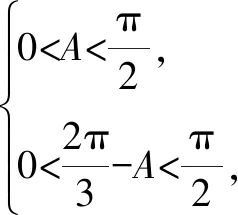
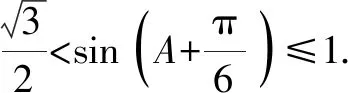
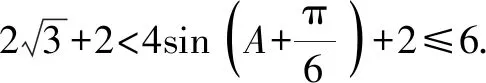
因此△ABC周长的最大值为6.

评析：这道题解题的关键是利用正弦定理将边化为角,转化为求三角函数的最值问题[2],考查了逻辑推理和数学运算等核心素养.

4 与面积有关的最值或范围问题

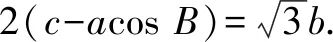
(1)求角A;

(2)若a=2,求△ABC面积的取值范围.

解法一：(1)略.

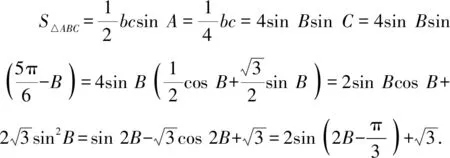
解法二：(1)略.

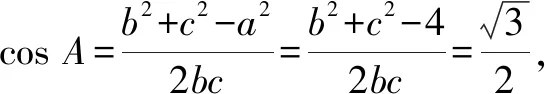
数学这门学科需要学生具备较强的逻辑推理能力、运算能力、直观想象能力等.针对解三角形最值或范围问题,学生需要熟练掌握三角形的面积公式、同角三角函数的基本关系、正弦定理、余弦定理、基本不等式等知识,并能够进行综合运用.