基于教学做合一理念的数学项目式学习活动设计
——以“解救希帕索斯”为例
2023-12-16王锦熠浙江省湖州市湖州师范学院313000
王锦熠(浙江省湖州市湖州师范学院 313000)
为落实立德树人根本任务,《义务教育数学课程标准(2022年版)》(以下简称《新课标》)提出数学教育应促进学生逐步形成适应终身发展需要的核心素养。课程目标转向以综合性与实践性为导向的育人方式变革,以学生为核心、以真实问题为驱动的数学项目化学习成为落实核心素养的有效路径。运用陶行知教学做合一理念指导教学,有助于确保数学项目式学习的综合性与实践性,保证项目式学习活动设计与实施的有效性,从而逐步培养学生的核心素养。
一、 教学做合一理念与项目式学习
1.教学做合一理念概述
教学做合一理念是陶行知在对生活教育研究的基础上提出的教育教学方法,富有生活法和教学法两层意蕴。
首先,教学做合一理念是对生活法的说明。立足生活教育理论,陶行知对教、学、做的内涵及其关系进行了阐述:“在生活中,对事说是做,对己之长进说是学,对人之影响说是教。教学做是一体三面的关系,有个公共的中心,这个中心就是‘事’,就是实际生活。”基于“以事为中心”观点,陶行知进一步强调,教学内容只有以生活为核心,教育才能满足学生实际生活需要,拿“活的东西去教活的学生”,才能发展学生的“活本领”。
其次,教学做合一理念是对教学法的界定。立足“行以求知知更行”教学观,陶行知对教、学、做如何“合一”作出进一步阐释:“教的方法根据学的方法;学的方法根据做的方法。事怎么做就怎么学,怎么学就怎么教。”基于“以事定学”“为学而教”观点,陶行知对“如何做”展开进一步论述:“做”即“在劳力上劳心”,具有行动、思想和新价值的产生三个基本特征,其最高境界是创造。
通过对“教”“学”“做”及“合一”内涵及关系的充分认识,可归纳出陶行知先生“以事定学、为学而教、学以致事”的教学基本主张,如图1所示。

图1 教学做合一理念图示
2.基于教学做合一理念构建数学项目式学习活动设计路径
数学项目式学习以解决现实问题为重点,促进学生通过调用数学及其他学科知识、能力、品质等创造性解决问题,最终实现学习迁移与素养习得。遵循教学做合一理念“以事定学、为学而教、学以致事”基本主张设计项目式学习活动,能确保数学项目式学习的真实性与有效性。因此,研究确定如图2所示的数学项目式学习活动设计路径,并以“解救希帕索斯”项目为例,对“以事定学、为学而教、学以致事”深入分析。

图2 基于教学做合一理念的数学项目式学习活动设计路径
二、 以事定学: 确定项目式学习主题与目标
确定主题与目标是进行项目式学习活动设计的起点,主题明确了项目式学习的场域,目标则规定了项目式学习的方向。二者相互契合、彼此影响,共同成为项目式学习活动设计的导航。
1.项目主题的确定
教学做合一理念指出,教学内容应以实际生活中的“事”为中心。真实性成为项目式主题的重要特征,真实性强调项目解决思路、相关知识技能可以迁移并解决现实生活问题。教师可从新课标的内容要求、教材内容特征、学生的生活经验、相关社会热点等维度入手,创设真实性的项目主题。
例如,新课标提出在教学中应关注数学文化的重要价值,结合信息时代对学生信息搜集、分析与筛选能力的培养。学生在七年级学习了无理数,并在八年级学习了勾股定理,但未充分认识无理数在数学发展中的价值,也尚未建立无理数与勾股定理的关联,故可着眼于第一次数学危机的起源:毕达哥拉斯学派与希帕索斯关于无理数存在合理性的争执上,依此设计兼具真实性与数学性的项目主题“解救希帕索斯”。
2.项目目标的确定
“以事为先”的数学项目式学习关注学生在真实情境下运用数学及其他学科知识与方法分析和解决问题。基于对项目式学习功能性的考察,可从跨学科视角出发,在项目式学习过程中着眼于“四基”“三会”,从情境与问题、知识与技能、思维与表达、交流与反思四个维度设计数学项目式学习目标。
例如,“解救希帕索斯”项目旨在通过创设为希帕索斯辩护的情境,让学生运用数学及跨学科知识发现由无理数引起的纷争,进而通过数学推理充分论证无理数存在的合理性,理解无理数在数学中的重要价值。可设计如表1所示的“解救希帕索斯”项目学习目标。

表1 “解救希帕索斯”项目学习目标设计
三、 为学而教: 驱动性问题引领项目式学习活动
教学做合一理念强调“为学而教”,即“怎么学就怎么教”。以“学”为视角出发,项目式学习关注学生在驱动性问题的引领下,综合运用数学及其他学科知识进行建模、论证和解释,通过真实情境下的问题解决实现核心素养发展。驱动性问题作为贯穿项目式学习的引擎和脉络,其质量直接决定着项目式学习的成败。因此,项目式学习活动设计的关键在于高质量驱动性问题的设计。基于教学做合一理念“为事而学,为学而教”的基本主张,可明确驱动性问题的设计原则,并依此设计“解救希帕索斯”项目的驱动性问题,最终实现以驱动性问题有效引领数学项目式学习活动。
1.驱动性问题的设计原则
数学项目式学习中高质量驱动性问题的设计应考虑项目的来龙去脉,学生的主动参与,具体而言,高质量驱动性问题的设计应遵循如下原则:
一是目标指向性。驱动性问题设计的本质在于促进学生“为事而学”,高质量驱动性问题的设计应指向项目式学习目标的达成。例如,通过对“解救希帕索斯”项目目标的分析,可设计该项目核心驱动问题:“如果你是希帕索斯的支持者,你会如何就‘无理数存在的合理性’,说服毕达哥拉斯学派接受‘万物皆数’之外还有数的存在,从而解救希帕索斯?”
二是情境真实性。驱动性问题的真实与否将直接决定学生参与项目式学习活动的意愿。情境真实性并非要求驱动性问题的每个要素都必须“真实”,而是要让学生看到知识与世界的某种联系。例如,“解救希帕索斯”项目的核心驱动问题借助数学文化让学生感悟无理数与数学发展的联系,通过“模拟辩论——无理数存在的合理性”让学生感悟数学与生活的联系。
三是相互关联性。驱动性问题之间的关联度决定着项目式学习活动的难度。因此,旨在“为学而教”的驱动性问题设计应遵循真实性问题解决的思路和学生的最近发展区。例如,从学生视角对“解救希帕索斯”项目的核心驱动问题进行分析,可确定该问题解决基本思路:分析希帕索斯的死亡原因——明确为希帕索斯辩护的思路——有理有据地论证辩护思路——解救希帕索斯,从而设计如下项目环节驱动性问题:“希帕索斯是谁? 其死亡的深层原因是什么?”“如果你是希帕索斯观点的支持者,你为希帕索斯的辩护思路是什么?”“如何有理有据地展开你的辩护内容,从而解救希帕索斯?”
四是探究持续性。项目式学习关注学生对驱动性问题的持久、深度理解,旨在通过学生的深度参与发展核心素养。因此,项目式学习不是“一锤子买卖”,驱动性问题应为学生提供持续且深度探究的机会。例如,解救希帕索斯并非项目的终点,可设计更为开放的驱动性问题,助推学生对“解救希帕索斯”项目深度思考:“作为数学的‘先知者’,在解救希帕索斯之后,你认为毕达哥拉斯学派可以进一步研究什么内容,从而推动数学的发展?”
2.驱动性问题的具体设计
基于对教学做合一理念“为事而学、为学而教”教学主张的分析,结合驱动性问题的设计原则,可进行“解救希帕索斯”项目驱动性问题的整体设计,见图3。
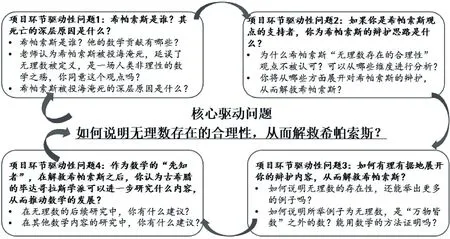
图3 “解救希帕索斯”项目驱动性问题设计
3.以驱动性问题引领项目式学习
驱动性问题引领的课堂教学往往需要经历驱动性问题的发现、提出、分析与解决、整体回顾4个主要环节。在项目式学习中,师生可借助“驱动性问题板”来呈现和组织驱动性问题。表2通过“解救希帕索斯”项目驱动性问题的具体实施,实现以驱动性问题引领数学项目式学习活动。

表2 “解救希帕索斯”项目驱动性问题的课堂实施
四、 学以致事: 项目成果展示与学习评价设计
“学以致事”是教学做合一理念的核心,也是数学项目式学习活动有效性的保证。“学以致事”在内容形式上主要关注以下两方面:一方面,学生能否在活动中将数学问题解决过程转化为具体的项目成果;另一方面,学生能否有效梳理项目学习过程中所运用的数学知识与技能,并借助多元学习评价,与同伴交流并反思学习过程中遇到的挑战。因此,在数学项目式学习活动设计中可规划项目成果展示与学习评价设计两大环节,用以检验项目式学习设计与实施的有效性。
1.项目成果展示
项目成果是数学项目式学习的结晶,也是学生通过数学问题解决过程实现思维进阶的外在表现。项目成果展示的方式依具体项目内容与目标而定。
例如,在“解救希帕索斯”项目中,基于对项目学习思路与重点的考察,可通过撰写论文《论无理数的有理性》,启发学生系统梳理“希帕索斯的发现及其证明、无理数与其他数学内容之间的关联”等问题,实现对学生专家思维的培养。同时,可基于数学文化在数学教学中的浸润目标,将解救希帕索斯的过程以“话剧+数学”的形式呈现,在对项目起始情境回应的同时,激发学生数学学习热情。
2.学习评价设计
学习评价是数学项目式学习活动设计与实施有效性的检验,“教-学-评”一致性则是学习评价设计的指南。因此,遵循项目式学习目标与多元评价理念,可设计如表3所示的评价量表供学生自评、他评及教师评价,打分时按从低到高的1~3分对每一栏进行赋分。
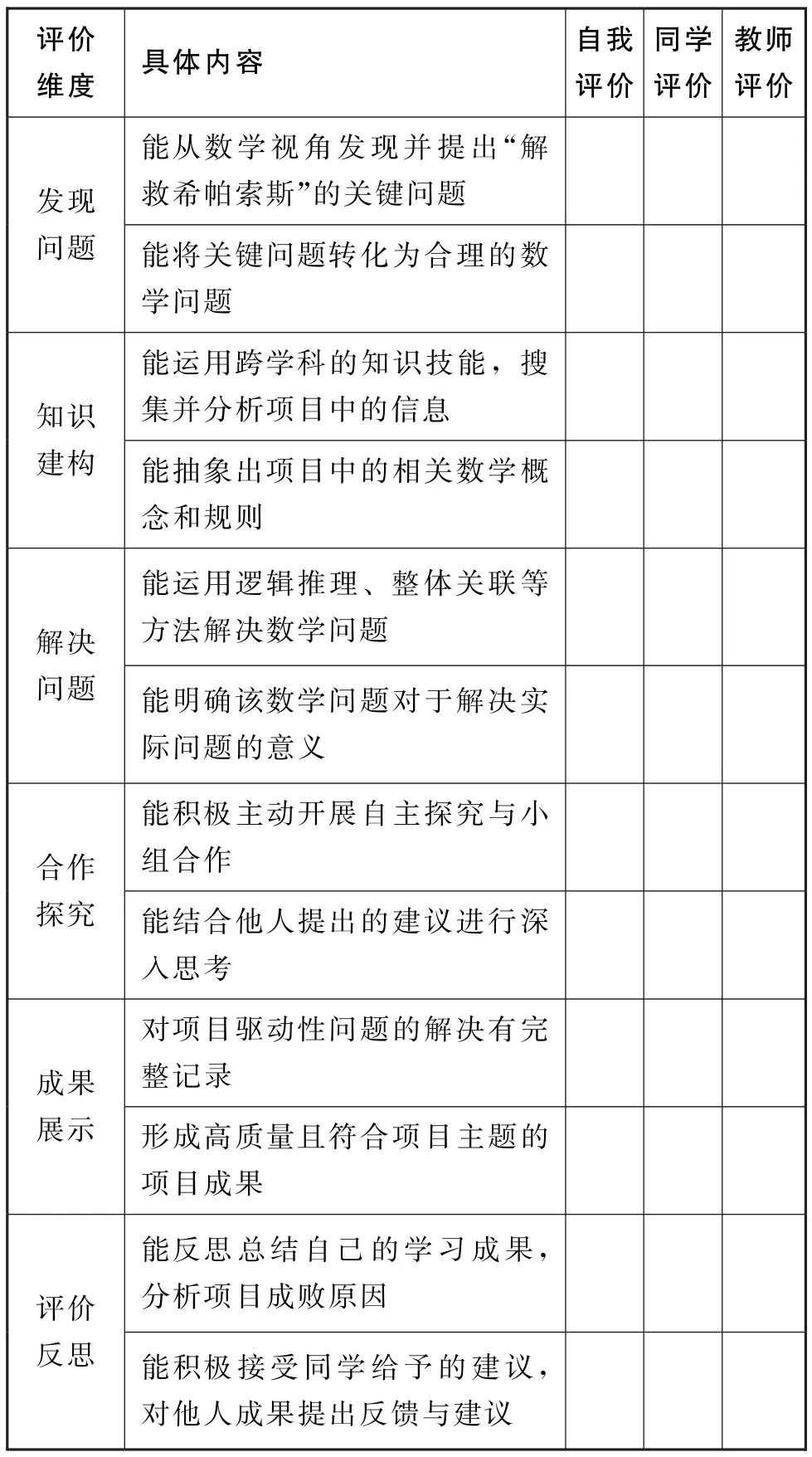
表3 “解救希帕索斯”项目学习评价设计
