基于FP-tree 和MapReduce 的集合相似度自连接算法
2023-12-15冯禹洪吴坤汉黄志鸿冯洋洲陈欢欢白鉴聪
冯禹洪 吴坤汉 黄志鸿 冯洋洲 陈欢欢 白鉴聪 明 仲
1 (深圳大学计算机与软件学院 广东深圳 518060)
2 (中国科学技术大学计算机科学与技术学院 合肥 230027)(yuhongf@szu.edu.cn)
集合相似度自连接是大数据分析的重要操作,它是从一个集合集中找出相似度大于给定阈值的集合对,有着广泛的应用,如协同过滤[1]、检测近似重复的网页[2]、社交网络分析[3]等.其中,度量2 个集合的相似度可根据应用选择合适的度量函数,如Jaccard函数.
集合相似度自连接需要度量集合集中所有集合对的相似度,时间复杂度为O(kn2), 其中n为集合集的大小,k为任意2 个集合相似度的平均计算时间.当集合规模较大时,如2019 年第3 季度知名社交网络平台Facebook 的月活跃用户人数为24.5 亿[4],每个用户都有好友集合.Facebook 用户好友集合的自连接计算中n=2.45×109,这样的大规模数据集给时间复杂度高的集合相似度自连接计算带来挑战.基于要处理的数据是静态数据还是动态数据(流数据),现有集合相似度自连接计算方法可以划分为2 类:批处理式计算和流处理式计算.
首先,批处理式集合相似度自连接计算要处理的是静态数据,运行过程中没有新增数据.现有提高运行效率的批处理式集合相似度自连接计算方法可以划分为2 类:近似计算方法和基于过滤-验证框架的准确计算方法.近似计算方法通过设计合适的集合相似度快速估算方法来加速计算,如基于位置敏感哈希函数的MSJL[5]、基于局部敏感过滤的LSFJoin[6]、基于高维数据速写和索引的CPSJoin[7]等,但因估算降低了精度导致不能找出所有相似度超过阈值的集合对.本文将关注准确计算方法.
基于过滤-验证框架的准确计算方法包括allpair[8], PPJoin[2], MPJoin[9], AdaptJoin[10], GroupJoin[11]等,其计算采用先过滤后验证的2 阶段计算方法.第1 阶段使用合适的过滤策略将检测发现的相似度低于阈值的集合对删除,获得较小的候选集;第2 阶段基于规模减小后的候选集验证并输出相似度大于给定阈值的集合对,提高了效率.有效的过滤策略是提高这类算法的重要支撑技术,常用策略包含长度过滤[12]、前缀过滤[8]、位置过滤[2]等.最近提出的位图过滤[13]采用哈希函数创建表达集合特征为固定长度的位图,然 后通过位操作推断集合对相似的上界,实现相对使用其他策略最高达4.50 倍的性能提升.
同时,并行分布式计算方法通过将大规模计算或数据划分为一系列较小的分片,每个分片被分发到不同计算节点上并行运行以提高计算效率.根据计算节点的体系结构,并行分布式集合相似度自连接计算可以划分为基于GPU 的计算和基于CPU 的计算.基于GPU 的系列算法有效提升了集合相似度连接的计算性能[14],但是,基于GPU 的实现需要对硬件有深入的了解,这往往需要编程者付出很高的学习成本.而基于CPU 的集群计算是更为普及的并行分布式计算,现有的基于CPU 的并行分布式集合相似度连接算法大部分基于MapReduce[15]框架.根据处理过程是否将集合切分为多段,基于MapReduce 框架和过滤-验证框架的集合相似度连接算法可划分为2 大类:1)集合整体过滤与验证,这类算法包括RIDPairsPPJoin(下文简称为RP-PPJoin, 有些文献也称为VernicaJoin)[16], MGJoin[17],SSJ-2R[18]等;2)集合数据分段过滤与验证,如FS-Join[19].第1 类算法将集合切分为多段,分段过滤,然后合并验证.这类算法容易被理解,但存在同一集合多次重复验证的现象.第2 算法避免了重复验证.但当阈值较低时,这2 类算法产生的候选集规模都比较大,运行效率并不理想[20].
其次,流处理式集合相似度自连接计算处理的是动态数据,该数据指的是随时间依次产生的数据,如网络监控数据、气象测控等.其数据量随着时间增长,显著特征是数据有时间戳,能快速生成.集合流处理计算通常基于批处理计算方法,引入集合相似度时间衰减因子、采样降低数据量从而提高计算效率,如串行式计算的基于PPJoin 设计的流处理计算算法SSTR[21]、基于更新日志的递增式流处理计算算法ALJoin[22]等,分布式计算的流处理计算算法BundleJoin[23]和KNN Join[24]等.
综上所述,面向静态数据基于MapReduce 的并行分布式集合相似度自连接计算效率无论对批处理式计算还是流处理式计算都很重要,本文拟采用频繁模式树(frequent pattern tree, FP-tree)[25],通过用更紧凑的扩展前缀树结构表示数据并压缩到内存中处理,减小生成的候选集的规模,同时减少I/O 操作,降低后续计算复杂度.本文将系统地研究FP-tree 及其派生结构FP-tree*,设计针对集合相似度自连接计算更有效的FP-tree*,并设计相应的基于MapReduce 框架的并行分布式集合相似度自连接算法.本文的主要贡献有3 点:
1)提出面向集合相似度自连接的遍历效率更高的线性频繁模式树 TELP-tree(traversal efficient linear prefix tree)结构模型及基于它的集合相似度自连接算法TELP-SJ,该算法包括2 阶段过滤算法,减小树的规模和减少对树结点的遍历,降低集合对相似度计算和验证的时空复杂度;
2)设计基于TELP-tree 和MapReduce 的并行分布式集合相似度自连接算法FastTELP-SJ;
3)基于4 组真实应用数据集进行3 组性能比较实验,分别进行TELP-SJ 算法与其他基于FP-tree*的算 法,如FastTELP-SJ,TELP-SJ,FastTELP-SJ 等 和 现有其他基于 MapReduce 算法的比较,本文实验结果展现了FastTELP-SJ 算法在处理高维大规模集合相似度自连接计算时的性能优于其他算法.
1 基于FP-tree 的集合相似度自连接算法
给定集合集x={x1,x2,…,xn} , 任意xi,xj∈x,xi和xj都是集合,集合相似度度量函数sim(xi,xj) ,阈值t,x的集合相似度自连接是找出所有满足sim(xi,xj)≥t的集合对 (xi,xj).
为方便讨论,本文以Facebook 开放的大规模应用数据集Facebook applications dataset II[26]的部分数据为例,演示基于其构建的FP-tree 派生结构,面向集合相似度自连接计算存在的问题及后续算法的处理过程.示例数据如图1 的X所示,其中uid代表用户标识号,aid代表应用标识号.在示例数据的应用场景中,uid和aid可以分别被理解为集合标识号和元素标识号.对任一用户ui,其使用的应用可表示为集合A(ui) ,如A(u1)={a1,a2,a3,a4,a5}.如式(1)所示,当集合A(ui)和A(uj)的 相 似 度sim(A(ui),A(uj))用Jaccard(A(ui),A(uj)) 来 计 算 时,sim(A(u1),A(u3))=3/(5+3-3)=0.6.

Fig.1 Transpose of sample data图1 示例数据转置
FP-tree 数据结构最初用于挖掘频繁模式,为使用它来计算集合相似度自连接,我们首先要将其中集合交集大小的计算转化为基于频繁二项模式挖掘的计算.为此,转置X的行与列得到X′的 数据,X中任意2 个集合A(ui)和A(uj)的 交集大小 |A(ui)∩A(uj)|的计算就转换成X′中二项集 (ui,uj)出 现的频次fi,j[27]的计算.如X′中 二项集 (u1,u3) 出现的频次f1,3=3,示例数据中|A(u1)∩A(u3)|=|{a1,a2,a3}|=3,f1,3=|A(u1)∩A(u3)|.另外,X′中 一项集ui出 现的频次与X中的 |A(ui)|出现的频次也相等.
1.1 FP-tree 及其派生结构
FP-tree 是一种扩展前缀树结构,该树保留了所有项集的关联信息,基于FP-tree 可以递归地挖掘出所有的频繁项集[25].FP-tree 数据结构模型由2 部分组成:头表和树结构.头表由三元组表示(元素,频次,头指针),其中“头指针”指向树结构中元素相同的第1 个结点,头表中的三元组按照频次递减排序.树结构结点由六元组表示(元素,频次,计数,父结点指针,子结点指针,下一个元素相同结点的指针),其中“计数”指的是共同前缀出现频次的计数,“下一个元素相同结点的指针”用于构建索引链,把树中具有相同元素的结点链接起来.
构建FP-tree 包括构建头表H和树结构.X′中任一应用ai的 用户集合标记为U(ai),U(ai)元素按照频次降序排序的序列标记为S(ai).首先初始化头表和树结构,将数据集中所有ui及 其一项频次fi按照频次倒序加入头表中,相应头指针L(ui)初始化为空指针,即索引链为空;而树结构则初始化为元素为空的根结点.然后将X′中 任一应用ai相应的序列S(ai)插入头表和树结构中.对任一序列S(ai),假设当前始于根且与S(ai) 有 最长共同前缀的路径为P,则给共同前缀上所有结点的计数都加1,将S(ai)中不在共同前缀中的元素依序插入树中,同时结点ui链接到对应元素的索引链的末尾.基于图1 示例数据构建的FP-tree 见图2(a).为了简化图2 表示,树结点信息仅展示其中的3 项,并以三元组格式展示(元素, 频次, 计数).
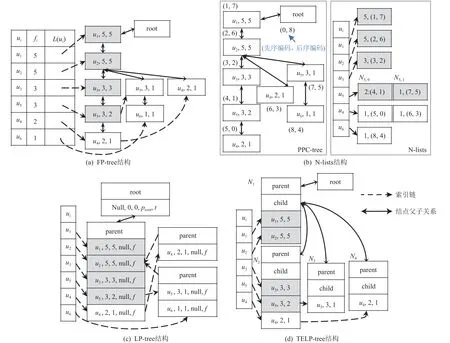
Fig.2 Construction of the FP-tree, N-lists, LP-tree, and TELP-tree over the sample data图2 基于示例数据构建的FP-tree, N-lists, LP-tree, TELP-tree
构建好FP-tree 后,简单的集合相似度自连接可以通过以下流程完成:首先根据头表结点索引链遍历树并统计所有包含这些结点元素的二项集出现频次,即相应集合交集大小;然后验证2 个集合相似度是否大于阈值;最后输出大于阈值的集合对.其中统计树二项集的频次时取二项计数值中较小者累加.例如,从头表的u3开始,索引项的第1 个树结点是(u3,3,3) ,沿分支向根结点方向遍历并统计包含u3的二项集的频次.其中 (u3,3,3;u1,5,5)的二项计数值较小者为3, (u3,3,3;u1,5,5)的 计算值为3,则f3,1暂时记为3.向上扫描完第1 个分支后,发现u3索引链只有1个 结 点,则f3,1=3.即 |A(u3)∩A(u1)|=3.而 |A(u3)|=3,|A(u1)|=5, 根据 式(1)得sim(A(u3),A(u1))=0.6,满足阈值要求,输出集合对 (u1,u3).而从u4开始,索引项的第1 个树结点是 (u4,2,1),沿分支向根结点方向遍历得到 (u4,2,1;u1,5,5)的 计算值为1,则f4,1暂时记为1.向上扫描完第1 个分支后,沿着u4索引链找到FP-tree的下一个结点 (u4,2,1) ,同理得到 (u4,2,1;u1,5,5)的计算 值为1,则f4,1=f4,1+1=2 , 即 |A(u4)∩A(u1)|=2.而A(u4)=2,A(u1)=5, 根 据 式(1)得sim(A(u4),A(u1))=0.4 <0.6 ,不输出集合对 (u1,u4).
由于基于FP-tree 的多项集频次计算或频繁多项集挖掘需要递归建树,运行期开销大.为减少这一开销,N-lists[28]采用垂直数据结构表示FP-tree 树结点,FP-tree 树结点的构建过程包含2 步:1)构建一种类似FP-tree 的树结构-前序后序编码树(pre-order postorder code tree, PPC-tree);2)构建PPC-tree 结点列表Nlist.如图2(b)所示,PPC-tree 基本与FP-tree 结构相似,不同之处在于PPC-tree 不包含索引链,同时每个树结点增加了标识结点在先序树遍历和后序树遍历中位置的先序编码和后序编码.PPC-tree 结点旁边括号中的数字,左边是先序编码,右边是后序编码.结合2个结点的先序编码、后序编码可快速判断2 个结点之间的祖先后代关系:祖先结点的先序编码大且后序编码小.为此,PPC-tree 的建树过程增加了2 次树的遍历:先序遍历和后序遍历.N-lists 是由PPC-tree中元素相同的结点按先序编码升序排序的列表,其数据结构包含头表和元素的结点列表N-list.头表结构及内容与图2(a)类似,只是头指针指向相应元素的N-list 首地址.本文的图2(b)中只画出头表中的元素信息部分.N-lists 的结点数据结构为三元组:(计数,(先序编码,后序编码)).头表元素ui的N-list 的第1个结点表项记为Ni,0, 第2 个结点表项记为Ni,1,依此类推.如u5的 第1 个结点N5,0=(2,(4,1)).特别地,头表元素的N-list 各项计数之和为元素的单项频次,例如,u5的 N-list 中2 项元组的计数之和为N5,0.计数+N5,1.计数=2+1=3=f5.
假定二项集 (ui,uj)都 是排序的二项集,ui的先序编码小于uj,则 (ui,uj)的N-list 也是按先序编码升序排序的列表,可通过将ui与uj的N-lists 按规则相交合并而成:分别取ui和uj的 N-lists 上的任意一个结点Ni,k和Nj,l,如果结点之间存在祖先后代关系,则将(Nj,l.计数,(Ni,k.先序编码,Ni,k.后序编码)) 插 入 (ui,uj)的N-list 中.例如,u3和u5对应的N-lists 相交合并可生成(u3,u5) 的N-list, 首 先u3的N-list 只 包 含1 个 结 点N3,0=(3,(3,2)),u5的 N-list 包含2 个三元组N5,0=(2,(4,1)),N5,1=(1,(7,5)).当 比 较N3,0和N5,0时 ,由 于 3 <4且2 >1,N3,0是N5,0的祖先,即它们间有祖先后代关系,则向 (u3,u5) 的N-list 中插入1 个结点N(3,5),0=(N5,0.计数,(N3,0.先序编码,N3,0.后序编码))=(2,(3,2)); 当 比 较N3,0和N5,1时 ,由于 3 <7且 2 <5,它们之间没有祖先后代关系,因此不必向 (u3,u5)的N-list 插入新的结点.同理,频次fi,j的计算可以通过对 (ui,uj)的N-list 各项计数求和得到,如f3,5=2, 即 |A(u3)∩A(u5)|=2, 而 |A(u3)|=3,|A(u5)|=3, 根 据 式(1)得sim(A(u3),A(u5))=0.5,不 满足阈值要求,不输出集合对 (u3,u5).
基于N-lists 的多项集频次计算是基于N-lists 进行交叉合并的,不需要递归建树,提升了计算性能,但在只计算二项频次时转变为2 个N-lists 的所有元素两两对比的计算,性能反而不理想.而面向大规模集合构建的FP-tree 的树结点数量多,指针结点的寻址时间长,缓存访问命中率低,降低了遍历树的效率.线性前缀树(linear prefix tree, LP-tree)[29],在FP-tree 结构的基础上将其结点的元素字段改用数组表示,存储多个元素信息,减少内存使用并加快寻址.如图2(c)所示,LP-tree 的头表结构及内容与图2 (a)完全一样,所以本文只画出头表中的元素信息部分.而结点信息改为2 项内容:一个是存储元素信息的数组,另一个是父结点.该数组每一项的数据域用五元组表示(元素, 频次, 计数, 下一个元素相同结点的指针, 分支标志).其中,“下一个元素相同结点的指针”用于构建索引链,指向下一个元素相同的项在另一个结点的数组中的位置.父结点指向其前缀最后一个元素所在的结点及其在数组的位置.其中,当一个元素没有下一个元素相同的结点时,相应指针为 N ull.分支标志为t时表示有大于等于2 个以上的序列片段的最长共同前缀止于该元素,f表示不存在分支.LPtree 结点结构合并了多个元素结点的信息,减少了FPtree 树结点数量,图2(a)中的FP-tree 有9 个结点,而图2(c)中的LP-tree 只有4 个结点.LP-tree 通过连续存储元素信息提高了计算的效率,但结点内部存在的分支、复杂的遍历流程带来运行期开销.
1.2 TELP-tree 数据结构
为进一步提高基于FP-tree*的集合相似度自连接的计算效率,我们提出了一种遍历效率更高的线性前缀树TELP-tree(traversal efficient LP-tree)的数据结构.与线性前缀树LP-tree 相似,TELP-tree 的树结点也采用线性数组存储多个元素信息以减少树结点数量,提高树的遍历效率;而不同的是,TELP-tree 树结点内部没有分支,避免结点内分支带来复杂的运行期遍历流程管理,从而减少相应的运行期开销.
定义1.TELP-tree.TELP-tree,数据结构包含头表H和树结构,头表H与FP-tree 一样结构.TELP-tree 树结点(TELP-tree node)N包含建树和遍历树所需的3项内容:父结点P、子结点C和存储元素信息的数组E,即一个包含k个元素的Ni表示为Ni={P,C,E={E1,E2,…,Ek}}.而数组元素Ej可用三元组(元素, 频次, 计数)表示.一个由c个树结点组成的TELP-tree 可以表示为 {H,N1,N2,…,Nc}.
TELP-tree 的头表与FP-tree 一样,因此,构建TELP-tree 头表与构建FP-tree 的方式是一样的.而树结点间存在差异,因此TELP-tree 树结构的构建与FPtree, LP-tree 的构建也存在差别.对任一序列S(ai),与FP-tree, LP-tree 相似,始于根结点,找到TELP-tree 中与S(ai) 有 最长共同前缀的路径P,将P相应共同前缀上结点中所有元素的计数加1,然后将这些元素从S(ai)中移去,形成S(ai)′.如果||S(ai)′||=0,对该序列的处理完成.否则,设P上最后1 个结点中与S(ai)′有最长公共前缀的后继结点为Nsucc,根据该公共前缀长度是否为0,树结点的构建和树结点插入到树结构有所不同:1)长度为0 时,构建一个新的结点,将S(ai)′中的元素依序存进其数组中,并将该结点插入树结构和链接到对应元素的索引链的末尾,这种情况与LPtree 的树结构构建是一致的;2)长度不为0 时,将Nsucc所有公共前缀上的元素计数加1.然后将S(ai)′中在 公 共前 缀 上 的 元 素 移 除, 形 成S(ai)′′,如 果||S(ai)′′||=0,对该序列的处理完成,这种情况与LPtree 的树结构构建是一致的.如果||S(ai)′′||=0,将构建一个新的结点N′, 将S(ai)′′中的元素都依序存进其数组中.同时将Nsucc中不是公共前缀的元素都移出,重构一个新的结点N′′.最后将新构建的结点N′和N′′插入树中,即Nsucc是N′和N′′的父结点,并将N'和N''分别链接到对应元素的索引链的末尾.这一步是TELPtree 与LP-tree 因为树结点结构不同带来的树结构构建的不同之处,结点内部没有分支,简化了树结点的同时也简化了树结构的构建.
基于图1 数据构建的TELP-tree 如图2(d)所示,其中 (u1,5;u2,5)是所有输入序列的公共前缀,基于构建 树 的 规 则, (u1,5)和 (u2,5)将 分 别 成 为TELP-tree 的1 个结点里的2 个数组元素.而序列(u1,5;u2,5;u3,3;u5,3;u4,2)移 去公共前缀 (u1,5;u2,5)之后的后续片段为(u3,3;u5,3;u4,2),(u1,5;u2,5;u3,3;u5,3)移 除 公 共 前 缀(u1,5;u2,5) 后是 (u3,3;u5,3), (u1,5;u2,5;u3,3)移除公共前 缀 (u1,5;u2,5) 后 是 (u3,3), (u3,3;u5,3)是(u3,3;u5,3;u4,2)的子序列,而(u5,3)和(u4,2)没有公共前缀,所以(u1,5), (u2,5), (u3,3)这3 个数组元素组成1 个结点,计数值分别是3, 2, 1,且结点内部没有分支.最终构建的TELP-tree 有5 个结点.
相 比图2(a)中9 个 结 点 的FP-tree,图2(d)中5个结点的TELP-tree 结点少4 个,结点内数组元素寻址快.相比图2(c)的4 个结点的LP-tree,TELP-tree 的结点多了1 个,但结点数组中存储的信息少,且前缀所在结点直接指向后续片段所在结点,避免了结点内部分支,简化并加速树的遍历.
1.3 TELP-SJ 算法
1.1 节描述了简单的基于FP-tree*的集合相似度自连接计算流程,但该计算过程没有采用过滤-验证框架.为进一步提高基于FP-tree*的集合相似度自连接计算效率,本节设计基于过滤-验证框架和TELPtree 的集合相似度自连接算法TELP-SJ.
TELP-SJ 使用长度过滤策略来设计其过滤算法.长度过滤策略被应用于多个集合相似度自连接算法中,如FS-Join.当集合相似度函数为Jaccard()时,长度过滤策略如定理1[19]所示.
定理1.给定2 个集合A和B,|A|<|B|, 阈值t,如果|A|<t×|B|, 那么sim(A,B)<t.
文献[19]给出定理1 的数学证明,基于定理1,2个相似的集合应有相似的大小,反之,集合大小不相似的集合对的相似度低.与集合A的相似度大于等于t的所有集合,其集合大小一定小于等于 |A|/t.因此,可提前过滤集合大小大于 |A|/t的集合.根据1.1 节和1.2 节的建树过程可知,序列的长度将影响树的深度,长度越大,深度越深,树的遍历代价就越高.为减小构建的树的规模,根据定理1,我们首先设计面向构建树的过滤算法,该算法检测、发现并删除序列中不会与其他集合形成相似度高于阈值的集合对的集合.给定至少有2 个元组的序列S(ai),在将它插入到TELP-tree 时前先应用算法1 描述的面向构建树的过滤算法对其进行预处理:从右向左扫描S(ai)中的元素,假设最右边的2 个相邻元素分别是uk和uj,如果|A(uk)|>t×|A(uj)|, 将S(ai)按照2.2 节描述的建树过程插入TELP-tree.如果 |A(uk)|<t×|A(uj)|,根据定理1,我们有sim(A(uk),A(uj))<t,即uk与uj的相似度低于阈值t.序列片段按元素频次降序排列,此时,uk对应的元组 (uk,A(uk)) 将 从序列S(ai)中删除.删除后如果|S(ai)|≤ 1,意味着ai对应原序列中所有元素相似度都低于阈值t,原序列被舍弃,否则继续如上述过程迭代处理S(ai).面向构建树的过滤算法如算法1 所示.函数getrightmost(S(ai))表 示获取S(ai)的最右边元素.
算法1.面向构建树的过滤算法.
输入:序列S(ai);
输出:过滤后序列S′(ai).
①S′(ai)←S(ai);
② while |S′(ai)|>1 do
③ (uk,A(uk))←getrightmost(S′(ai));
④S′′(ai)←S′(ai)-(uk,A(uk));
⑤ (uj,A(uj))←getrightmost(S′′(ai));
⑥ if |A(uk)|≥t×||A(uj)||
⑦ break;
⑧ else
⑨S′(ai)←S′′(ai);
⑩ end if
⑪ end while
⑫ returnS′(ai).
例如,针对图1 的示例数据,S(a5)=(u1,5;u2,5;u5,3;u6,1), 从右向左扫描S(a5), 最右边的 |A(u6)|=1,而过滤算法根据构建树(算法1),构建树的过程就是逐步插入树节点的过程 |A(u5)|=3, 1/3 <0.6,根据面向构建树的过滤算法删除元组 (u6,1), 得到S′(a5)=(u1,5;u2,5;u5,3).此时最右边的|A(u5)|=3, 而|A(u2)|=5,3/5=0.6 ,将S′(a5)插入到 TELP-tree.应用面向构建树的过滤算法构建的TELP-tree 如图3 所示,与图2(d)中没有应用该过滤算法构建的TELP-tree 相比,图3中的TELP-tree 减少了1 个树结点N4, 树的结点N3的数组元素减少了1 个,头表元素 |H|也减少了1 个,即少了u6相应的信息.
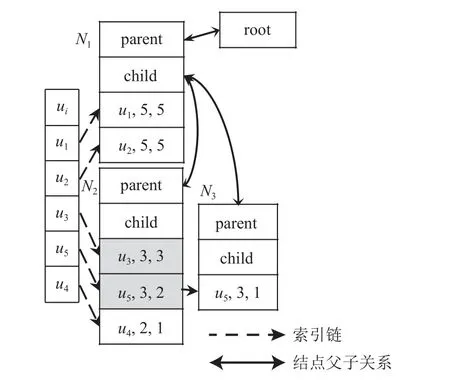
Fig.3 A TELP-tree is constructed based on filtering algorithm图3 基于过滤算法构建的TELP-tree
构建好TELP-tree 后,通过沿着头表结点索引链遍历树并统计所有以这些结点为后缀的二项集频次,根据树的特征,树结点元素频次越高越靠近根结点.树结点内数组元素按频次倒序排序.树的遍历代价跟遍历的结点数和结点内数据元素的个数有关.沿着索引链从远离根结点的树结点向着根结点的方向遍历树,统计索引链结点元素与其他元素的二项频次.同样,根据定理1,非根结点元素ui及其祖先结点元 素uj如 果 满 足 |A(ui)|<t×|A(uj)|, 可 得sim(A(ui),A(uj))<t,即这2 个元素相似度低于阈值,此时,可以停止沿着这条分支向着根结点方向统计,即过滤对应的集合对以减少遍历.面向遍历树的过滤算法见算法2,其中,Ancestor(N)表 示树中N的祖先结点;N.x中 的“.” 表示 取结点N的 相应数 据域x, 如N.E[l]表示取结点N的元素数组E的第l个元素.
算法2.面向遍历树的过滤算法.
输入:元素ui, 树结点N, 频次统计f;
输出:频次统计f.
① whileN不为根结点 do
②l←|N.E|-1;
③ whilel≥0 do
④ if|A(ui)|<t×|A(N.E[l])|
⑤ goto ⑫;
⑥ else
⑦fi,N.E[l]+=N.E[l].计数
⑧ endif
⑨ end while
⑩N←Ancestor(N);
⑪ end while
⑫ returnf.
基于面向构建树的过滤算法构建TELP-tree,按规则遍历树并计算集合相似度自连接:1)遍历头表H中所有元素ui, 并初始化f;2)通过ui的索引链,遍历其所有树结点,对每个树结点调用面向遍历树的过滤算法,并更新f;3)根据f计算出集合相似性,并输出相似性大于阈值的集合对.例如从图3 的头表的(u4,2)开 始,顺着索引项第1 个树结点N2的数组元素(u4,2,1) 开始统计包含u4的二项集的频次.如(u4,2,1;u5,3,2)的 二项计数值较小者为1,则f4,5=0+1=1.同时注意到 |A(u4)|=2, |A(u2)|=5, 2 <0.6×5,因此,针对 (u4,2,1) ,从N2向着根结点的方向遍历树时,只需要遍历N2的 元素信息数组,不需要遍历N1.因此f4,5=1, 即|A(u4)∩A(u5)|=1.而|A(u4)|=2,|A(u5)|=3,根据式(1)得sim(A(u4),A(u5))=0.25 <0.6,不输出集合对 (u4,u5).图2 和图3 中灰色框的元素表示统计包含u4的二项集频次时要遍历的元素,没有填充灰色的框的结点和数组元素表示没有遍历的点或元素.由此,针对TELP-tree,统计包含u4的二项集的频次要遍历的结点数和数组元素分别是1 和2,而在使用过滤算法的情况下,要遍历的结点数和数组元素的分别是3 和6,遍历次数大大减少,提高了遍历效率.
以上面向构建树和树遍历的2 个过滤算法同样可以使用于其他基于FP-tree*的集合相似度自连接算法.综上,TELP-SJ 的算法的伪代码见算法3.基于FP-tree 的集合相似度自连接算法FP-SJ、基于LP-tree的 LP-SJ 均与 TELP-SJ 的计算思路基本一致,不同之处在于算法3 中行⑪,即:如果是FP-SJ,则构建FPtree;如果是LP-SJ,则构建LP-tree.遍历树的一些细节有稍许区别,如Ancestor(nk)的实现和结点的定位等操作,这里不赘述.而基于N-lists 的集合相似度自连接算法PPC-SJ,则是构建PPC-tree 后,构造N-lists,然后对任意2 个N-lists 的所有元素两两对比验证完成 计 算.FP-SJ,LP-SJ, TELP-SJ,PPC-SJ 这4 种 基 于FP-tree*的集合相似度自连接算法统称为FP-tree*-SJ.
算法3.TELP-SJ 算法.
输入:数据集D={〈ui,{ai1,ai2,…,aik}〉} , 阈值t;
输出:满足阈值的集合对集合P.
①U←∅,S←∅,S′←∅,P←∅;
② for eachui,A(ui)inD
③ for eachaij∈A(ui)
④U(ai j)←U(aij)+(ui:|A(ui)|);
⑤ end for
⑥ end for
⑦ forU(ai) inU
⑧ 对U(ai)按 频次降序排序得到S(ai);
⑨ 对S(ai) 调 用算法1 得到S′(ai);
⑩ end for
⑪ 根据S′建树tree;
⑫ for eachui∈tree.H
⑬ 初始化频次f;
⑭ for eachNkinui的索引链
⑮ 对ui,Nk,f调用算法2;
⑯ end for
⑰ 根据f计算出sim(ui,uj);
⑱P←P+{(ui,uj)s.t.sim(ui,uj)>t};
⑲ end for
⑳ returnP.
2 基于MapReduce 的集合相似度自连接算法FastTELP-SJ
MapReduce 是一种高效的并行分布式集群计算框架.一个MapReduce 任务的运行主要包含2 个阶段:映射(Map)阶段和规约(Reduce)阶段.Map 阶段首先将存储在分布式文件系统HDFS 上的输入数据划分为多个分片;然后就近分发至集群多个计算节点独立并行运行函数map,处理数据并以〈Key,Value〉对的形式输出中间结果.之后中间结果按照Key值进行合并(combine)、重新分配(shuffle)、排序(sort)后再分发至1 个或多个节点进行Reduce 阶段运算,独立并行运行函数reduce进行汇总.最终各个函数reduce的结果仍以〈Key,Value〉对的方式输出并保存在HDFS 上.
第1 节设计了系列基于FP-tree 及其扩展结构的集合相似度自连接算法FP-tree*-SJ,这些算法的特征是建树后,整棵树需要保留在内存中进行计算,当集合规模增大时,树的规模增大,对内存的要求增大,树的遍历计算代价也增大.为进一步提高计算性能,本节设计基于TELP-tree 和MapReduce 的集合相似度自连接算法FastTELP-SJ.图4 展示了FastTELP-SJ 的计算过程.FastTELP-SJ 包含2 个MapReduce 任务,分别完成数据集转置、建树和集合相似度自连接的计算.1.3 节设计的2 阶段过滤算法,分别应用于任务1和任务2.
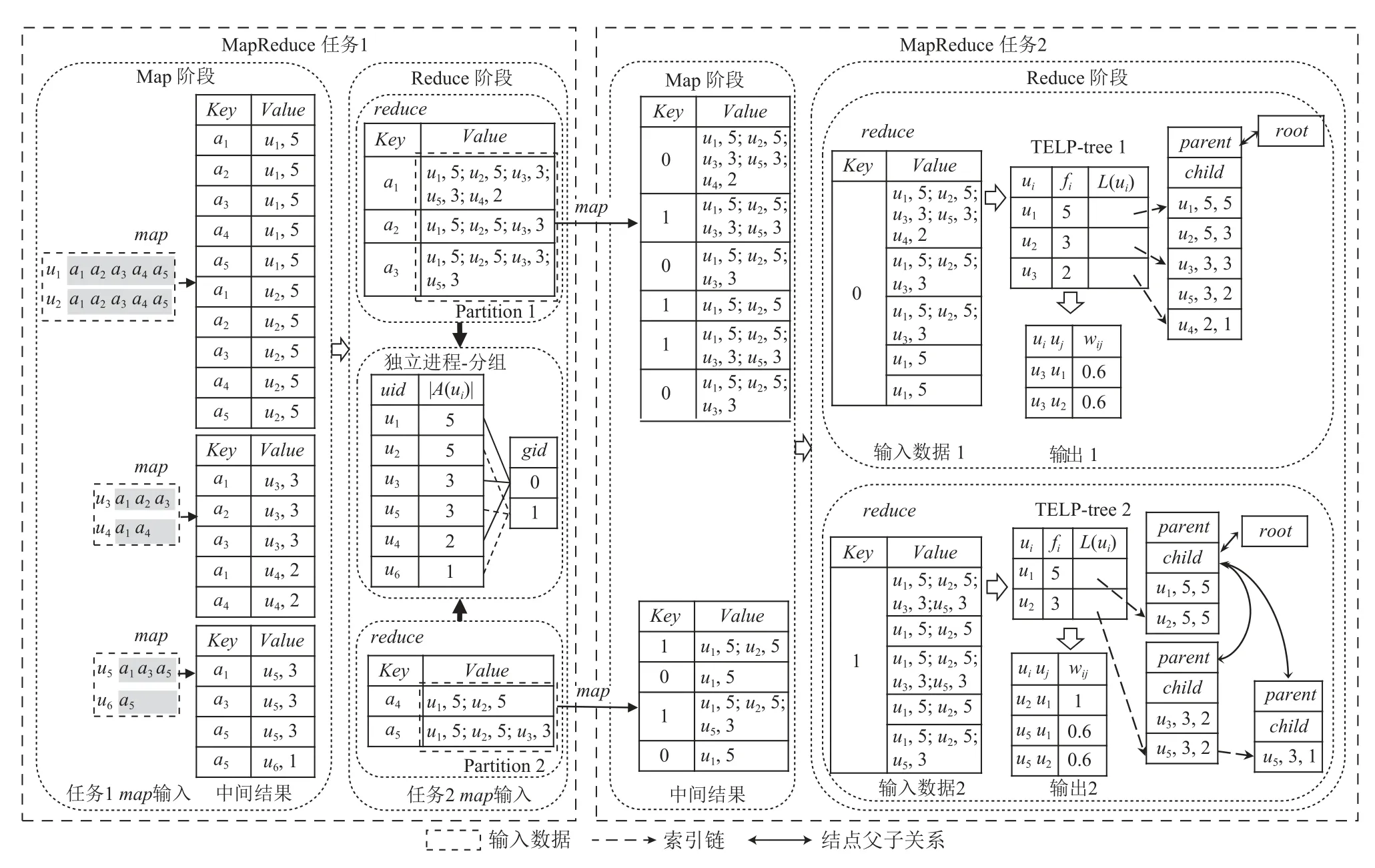
Fig.4 An illustration of the computation process of the parallel and distributed set similarity self-join of FastTELP-SJ with MapReduce图4 基于MapReduce 的并行分布式集合相似度自连接FastTELP-SJ 的计算流程示意图
2.1 转置数据集
任务1 的函数map计算每个ui的 频次 |A(ui)|、输出〈Key=aid,Value=(ui:|A(ui)|)〉对, 实现了原数据集的转置.与Key值 相同的Value将被合并和发送到同一个函数reduce.任一应用ai的Value集合标记为U(ai).函数reduce 将U(ai)元素按照频次降序排序得到序列S(ai), 调用算法1 得到S′(ai), 输出键值对〈Key=ai,Value=S′(ai)〉.例如,图4 任务1 的Reduce 阶段中S(a5)=(u1,5;u2,5;u5,3;u6,1) , 函数reduce对S(a5)应用算法1,从右向左扫描S(a5), 最右边的 |A(u6)|=1, 而 |A(u5)|=3,1/3 <0.6 ,删 除 数 据 (u6,1).同 时 |A(u2)|=5, 3/5 ≥0.6,因此输出结果〈a5,(u1,5;u2,5;u5,3)〉.任务1 的函数map与reduce的功能分别与算法3 中行②~⑥和行⑦~⑩类似,故不再赘述.
当所有reduce函数完成计算后,节点master将启动一个独立进程对元素分组,按照频次将元素排序,函数seq(ui)表 示ui的序号.假设gNum表 示组数,gi表示ui的组标识号gid.基于FP-tree 树的并行分布式计算有多种分组策略[30],这里采用基于均衡预估遍历负载的策略,即gi=seq(ui)modgNum.
2.2 构建树并计算集合相似度自连接
FastTELP-SJ 采用集合数据分段过滤与验证的设计思路,为此,任务2 首先切分序列,按分段划分数据集,然后根据数据集分片并行独立构建TELP-tree计算集合相似度自连接.其中函数map完成数据集划分工作.对任一S(ai),函数map的工作流程为:1)根据S(ai) 最 右边元素gid输出键值对〈Key=gid,Value=S(ai)〉 ;2)从右向左遍历S(ai)中 的元素uk, 如果与gid即gk相 等的键值对已输出,则将该uk从S(ai)中删去;如果S(ai)不为空,跳回1)继续迭代执行.例如,图4任务2 的函数map对序列S(a5)=(u1,5;u2,5;u5,3)将输出2 个结果:〈 1,(u1,5;u2,5)〉 和〈0,(u1,5;u2,5;u5,3)〉.任务2 中切分序列的伪代码如算法4 所示.
算法4.序列切分算法.
输入:已排序序列S(ai) , 元素分组gid;
输出:划分结果R=〈{gid,S〉}.
①R←∅,G←∅;
② while|S(ai)|>0
③(uik,|A(uik)|)←getrightmost(S(ai));
④ifgik∈G
⑤R←R∪{〈gik,S(ai)〉};
⑥G←G∪{gik};
⑦ end if
⑧S(ai)←S(ai)-(uik,|A(uik)|);
⑨ end while
⑩ returnR.
所有Key即gid相同的序列片段将被分配给同一个节点的函数reduce.因为集合相似度自连接仅需要计算单项频次和二项频次,结合面向MapReduce 计算而设计的精简FP-tree(reduced FP-tree)[29]的结构特征,函数reduce在构建TELP-tree 时,仅为gid与Key值相同的元素构建头表和索引链,减少内存空间并减少建树时间,相应的TELP-tree 称为精简TELP-tree.除此之外,树的构建过程与1.2 节相同.
构建好精简TELP-tree 后,通过对头表结点索引链应用面向遍历树的过滤规则遍历树,并统计所有以这些结点为后缀的二项集出现频次.其中树遍历过程与1.3 节描述的相同,而二项集频次统计仅对gid与reduce的Key值相同的结点进行统计.任务2 的函数reduce与算法4 的行⑪~⑳类似,故不再赘述.
综上,FastTELP-SJ 算法的计算流程示例见图4.其他FP-tree*-SJ 的MapReduce 计算可采用类似的设计,相应地,基于MapReduce 的FP-tree*-SJ 算法被命名为FastFP-tree*-SJ.
3 性能评估
基于FP-tree*的算法通过将数据压缩在内存中进行计算,减少I/O 操作,减小候选集,提高验证两两集合相似度是否大于阈值的运行效率.但这些算法也增加了动态构建树等运行期开销,同时,整棵树需被保留在内存中进行计算,对内存需求比较大.我们将从运行时间、内存占用率、磁盘使用量这3 类指标通过3 组比较实验评估FastTELP-SJ 算法的性能:1)TELP-SJ 算法与基于其他FP-tree*-SJ 算法的比较;2)FastTELP-SJ 算法与TELP-SJ 算法的比较;3)FastTELPSJ 与现有经典算法的比较.
Apache Hadoop[31]和 Apache Spark[32]是2 个最知名和最广泛使用的MapReduce 编程模型的开源实现.两者最大的区别是:Apache Hadoop 的中间计算结果保存在Apache Hadoop 分布式文件系统中,而Apache Spark 可将中间数据结果缓存在内存中.因此,对多次数据依赖的迭代算法、多数据依赖的计算任务,使用Apache Spark 可以减少I/O 从而提高运行效率.从第2 节的描述可见,集合相似度自连接计算不包含多次数据依赖的迭代计算.另外,还有些特定面向多核或众核优化的MapReduce 实现,如Phoenix[33], Mars[34]等.考虑到现有经典算法都是基于Apache Hadoop 实现,因此,本文的对比实验首先在Apache Hadoop 上复现经典算法,然后实现本文设计的算法.
实验使用一个包含17 个曙光TC4600 刀片节点搭建的Apache Hadoop 集群,其中1 个作为主节点,其他作为从节点.每个刀片都有2 个10 核的Intel®Xeon®E5-2 680 v2 2.8 GHz 的处理器、2 个1 TB 的磁盘、64 GB 的内存和1 Gbps 的以太网.刀片上安装CentOS 6.5 操 作 系 统, OpenJDK 1.8.0 和 Apache Hadoop 2.7.1.相关Apache Hadoop 参数配置见表1,其他均采用缺省配置.

Table 1 Apache Hadoop Parameter Configuration表1 Apache Hadoop 参数配置
实验数据来自4 组真实的应用数据集:Facebook应用数据集 II(简记为facebook)[35]、匈牙利在线新闻门户点击流数据集kosarak[36]、2015 年Enron 电子邮件数据集Enron[37]和交通事故数据集accidents[38].我们将从各组数据集中提取一定量的数据分别进行实验,相应数据子集命名为数据集名称后加提取的数量,如从facebook 数据集中提取10 万条数据,记为facebook10w.4 组数据集为各取近30 万条数据组成的子集,其相应数据特征总结在表2 中,其中,子集x′={x′1,x′2,…,x′n′}, 子集大小即 |x′|=n′为数据子集元素总数,表示数据集所有元素属性合集,X(a′i)表 示拥有属性a′i的元素,表示拥有该属性的元素的最大个数表示所有属性元素的平均个数,表示元素拥有属性的最大个数,表示元素拥有属性的平均个数,表示元素拥有属性个数的方差.每次计算都将运行3 次,采用平均运行时间、内存占用率峰值和磁盘使用量用于展示实验结果和分析.

Table 2 Characteristics of Experimental Datasets表2 实验数据集特征
3.1 TELP-SJ 与基于其他FP-tree*-SJ 的比较
本文分别实现FP-SJ, PPC-SJ, LP-SJ, TELP-SJ 这4 种基于 FP-tree 及其派生结构的集合相似度自连接算法,并将这些算法分别运行在facebook30w,kosarak30w, Enron30w, accidents30w 这4 组数据上,阈值t的取值范围为 0.6 ~0.9.基于FP-tree*-SJ 的集合相似度自连接计算没有产生中间结果,最后输出结果是一样的,因此这4 种算法的磁盘使用量没有差异.这4 组算法的区别在于树结构的差异及因此带来的建树和遍历树流程的差异,我们将比较这4 种算法的运行时间和内存占用率峰值.
1) 运行时间
根据第1 节的描述,基于FP-tree*的集合相似度计算的第1 步是转置数据集.数据子集x′转置后的数据 集x′′的 大 小 |x′′|为x′所 有 元 素 属 性 合 集 大 小 |A(x′)|,即|x′′|=|A(x′)|.FP-SJ, LP-SJ, TELP-SJ 等算法的计算复杂度即树遍历的复杂度而对PPC-SJ来说,基于构建好N-lists的集合相似度自连接计算是对任意2个N-lists的比较,其计算复杂度O(Nlists)=|x′|×|A(x′)|2.
图5 展示4 种FP-tree*-SJ 算法的运行时间随着阈值t提高的变化,我们可以看到在facebook30w,Enron30w, kosarak30w 这3 组数据集上FP-SJ, LP-SJ,TELP-SJ 的运行时间比PPC-SJ 的运行时间少很多.如表2 所示,这3 组数据的 |A(x′)|很大,说明原数据子集元素属性合集很大,即是高维大数据.该实验数据说明这3 种算法比PPC-SJ 更适合处理高维大规模集合相似度自连接计算,其中TELP-SJ 的运行时间最少.
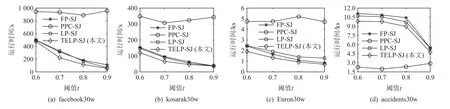
Fig.5 Relationship between FP-tree*-SJ’s running time and the threshold图5 FP-tree*-SJ 的运行时间与阈值关系
在accidents30w 数据集上PPC-SJ 的运行效率最好,其次是TELP-SJ, 最差是FP-SJ.accidents30w 的|A(x′)|=458, 而其 他3 组的都很大,所以PPC-SJ 的运行效率最好.该实验数据说明PPC-SJ 比其他3 种算法适合处理低维大规模集合相似度自连接计算.此种情况下,TELP-SJ 比FP-SJ, LP-SJ 的运行效率也要高.
表3 展示了阈值t= 0.6 时4 种FP-tree*-SJ 算法处理Enron30w 数据集时各分步的运行时间,包括建树时间、遍历树时间、总耗时.表4 展示了TELP- SJ与其他3 种算法的相对性能提升率.由表3 和表4 可见,4 种算法遍历树的时间在总耗时中占比较高,而TELP-SJ 和LP-SJ 的遍历时间少于FP-SJ 和PPC-SJ,这与第1 节的分析一致.其中,TELP-SJ 的遍历时间最少,相比于FP-SJ 和PPC-SJ 性能分别提高了32%和83%.同时,我们也看到,TELP-SJ 的建树时间和遍历树时间都比LP-SJ 少,其中建树时间性能提高了45%,遍历时间性能提高了17%,这也与第1 节的分析一致.随着阈值t的增大,因为大部分数据在第1阶段过滤中被过滤掉,候选集规模小,建树和遍历树的代价差异减小,相应地TELP-SJ 与FP-SJ 和 LP-SJ的运行时间差异减小.
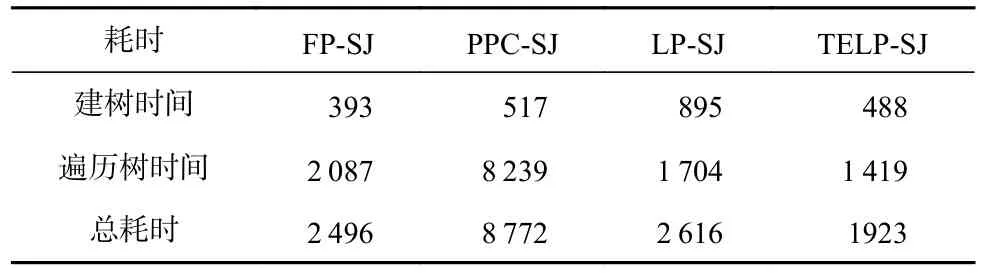
Table 3 Detailed Execution Time of Enron30w Dataset handled by FP-tree*-SJ表3 FP-tree*-SJ处理Enron30w数据集的细分运行时间 s
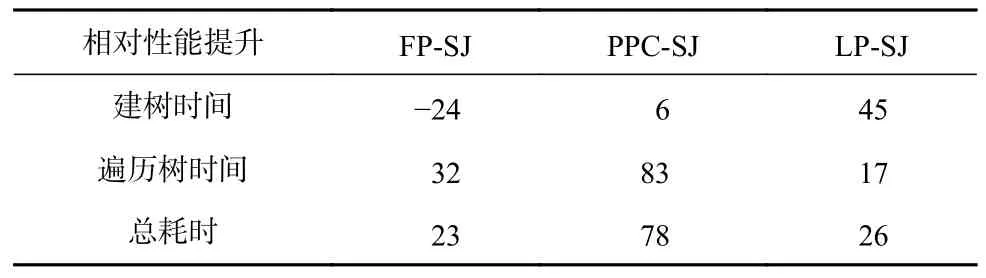
Table 4 Relative Performance Improvement of TELP-SJ Compared with Other FP-tree*-SJ表4 TELP-SJ 相对于其他FP-tree*-SJ 的性能提升 %
我们以Enron 数据集为例,阈值t=0.6,从5 万条数据起,每次每组增加5 万条,共6 组数据,分别运行4 种算法以观察它们的运行时间与数据子集大小的关系.如图6 所示,随着数据子集大小的增加,TELP-SJ 的运行时间增长速度低于另外3 种算法,可扩展性最好.

Fig.6 Relationship between FP-tree*-SJ’s running time and the size of Enron’s sub-datasets图6 FP-tree*-SJ 的运行时间与Enron 数据子集大小的关系
2) 内存占用峰值
图7 展示了阙值t= 0.6 时4 种算法运行期的内存占用率.由图7(a)(b)可见,4 种FP-tree*-SJ 算法运行期在facebook30w 和kosarak30w 数据子集上的内存占用率峰值相近,图7(c)(d)则显示在Enron30w和acciden30w 数据集上,FP-SJ 的内存占用率峰值最高,PPC-SJ 相对较低和TELP-SJ 最低,这说明TELPSJ 使用数组存储了更多的元素,具有较好的压缩比,而PPC-tree 因为使用N-lists 进行计算,不需要建立相同元素结点间的索引链,减少了内存开销.
Fig.7 Memory usage of FP-tree*-SJ (t = 0.6)图7 FP-tree*-SJ 的内存占用率(t = 0.6)
3.2 FastTELP-SJ 算法与TELP-SJ 算法的比较
本节我们以TELP-tree 为例,以FastTELP-SJ 相对TELP-SJ 的运行时间加速比及内存占用峰值评估MapReduce 对基于FP-tree*的集合相似度自连接算法的加速效果.
实验将FastTELP-SJ 和TELP-SJ 分别运行在4 个数据集的子集上,图8 描绘了2 种算法的相对加速比.其中数据子集大小始于5 万条,每次每组增加5万条,共6 组数据,阈值t分别设置为0.6 和0.9.由图8 可见,当阈值t= 0.6 时,随着数据子集大小的增加,相对加速比加大.FastTELP-SJ 相对于TELP-SJ 的相对加速比在accidents 数据子集上高达10,且在facebook 和Enron 数据子集上相对加速比的增长近似于线性.当阈值t= 0.9 时,当数据子集大小等于3 万条时,相对加速比在Enron 和accidents 数据子集上分别约为2 和7,可见采用并行分布式计算框架MapReduce 可加速基于FP-tree*的集合相似度自连接计算.
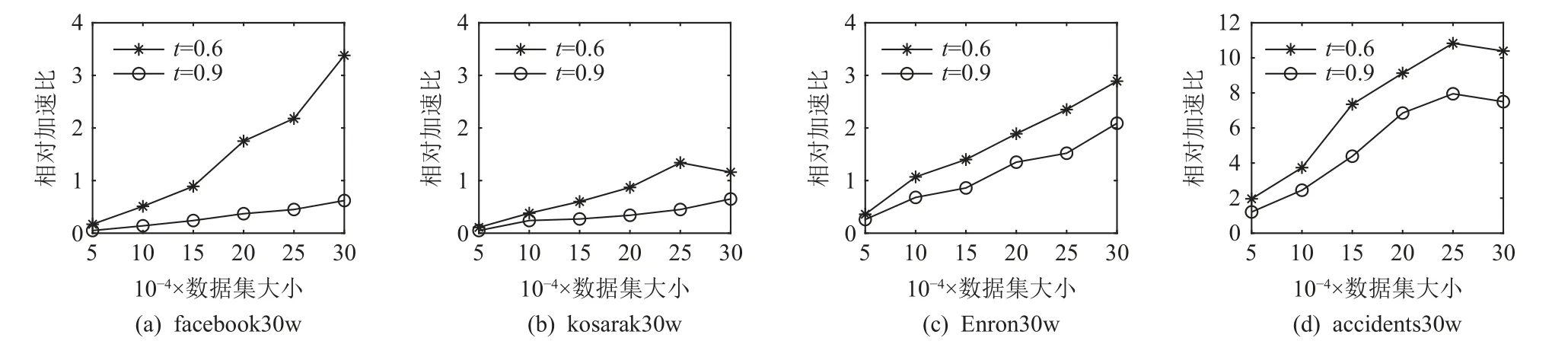
Fig.8 Relative speedup of FastTELP-SJ and TELP-SJ图8 FastTELP-SJ 与TELP-SJ 的相对加速比
当数据子集比较小时,如图8 中数据集大小小于15 万条时,FastTELP-SJ 和TELP-SJ 算法的相对加速比在facebook, kosarak, Enron 等数据子集上都小于1.同时,在所有kosarak 数据子集上的相对加速比增长都缓慢,且小于1.5.这是因为该数据集的 |A(x′)|和(|X(a′i)|)偏低,如图9 所示,转置后数据子集的规模和维度都不大,相当于小数据集.同理,当阈值t=0.9 时,大部分数据在第1 阶段过滤中被过滤掉,规模减小后的候选集变成了小数据集,因此,2 种算法的相对加速比在facebook 和kosarak 数据子集中都小于1.这是因为基于并行分布式计算框架MapReduce 的计算有额外的运行期开销,包括数据划分、合并、重新分配、排序等,当数据集比较小时,额外地运行其开销抵消甚至超过降低切分数据并行计算带来的提升.此时,TELP-SJ 比FastTELP-SJ 的运行效率高.
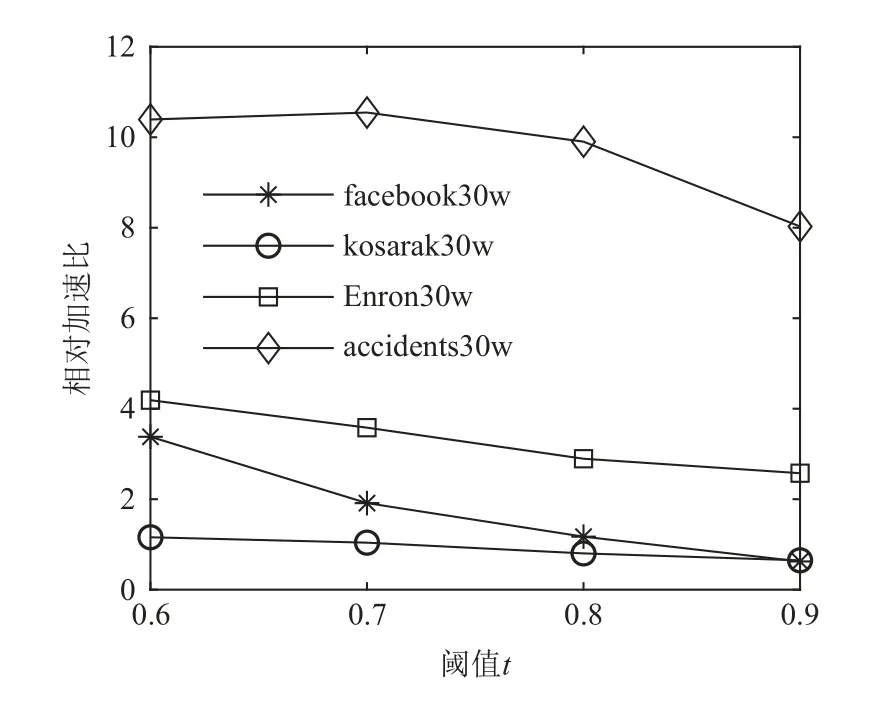
Fig.9 Relationship between relative speedups of FastTELP-SJ and TELP-SJ, and the threshold图9 FastTELP-SJ 和TELP-SJ 的相对加速比与阈值的关系
另外,图9 描绘了2 种算法的相对加速比与阈值t的关系.数据子集大小均为30 万条,阈值t设置为 0.6 ~0.9.从图9 可以看出FastTELP-SJ 和TELP-SJ的相对加速比在4 个数据集上都大于1,且随着阈值的减小,相对加速比在不断增大.这是因为在阈值减小时,第1 阶段过滤后得到的候选集规模变大,需要进行两两交集大小计算的集合对个数增多,利用并行分布式计算框架MapReduce 的FastTELP-SJ 能使用更多计算资源完成计算,因而减小计算耗时.
图10 描 绘 的 是 阙 值t=0.6时FastTELP-SJ 和TELP-SJ 在4 个数据子集上的运行期内存占用率,从图10 可见,除了在enron30w 数据子集上两者的内存占用率峰值基本相等外,在其他3 个子集上FastTELP-SJ的内存占用率峰值接近于TELP-SJ 的 1/2,即采用并行分布式计算框架MapReduce 可减少单个节点的内存负载.

Fig.10 Memory usage of FastTELP-SJ and TELP-SJ (t = 0.6)图10 FastTELP-SJ 与TELP-SJ 的内存占用率(t = 0.6)
3.3 FastTELP-SJ 与现有经典算法的比较
从3.1 节和3.2 节的实验结果可见,FastTELP-SJ在处理大规模集合相似度自连接计算时相较于基于其他FP-tree*-SJ 算法运行效率最高.RP-PPJoin 和FSJoin 是基于MapReduce 的集合相似度自连接算法的代表.另外,最近提出的位图过滤[12]在单机和GPU系统上运行均展现了它的有效性.在本节,为了更全面地评估FastTELP-SJ 的性能,本文同时设计并实现基于位图过滤策略的RP-PPJoin,记为RP-PPJoin +Bitmap.我们将通过FastTELP-SJ 与RP-PPJoin, RPPPJoin + Bitmap, FS-Join 这4 种算法的比较实验评估FastTELP-SJ 的性能.
1) 运行时间
首先将这4 种算法运行在facebookb30w, kosarak 30w, Enron30w, accidents30w 这4 组 数 据 集 上.阈 值t的取值范围为 0.6 ~0.9.图11 展示4 种算法随着阈值t的提高运行时间的变化,可以看到通过使用位图过滤,RP-PPJoin + Bitmap 在facebookb30w, kosarak30w,Enron30w 上的运行效率都得到提高.而FastTELP-SJ的运行时间在这3 个数据集上都优于其他3 种算法,尤其在阈值t<0.7 时运行时间明显降低很多.这主要是TELP-SJ 将数据压缩在内存中进行计算,减少了I/O 次数,减小了候选集和降低了计算复杂度.而此时RP-PPJoin, RP-PPJoin + Bitmap, FS-join 算法产生较大候选集,其O(kn2)的高复杂度验证计算延长了运行时间.尤其对accidents30w,当t≤0.85时,FS-Join 无法在当前计算环境中完成计算,当t<0.7时,RP-PPJoin和RP-PPJoin+Bitmap 的运行时间大幅度升高,而FastTELP-SJ 的运行时间增长不多,运行效率最高.

Fig.11 Relationship between running time of FastTELP-SJ, RP-PPJoin, RP-PPJoin+Bitmap and FS-Join, and the threshold图11 FastTELP-SJ 和RP-PPJoin, RP-PPJoin+Bitmap, FS-Join 的运行时间与阈值的关系
图12 描绘了这4 种算法的运行时间与数据子集大小的关系,以accidents 数据集为例,阈值t分别设置为0.6 和0.9.其中,0.6 代表了低阈值情况,而0.9代表了较高阈值的情况.数据子集大小始于5 万条、每次每组增加5 万条,取6 组数据,分别运行这4 种算法并观察它们的运行时间与数据子集大小的关系.如图12(a)所示,当t=0.6时,FastTELP- SJ 的运行时间低于另外3 种算法,且其运行时间随数据增长呈线性增长,可扩展性优于另外3 种算法.当t=0.9时,高阈值下各算法应用过滤策略过滤了大量相似度低于阈值的候选集合对.此时,FastTELP-SJ 的运行期开销如建树时间等导致它的总运行时间高于RPPPJoin 和RP-PPJoin + Bitmap,但仍然低于FS-Join,如图12(b)所示,这个结果也与图10 中t值较大时的结果一致.
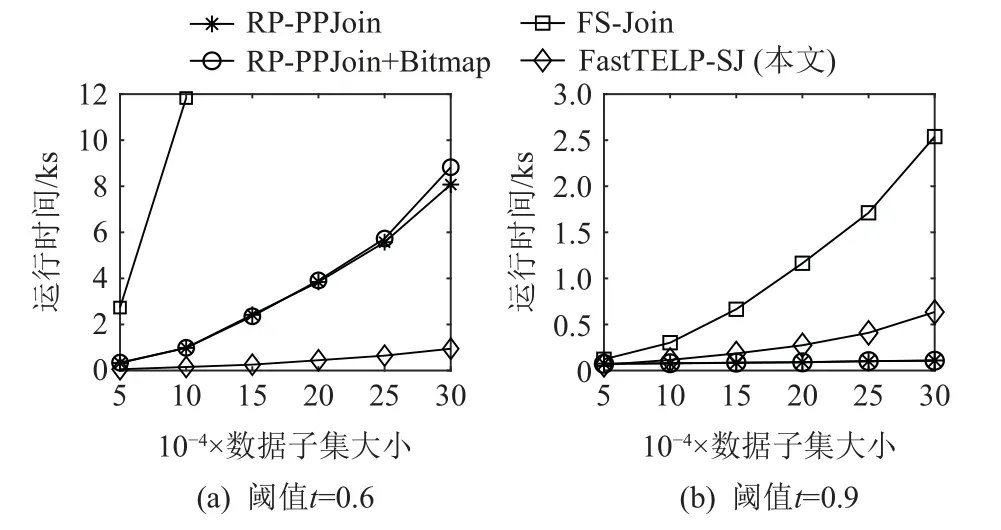
Fig.12 Relationship between running time of FastTELP-SJ,RP-PPJoin, RP-PPJoin+Bitmap and FS-Join, and the size of accidents’ sub-datasets图12 FastTELP-SJ, RP-PPJoin, RP-PPJoin + Bitmap,FS-Join 的运行时间与accidents 数据子集大小的关系
最后,我们评估这4 种算法的运行时间与集群规模的关系,其中,集群规模为集群节点个数.实验以facebook30w 数据集为例,阈值t设置为0.6,集群规模起始计算节点为2,依次增加2 个直至16 个,分别运行4 种算法并观察它们的运行时间与集群规模的关系.图13 描绘了实验结果,随着集群节点个数的增加,相比于RP-PPJoin, RP-PPJoin+Bitmap, FSJoin 和FastTELPSJ 运行时间的变化速率下降得更慢.这说明相较于其他3 种算法,FastTELP-SJ 的扩展性最好.
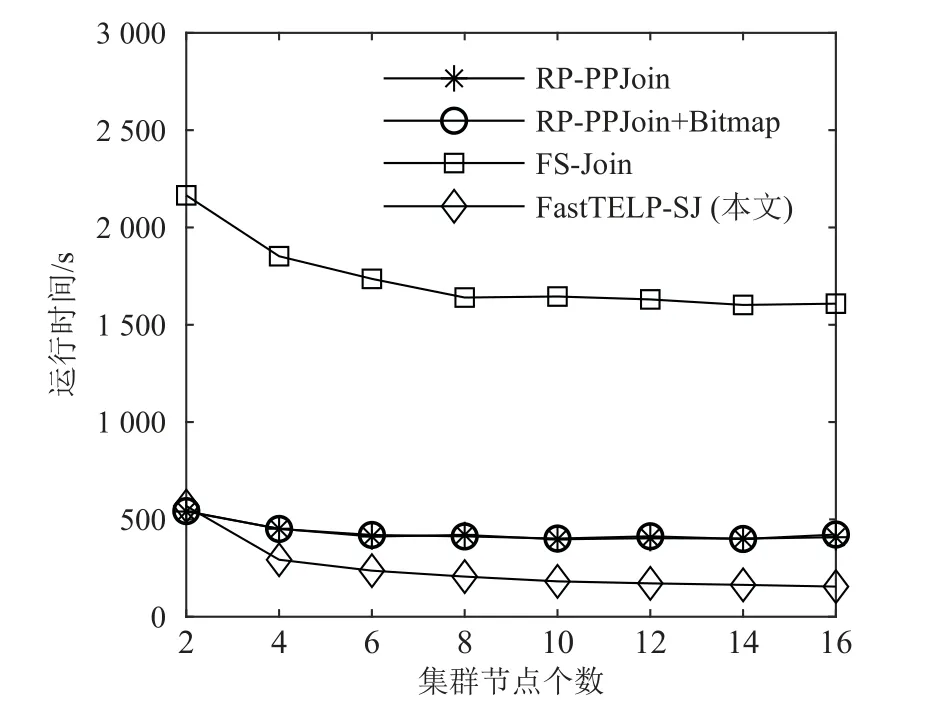
Fig.13 Relationship between running time of FastTELP-SJ,RP-PPJoin, RP-PPJoin+Bitmap and FS-Join, and the cluster’s size图13 FastTELP-SJ, RP-PPJoin, RP-PPJoin + Bitmap, FSJoin 的运行时间与集群规模的关系
2) 内存占用率
图14 描绘了4 种算法在facebookb30w, kosarak 30w, Enron30w, accidents30w 这4 组数据子集进行集合相似度自连接计算过程中的内存占用率,其中,FastTELP-SJ 在 处 理kosarak30w 和Enron30w 时 内 存占用率峰值分别是其他3 种算法的2~3 倍,因为TELP-tree 在其任务2 的函数reduce运行过程中常驻内存,这跟第1, 2 节的分析一致.但RP-PPJoin 和FSJoin 的候选集大,也有可能出现内存占用率高的情况,如图14(a)(d).同时RP-PPJoin+Bitmap 的内存占用率峰值始终最大,这是因为该算法需要为每个集合构造相应的位图并保存在内存中进行计算.
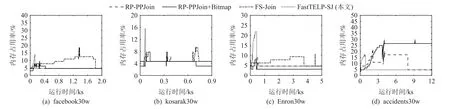
Fig.14 Memory usage of four algorithms (t = 0.6)图14 4 种算法的内存占用率(t = 0.6)
3) 磁盘使用量
图15 描绘了4 种算法在facebookb30w,kosarak 30w,Enron30w,accidents30w 这4 组数据子集上进行集合相似度自连接计算过程中的磁盘使用量.当阈值t= 0.6 时,FastTELP-SJ 在处理facebook30w,kosarak-30w,accidents30w 这3 个数据子集时的磁盘读写量最低,因为它的验证计算都在内存中完成,减少了I/O,此结论与第1, 2 节的分析和3.3.1 节运行时间相关的实验结果分析相一致.尤其是RP-PPJoin 和RP-PPJoin+Bitmap,因它们可能产生重复验证的冗余候选集,磁盘使用量最大,见图15(c)(d).而当阙值t增大时,如t=0.9时,由于过滤策略的应用,大量数据被过滤,各个算法的磁盘使用量都降低,差别也减少.
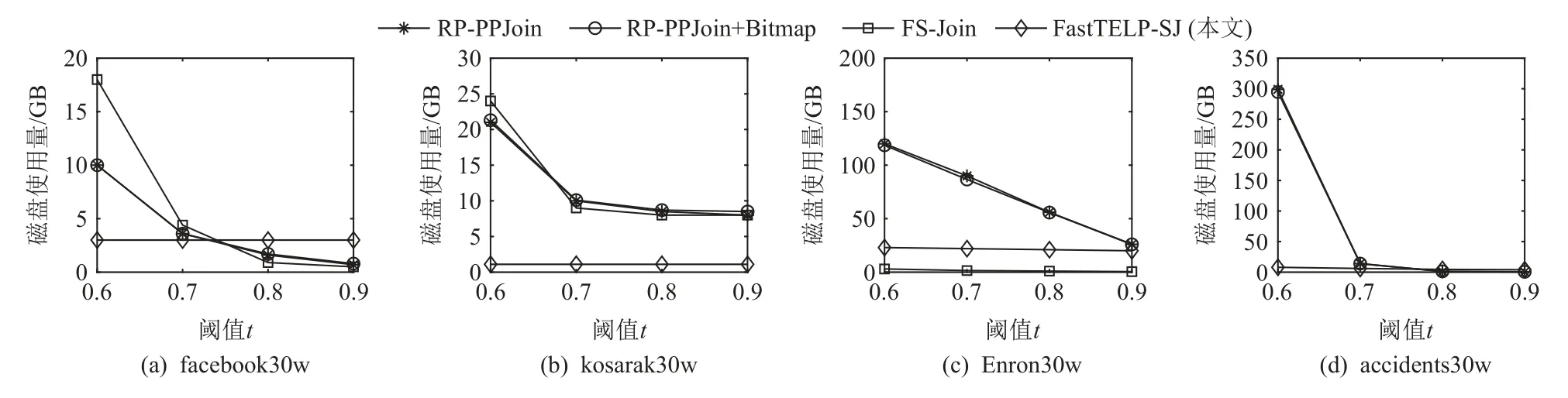
Fig.15 Disk usage amount of four algorithms图15 4 种算法的磁盘使用量
3.4 小 结
基于3.1~3.3 节的实验结果比较,当阈值t比较高时,如在我们的实验环境和数据下,t>0.8时, 4 种算法的执行性能差别不大.当阈值t比较低时,我们有4 点实验结论:
1) 高维大规模集合相似度自连接计算中TELPSJ 的运行效率最好且具有较好的可扩展性.
2) 低维大规模集合相似度自连接计算中PPCSJ 的运行效率最好.
3) 高维大规模集合相似度自连接计算中基于并行分布式计算模型MapReduce 和TELP-tree 设计的算法FastTELP-SJ 相对于TELP-SJ 有较好的加速比.
4) 大规模集合相似度自连接计算中FastTELPSJ 的运行效率优于现有基于MapReduce 的3 类算法RP-PPJoin, RP-PPJoin + Bitmap, FS-Join.
4 结束语
数据的增长、集合规模的加大给现有集合相似度自连接算法带来挑战.基于MapReduce 的并行分布式集合相似度自连接加速了计算,但当阈值较低时现有算法生成了较大规模的候选集,执行效率依然不理想.
为此,本文提出并设计采用频繁模式树及其派生结构FP-tree*加速集合相似度自连接算法:1)设计面向基于FP-tree*的集合相似度自连接算法及加速其计算的2 阶段过滤规则,减小FP-tree*的规模并提高树遍历效率;2)提出并构建面向集合相似度自连接的遍历效率更高的FP-tree 派生结构-线性频繁模式树结构TELP-tree 及基于其的算法TELP-SJ;3)设计基于MapReduce 和TELP-tree 的集合相似度自连接算法FastTELP-SJ.基于4 组真实应用数据集,通过3组比较实验从运行时间、内存占用率、磁盘使用量等方面进行对比实验来评估FastTELP-SJ 的性能,实验结果展现了FastTELP-SJ 较好运行性能和可扩展性.
FastTELP-SJ 算法将数据压缩在内存中进行计算,带来构建树和销毁树等运行期内存管理开销,同时,FastTELP-SJ 算法包含2 次MapReduce 任务,带来运行期流程管理开销.经调研,文献[39-40]设计了一种基于生命周期的内存管理框架Deca,通过自动分析用户定义的函数和数据结构,预测其生命周期.基于该预测分配和释放空间可提高系统垃圾回收效率,进而提高内存使用率.另外,文献[41-42]提出了一种面向流数据和迭代任务流程管理降低能耗的资源共享框架F3C.我们将进一步研究如何结合有效的内存管理、流程管理框架构建绿色高效的集合相似度连接计算.
作者贡献声明:冯禹洪发现问题、定义问题、提出算法思路和实验方案;吴坤汉、黄志鸿、冯洋洲负责完成算法设计、实现、性能评估;陈欢欢、白鉴聪、明仲优化算法和实验方案.所有作者共同完善国内外研究现状调研、完成论文的撰写和修改.
