基于2 阶段集成的多层网络社区发现算法
2023-12-15赵兴旺张珧溥梁吉业
赵兴旺 张珧溥 梁吉业
(山西大学计算机与信息技术学院 太原 030006)
(计算智能与中文信息处理教育部重点实验室(山西大学) 太原 030006)(zhaoxw84@163.com)
社团结构是复杂网络的一个重要特征,即同一个社区内节点之间连接紧密而不同社区间节点之间连接稀疏[1].例如,社交网络的社区代表具有相似特征的人群,蛋白质交互网络中社区代表具有相似功能的生物组织模块,万维网中不同的社区代表不同功能的网页.社区发现是复杂网络分析挖掘中的重要任务之一,对于网络拓扑结构分析、功能分析和行为预测具有重要意义,已在社会学、生物信息学、交通系统等领域得到了广泛应用[2-4].例如,在社交网络中,社区发现有助于分析个体的行为模式、信息的传播方式和网络的变化趋势[5];在生物网络中,社区发现有助于分析属于共同功能模块的蛋白质之间的相互作用[6];在交通网络中,社区发现可以通过将城市道路网络划分为多个支线网络来实现对城市交通网络的区域控制,从而缓解城市交通拥堵问题[7].
针对不同的应用领域,研究者近年来已经开展了广泛研究,并提出了系列社区发现算法,主要包括:基于划分的方法[8]、基于模块度的方法[9-10]、基于谱的方法[11]、基于动力学的方法[12]、基于标签传播的方法[13]等.已有算法大多适用于单层网络,然而现实世界中由多种类型节点及其连边关系组成的多层网络存在更为普遍[14].例如,社交网络中的个体之间可能存在不同类型的社交关系,如好友、关注、评论、转发等;在生物网络中,对于某些生物体来说,完整的蛋白质与蛋白质相互作用涉及数千种蛋白质分子之间多种不同的相互作用模式;在航空运输系统中,通过直飞航班对机场之间的连接建模,不同的商业航空公司可以被视为机场之间的不同连接模式.与单层网络相比,多层网络结构具有更加丰富的拓扑信息,有助于更为准确地探测网络中蕴含的社区结构.但是不同网络层蕴含的社区结构之间既存在一定的相关性又存在异质性,为社区发现任务带来了新的挑战.
近年来,一些学者针对多层网络的社区发现问题已经开展了有益探索,提出了相应的算法[15-16].其中,基于聚合的方法由于实现简单、具有良好的可扩展性等优点,得到了广泛关注.第1 类基于聚合的方法为网络聚合,直接将多层网络合并为单层网络,然后利用传统社区发现算法实现社区划分.该类方法虽然降低了社区发现后续研究的难度,但是在聚合过程中丢失了不同层网络结构的独特性,造成社区结果的不准确.第2 类方法为基于集成学习的方法,首先在每层网络上分别利用传统社区发现算法进行社区划分,然后基于集成学习机制将每层的社区划分融合得到最终的社区结构.这类方法在不同网络层得到基社区划分后,往往各层社区划分分别进行融合或者不同层的社区划分进行统一融合,忽视了不同层社区之间的异质性;另一方面在融合过程中忽略了不同的基社区结构和社区划分之间的重要性,难以获得准确的社区结构[17].
针对上述问题,本文提出了一种基于2 阶段集成的多层网络社区发现算法,旨在有效融合不同网络层获得的基社区划分之间的信息,提高社区发现结果的准确性和可解释性.在第1 阶段,分别以各层网络生成的基社区划分为主,并结合其他各层网络得到的基社区划分中最优的社区划分结构信息进行局部集成;在第2 阶段,首先对得到的局部社区划分及各个社区结构的重要性度量,然后进行全局加权集成得到最终的社区划分结果.
1 相关工作
1.1 基于扩展的方法
基于扩展的方法主要指将单层网络的社区发现方法直接扩展到多层网络,通常通过优化社区质量评估函数来实现.基于模块度函数优化是探测社区结构的经典方法,其核心思想是通过最大化模块度来获得社区划分结果.例如,Mucha 等人[18]将模块度扩展到了多层网络,开发了一种多层网络社区质量函数的广义框架用于检测多层网络的社区结构.该算法就是通过优化多层模块度扩展了传统的Louvain算法,从而得到一个多层模块度高的社区划分.Ma等人[19]提出了一种用于多层网络社区检测的定量函数——多层模块化密度,解决了模块度的分辨率限制问题,为社区发现算法的设计提供了理论基础,并提出了一种半监督联合非负矩阵分解的多层网络社区发现算法S2-jNMF.该算法用贪婪搜索方法提取多层网络所有层中连接良好的子图作为先验信息,然后将与多层网络相关的矩阵和先验信息联合分解为一个基矩阵和一个多系数矩阵用于社区发现.LART[20]是一种基于局部自适应随机游走的多层网络社区发现算法,它首先对每一层网络运行不同的随机游走;然后利用每层转移概率获得节点之间的不同度量;最后,采用层次聚类方法生成社区划分,最终在多层模块度的最优值对应的水平上得到社区划分结果.Laishram 等人[21]提出了一种新颖的基于采样的多层网络社区发现算法,使用来自探索成本低的层的信息来帮助探索成本高的层的信息.尽管该类方法通过对单层网络社区发现方法进行直接扩展可以对多层网络进行有效社区发现,但是存在着需要设置的参数较多、时间复杂度较高、易受噪声影响等缺点.
1.2 基于聚合的方法
为了降低社区检测的难度,基于多层网络的聚合结构进行社区发现的相关研究具有实现简单、可扩展性强的特点.这些研究主要包括基于网络聚合和基于集成学习2 类思路.
基于网络聚合的方法是将一个多层网络压缩成单个网络,然后采用单层网络的社区发现算法对其进行社区检测.最简单的策略就是对邻接矩阵进行加权,其中2 个节点之间的权值为它们在多层网络中相连的层数.Berlingerio 等人[22]对简单的加权策略进行了修改并提出了基于共同邻居数的邻接矩阵的加权策略,这种策略不再考虑2 个节点之间的直接联系,而是关注它们的邻居,共同邻居数越多则越可能在同一个社区.Zhu 等人[23]进一步考虑了每层网络的重要性,将单层网络之间的相关性与单层网络的重要性密切联系起来,若某一单层网络与其他的单层网络之间的相关性更大,则表明其重要性更强.同时判断2 个节点之间是否存在路径来衡量节点相似度,然后利用单层网络重要性和节点相似度构造统一矩阵,最后再用单层网络社区发现算法得到最终的社区划分结果.基于网络聚合方法在聚合过程中丢失了不同层网络结构的独特性,造成社区结果的不准确.
基于集成学习的方法首先利用传统算法对多层网络的各个层进行社区发现,然后基于集成学习机制将各层得到的社区划分结果进行融合得到最终的社区划分[17].Tang 等人[24]提出了主模块化最大化方法,首先通过模块化最大化从多层网络的每个层中提取结构特征,然后对这些特征进行跨层次分析,采用PCA 技术找到低维嵌入,使从所有层中提取的特征彼此高度相关,最后通过k-means 聚类算法找到社区划分.Berlingerio 等人[25]提出了一种基于频繁模式挖掘的多层网络的社区发现算法,能够从单层社区成员中提取频繁的封闭项集来提取多层社区.首先用单层社区发现算法获得每层网络上的社区,然后用频繁封闭项集算法将至少在最少数量的层上属于同一社区的节点分配到同一社区.Tagarelli 等人[17]提出了一种新的基于模块化优化的集成的多层社区发现算法,此方法在寻找共识社区结构时,不仅捕获了节点的原型社区成员,而且能够保存多层网络的拓扑信息,在获得共识解的过程中将多层网络的拓扑上界和拓扑下界作为搜索空间,共识函数也是通过基于模块化优化的方法,同时考虑了社区内和社区间的连通性.这类方法在得到不同层的社区划分后,往往各层社区划分分别进行融合或者不同层的社区划分进行统一融合.由于每一层网络中节点之间的交互方式以及社区结构的不同,进行简单集成容易忽视不同层社区之间的异质性;而且在融合过程中忽略了不同的基社区结构和社区划分之间的重要性,难以获得准确的社区结果.
2 基于集成的多层网络社区发现算法
本节首先对基于集成学习的多层网络社区发现问题进行了描述,接着对本文提出的基于2 阶段集成的多层网络社区发现算法进行了介绍.
2.1 问题描述
一个多层网络可以定义为
其 中G={Gα|α ∈{1,2,…,L}}表 示L层 网 络 构 成 的 集合,Gα=(Vα,Eα) 为 多层网络中的第 α 层,Vα⊆V={v1,v2,…,vN},Vα表示第 α层的节点集,V为多层网络的所有节点的集合,Eα⊆Vα×Vα表 示第 α层内节点之间连接的边集; A表示任意2 个不同层的节点之间的连接,可以表示为
即Eα中 的元素表示层内顶点间连接,Eαβ表示层间顶点间的连接.本文主要讨论的对象为所有层共享相同节点集的多层网络,即在给定的多层网络GL=(G,A) 中,对于每一层Gα=(Vα,Eα)∈G都 有Vα=V(V={v1,v2,…,vN}), 但是每一层内的边集不同,即Gα=(V,Eα).另外,对于层间连接
即所有层的节点是对齐的.如图1 为一个多层网络示意图,由3 层网络组成,每层均包括6 个节点,每层内的连边表示节点间的一种关系,层间的虚线表示不同层的节点是对齐的.
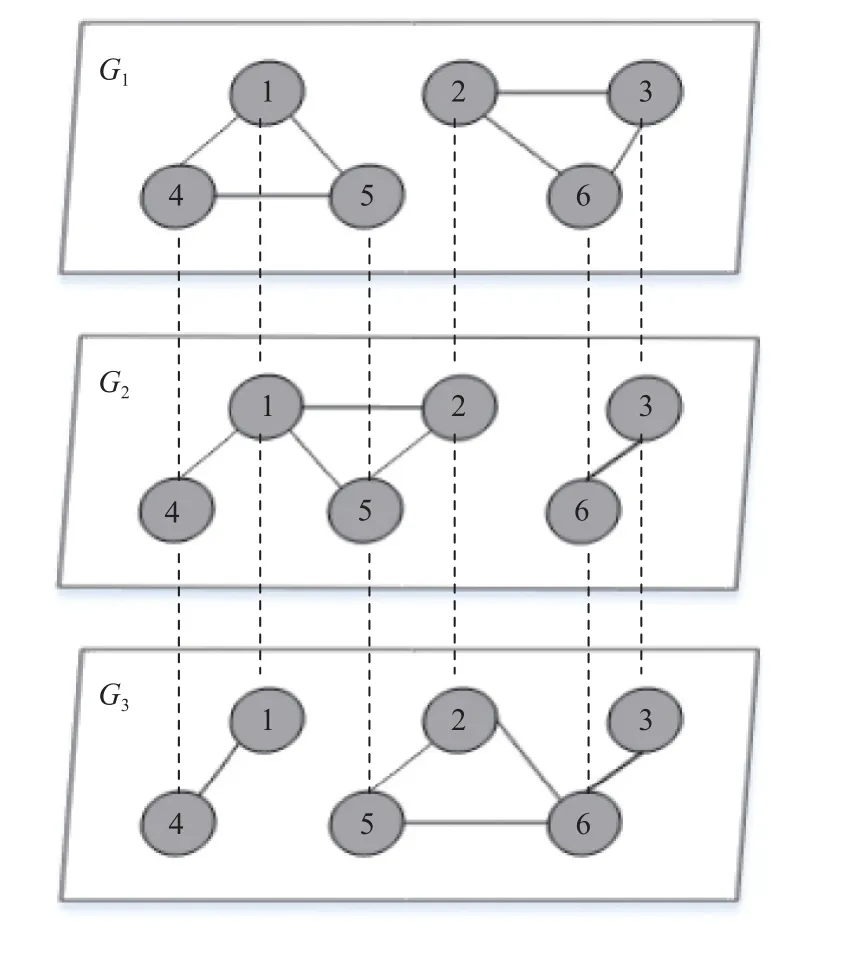
Fig.1 An example of multi-layer network图1 多层网络示例
给定一个L层的多层网络 GL=(G,A),针对每层网络Gα=(V,Eα)分别多次利用传统单层网络社区发现算法得到该层的社区结构为其中表示第 α 层 网络共生成Mα个基社区划分,则多层网络 GL的基社区结构表示为B={B1,…,Bα,…,BL},基于集成的社区发现算法的目的是基于各层网络产生的基社区结构B={B1,…,Bα,…,BL},通过集成函数获得给定多层网络 GL=(G,A)的最终社区划分结果C*={C1,C2,…,Ck} ,且 ∪ki=1Ci=V,Ci∩Cj=∅, 其 中k表示最终社区个数.多层网络总的社区结构划分方案个数为
2.2 基于2 阶段集成的多层网络社区发现算法
本文算法的主要步骤如图2 所示,主要包括基社区划分生成、局部集成、全局加权集成3 个步骤.具体地:1)基社区划分生成是指在多层网络的每一层分别多次利用相同的传统单层网络社区发现算法产生一组基社区划分;2)分别基于单层网络生成的基社区划分和其他各层网络得到的基社区划分中最优的社区划分信息对各层进行局部集成得到局部社区划分结果;3)分别对局部集成得到的社区划分及各个社区的重要性进行度量并进行全局加权集成得到最终社区结果.
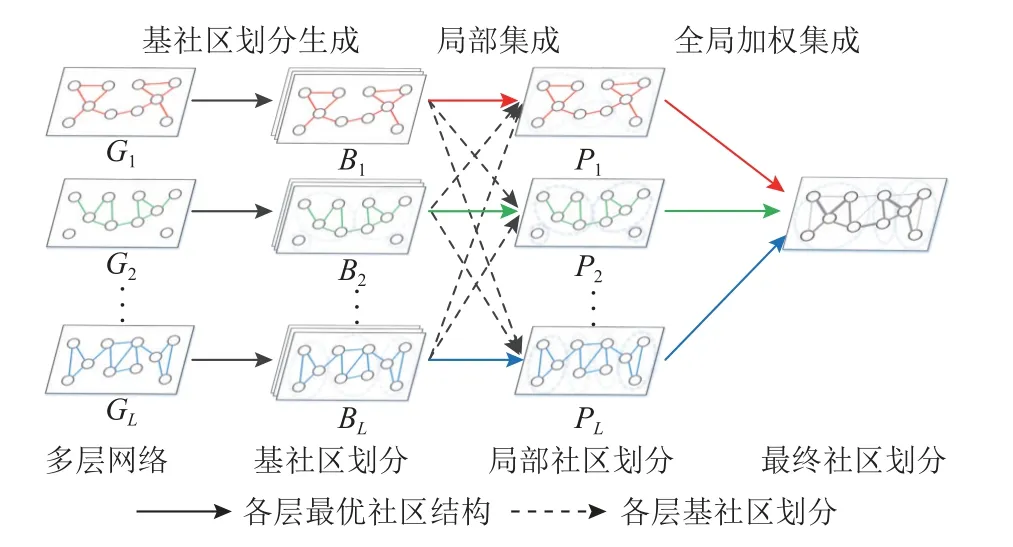
Fig.2 Illustration of our proposed algorithm process图2 本文算法流程示意图
2.2.1 基社区划分生成
该步骤的目的是为不同层的网络分别生成多组准确性高、差异性强的基社区划分.给定一个L层的多层网络 GL=(G,A) ,在每层网络Gα=(V,Eα)分别多次利用传统单层网络社区发现算法获得该层的社区划分表示第 α层网络共生成Mα个基社区划分.为了生成准确性高、多样性强的基社区划分,本文采用经典的LM 算法[10]对每层网络分别进行社区发现.
2.2.2 局部集成
由于不同层产生的基社区划分之间既存在异质性,又存在一定的相关性.因此,在局部社区划分集成阶段各层结合其他各层的最优社区结构信息进行集成.本文中将各个层中最优的社区划分结果加入其他层,以此达到提升局部模型性能的目的.模块度是社区划分质量优劣的评价指标[26].模块度反映了网络社区结构内部连接的强弱,指的是社区内的边占所有边的比例减去在同样的社区结构下随机放置社区内部的边占所有边的比例的期望值,定义为
其中m表示网络的总边数,A表 示网络的邻接矩阵,ki和kj分 别代表节点vi和vj的 度,当节点vi和vj属于同一个社区时, δ (i,j)=1, 否则, δ(i,j)=0.模块度越高,则社区划分质量越高.针对第 α层网络获得的基社区划分Bα={B1α,B2α,…,BαMα},可以通过计算各个划分下的模块度指标来选出第 α层中最优的基社区划分.因此,在进行局部集成时,每一层的基社区划分由该层产生的Mα个 基社区和其他L-1层分别选出的最优社区划分组成.基于基社区划分信息,从局部角度每层分别构造节点之间的共协矩阵Aα(1 ≤α ≤L),记为
其中nij表示在第 α层中节点vi和vj在参与集成的基社区划分中被分配到同一个社区的数量,Mα+L-1是参与集成的社区划分的数量.基于共协矩阵,利用层次聚类即可得到每层的局部社区划分结果Pα(1 ≤α ≤L), 则多层网络 GL的局部社区划分结果记为E={P1,P2,…,PL}.
2.2.3 全局加权集成
在集成过程中,不同社区划分以及社区的优劣均会对最终社区的检测产生不同的影响.本节通过社区划分和社区质量进行评价来对集成过程进行加权.局部社区划分结果E中,每层网络的Pα的优劣通过该划分方案运用到其他层网络上的模块度来衡量,定义为
其中mβ表 示第 β 层 网络的总边数,Aβ表示第 β层网络的邻接矩阵,kβi和kβj分别代表节点vi和vj在 第 β层网络中 的 度,当 节 点vi和vj在Pα属 于 同 一 个 社 区 时,δα(i,j)=1, 否则, δα(i,j)=0.如果Q(Pα,Gβ)越高,则表示相对于第 β层Pα的质量越优.因此,在全局集成中第 α 层 获得的Pα的权重定义为
然 后,对 E={P1,P2,…,PL} 中 各 层Pα(1 ≤α ≤L)的 权重进行归一化,则有
信息熵是信息论中用于度量系统不确定性的一种重要度量方法.如果一个社区结构相对其他划分越稳定,则表明该社区的不确定性越小、可靠性越强,该社区在集成过程中的权重越大.
局部社区划分结果 E={P1,P2,…,PL} 中第 α层的社 区 划 分 记 为Pα={C1α,C2α,…,Cnαα}, 其 中Ciα表 示Pα中的第i个社区,nα表示Pα中 社区的数量.因此, E中所有社区可以表示为
其中Ci表 示第i个社区,nC表 示 E中所有社区的总个数.
给定一个社区Ci∈C 和网络层Gα的Pα∈E,如果社区Ci不 属于Pα, 那么Ci中 的节点可能属于Pα中的多个社区,Ci相 对于Pα的 不确定性可以通过考虑Ci中的对象在Pα中各个社区中的分布来进行计算.那么,社区Ci关 于第 α 层网络Gα的Pα的不确定性可表示为
其中
其中nα表示社区划分Pα中的社区数量,Cαj表示Pα中的第j个社区,表示2 个社区中共有节点的个数, |Ci|表 示Ci中 节 点的 个 数.p(Ci,Cαj)∈[0,1],所以Hα(Ci)∈[0,+∞).
因此,Ci关 于多层网络 GL的局部社区划分 E的不确定性可以通过Ci关 于 E中每层网络的社区划分结构的不确定性的和来表示,即
基于信息熵来衡量每个社区关于局部社区划分E的不确定性,那么进一步可通过归一化来衡量E中每个社区的权重,即
由于HE(Ci)∈[0,+∞) , 所以W(Ci)∈[0,1],即一个社区的不确定越小,则该社区的可靠性就越高,在集成过程中的权重越大.
基于式(8)(13)给出的社区划分以及社区的权重,从全局角度构造节点之间的加权共协矩阵,表示为
其中
其中Clsα(vi)表 示节点vi在Pα中所属社区的标签.
基于加权共协矩阵,通过层次聚类获得多层网络 GL的最终社区划分结果C*={C1,C2,…,Ck}.
基于以上对各阶段集成过程的描述,本文提出的基于2 阶段集成的多层网络社区发现算法描述如算法1.
算法1.基于2 阶段集成的多层网络社区发现算法.
输入:多层网络 GL=(G,A) ,社区划分个数k,各层网络社区基划分次数M;
输出:多层网络 GL的最终社区划分结果C*={C1,C2,…,Ck}.
① 在每层网络上利用传统的LM 社区发现算法获得基社区划分结果,记为B={B1,B2,…,BL};
② forBα∈B
④ {B1,…,Bα-1,Bα+1,…,BL}←; /*将添加到B中除Bα外的其他集合中*/
⑤ end for
⑥ forGα∈G
⑦Aα←Bα; /*根据式(5)计算共协矩阵*/
⑧Pα←Aα;/*利用层次聚类获得局部社区划分*/
⑨ end for
⑩ forPα∈E
⑪W(Pα)←Pα;/*根据式(7)计算局部社区划分的权重*/
⑫ end for
⑬(Pα)←W(Pα);/*根据式(8)对权重进行归一化 */
⑭ forCi∈E
⑮HE(Ci) ←Ci;/*根据式(12)计算社区不确定性*/
⑯ end for
⑰W(Ci)←HE(Ci);/*根据式(13)计算各个社区权重*/
⑱ 根据式(14)构造加权共协矩阵,并利用层次聚类得到最终社区结构C*={C1,C2,…,Ck}.
2.3 时间复杂度分析
本文提出的基于2 阶段集成的多层网络社区发现算法主要包括3 个步骤:1)基社区划分生成;2)局部集成;3)全局加权集成.
在步骤1 中采用LM 算法[10],假设一个单层网络的边的数量为e,则其时间复杂度为O(e),所以步骤1的时间复杂度为O(LMe).步骤2 中主要包括构造共协矩阵,因为Bα中 的社区划分数量为Mα+L-1,因此其时间复杂度为O((Mα+L-1)N2);此外,利用层次聚类算法获得局部社区划分结果的时间复杂度为O(N2),所以步骤2 的时间复杂度为O(L(Mα+L-1)N2+LN2).步骤3 通过信息熵来计算各个社区的稳定性,假设步骤2 得到的总社区数量为nC,则计算社区不稳定性的时间复杂度为O(nC),基于共协矩阵利用层次聚类计算最终社区划分结果的时间复杂度为O(N2),所以步骤3 的时间复杂度为O(nC+N2).因此,算法的总时间复杂度为O(LMe+L(Mα+L-1)N2+LN2+nC+N2).由于L,M,nC均 小于节点个数N,所以算法的总时间复杂度为O(N2).
3 实验分析
为了验证本文算法的有效性,与已有的多层网络社区发现算法在人工合成多层网络和12 个真实多层网络数据集上进行了实验比较分析.
3.1 数据集
3.1.1 人工合成多层网络
为了生成人工合成多层网络数据,本文采用了Bazzi 等人[27]提出的算法.算法参数设置为:网络的层数L= 3,5,7,每层网络的规模N= 1 000 或N=5 000,社区个数分别为10 和50,其中每个节点都出现在每一层中,即在这些网络中分别总共有3 000,5 000,7 000,15 000,25 000,35 000 个节点,节点的度设置为其算法默认值,即最小度为3,最大度为150.混合参数 µ∈[0,1], µ的值越接近1,生成网络的随机性越强.参数∈[0,1]表 示层间相关系数,当=0时,表示产生的多层网络各层之间社区划分是相互独立;当=1时,所产生的多层网络各层之间的社区划分是相同的.由于本文算法为通过集成策略产生统一的社区划分,因此选择参数=1.
3.1.2 真实多层网络
实验中采用的真实多层网络数据集的基本情况如表1 所示.所有真实网络数据的社区划分未知.
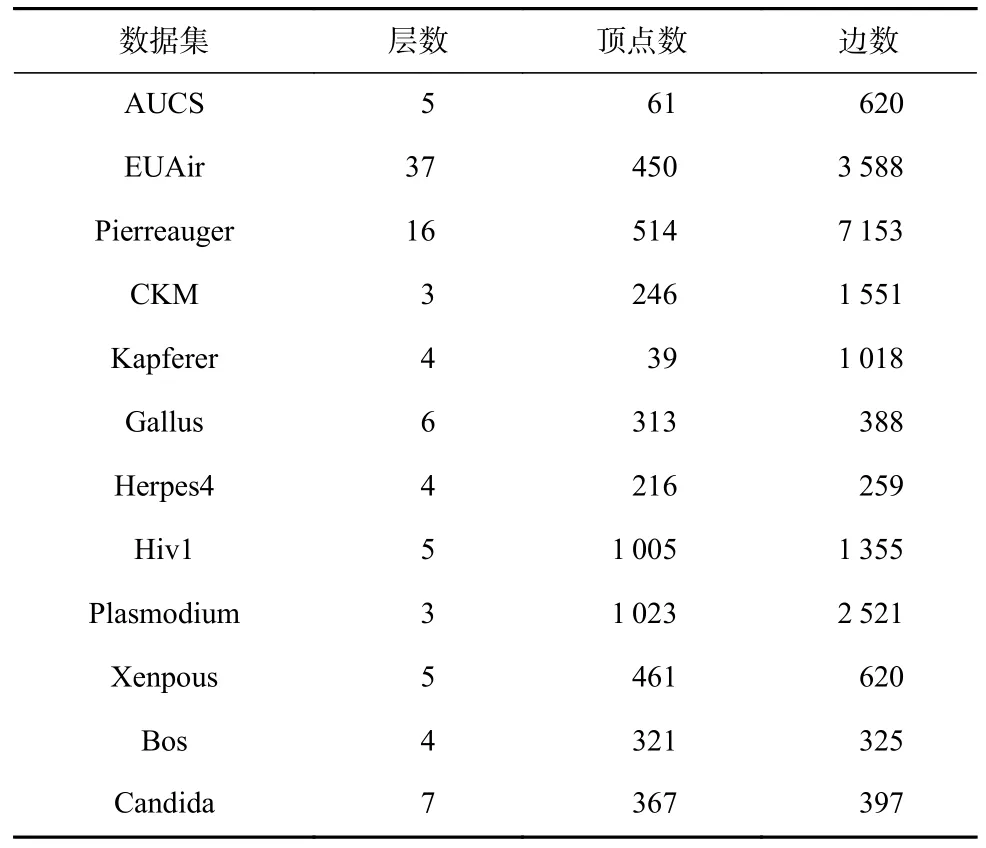
Table 1 Real Multilayer Networks表1 真实多层网络
AUCS 数据集描述某大学研究部门的61 名员工节点(包括教授、博士后、博士生和行政人员)之间的Facebook 关系、午餐关系、合作关系、休闲关系和工作关系[28].EUAir 数据集是欧洲航空交通网络,每层网络对应在欧洲运营的不同航空公司[29].Pierreauger数据集表示天文台科学家之间的协作关系,每一层代表一种协作任务[30].CKM 数据集由美国4 个城镇的246 名医生组成,主要讨论网络关系对医生用药决策的影响,包括通常找谁获取用药建议、经常与谁讨论和与谁关系最好3 层网络[30].Kapferer 网络中节点为裁缝店的工人,关系为他们之间的工作和友谊互动[31].
另外,在包含相互作用数据集的生物通用存储库中选取了Gallus[32],Herpes4[33], Hiv1[33], Plasmodium[32],Xenopus[33], Bos[32],Candida[32]共7 个多层网络数据集.这些网络代表蛋白质之间的相互作用,不同的层对应于不同性质的相互作用,即直接作用、物理关联、共定位、关联、抑制、增强和合成遗传相互作用.每种生物体所对应的层数为3~7 不等.
3.2 评价指标
当数据集的真实社区结果未知时,采用Mucha等人[18]提出的多层网络模块度QM来评价多层网络的社区质量,定义为
其中 µ表示多层网络中的连接的数量,分辨率 γ以控制每层网络的社区规模和数量.Ai jα表 示网络第 α层的邻接矩阵节点vi和 节点vj之 间的连接关系, δαβ在第α 层和第 β 层 为同一层时为1,否则为0; δij在 节点vi和节点vj为 同层节 点时为1,否则为0.Cjαβ表 示 α 层 和β层之间与节点vj的 层间连边数,表示节点vi在 α 层上的度,表示 α层的总边数.如果节点vi和 节 点vj的 社 区 分 布 相 同,则 δ(giα,gjβ)=1,否 则为0.
对于有真实社区划分的数据集,利用标准化互信息(NMI)[34]来评价社区划分结果的质量,NMI定义为
其中X和Y分别表示数据集的真实社区划分结果和算法得到的社区划分结果,cX和cY分别表示X和Y中的社区数量,是一个混淆矩阵,其元素Nij表示在X的社区i与Y的社区j中共同出现的节点数量,Ni表示的第i行的元素的和,Nj表示的第j列的元素的和,N表示节点数量.NMI(X,Y)的范围为[0,1],如果X和Y完全相同,则NMI(X,Y) =1;如果X和Y完全不同,则NMI(X,Y)=0.
3.3 对比方法及参数设置
本文算法与已有多层网络社区发现基线方法进行了比较,代表性方法包括PMM[24],SCML[35],PM[36],CoReg[37],AWP[38],EVM[39].
根据已有文献实验分析中的建议,对基线方法的参数进行了设置.其中,本文方法与基线方法PMM,SCML,PM,CoReg,AWP 共同的参数为社区个数k,为了比较的公平性,对于社区已知的人造网络个数k均设置为真实的社区个数,对于社区未知的真实网络将社区个数k设置为其中N表示节点个数,各个算法分别在不同的k值下运行,并从结果中选取最优值进行比较.PMM 算法中结构特征的数量可以是1~(N-2)(N为节点总数)之间的任意数字,根据建议,对于人工多层网络和真实多层网络均设置了2 个值,人工多层网络比较低的常数为50,真实多层网络比较低的常数为10,用PMMl来表示;另一个是根据节点总数来设定的值,2 类数据集上都设置为N/2,用PMMh来表示,k-means 算法执行的次数设置为10.SCML 算法中正则化参数 λ= 0.5;PM 算法中参 数p=-10 ; CoReg 算 法 正 则 化 参 数 λ=0.01;EVM算法正则化参数 γ=0.5.本文算法中各层网络生成的基社区划分个数M= 10.
3.4 实验结果分析
3.4.1 人工网络实验结果分析
在不同的参数下生成了60 个不同的人工合成网络,针对各个网络,对比算法均在不同参数设置下运行10 次,然后取结果的平均值进行比较.各个算法在不同人工网络的NMI值随网络参数 µ的变化如图3所示.随着 µ的逐渐增大,不同算法的性能均出现了下降趋势.这是因为随着 µ的增大网络的随机性变强,网络蕴含的社区结构复杂导致社区发现算法识别正确社区的难度加大.当多层网络的节点数量N= 1 000时,PMMh产生了较差的结果,且在所有网络中,PMMl和PMMh产生的结果有着较大的差异,说明不同的结构特征数量对PMM 产生了较大的影响,而其取值为1~(N-2),特别对于规模较大的网络,选取合适的结构特征数量并不容易.其他算法的结果都随着 µ的变化出现了较大的波动,从图3 可以看出本文算法在大部分情况下优于其他算法.当多层网络的节点数量N= 5 000 时,基本上所有算法的结果随着µ的增大而减小.例如,PM 算法的结果在L= 3,5,7 的情况下分别在 µ= 0.4,0.5,0.6 的时候明显下降,PMM算法对于不同的提取的结构特征数量值,结果产生了较大的差异;AWP 算法的结果在3 种不同层数的网络中 µ<0.7 时均表现较好,但在 µ = 0.7 出现了明显下降; SCML 算法表现较好,这是因为SCML 算法通过将包含在单个图层中的信息转换为Grassmann 流形上的子空间并利用Grassmann 流形上的距离分析找到一个具有代表性的子空间,最后在这个代表子空间上进行聚类.但是,SCML 的聚类结果容易受到与代表性子空间距离更近的单个图层子空间上聚类结果的影响,当所有单个图层都包含丰富的信息时,SCML 将产生更好的结果,若与代表性子空间距离更近的单个图层上的聚类质量较差时也会导致SCML产生较差的结果.下面我们选取L= 3,N= 5 000, µ=0.5 和L= 3,N= 1 000, µ= 0.6 这2 种不同情况的人工网络来说明SCML 算法为何在N= 5 000 时取得较好的结果.如表2 所示,在L= 3,N= 5 000, µ= 0.5 上代表性子空间与第2 层的子空间距离最近,且从表2 中SCML 算法在单层网络上得到的结果和NMI值,可以看出各层网络均包含较为丰富的信息,所以SCML得到了更好的结果.如表3 所示,在L= 3,N= 1 000,µ= 0.6 上代表性子空间与第2 层的子空间距离最近,与表2 不同的是该网络的第2 层得到了低质量的聚类结果,SCML 产生了较差的结果.说明当多层网络的各层网络中都包含较为丰富的信息时,SCML 产生更好的结果,而当各层网络中存在信息较少且该层网络的子空间与SCML 计算所得的代表性子空间距离即使较近时,SCML 也会忽略信息较多的层,从而导致最终产生较差的结果.基于以上2 个人工网络对本文提出的方法进行分析,在L= 3,N= 5 000, µ= 0.5上,本文算法的NMI分别为0.802 1,0.813 1,0.802 3.可以看出,该网络中各层都包含了较为丰富的信息,通过式(14)进行全局加权集成后,得到的NMI= 0.850 1;在L= 3,N= 1 000, µ = 0.6 上,本文算法的NMI分别为0.544 0,0.224 7,0.024 7.可以看出该网络中各层之间的差异性较大.
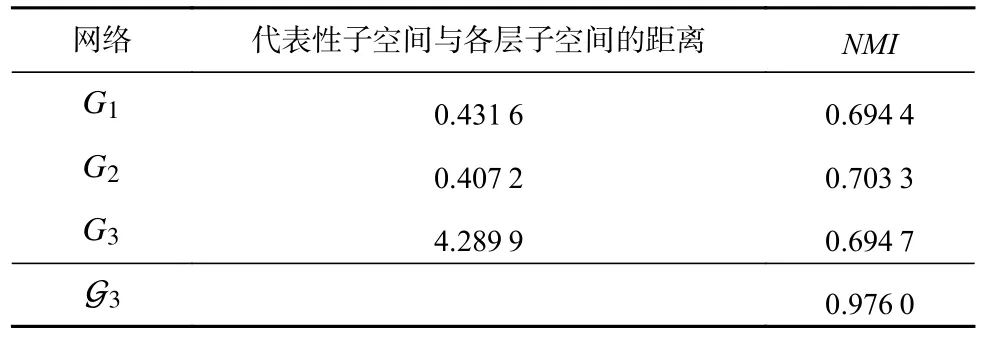
Table 2 Result Analysis of SCML on Network with L=3, N=5 000, μ=0.5表2 SCML 在L=3, N =5 000, μ=0.5 网络上的结果分析
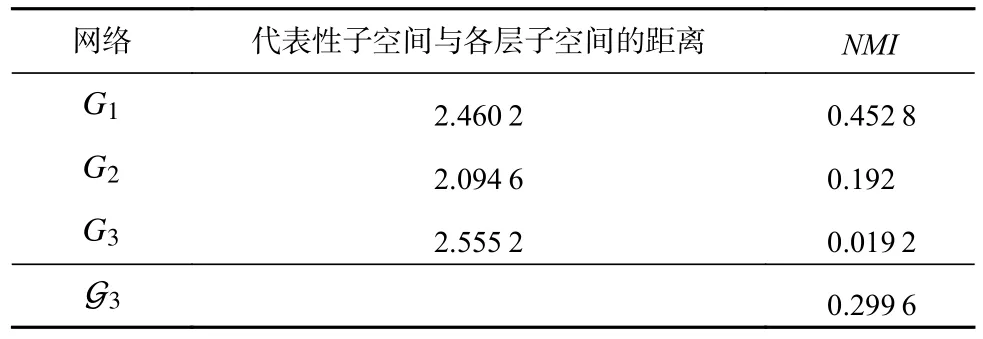
Table 3 Result Analysis of SCML on Network with L=3, N=1 000, μ=0.6表3 SCML 在L=3, N=1 000, μ=0.6 网络上的结果分析
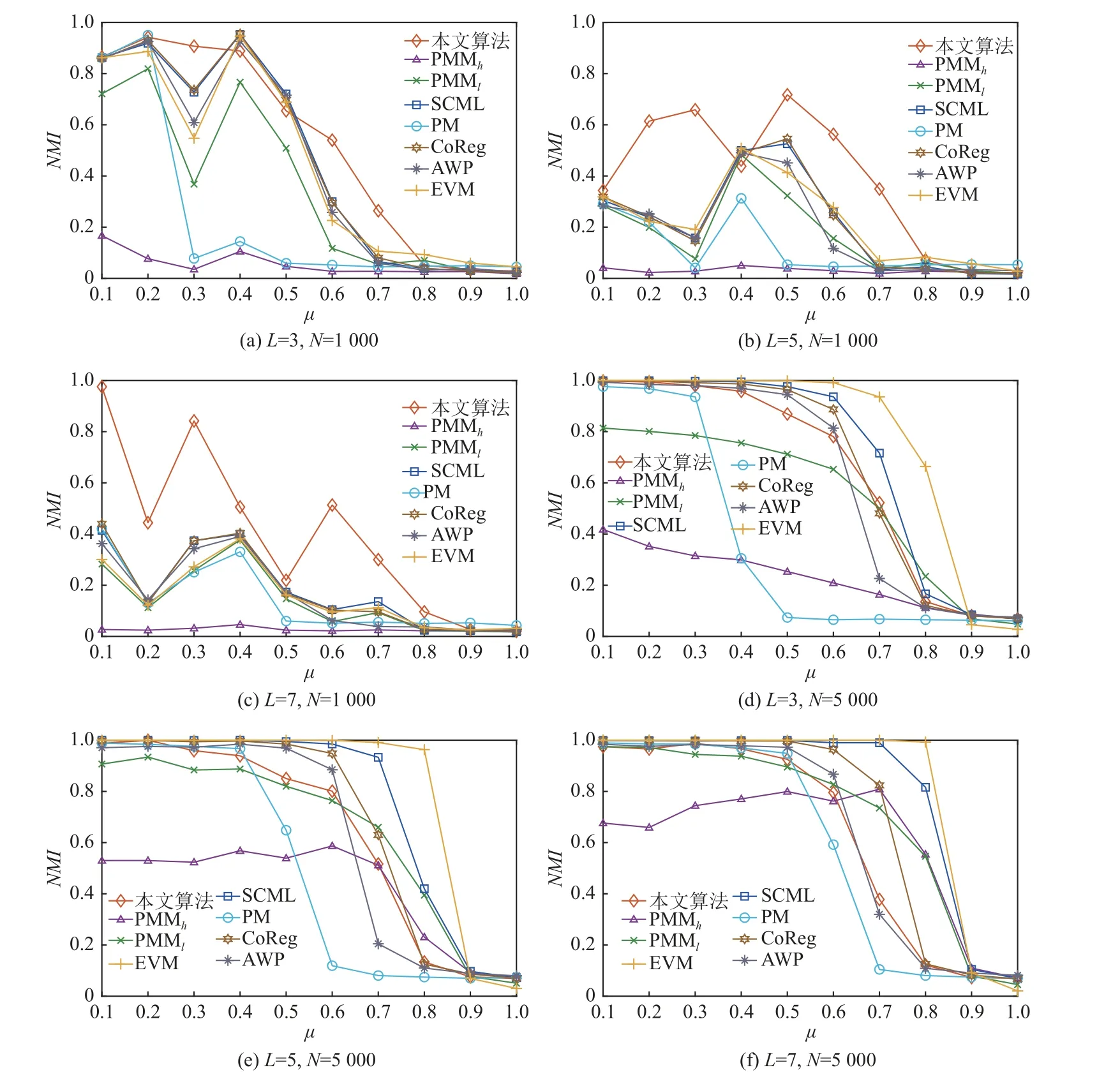
Fig.3 Comparison results of NMI on synthetic networks图3 不同算法在合成网络上的NMI 比较结果
通过式(14)进行全局加权集成后,得到的最终结果的NMI=0.548 9.通过对比表2、表3 与本文算法得到的NMI值可以看出L= 3,N=5 000, µ=0.5 中各层网络包含信息较为平均,而L= 3,N=1 000, µ=0.6 中各层网络包含信息的差异较大,所以当N=5 000 时,由于单层网络之间差异较小,且随着 µ的增大,各层网络社区结构难以识别,导致各层网络上得到的基社区划分较差,从而导致经过集成产生的社区质量也较低;当 µ<0.7时,本文算法在3 种不同层数的网络上的实验结果变化较小,说明本文算法的鲁棒性较强.CoReg 和EVM 同样在N=5 000,即单层网络差异较小的人工网络上表现出了良好的性能,而在单层网络差异较大的人工网络上表现较差.
3.4.2 真实网络实验结果分析
不同算法在真实网络的实验结果如表4 所示,其中每个算法在不同参数设置下均运行10 次,从不同社区个数得到的结果中选取最优模块度值进行比较.对不同算法在每个数据集上社区发现结果的最优结果和次优结果进行加粗标注.从表4 可以看出,本文算法在除AUCS 之外的11 个数据集上都取得了最优结果或次优的结果,其中在EUAir ,Gallus,Herpes4,Hiv1,Plasmodium,Xenopus,Bos 共7 个数据集上本文算法的结果明显优于次优的结果.总之,本文算法在真实数据集上表现出了较为良好的性能.

Table 4 Comparison of Experimental Results on Real Networks in Terms of QM表4 真实网络实验结果的QM 比较
3.4.3 鲁棒性分析
为了验证本文算法的有效性受基社区划分数M变化的影响,对采用 µ=0.3 时不同规模的6 个人工多层网络和部分层数较少的真实多层网络进行了鲁棒性 测 试.其 中,M∈{10,20,30,40,50},对 于 不 同 的M值,取本文算法在每个网络上执行10 次的结果的平均值进行比较,实验结果如图4 和图5 所示.
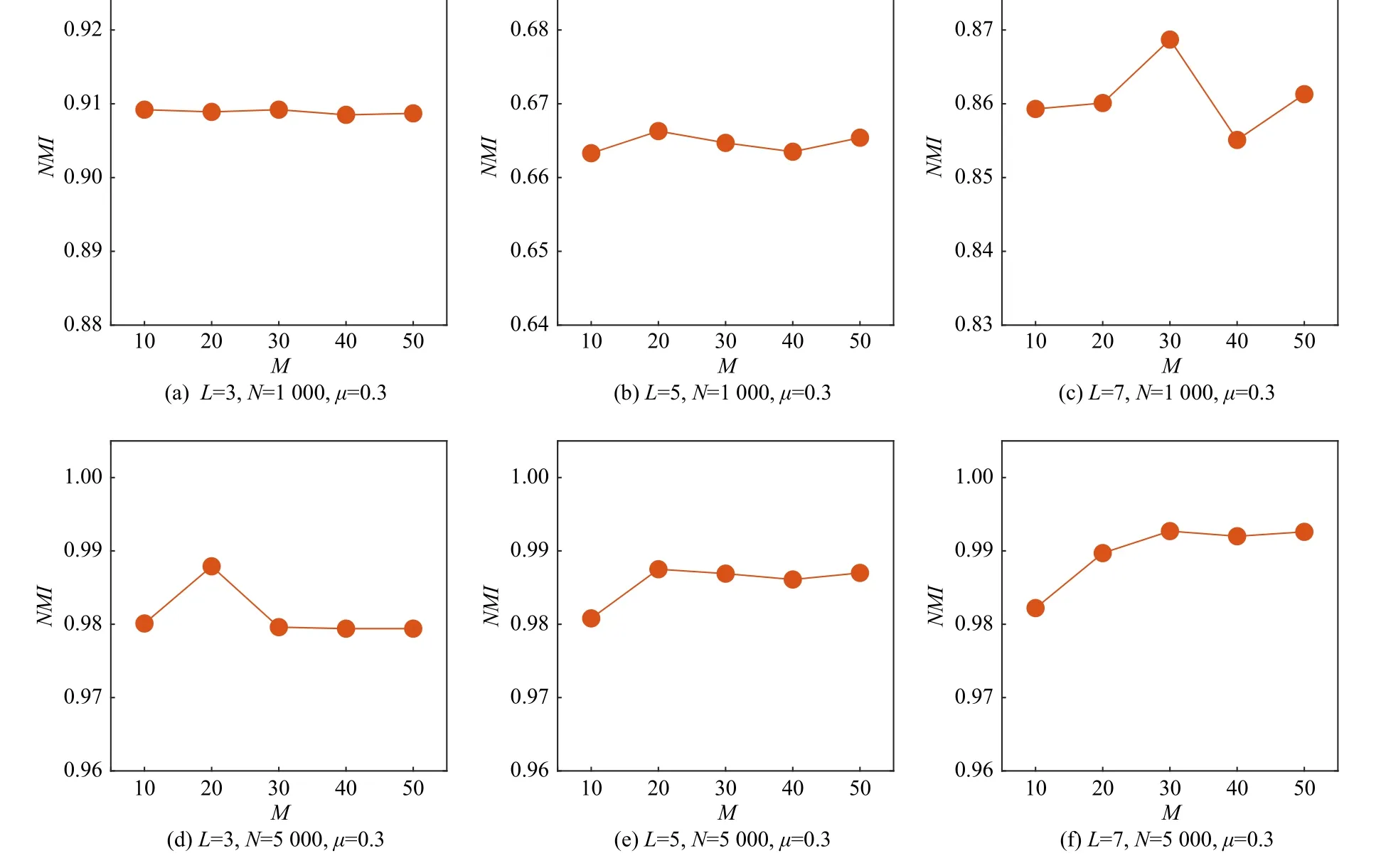
Fig.4 NMI of the proposed algorithm changes with varying ensemble number M图4 本文算法的NMI 随基社区划分数M 的变化
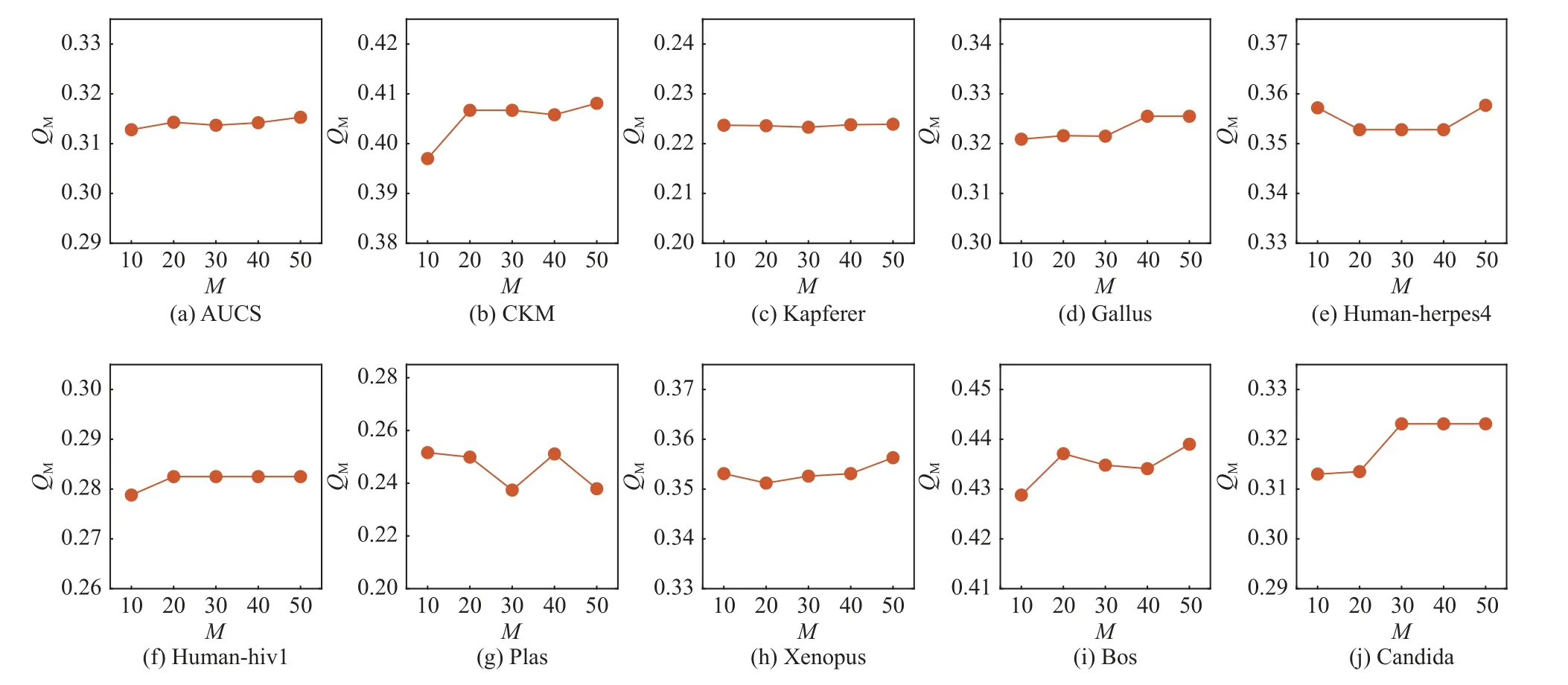
Fig.5 Q M of the proposed algorithm changes with varying ensemble number M图5 本文算法的QM 随基社区划分数M 的变化
在人工多层网络数据集中,采用NMI指标对社区划分结果进行评价,统计在不同M下NMI的变化情况.由图4 可知,当L= 7,N=1 000, µ=0.3 时本文算法的NMI值出现了最大的波动(0.013),其次当L=7,N=5 000, µ=0.3 时NMI值为0.01,在其他人工网络数据集上NMI值的波动范围均在0.01 以内.在真实多层网络数据集中,通过多层模块度指标QM对各个结果的变化范围进行分析.在Plas 数据集上,本文算法的结果在不同的M值下QM值的波动为0.015,在CKM 和Candida 数据上的QM值的波动范围均为0.011,而在其他数据集上不同的M值下QM值变化范围均小于0.01.结果表明,本文算法的性能受基各层社区划分个数M的影响较小,具有良好的鲁棒性.
4 总 结
近年来,有效融合多层网络信息并对其进行社区发现成为了一个重要的研究内容.为此,本文提出了一种基于2 阶段集成的多层网络社区发现算法.首先,第1 阶段在各层进行局部集成时结合了其他层的最优社区划分信息,有效利用了不同网络层社区结构的相关性;其次,第2 阶段中基于其他网络层的社区结构信息对各层融合得到的社区划分及社区结构的重要性进行评价加权,再进行全局加权集成,综合考虑了各层局部社区划分结果对集成的影响;最后,通过在人工生成多层网络和真实多层网络上进行实验分析,对本文算法的有效性和鲁棒性进行了验证.然而,本文提出的算法面临时间复杂度较高的问题,在未来的工作中将考虑如何提高算法的计算效率来应对大规模多层网络社区发现面临的挑战.
作者贡献声明:赵兴旺提出论文算法思想、设计实验方案并修订论文;张珧溥完成实验并撰写论文;梁吉业提出算法的指导意见和审核论文.
