MIBS 分组密码的改进积分攻击
2023-12-15毛永霞吴文玲
毛永霞 吴文玲 张 丽
(中国科学院软件研究所 北京 100190)
(中国科学院大学 北京 100049)(yongxia2018@iscas.ac.cn)
近20 年来,伴随着物联网技术的飞速发展,资源受限设备如低成本的RFID(radio frequency identification)标签、无线传感器、嵌入式系统等的应用越来越广泛.为资源受限设备研制低成本、低能耗的轻量级密码算法是一项具有挑战性的工作,吸引了许多密码学者的关注.例如,Leander 等人[1]设计了DES(data encryption standard)加密算法的一个轻量级变体DESL;Poschmann 等人[2]设计了一个比DESL 更强的DES 的变体DESXL;Bogdanov 等人[3]提出了著名的轻量级密码算法PRESENT;Banik 等人[4]设计了比PRESENT 更安全、高效的轻量级密码算法GIFT.
MIBS 是一个适用于资源受限环境的轻量级分组密码算法,由Izadi 等人[5]在CANS 2009 会议上提出.针对MIBS 分组密码算法的现有分析结果包括差分分析[6]、线性分析[6]、积分分析、不可能差分分析[7]等.目前对于MIBS-64 最好的分析结果是14 轮的差分分析,成功概率为50.15%;对MIBS-80 最好的分析结果是18 轮的线性分析,成功概率为72.14%.
积分分析是由Knudsen 等人[8]在FSE 2002 上提出来的,由于它的思想原型首先被应用于分组密码Square[9],因此也被称为Square 攻击.积分分析是当前评估分组密码算法安全性的基础分析方法之一,已经在许多分组密码算法上得到了较好的攻击结果,例如AES[10], PRESENT[11]等.可分性是积分分析的推广,在EUROCRYPT 2015 上被Todo[12]提出.Todo 结合密码算法非线性部件的代数次数,优化了积分性质,使得积分特征能够用一种更精确的方式推导.一个显著的应用是第一次在理论上对全轮的MISTY1进行了积分攻击[13].在ASIACRYPT 2016 上,Xiang 等人[14]将基于混合整数线性规划(mixed integer linear programming, MILP)建模的方法引入基于比特的可分性,进一步提高了积分区分器可自动化搜索的密码算法的规模.2017 年,Todo 等人[15]对上述MILP 模型进行了补充,并将其应用于多个流密码算法的立方攻击,得到了多个流密码当时最好的密钥恢复攻击.近几年,对分组密码算法的积分区分器搜索的改进主要围绕改进非线性层[16-19]和线性层[19-24]的模型进行.
目前,对MIBS 算法的积分分析已经存在一些结论.2013 年,于晓丽等人[25]基于一个5 轮的积分区分器,利用高阶积分技术将该区分器向前扩展3 轮,分别对MIBS-64 和MIBS-80 进行了8, 9, 10 轮的积分攻击.2014 年,潘志舒等人[26]构造了MIBS 的5 轮积分区分器,利用Feistel 结构的等价结构以及MIBS 密钥编排算法中主密钥和轮密钥的关系,给出10 轮MIBS 算法的积分攻击.2016 年,伊文坛等人[27]利用零相关线性逼近和积分区分器之间的联系,推导出MIBS 的8 轮积分区分器,进而对11 轮的MIBS-80 进行了攻击.2021 年,李艳俊等人[28]基于5 轮的积分区分器,向前、向后各扩展3 轮,给出了一个11 轮MIBS-64 的积分攻击.
部分和(partial sum technique)技术是Ferguson 等人[10]在分析Rijndael 时提出的一种降低攻击复杂度的方法,是改进积分攻击的有效方法.该方法主要利用积分攻击需要对中间状态进行求和的特点,通过压缩密钥恢复过程中的数据量来有效减少计算时间,例如,将对6 轮Rijndael 的密钥恢复时间复杂度从272降低为 249[10].
本文研究MIBS-64 和MIBS-80 的积分分析,主要贡献有4 个方面:
1) 针对密钥编排算法,利用密钥搭桥技术,得到了轮密钥之间的一些相关性质;
2) 构造了MIBS 的8 轮和9 轮积分区分器;
3) 对于MIBS-64,基于8 轮的积分区分器,在区分器末尾增加4 轮,给出了12 轮的密钥恢复攻击;
4) 对于MIBS-80,基于9 轮积分区分器,在末尾增加5 轮,给出了14 轮的密钥恢复攻击.
3)和4)这2 个攻击是目前对MIBS-64 和MIBS-80 已知的最好的积分攻击,与已有积分攻击结果的对比如表1 所示.
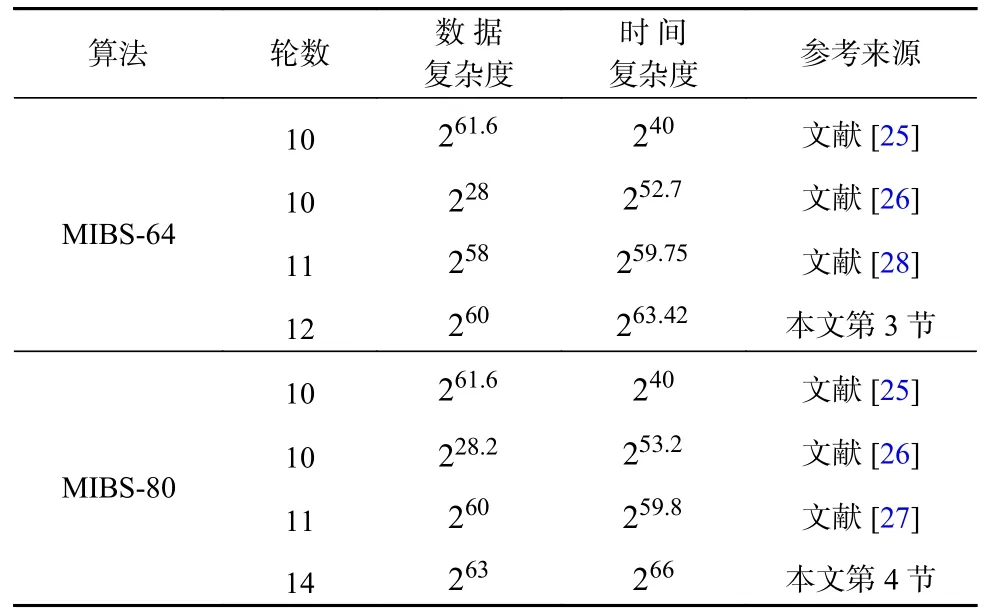
Table 1 The Integral Attack Results on MIBS表1 对MIBS 的积分攻击结果
1 预备知识
1.1 符号说明
C[i:j]: 密文的第j比 特 到 第i比特;
Xt,[i:j]: 第t轮中间状态的第j比特到第i比特;
Xti: 第t轮中间状态的第i个半字节;
skt,[i:j]: 第t轮密钥的第j比特到第i比特;
skit: 第t轮密钥的第i个半字节;
state[i:j]: 中间状态的第j比特至第i比特;
S/St: S 盒函数/第t个S 盒函数;
a/c: 一个活跃比特/常数比特;
A / C: 一个活跃半字节/常数半字节;
B / U: 一个平衡半字节/未知半字节;
>>>: 右循环移位操作;
||: 字符串的连接操作;
◦ 函数的复合符号.
1.2 MIBS 加密算法简介
分组密码MIBS 整体采用Feistel 结构,轮函数使用SP 结构,其分组长度64 b,MIBS 支持64 b 和80 b这2 种密钥长度,分别记为MIBS-64 和MIBS-80,迭代轮数为32 轮.MIBS 中所有的运算都是基于半字节的.
设MIBS 的轮函数为F,第i轮的轮密钥为Ki,输入 为 (Xi,Xi-1), 那 么 输 出 为 (Xi+1,Xi), 其 中Xi+1=F(Xi,Ki)⊕Xi-1.轮函数F由异或子密钥层AK、S 盒层(4×4的S 盒)和线性变换P组成,记为F=P◦S◦AK,具体如图1 所示.

Fig.1 Round function of MIBS图1 MIBS 的轮函数
设线性变换P:(F42)8→(F42)8的 输入为y=(y7,y6,y5,y4,y3,y2,y1,y0), 输出为y′=(y′7,y′6,y′5,y′4,y′3,y′2,y′1,y′0),那么
1.3 MIBS 密钥编排算法简介
MIBS 的密钥编排采用了与PRESENT 的密钥编排相同的设计原则.
1)MIBS-64 的密钥编排算法
设MK64是 长度为64 b 的主密钥,记为MK64=(k63,k62,…,k0).设密钥编排算法第i轮的中间状态为statei.由主密钥生成长度为32 b 的轮密钥Ki( 1 ≤i≤32)的过程为:
其中RC表示轮计数,第i轮 状态statei的左32 b 作为第i轮的轮密钥.
2)MIBS-80 的密钥编排算法
设MK80是 长度为80 b 的主密钥,记为MK80=(k80,k79,…,k0).设密钥编排算法第i轮的中间状态为statei.由主密钥生成长度为32 b 的轮密钥Ki( 1 ≤i≤32)的过程为:
其中第i轮状态statei的左32 b作为第i轮的轮密钥.
1.4 密钥搭桥技术
密钥搭桥技术最早是在文献[29]中针对AES-192 提出的.该技术的主要作用是根据密钥编排算法,推导出某些轮密钥之间存在的依赖关系,即:从某些轮密钥字节中计算出其他的轮密钥字节,即使这些字节距离很多的扩散步骤.在FSE 2016 上,Lin 等人[30]提出了一个高效的比特迭代型密钥搭桥自动搜索算法,这个算法可以改进几乎所有对分组密码攻击的复杂度.
比特迭代型密钥搭桥自动搜索算法的输入为一个表示密钥编排算法的方程系统和一个想要找到其中变量关系的密钥变量集合 K0,输出是密钥变量集合 K0中存在的密钥桥,具体过程可以划分为2 个阶段:
1)知识传播阶段,主要利用Gauss-Jordan 消元法处理方程系统的系数矩阵;
2)关系导出阶段,根据1)处理之后矩阵的秩,导出密钥间的线性关系,即密钥桥.
2 MIBS 的密钥编排性质和积分区分器
2.1 MIBS 密钥编排的相关性质
针对MIBS-64 和MIBS-80 的密钥编排算法,利用文献[30]的密钥搭桥技术搜索轮密钥之间可能存在的相关关系,即密钥桥.算法1 描述了这一过程.设K表示MIBS 密钥编排算法的所有中间密钥变量的集合, K0表示MIBS-64 第9~12 轮的部分轮密钥集合和MIBS-80 第10~14 轮的部分轮 密 钥 集 合, K1表 示K0可 以扩张到的集合, S表示S 盒的输入输出比特变量集合,Mkey表 示由密钥编排算法生成的密钥方程系统E的系数矩阵.矩阵中变量的顺序为(K-S-K1,S,K1,c), 其 中 K-S-K1表 示 S 和 K1在 K 中的 补 集,c表示常数的列.G(Mkey)表示利用Gauss-Jordan 消元法将Mkey变 为对角矩阵;Gn(Mkey)表示利用Gauss-Jordan消元法将Mkey的 前n列变为对角矩阵.算法1 的目标是找到 K0间潜在的关系式.
算法1.MIBS 轮密钥关系搜索算法.
输入:轮数r、种子密钥K、待测试密钥集 K0;
输出:密钥桥集合R.
①Generate_key_equation(r,K,sk):/*生成种子密钥K与轮密钥sk之间的具体关系式,忽略常数加操作*/
② foriin range ( 0 ,r) do
③E(K,sk)←key_schedule(i,ski);/*ski是第i轮密钥,sk0=K,E是关于K和sk的密钥方程系统*/
④ end for
⑤ returnE(K,sk).
⑥ functionPropagation( K,K0,S,Mkey):/*知识传播阶段,扩展 K0到所有可表出的密钥*/
⑦M←GK-K1-S(M);/*M表示 K-K1-S对应的系数矩阵*/
⑧ forrowinMkeydo
⑨ if 在前 | K-K1-S|行 有1 个row属 于casethen
⑩ 移动x,S(x) ,或者x与S(x)所对应的列;
⑪ ( K1,S)←(K1,S)∪{x}({S(x)},{x,S(x)});/*添加新变量*/
⑫ end if
⑬ end for
⑭ return K1,Mkey.
⑮ functionDerivation( K0, K1,A):/*关系导出阶段,对系数矩阵Mkey中 变量 K1对应的分块矩阵A进行处理*/
⑯A←GK1-K0-S(A);
⑰ forrowinB1do /*B1为 矩阵A中 变量 S对应的分块矩阵*/
⑱ ifRank(B1)≥4-Nthen/*N为 S 中元素在K0中出现的个数*/
⑲ 向A中 增加与φ和x+φ′相应的新行和新列;
⑳ ifRank(B1)>4-Nthen
㉑ 向A中 增加与ψ 和 ψ′相应的新行和新列;
㉒ end if
㉓ end if
㉔ end for
㉕A←GK1-K0-S(A);
㉖ forrowinB2do /*B2是 矩 阵A中 变 量 K0对应的分块矩阵*/
㉗R←导出所有密钥桥;
㉘ end for
㉙ returnR.
行⑨case={case1,case2},其中:
case1=(0,…,0,ex,0,…,0,eS(x),0,…,0,e|K-K1-S|,…,en);
case2={(0,…,0,et,ex,0,…,0,e|K-K1-S|,…,en),(0,…,0,es,eS(x),0,…,0,e′|K-K1-S|,…,e′n),t≠s,et=es=0,ej=c·e′j,j=|K-K1-S|,…,n-1}.
行⑲的 φ 为 S 中剩余的 8-Rank(B1)-N个变量,φ′是关于 φ的线性组合.
行㉑的 ψ 为 S 中剩余的Rank(B1)-4+N个变量,ψ′是关于 ψ的线性组合,它们用于表示可以由S扩展得到的密钥比特.
利用算法1,搜索到了MIBS-64 和MIBS-80 的密钥编排的相关性质——性质1 和性质2.此外,我们也通过密钥编排算法推导验证了性质1 和性质2.
性质1.根据MIBS-64 的密钥编排算法,第11 轮的密钥sk11,[31:17]可 由第12 轮密钥sk12,[16:02]得到;第10轮密钥sk10,[31:30]可 由第12 轮密钥sk12,[01:00]得到;第10轮密钥sk10,[31:15]可 由第11 轮密钥sk11,[16:00]得到;第9 轮的轮密钥sk9,[12:00]可 由第12 轮轮密钥sk12,[31:19]得到,第9 轮的轮密钥sk9,[31:15]可 由第10 轮的轮密钥sk10,[16:00]得到.
性质2.根据MIBS-80 的密钥编排算法,第13 轮的轮密钥sk13,[31:19]可 由第14 轮的轮密钥sk14,[12:00]得到;第12 轮密钥sk12,[31:19]可 由第13 轮的轮密钥sk13,[12:00]得到;第11 轮的密钥sk11,[31:19]可 由第12 轮密钥sk12,[12:00]得 到;第11 轮 的 密 钥sk11,[08:00]可 由 第14 轮 密 钥sk14,[31:23]得 到;第10 轮 密 钥sk10,[31:19]可 由 第11 轮 密 钥sk11,[12:00]得 到;第10 轮 密 钥sk10,[27:00]可 由 第14 轮 密 钥sk14,[31:04]得到.
文献[26]提出了一个关于MIBS-64 的轮密钥和主密钥之间关系的性质.与密钥搭桥技术考虑所有轮密钥之间的具体关系式不同,文献[26]通过密钥编排算法的循环移位操作来判断轮密钥可能涉及的所有主密钥位置.例如,考虑性质1 的密钥桥sk12,[16:02]→-sk11,[31:17].根据文献[26],猜测sk12,[16:02]需 要猜 测 主 密 钥K[39:20], 猜 测sk11,[31:17]需 要 猜 测 主 密 钥K[36:21], 因 此 轮 密 钥sk12,[16:02]与sk11,[31:17]之 间 似 乎 并 不能互相独立推导得出.事实上,根据密钥编排算法写出它们之间的表达式,发现二者是可以互相推导的,而这恰好是密钥搭桥技术的思想.密钥搭桥技术通过处理轮密钥之间的具体关系式,精准地判断出所有潜在的密钥桥.
文献[26]也提出了MIBS-80 的轮密钥和主密钥之间关系的性质.类似地,考虑密钥桥sk14,[12:00]→-sk13,[31:19].那么,根据文献[26],猜测sk14,[12:00]需要猜测主密钥K[79:74,09:00], 猜测sk13,[31:19]需要猜测主密钥K[79:71,06:00].因 此sk14,[12:00]和sk13,[31:19]似 乎 不 能 完 全 互相推导得出.事实上,根据轮密钥之间的关系式,sk14,[12:00]和sk13,[31:19]也 是 可 以 互相推导出的.
2.2 MIBS 的积分区分器
目前,MIBS 最长的积分区分器为5 轮,都是基于加密算法的结构特点推导求得的[25,28].结合文献[14,31]的基于比特自动化建模方法,分别对线性变换和S盒生成约束条件,建立MIBS 的MILP 模型,搜索更长的积分区分器.具体过程为:首先,对MIBS 加密算法的每一个基本操作建模;然后,生成MIBS 的r轮可分性传播的线性不等式系统;接着,给定输入和输出可分性;最后,利用求解器求解r轮可分性传播系统.
MIBS 的加密算法仅包含S 盒、线性变换P、异或操作、置换操作.对于S 盒,利用文献[31]的方法,使用Quine-Mclusky 方法建立约束条件.首先,求出S盒的所有可分迹,然后利用Logic Friday 软件生成约束这些可分迹的合取范式,最后将合取范式转换为线性不等式(具体约束如附录A 所示).
对于置换操作,仅需要改变变量的位置即可.对于异或操作b=a0⊕a1,使用的建模规则为:
另外,还需使用复制操作b→(a0,a1),使用的建模规则为:
线性层中异或操作和复制操作的建模比较简单,只需根据建模规则,直接代入状态变量即可.对于线性变换P,对应的基于半字节的矩阵在附录B 中给出.根据此矩阵和异或操作、复制操作的建模规则,可以直接写出其对应的基于比特的约束不等式(具体参考附录B).
按照式(1)(2)的建模方式迭代r次,MIBS 的r轮可分性传播的线性不等式系统即可生成.然后,挑选仅有几比特为常数.其余比特全活跃的输入状态,确定输入可分性,并且将输出对应的变量写成目标函数,添加到不等式系统中,完成对MILP 模型的建模过程.最后,通过求解不等式系统判断积分区分器的存在性.
根据上面的自动化建模搜索方法,可以构造MIBS 的8 轮积分区分器:从明文集的最高32 比特选择4 比特为常数,其余比特都活跃,那么经过8 轮MIBS 加密之后,输出的最低32 比特都是平衡的.例如,当明文的最高4 比特为常数时,对应的输入和输出可分性表示
当选择的明文集只有1 个比特为常数时,可以构造9轮积分区分器,具体如定理1 所示.
定理1.选择明文集X,满足最高32 比特中的任一比特为常数,其余比特都为活跃比特,即对于一个固定的i∈{0,1,…,31},xi=c;对于任意j≠i,xj=a.那么,该明文集经过9 轮MIBS 加密之后,输出的最低32 比特都是平衡的,即输出值的求和有形式为:
设每一轮的输入可分性 D=D[63:32]||D[31:00], 表2展示了当最高比特为常数时,9 轮积分区分器每一轮中间状态对应的可分性.

Table 2 Division Property of Intermediate States for the 9-Round Integral Distinguisher of MIBS表2 MIBS 9 轮积分区分器中间状态的可分性
3 12 轮MIBS-64 的密钥恢复攻击
本节利用2.2 节中MIBS 的8 轮积分区分器:最高4 位是常数,其余位均活跃,8 轮之后输出的最低32 位是平衡的,在区分器末尾增加4 轮,完成了对12 轮MIBS-64 的密钥恢复攻击,如图2 所示.

Fig.2 Key recovery attack of MIBS-64图2 MIBS-64 的密钥恢复攻击
3.1 攻击过程
整个密钥恢复过程分为6 步,具体攻击步骤为:
Step1.选 择 明 文 集X=X1||X0,X共 260个 明 文,满足明文的第1 个半字节为常数,其余半字节都是活跃的,查询其12 轮MIBS-64 加密之后的密文C=C[63:32]||C[31:00].
Step2.已知密文C,猜测第12 轮的密钥sk12,[31:00],解密计算X11=P◦S(C[63:32]⊕sk12) ⊕C[31:00].
Step3.已知密文和X11,猜测第11 轮的轮密钥sk11,[31:00], 计算X10=P◦S(X11⊕sk11)⊕C[63:32].根据性质1,部分密钥可以根据12 轮的轮密钥直接得到,因此实际只需猜测15 b,即sk11,[14:00].
Step4.已 知X11和X10,猜 测 第10 轮 的 轮 密 钥sk10,[31:00], 计 算X9=P◦S(X10⊕sk10)⊕X11.根 据 性 质1,部分密钥可以根据第12,11 轮的轮密钥直接得到,因此实际只需猜测15b,即sk10,[14:00].
Step5.已知X10和X9, 猜测第9 轮的轮密钥sk9,[31:00],计算X8=P◦S(X9⊕sk9)⊕X10.根据性质1,部分密钥可以根据第12,11,10 轮的轮密钥直接得到,因此实际只需猜测15b,即sk9,[14:00].
Step6.根 据2.2 节,X经8 轮MIBS 加 密 之 后 的低32 比特都是平衡比特.因此,满足Xi,8=0 的密钥可能为正确密钥.筛选概率为 2-32,共得到232+15+15+15×2-32=245个候选密钥.
3.2 利用密钥搭桥与部分和技术降低复杂度
3.1 节的攻击过程已经根据密钥桥调整了需要猜测的密钥个数,下面介绍利用部分和技术降低复杂度.
对于Step2,利用部分和技术,逐个计算X11中每半字节的值.由于S(C[63:32]⊕sk12)=S7(C[63:60]⊕sk12,[31:28])||…||S0(C[35:32]⊕sk12,[03:00]), 根据线性变换P,有式(3)~(10)成立:
2)根据式(4)计算X111.由于在1)中已经猜测了,因此这里只需再猜测和的值.通过猜测的密钥,统计X111的所有可能值出现次数的奇偶性.
3)以此类推,根据猜测的密钥和式(5)~(10),计算X11其他半字节的值.
对于Step3,只需要猜测sk11,[14:00].与Step2 类似,首先猜测,计算接着猜测,sk11,[14:12], 计算X10每个半字节的值.
Step4, Step5 的过程与Step3 类似.图2 也展示了第9轮利用部分和与密钥搭桥技术恢复X80的过程,即与X9′之 间 的 虚 线 表示:为了计算X80,从第10 轮X9中选取部分状态, 即参与计算.
3.3 复杂度分析
3.1 节的攻击过程的时间复杂度主要来自于Step2~5.
Step2 的时间复杂度约为 260×28+260×24×6次S盒查表;Step3 的时间复杂度约为260×28+260×24×1.75次S 盒查表;Step4 和Step5 的时间复杂度都为260×28+260×24×1.75次 S 盒查表.因此总的时间复杂度为260×28×4/(12×8)≈263.42次12 轮MIBS-64 解密计算.数据复杂度为 260的选择明文.
4 14 轮MIBS-80 的密钥恢复攻击
利用2.2 节中MIBS 的任意一个9 轮积分区分器,在末尾增加5 轮,都能完成一个对14 轮MIBS-80 的密钥恢复攻击.本节以MIBS 所示的一个区分器为例,介绍详细的攻击过程如图3 所示.
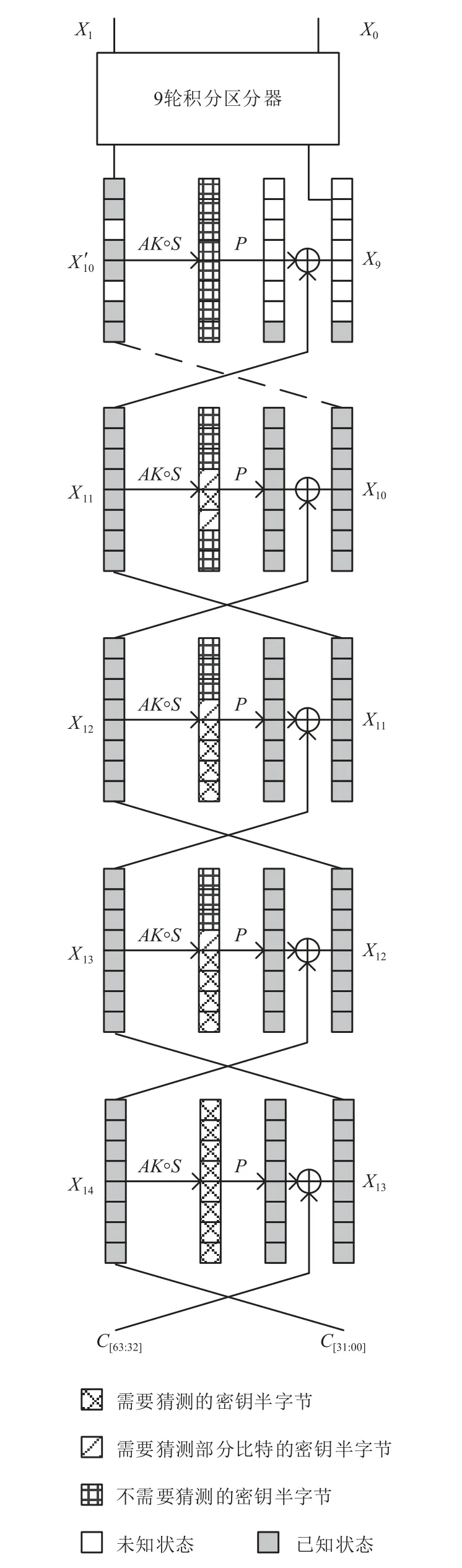
Fig.3 Key recovery attack of MIBS-80图3 MIBS-80 的密钥恢复攻击
4.1 攻击过程
Step1.选择明文集X,X中共有 263个明文,满足明文的第1 个比特为常数,其余比特都是活跃的,查询其14 轮MIBS-80 加密之后的密文C=C[63:32]||C[31:00].
Step2.已知密文C,猜测第14 轮的密钥sk14,解密计算X13=P◦S(C[63:32]⊕sk14)⊕C[31:00].
Step3.猜测第13 轮的轮密钥sk13, 解密计算X12=P◦S(X13⊕sk13)⊕X14.根据性质2,部分密钥比特可以根据sk14,[12:00]直接得到,因此实际只需猜测19 b,即sk13,[18:00].
Step4.猜 测 第12 轮 的 轮 密 钥sk12,解 密 计 算X11=P◦S(X12⊕sk12)⊕X13.根据性质2,部分密钥可以根据sk13,[12:00]直接得到,因此实际只需猜测19 b,即sk12,[18:00].
Step5.猜 测 第11 轮 的 轮 密 钥sk11,解 密 计 算X10=P◦S(X11⊕sk11)⊕X12.根据性质2,部分密钥可以根据13,12 轮的轮密钥得到,实际上只需要猜测10 b,即sk11,[18:09].
Step6.根 据 性 质2,sk10可 由sk11,[12:00]和sk14,[31:04]得到,解密计算X9=P◦S(X10⊕sk10)⊕X11.
Step7.根据定理1,X经9 轮MIBS 加密之后的低32 比特都是平衡比特.因此,满足Xi,9=0的密钥可能为正确密钥.筛选概率为 2-32,共得到232+19+19+10×2-32=248个候选密钥.
4.2 利用密钥搭桥与部分和技术降低复杂度
4.1 节中的攻击过程已经根据密钥桥调整了需要猜测的密钥个数,下面介绍利用部分和技术降低复杂度.
对于Step2,利用部分和技术,逐个计算X13每半字节的值.根据线性变换P,有式(11)(12)成立:
1)根据式(11),计算X103.首先猜测sk104和sk114的值,由于密文已知,解密计算S0(C[031:00]⊕sk014)⊕S1(C[131:00]⊕sk114)出 现的次数;接着猜测sk134,计算第0, 1, 3 个S 盒的求和值出现的次数;以此类推,依次猜测sk414,sk164,sk174, 最终计算得到X103每个可能值出现次数的奇偶性.
2)根据式(12),计算X113.由于在1)中已经猜测了,因此这里只需再猜测sk124和sk154的值.通过猜测的密钥,统计X113每个可能值出现次数的奇偶性.
3)类似于1)和2),根据猜测的密钥及线性变换P计算X13其他半字节的值.
Step3~6 的过程与Step2 类似,区别在于需要猜测的密钥长度小于32 b.
4.3 复杂度分析
4.1 节中的攻击过程的时间复杂度主要来自于Step2~5.Step2 的时间复杂度约为263×28+263×24×6次S 盒查表,Step3 和Step4 的时间复杂度都为263×28+263×24×2.75次S 盒查表,Step5 的时间复杂度约为263×27+263×24×0.75次S 盒查表,因此总的时间约为 263×28×3.5/14×8 ≈266次14 轮的MIBS-80 解密计算,数据复杂度为 263的选择明文.
5 总 结
本文对分组密码算法MIBS 进行了积分分析.对于MIBS-64,在8 轮积分区分器的末尾增加4 轮进行了12 轮MIBS-64 的密钥恢复攻击;对于MIBS-80,在9 轮积分区分器的末尾增加5 轮进行了14 轮MIBS-80 的密钥恢复攻击.在MIBS 的密钥恢复过程中,我们利用密钥搭桥技术与部分和技术,有效地降低了时间复杂度.MIBS 的密钥编排算法比较简单,例如,MIBS-64 的2 轮实际上只用了47 b 互不相关的轮密钥.因此,利用密钥搭桥技术可以极大降低猜测的密钥量.由此可见,轮密钥之间的关系对算法的安全性具有重要的影响.
作者贡献声明:毛永霞提出实验方案并撰写论文;吴文玲提出指导意见并修改论文;张丽负责修改论文.
附录A.S 盒的线性约束条件.
设(a,b,c,d)→(e,f,g,h)表示S 盒的一条可分迹,那么下面的24 个不等式可以充分描述可分性在MIBS 的S 盒上的传播:
附录B.线性变换 P的线性约束条件.
MIBS 的线性变换P对应的矩阵M为
根据矩阵M,以及复制和异或的建模规则,可以直接写出比特级线性约束条件.以第1 行和第1 列为例.设线性变换P的输入可分性 (ai+28,ai+24,ai+20,ai+16,ai+12,ai+8,ai+4,ai), 0 ≤i≤3, 输出可分性(bi+28,bi+24,bi+20,bi+16,bi+12,bi+8,bi+4,bi), 0 ≤i≤3.
遍历i, 0 ≤i≤3, 得到线性变换P最高4 比特输入所对应复制操作的约束条件.同理,遍历所有列,可得到线性变换P所有输入位置对应复制操作的约束条件.
遍历i, 0 ≤i≤3, 得到线性变换P最高4 比特输出所对应异或操作的约束条件.同理,遍历所有行,可得到线性变换P所有输出位置对应异或操作的约束条件.
