考虑瓶颈路段交通流特性的高速公路应急资源双目标调度方法

焦虹桥

(甘肃省兰州高速公路处, 甘肃, 兰州 730030)

0 引言

道路是促进各地交流沟通与发展的纽带,因此道路的修建工作一直是重点工程项目。在一段高速交通公路上,会设置若干个高速公路管理所,每个高速公路管理所都会配备一定的应急资源[1],当高速公路某一处发生交通事故后,管理所会立即将应急资源调度到事故发生点[2]。应急资源调度越及时,发挥的效用越大,越能降低伤亡损失[3]。在此背景下,进行高速公路应急资源调度方案研究是十分必要的,但结合我国东西部差距可以明确,不同地区交通流调度方案存在一定差异性。东部地区人口众多、城市化水平高、交通需求量大,因此交通基础设施相对完善。西部地区资源丰富,具有一定的经济发展潜力,但交通网络仍存在区域连接性较差的问题。因此,东部地区的交通流调度方案更侧重解决城市交通拥堵问题和提高交通效率,而西部地区的交通流调度方案则需着重加强基础设施建设和提升区域连接性。

在上述背景下,张伟等[4]利用累计频率曲线法对事故发生概率以及严重程度进行了预测,并以此为基础建立了双目标优化调度模型,通过LINGO求解器求解得出应急资源调度方案。黄彩霞等[5]对调度问题进行了描述,建立了运输消耗成本最低、装车时间最少的双目标函数,在8个约束条件下,通过改进飞蛾扑火算法求取同时满足2个目标的调度方案。张莉等[6]通过熵权法计算了需求点的紧迫度权重,让权重最大值的需求点享有优先配送权,以配送路径最短为目标,利用改进粒子群算法求取资源调度方案。SOMY等[7]基于超级网络理论提出了一种区域应急调度方法,在考虑应急物流供应链的基础上,利用改进投影算法将应急调度问题转化为线性不等式求解问题,提出了应急资源综合性调度方案。

针对没有考虑瓶颈路段交通流特性,导致应急资源送达延误的情况,本文研究一种考虑瓶颈路段交通流特性的高速公路应急资源双目标调度方法。

1 瓶颈路段交通流特性分析

结合突变理论对瓶颈路段交通流特性进行研究,选取速度、密度、流量3个可以代表交通流特性的变量[8],并将所取变量分别对应尖点突变理论模型中的基本参数,对应速度参数可得到状态变量x,对应密度参数可得到控制变量y,对应流量参数可得到控制变量z。若将上述变量的坐标点位置进行变换,即:

(1)

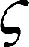
(2)

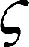
(3)

(4)

式中,Ri代表第i个区间数据点。将去除离群点后的剩余数据重新进行降序排序,得出突变区间内速度标准范围,然后代入奇点集方程,确定密度标准。根据上述研究成果,对瓶颈路段交通流特性进行划分,具体如表1所示。当已知某一时刻瓶颈路段的行车速度和车辆密度,就可以确定当下时刻该路段的交通流特性。

表1 瓶颈路段交通流特性划分标准表

2 高速公路应急资源双目标模型

为了方便建立模型的操作需要,需要给出几点假设条件,具体如下:

1) 已知所有需要救援的事故发生点的地理坐标;

2) 已知应急资源所在的高速公路管理所的地理坐标;

3) 已知事故发生点所需要的资源种类及数量;

4) 调度不会受到考虑天气、车辆本身状况、道路受损等因素的影响;

5) 所有救援车辆所承载的最大资源量是相同的;

6) 救援车辆的目标行驶速度为固定值;

7) 每个高速公路管理所可以为大于等于1个事故发生点服务;

8) 根据实际情况,每个高速公路管理所调度的车辆数量不定,不必全部派出,但同时派遣车辆数量不超过所拥有车辆数量最大值。

为此,在这里设置两个目标函数,即路径最短和时间最少,只有同时满足这两个目标的调度方案才是最合理的。

目标函数1:路径最短。

(5)

目标函数2:时间最少。

(6)

其中,

(7)

(8)

(9)

(10)

式(5)～式(10)中,Dmin代表路径最短,dij代表从高速公路管理所i到第j个事故发生点的距离,gkij代表决策变量,取值1或者0,xij代表决策变量,取值1或者0,取值1或者0,r代表瓶颈路段交通流特性,取值1、2、3,Tmin代表时间最少函数,tij代表从高速公路管理所i到第j个事故发生点的所需时间,aij代表决策变量,取值1或者0,cj代表发生事故的概率,bij代表从高速公路管理所i到第j个事故发生点的交通阻抗,n代表高速公路管理所数量,m代表事故发生点数量,K代表应急救援车辆数量。

将目标函数1与目标函数2组合在一起,构成双目标函数并为其设置约束条件。

(11)

s.t.

(12)

式中,lij代表高速公路管理所i向第j个事故发生点提供的资源量,Qi代表高速公路管理所i的资源储备量。

参照上述双目标函数求出的方案既保证了路径最短,也保证了时间最少,极大避免了瓶颈路段交通流状态对应急救援的干扰。若在紧急情况下,需要专注于解决某一具体目标进行调度处理,则需要考虑调度资源的限制,将双目标函数转变为单目标函数,更具有针对性地解决应急需求。

可以根据紧急情况的具体要求,重新处理和选取与瓶颈路段交通流特性相关的数据作为单目标优化的重点,如最小化瓶颈路段的平均交通流延误时间,或最大化疏散车辆的速度等,以此构建单目标函数,并设置适用于单目标优化的约束条件。

3 高速公路应急资源调度方案求解

为了求解双目标函数,得到满足双目标函数的高速公路应急资源调度方案,引入一种寻优算法,即混合蛙跳算法,求解过程如下。

首先初始化青蛙种群,也就是将所有可行的调度方案作为初始可行解,可行解可由青蛙种群中的个体位置表示。再针对个体位置数据进行编码,以此得到个体适应度值,适应度值通过本文构建的双目标函数来计算,该双目标函数在混合蛙跳算法被称为适应度函数。将计算结果记为z1,z2,…,zM,并按数值大小进行排列,将数值最大的参数排列在前,记录该参数对应的青蛙位置,再按由大至小的顺序进行排列。接下来,对青蛙进行分组。将M只青蛙分为N组,每组中要求有n只青蛙,分组规则如第1只分给第1组,第2只分给第2组,以此类推至第n只分给第N组终止,并将推算结果代入第1组,即第n+1只分给第1组。按上述方法进行循环分组,直到最后1只青蛙分组完成后,停止分组。接着在每组中进行内部寻优,将所设定的目标位置作为参考,并将所有青蛙的位置向参考数据靠拢。具体过程如下。

1) 令TN=0,TN取值0～N之间,与分组数量相等。

2) 令TN=TN+1。

3) 令Tp=0,Tp表示进化次数,P代表每组允许进化的最大次数。

4) 令Tp=Tp+1。

5)h1表示组内位置最好的青蛙;h2表示组内位置最坏的青蛙;h3表示族群整体中位置最好的青蛙。

6) 由式(13)更新h2:

(13)

式中,V代表调整矢量。

7) 判断新的h2是否比原来的好。若否,h1代替h2,由式(13)产生新的h2;否则,进入步骤9;

8) 判断新的h2是否比原来的好?若否,随机产生新的h2;否则,进入步骤9;

9) 新的h2代替原来的h2。

10)Tp是否等于P?若否,回到步骤4);若是,进入步骤11);

11)TN是否等于N?若否,回到步骤2);若是,结束内部寻优。

将完成上述过程的N个群体再次混合在一起并重新通过降序找到最优个体,接着循环执行上述分组以及内部寻优过程,直至达到结束条件,输出最优的高速公路应急资源调度方案。

4 方法测试与分析

4.1 研究区概况

以某区域为例,该区域内分布了3个高速公路管理所(见图1),每个高速公路管理所拥有5辆应急救援车,每辆应急救援车能够承载10份应急资源,以应对该区域内高速公路上所发生的交通事故。

图1 某区域高速公路干线图

4.2 瓶颈路段交通流特性

针对图1中瓶颈路段,采集该路段高速公路24 h的速度与密度数据,对比表1可得出每段高速公路瓶颈路段交通流特性,结果如图2所示。

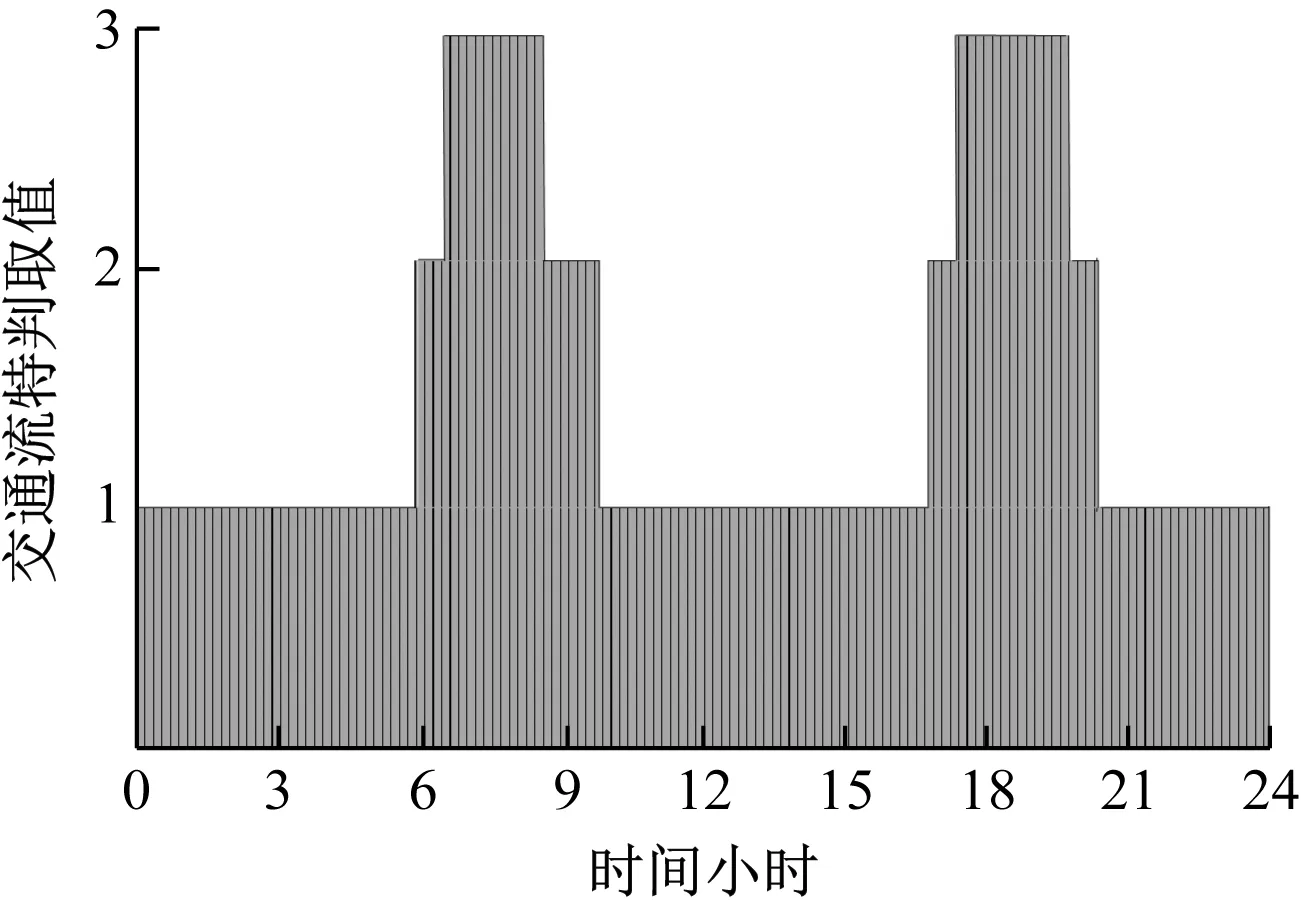
图2 瓶颈路段交通流特性注:交通流特性判别取值具体见式(10)

从图2可以看出,瓶颈路段在不同时间段呈现出不同的交通流特征。假设交通事故发生在与这3个交通流特征相对应的时间段内,以此设计调度计划。

4.3 调度方案

假设图1研究区内有5处发生事故,利用混合蛙跳算法求取瓶颈路段3种交通流特性下的调度方案,结果如图3所示。

(a) 自由流

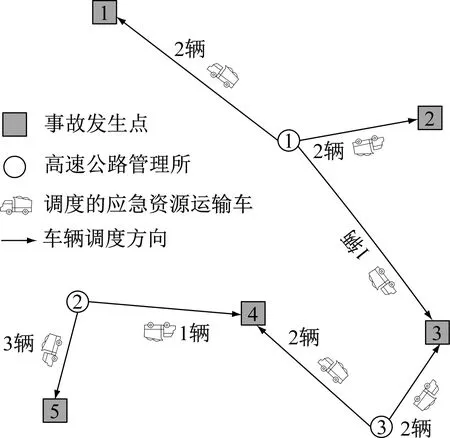
(b) 混沌流

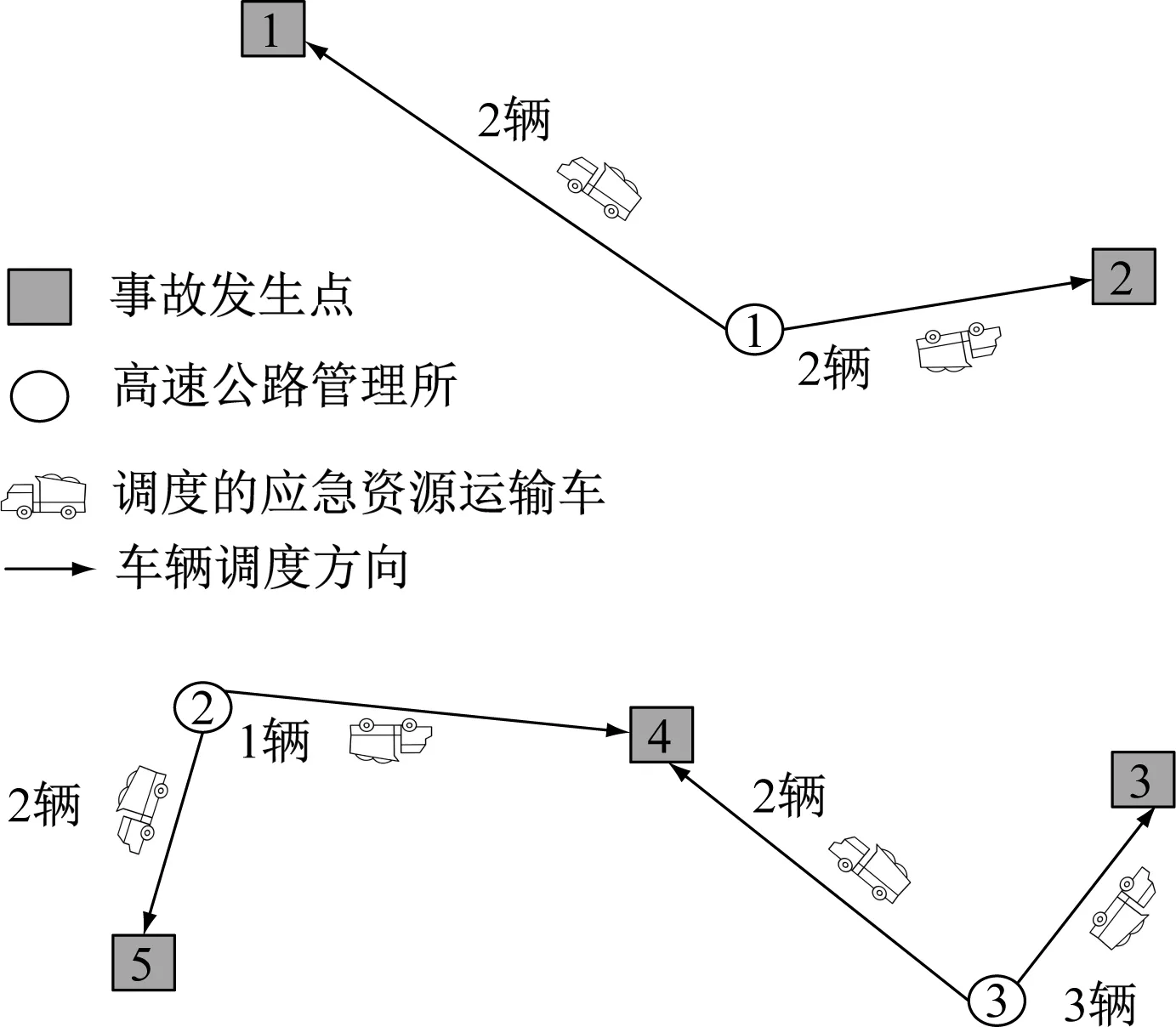
(c) 拥堵流图3 应急资源调度方案

4.4 调度方法性能比较分析

为保证测试过程稳定,提高测试结果的比较性,首先将测试条件进行统一,然后利用LINGO求解器、改进飞蛾扑火算法、改进粒子群算法进行求解。根据结果可得出三种对比调度方案,再结合混合蛙跳算法求出的调度方法,利用VISSIM仿真平台进行仿真应用,统计每种调度方案的路径总长度和所用总时间,结果如表2所示。

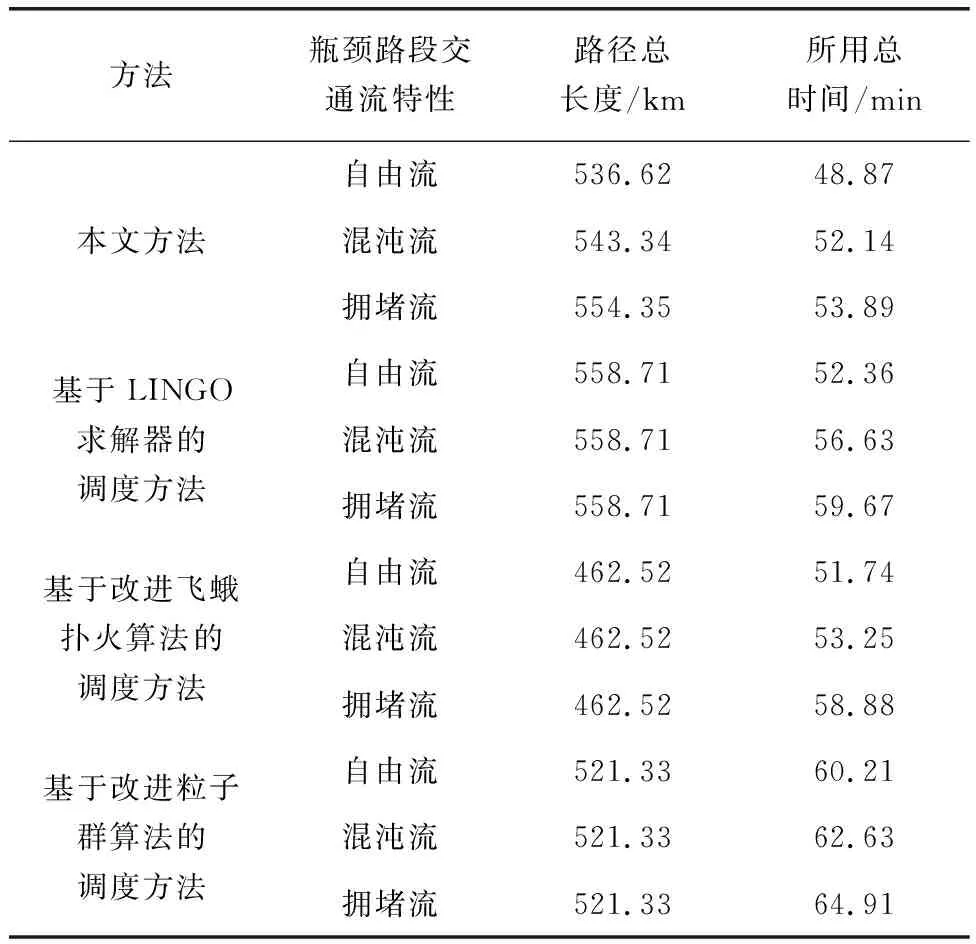
表2 调度方案路径总长度和所用总时间比较结果

从表2中可以看出,与利用LINGO求解器、改进飞蛾扑火算法、改进粒子群算法求解的调度方案相比,本文方法求解的调度方案路径总长度不是4种调度方案中最短的,也不是最长的,但所用总时间是最少的。二者综合来看,再加上应急资源调度时间的及时性要求,本文方法求得的调度方案最为合理,具有较好的实际应用效果,证明了本文方法的有效性。

5 总结

为了能够及时实施救援,减少伤亡和损失,在每个高速公路管理所都会配备应急资源。在此情况下,如何将应急资源快速调度到事故发生点成为本文研究的重点。为此,本文提出一种考虑瓶颈路段交通流特性的高速公路应急资源双目标调度方法,该方法以瓶颈路段交通流特性为前提条件下,求取了不同特性下的调度方案。对本文方法进行应用测试,通过比较分析不同方案的路径总长度和所用总时间,证明了本文方法的有效性。