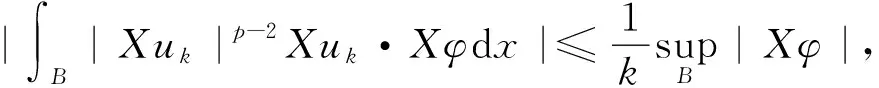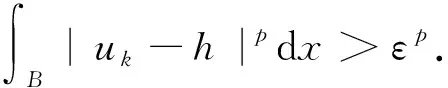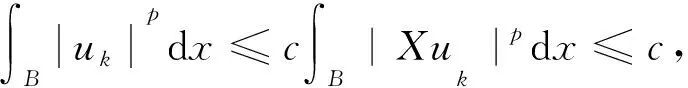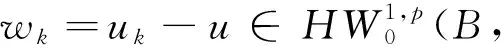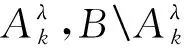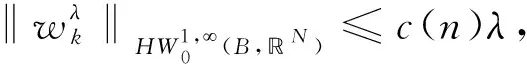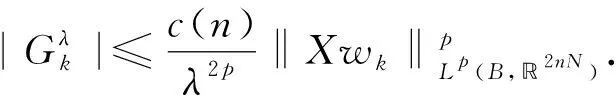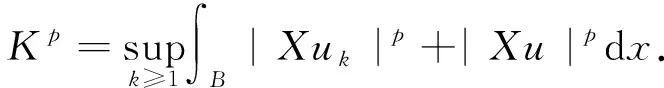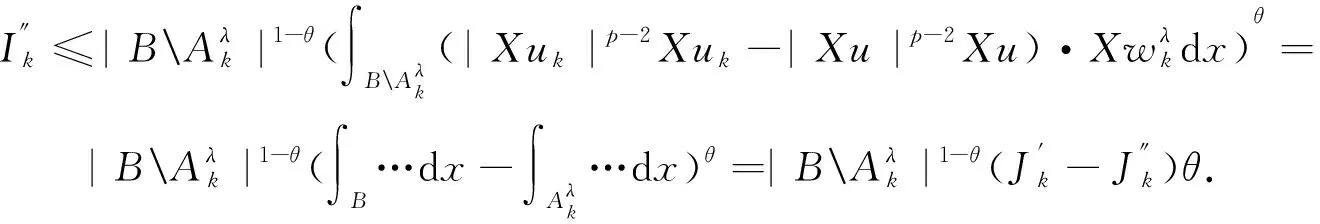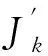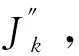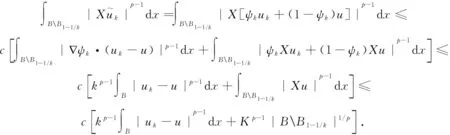关于Heisenberg群上的p-调和逼近定理*
2023-12-13胡紫婷王家林
胡紫婷,王家林,
(赣南师范大学 数学与计算机科学学院,江西 赣州 341000)
0 引言和主要结果

是Xi的伴随矩阵.
近年来,关于Heisenberg群上退化次椭圆p-Laplace方程弱解的正则性研究已取得丰富的成果,见文献[1-4]及其参考文献. 然而,关于Heisenberg群上退化次椭圆p-Laplace方程组的正则性研究较少见,最近,Zheng和Feng在文献[5]中研究了Carnot群上一类次椭圆p-Laplace方程组,建立了p仅在2附近取值时弱解的Hölder连续性,p在其它区间取值时,尚无结果,主要的困难是缺乏一个有效的工具来解决Heisenberg群上水平向量场的非交换性以及次椭圆p-Laplace算子的退化性等问题. 早在2005年,Duzzar和Mingione在文献[6]中研究了欧氏空间的p-调和映射,通过p-调和逼近技巧导出衰减估计并建立了其弱解的C1,α正则性,可见p-调和逼近理论对弱解的正则性研究是一个十分有效的工具.为此,本文在Heisenberg群上建立相应的p-调和逼近定理,这对进一步研究Heisenberg群上退化次椭圆p-Laplace方程组弱解的正则性起着重要作用.
本文的主要结果如下:
定理1设
若对于任意ε>0,都存在一个正常数δ(n,N,p,ε)∈(0,1]有

(1)
时,则存在p-调和函数h∈HW1,p(Ω,N),使得
1 Heisenberg群基础知识
Heisenberg群Hn=2n+1定义群乘法为:其中x=(x1,t)=(x1,…,xn,y1,…,yn,t),y=(y1,v)=(xi+1,…,xi+n,yi+1,…,yi+n,v).零元素为(0,0),并且(x,t)的逆元为(-x,-t),其相应Lie代数的一组基向量场为:关于Lie括号满足:[Xi,Xn+i]=-[Xn+i,Xi]=T,[Xi,Xj]=0和[T,T]=[T,Xi]=0,其中矢量X被称为水平梯度,T被称为垂直导数.


定义1设f是Rn上的局部可积函数,则极大函数f可被定义为:M(f)(x)=sup{∮B(x,r)f(y)dy∶r>0}.
2 相关引理
本节重点引入一些与向量场相关的基本引理.首先回顾Sobolev嵌入不等式和Poincaré型不等式,具体证明参考文献Garofalo-Nhieu[7], Lu[8]和Nagel-Stein-Wainger [9].
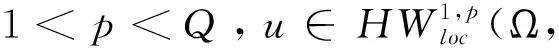
‖u-ux,R‖Lq≤C‖Xu‖Lp,
(2)




(3)
其中当1 引理4[12]设f∈Lp(Rn),1 ‖M(f)‖p≤C‖f‖p. (4) 下面,利用文献[13]的思想,在Heisenberg群上建立如下结果. 引理5在HW1,p(Ω,N)中,当wk弱收敛到0时,存在正常数c=c(n,p),对于任意λ>0,都有序列N),使得 (5) (6) 且有 (7) 证明在这里,假设 利用Hölder不等式和引理4可得 即得 根据极大函数的定义和范数有界这个性质,有 眼下,系统正考虑接入前期预算立项环节管理,以及后端合同执行、评价、监管、考核两部分内容,以实现采购全流程线上管理。 下面来证明(5)式,由HW1,p(Ω,N)的范数定义和Sobleve嵌入不等式可得 其中0<ρ (8) 同理可得 (9) (10) (11) 利用文献[13]中的命题4.4的思想,建立引理6. 引理6设ε>0,存在一个子序列{uk}k∈κ,κ⊂,使得对于任意k∈κ有 (12) 证明令ε∈(0,1),存在N∈使得 Nε>K, (13) 其中K和(11)式中的K一致. 定理1的证明在y→u(ρy)映射里,令ρ=1,此时Bρ=B1,下面简记为B.应用反证法的思想,假设存在ε>0和序列{uk}∈HW1,p(B,N),使得对于所有的N)满足 (14) 和 (15) 则对任意的k和任意的p-调和函数h∈HW1,p(B,N),满足 (16) 和 (17) (18) (19) 在B上几乎处处有uk→u, (20) (21) 下面将证明存在一个子序列(无限集)κ2⊂,使得 (22) 对任意的k∈,又设 (23) 情形1先给出在(23)式的假设条件下建立(22)式. (24) (25) (26) (27) 估计 (28) 根据引理5可知 (29) (30) (31) 这里记 (32) (33) (34) (35) 对(35)式最后一行左端第一项应用Hölder不等式,(24)和(30)可得 (36) 同样地,对(35)式最后一行右端第二项应用Hölder不等式,(24)和(29)式得 (37) 由(35)-(37)式可得 (38) 结合(33),(34)和(38)式推出 (39) (40) 其中常数c=c(n,p)≥1. 现在证明 |G|≤2cKpλ-p, (41) (42) (43) 由于当ε→0时,(43)式右手边的量也趋于0并且ε>0可以取到任意小,所以可以应用(37)-(43)式中描述的参数,从整个序列开始(即取κ0=),并执行标准对角参数得到进一步的子序列κ2⊂使得也就是说,在L1(B)上,当κ2k→∞时,有[(|Xuk|p-2Xuk-|Xu|p-2Xu)·(Xuk-Xu)]θ→0,因此,可以假设当κ2k→∞时,在B上几乎处处有(|Xuk|p-2Xuk-|Xu|p-2Xu)·(Xuk-Xu)→0;特别地,这一事实和(3)式的单调性可以表明,在B上,当κ2k→∞时,有Xuk→Xu.因此,在(23)的假设下证明了(22). 情形2现在考虑一般情况,在没有(23)式的假设下建立(22).注意到(19)式的强收敛,可设子序列满足 (44) (45) 结合前面的估计可得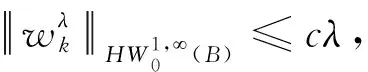













3 主要结果的证明