基于DGS的电磁交叉耦合微波带通滤波器*

2023-12-13张梦璐荣垂才孙鑫营

赣南师范大学学报 2023年6期

徐贇,张梦璐,荣垂才,孙鑫营

(赣南师范大学物理与电子信息学院,江西赣州 341000)

目前,现代无线通信正处于一个高速发展的时期,随着市场对通信产品需求的不断增加,“频谱拥挤”现象也日益突出.为了保证各个频道间良好的通信质量,一款性能优良、尺寸小,成本低的滤波器显得尤为重要.传统滤波器设计常用提高滤波器阶数来提高通带选择性,但这种方法极不利于滤波器小型化,同时也恶化了群延时.交叉耦合滤波器具有高选择性,低插损,宽阻带等优势,基于广义切比雪夫函数[1],通过交叉耦合可灵活引入传输零点来增强滤波器的频带选择性.缺陷地结构(Defected Ground Structure,DGS)是在接地平面上蚀刻周期性或非周期性的平面结构,接地层中的屏蔽电流会影响微带线的电感和电容,从而在某些频率下产生谐振,利用此特性可以达到抑制谐波的目的[2].

图1 电感、电容耦合结构原理图与S参数图

本文基于交叉耦合理论[3],采用内折叠微带开口环谐振器为基本谐振结构,同时加载缺陷地结构,设计了一款中心频率为3.35 GHz,带宽300 MHz的微带带通滤波器.测试结果表明,通带内S21≥-3.1 dB,S11≤-15 dB,群时延1.4 ns～1.88 ns.

1 耦合原理与结构

1.1 电耦合与磁耦合

耦合泛指能量的传递与交换,电耦合与磁耦合的区分主要在于两个谐振腔之间能量交换方式取决于电场或磁场[4].关于场的表达终究是复杂的,可简化为电路原理图的形式,即用电容耦合表征电耦合,用电感耦合表征磁耦合,原理图与仿真S参数如图1所示.

由图1可知,无论是电感耦合还是电容耦合其S11与S21都存在一个90°的相位差,但是两者的区别在于,当电感耦合时S11相位接近于0,S21相位超前于S11相位90°;当电容耦合时S21相位接近于0,S21相位滞后于S11相位90°.故磁耦合也被称之正耦合,电耦合被称之负耦合.

1.2 交叉耦合理论

在一个交叉耦合谐振器滤波器模型中,两个或多个谐振器之间相互作用,进行原理分析时可用L-C等效电路代替单个谐振器单元[5].根据不同耦合结构拓扑,可得不同谐振器之间的耦合关系;一般分为直接耦合与间接耦合,通常相邻两个谐振器之间称为直接耦合,两个非相邻谐振器之间称为间接耦合.其交叉耦合带通滤波器等效电路如图2所示.

图2 交叉耦合带通滤波器原理图

由图2可知,根据基尔霍夫电压定律,任一闭合回路的电压代数和为零;可得其回路方程为[6]:

[ωU-jR+M][I]=[Z][I]=-j[e]

(1)

式中:ω为归一化低通原型角频率;j为虚数单位;U为N×N单位矩阵;R除第1行第1列为R1和第N行第N列为R2外,其余元素均为零;M为归一化N×N耦合矩阵;Z为等效的阻抗矩阵;I为电流向量,由各个谐振回路电流构成的N阶向量;e为滤波器激励向量,且e=[1,0,…,0]T.根据式(1)可得:

[I]= -j[Z-1][e]

(2)

可推出散射参数方程为[7]:

S11=1+2jR1[Z-1]11

(3)

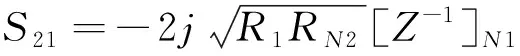
(4)

基于式(3)和式(4)可建立起广义切比雪夫函数与交叉耦合滤波器等效电路的联系,后续可利用MATLAB等数据处理软件对交叉耦合滤波器的耦合矩阵进行提取与优化.

1.3 谐振器结构分析

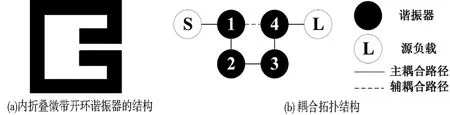
图3 单个谐振器与滤波器耦合结构拓扑图

本文利用内折叠微带开口环谐振器,基于交叉耦合理论,对一款工作于S波段的滤波器进行仿真设计.图3(a)是内折叠型微带开口环谐振器的结构,(b)是相应的耦合拓扑结构.

根据开环谐振器的场分布可知,谐振时,在谐振器的开口处电场最强,而相对的微带线中间磁场最强[8].由于谐振器之间都是通过边缘场进行耦合的,而微带线的边缘场会出现阻尼衰减特征,可根据谐振器之间距离与相对偏移量来调整对应的耦合系数.内折叠开环谐振器是在普通开环谐振器的基础上增加了两个朝内的折叠枝节,新增一个内耦合,可在更小的尺寸下,实现谐振器之间耦合度更加灵活的调节,进一步有利于滤波器小型化设计.当两个谐振器开口相对排放时,耦合位于电场最强处,此时形成较强的电耦合; 当两谐振器开口相背离排放时,耦合位于磁场最强处,故为磁耦合;当两种耦合同时存在时,称为混合耦合.图3(b)中,谐振器1和4之间是电耦合,谐振器2和3之间是磁耦合,输入信号分别经过1-2-3-4以及1-4两条路径传输并在输出端汇合,两条路径相位相差180°,所以会在有限频率上产生一对传输零点,从而有效地改善了滤波器选择性.

1.4 DGS结构分析

DGS结构最初是由光学领域中的PBG(Photonic Band Gap)演变而来,由于导地金属板完整性被破坏,从而影响接地板上传导电流的分布.DGS结构进行原理分析时可用一个简单的LC并联电路来等效.图4为DGS等效电路模型.

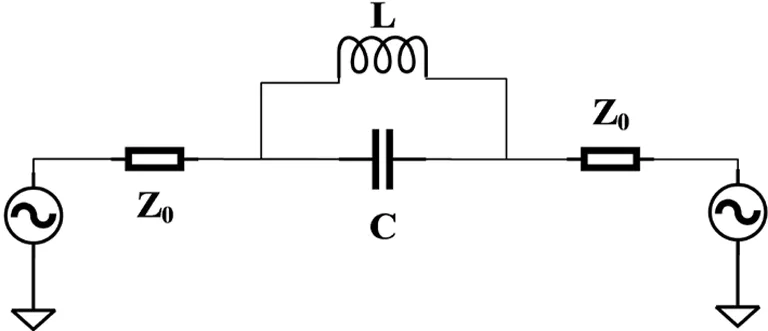
图4 DGS单元等效电路

图4中等效电路参数可由式(5)和式(6)计算得出.其中代表 LC并联谐振电路的谐振频率,即衰减极点所在的频率;代表3 dB截止频率.

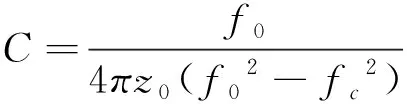
(5)

(6)

2 滤波器设计

2.1 设计指标

为满足S波段通信的需求,同时保证滤波器传输效率达95%以上,具备一定的抗干扰能力,结合实际项目应用确定指标为:

2.2 滤波器耦合矩阵的提取

根据设计要求,可以综合出符合要求的耦合矩阵M[9].滤波器设计中,通常需要将带宽进行一定增大,还要考虑到边带衰减与实物的频偏,因此将带宽扩大为3.175 GHz～3.525 GHz,此时计算相对带宽为10.45%.综上可得耦合矩阵M为:

2.3 馈电设计

图5 馈线结构

微带滤波器的馈电方式主要分为直接馈电和间接馈电两类[10].其中后者电路结构尺寸比较大,且对于耦合缝隙距离的调整较为繁琐,过宽容易造成外部Q值过大,较窄时受限于加工精度影响.采用直接馈电的方式,具体馈线结构如图5所示.馈线直接与开口环谐振器相连,通过调节馈线的尺寸与谐振器之间的相对位置,可得到理想的Q值.

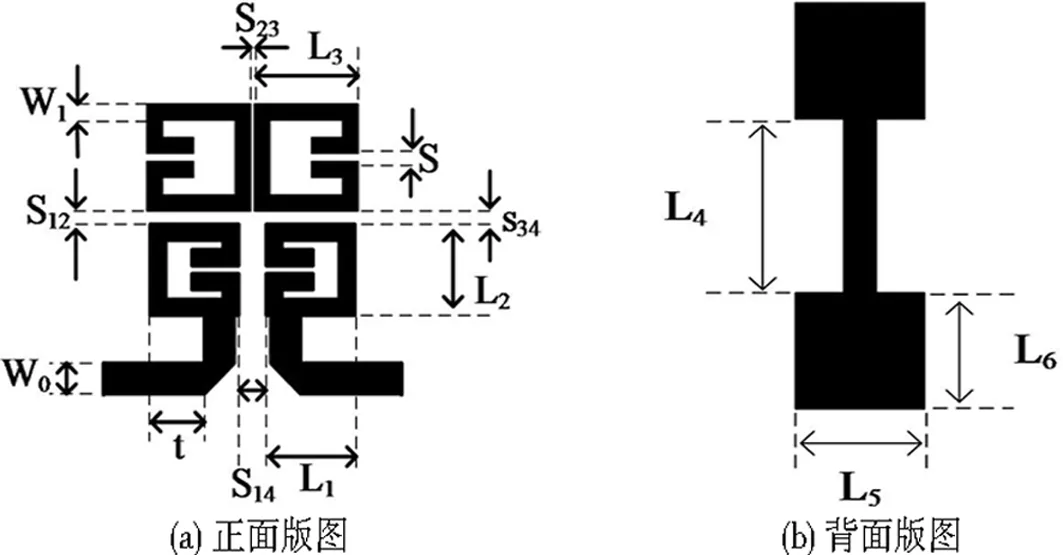
图6 滤波器版图

由图5可知,由于元件尺寸限制,故对馈线做了一个折叠处理,并在其拐角处进行了一个45°外斜切处理,其主要目的是为了增大拐弯处特征阻抗,降低拐弯处的不连续影响.

2.4 耦合系数的提取

该滤波器存在多种耦合方式,在HFSS 15.0建立了各个谐振器之间的全波仿真模型.借助耦合矩阵M,得到谐振器之间距离.文献[11]详细讲述了关于外部Q值与耦合系数的提取方法,图6为滤波器版图.

根据文献[12]中,加载DGS结构能达到抑制谐波分量的目的,在滤波器背部加载了一个哑铃型DGS结构,其版图如图6(b)所示.滤波器初始的物理尺寸可通过HFSS仿真,基于耦合系数K与外部品质因数Q来确定,然后再进一步分析仿真结果,逐步优化得到符合设计要求的尺寸.表1为优化后的物理尺寸.

表1 滤波器物理尺寸 mm

2.5 滤波器测试结果

滤波器整体EM仿真基于HFSS 15.0完成,版图采用介电常数为4.4的FR4板材,厚度为1 mm,滤波器整体尺寸为24.0 mm×19.2 mm.图7为滤波器实物与测试滤波器特性.

图7 滤波器实物与测试结果

表2 相关滤波器性能对比

1Insertion Loss,2Return Loss,3Functional Band Width,4Group Delay

由图7(c)、(d)可知,通带内群时延为1.4 ns～1.88 ns,两个传输零点位置发生改变,带外抑制效果优于仿真结果,实际滤波器中心频率为3.35 GHz,通带3.2-3.5 GHZ,插入损耗约为-2.4 ～ -3.1 dB,波动小于0.7 dB,回波损耗小于-15 dB,2.8 GHz插损小于-40 dB,4-5 GHz插损小于-30 dB.综上所述,所有指标均符合设计要求,同时还具有带外抑制良好、结构紧凑、成本低等优势.表2为本文滤波器与已发表论文的性能对比.