车载电池包动力学建模方法与影响因素研究

梁新龙，方有为，张 龙，吕希祥

车载电池包动力学建模方法与影响因素研究

梁新龙，方有为，张 龙，吕希祥

（合肥国轩高科动力能源有限公司，安徽 合肥 230011）

电池包是一个包含机-电-热多部件的复杂综合体，开展机械性能分析较为困难，同时给后续对标带来了较大挑战，因此合理建模方式显得尤为重要。文章采用均质化的模型等效方法及精细的前处理，结合压缩试验方法获得的各向同性材料性能数据，对电池系统及其零部件分别开展模态仿真，结合扫频测试数据，验证了模型的有效性和精度；通过试验与仿真的对标验证了电芯与支撑泡棉的材料数据，对比有无泡棉和有无箱盖的扫频试验数据，获得了箱盖和支撑泡棉对系统刚度的影响规律，并解释了几种状态扫频曲线差异性的影响因素及原因。

动力电池包；模态分析；扫频测试；阻尼系数

随着环境污染和能源短缺问题日益严峻，新能源汽车的研发成为汽车行业的发展重心[1]。动力电池作为其关键技术之一，将直接影响车辆的续航里程与行驶安全，而承载电池模组的电池包是电动汽车的关键安全部件[2]，因此，针对电池系统可靠性研究是新能源汽车主动安全的核心问题。陈雨等[3]通过对包内电池单元动力学精确建模，使电池包系统模态仿真结果相对误差控制在5%以内。同时，结合电池包系统模态也可以来验证电池包内部各零部件的刚强度[4]。新能源行业的快速发展，意味着试验设备测试资源的需求也在大量增加，在设计开发阶段运用计算机辅助工程（Com- puter Aided Engineering, CAE）技术开展虚拟验证工作，尤其是在提升设计质量和水平，减少测试成本，缩短开发周期等方面表现出巨大优势。

电池系统作为一个包含机-电-热多部件的复杂系统，它的整体刚度影响着电池系统的安全与可靠性[5]，甚至影响整车的噪声、振动、声振粗糙度（Noise, Vibration, Harshness, NVH）性能，长期的项目经验表明，电池系统的各个零部件对系统刚度都会产生不同程度的影响，如箱盖、底护板、支撑泡棉等零件对系统刚度的影响研究，尚未在公开文献中发表。尤其是箱盖不仅需要满足密封的要求，还要具有一定的刚度，满足扭转弯曲刚度及掌压刚度的要求，避免在整车行驶过程中产生振动噪声与异响。

1 建模思路与方法

任何复杂动力学模型都可以通过简化的方式等效，电池包中电芯不仅是一种各种材料组成的复合结构，而且还是一种高度非线性结构，本文采用均质化方法模拟电芯。电池系统在装配时使用大量螺栓，螺栓定扭后螺柱会产生预紧力，而预紧力使得组合结构在装配完成时存在预应力场，预应力场会影响整个装配体的固有频率，有研究表明由预紧力导致的频率变化在误差允许的范围内[6-7]，本文不考虑预紧力对结构动刚度的影响，各紧固件通过刚性单元连接等效。

各个组件之间需要定义接触关系，存在边界非线性。研究表明，当接触状态趋于稳定，则结构刚度矩阵不再变化，可以近似为线性结构而采用线性计算。自由度无阻尼或比例阻尼的线性系统的固有振动方程为[8]

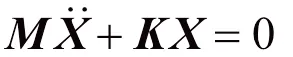
设主振动为

=sin(+) （2）

式中，为常数列矢量。

=(12,...,ϕ)T（3）

将式（3）代入式（2），得到下列代数齐次方程组：

(-2)=0 （4）

式（4）存在非零解的充要条件是行列式为零，即得到不考虑预应力场的特征方程

|-2|=0 （5）

求解关于2的次多项式，获得系统第阶固有频率ω，最终求得系统第阶固有振型φ。由式（5）可知，系统固有频率由系统刚度和质量共同决定，而刚度包括材料刚度和结构刚度，所以提升固有频率方法包括更换弹性模量更大的材料、提升零件截面模量、降低系统质量。

电池包仿真分析流程包括三维模型输入、简化模型及处理、网格划分、网格质量检查、搭建有限元模型、数值求解计算、计算收敛、后处理、结构优化等。完整的电池系统包括下壳体、上壳体、支撑泡棉、模组或电芯、固定拉杆、横纵梁、安装支架、液冷板、导热胶、各种电气件、线束、接插件、螺钉等。建模前处理时应保留核心结构部件，不宜保留非核心结构件，箱体及电气件支架的建模要求：1）应能正确反映部件的特性及运动关系；2）CAE模型重量应与实际电池包重量相等（内部零件可用质量点代替）；3）CAE模型的重心坐标应与三维数模重心坐标相同；4）通常忽略三维数模的局部特征（如散热孔、工艺孔、倒角等），保留外部轮廓和安装孔。

2 数值模型的建立

为改善电池包在振动测试及实际使用情况的NVH性能，常用的手段之一就是在箱盖内表面或模组的上表面粘贴缓冲泡棉[9]并设计有一定的压缩量，保证泡棉对箱盖支撑作用，提高箱盖弯曲扭转刚度和掌压刚度。泡棉是一种超弹性材料，为研究泡棉对系统响应的影响，本文选取A和B两款电池包开展有无泡棉及有无箱盖对系统响应的试验设计，共设计三组试验。

为研究系统箱盖及其泡棉对系统响应的影响，本文选取两个典型项目开展仿真与计算对标研究，在有限元仿真软件HyperMesh中建立有限元模型，长厚比≥10的结构采用壳网格的方式离散，对长厚比＜10的结构采用实体单元离散，其中的螺栓连接通过在螺栓孔周围需建立Washer，相邻两零件的Washer单元直接使用Rbe2连接；焊接连接通过在两零件之间建立一层六面体单元，六面体单元两侧的节点通过Rbe3单元和对应的零件连接到一起。

在进行电池包整包机械性能分析时，往往需要考虑箱盖，由于单独箱盖的刚度较差，箱盖中间区域与箱体需要建立支撑，而工程实践中常用的方法就是在模组上表面或箱盖内表面粘贴泡棉，箱盖螺栓孔与箱体螺栓孔之间通过Rbe2刚性单元连接。

电池系统有限元模型如图1所示，本文研究的A、B两款电池包箱盖都是钢材DC06，箱盖内表面设计有相同的缓冲泡棉，模组均使用塑料端板的铁锂电芯，模组尺寸规格相同，箱体四周设置固定点；不同之处在于箱体材质不同，A项目使用铝型材，B项目使用钢钣金，其次是箱盖刚度不一样，本文为研究箱盖刚度和泡棉对系统动态响应影响，特选择两种材料相同刚度不同的箱盖，因为相同尺寸规格的箱盖如材质相同，其箱盖自身刚度基本相同，无法体现不同刚度对系统刚度影响。

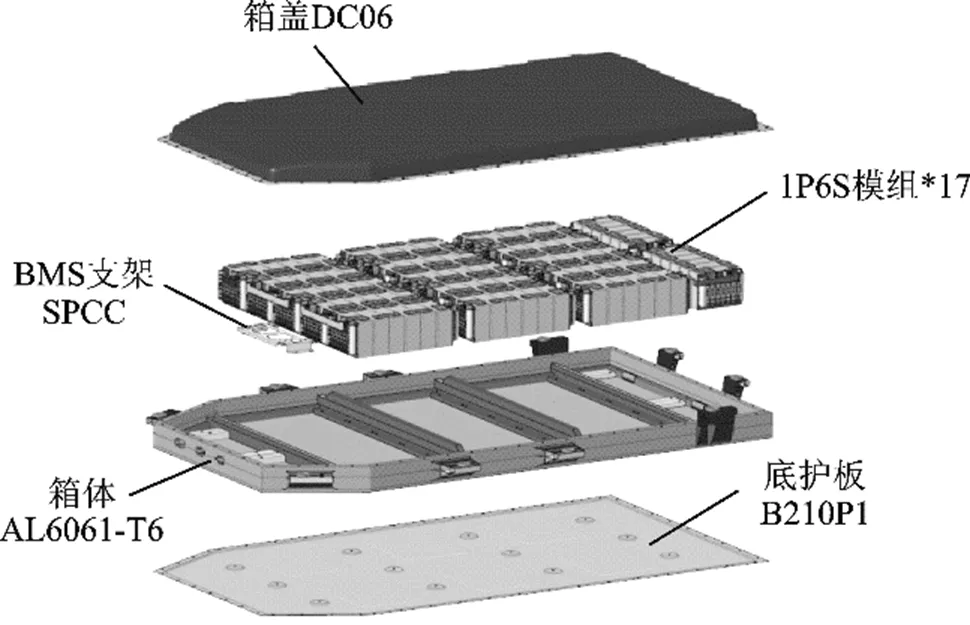
(a) A项目电池系统有限元模型

(b) B项目电池系统有限元模型

图1 电池系统有限元模型

根据泡棉不同弹性模量对结果的影响，根据对标结果最终确定泡棉的弹性模量为0.35 MPa，这与试验测试得到的泡棉压缩模量0.38 MPa是一致的，首先泡棉进行压缩试验，得到泡棉材料的应力应变曲线，然后根据应力应变曲线中线性阶段斜率值0.38得到泡棉的弹性模量，采用和泡棉同样的测试原理等效出电芯的弹性模量为75 MPa。

3 结果与讨论

3.1 A项目仿真试验对标

针对三种状态的系统分别进行了模态分析，根据输出结果文件中的质量参与系数，得到了箱盖和三种状态电池包的一阶固有频率，如图2所示，计算结果如表1所示。

由表2可知，当支架工作阻力为p时，工作面顶板下沉量Δh2=600 mm，控顶效果为“差”；当支架工作阻力为p、p1时，工作面顶板下沉量分别为Δh1=365 mm和Δh3=456 mm，控顶效果为“中”，当支架工作阻力为p2时，工作面顶板下沉量为Δh4=294 mm，控顶效果为“好”。比较控顶效果，支架工作阻力为额定工作阻力p、来压支架均值上阻力p2时，顶板下沉量分别为365、294 mm，区别不大。

(a) 箱盖模特分析阵型图

(b)系统模特分析阵型图

图2 箱盖及电池系统阵型图

表1 三种状态电池系统模态分析结果汇总 方案状态系统一阶频率/Hz箱盖一阶频率/Hz 方案一有箱盖有泡棉37.1723.57 方案二无箱盖无泡棉35.75 方案三有箱盖无泡棉38.1323.57

根据三种状态电池包，设计相应振动工装，如图3－图5所示。整个试验布置5个加速度传感器，其中5号、6号为控制传感器，控制扫频试验过程中信号输入，布置在箱体吊耳处；4号、7号、8号为监测传感器，监测扫频过程中加速度响应及识别共振点，4号布置在底板处，7号布置在箱盖中间，8号布置在箱盖边缘。本文试验扫频速率10 ct/min，扫频段设置5～200 Hz，激励加速度0.5g，往返扫频2次，三种方案扫频测试数据汇总如表2所示。

图3 方案一实测现场与实测数据

图4 方案二实测现场与实测数据

图5 方案三实测现场与实测数据

表2 三种方案扫频测试数据汇总表 方案状态系统4号一阶频率/Hz系统7号一阶频率/Hz系统8号一阶频率/Hz箱盖一阶频率/Hz 方案一有箱盖有泡棉37.5338.1237.5327.06 方案二无箱盖无泡棉37.04 方案三有箱盖无泡棉37.6437.6439.3827.13

根据A项目试验和仿真结果，可以得出以下结论：

郁达夫与梁实秋论争时，一开始翻译了辛克莱Mammonart的第44章的最后五段和第45章的几乎全部，然后在1928年3月份到1929年8月份的时候持续翻译了Mammonart的19个章节。

1）箱盖内表面支撑泡棉对系统的刚度产生影响，即有泡棉支撑区域扫频结果38.12 Hz高于无泡棉支撑区域扫频结果37.53 Hz，这是因为支撑泡棉提高了系统箱盖的局部刚度；2）箱盖内表面无支撑泡棉时，箱盖中间区域的扫频结果37.64 Hz，低于箱盖边缘区域的扫频结果39.38 Hz，这是因为系统箱盖中间区域的刚度最弱，边缘区域刚度较高；3）三种试验状态，系统一阶频率即扫频结果最低的是状态二37.04 Hz；其次是状态一扫频结果为37.53 Hz；最高的是状态三，扫频结果为37.64 Hz，当系统单独增加箱盖后系统刚度有所提升，箱体的边框通过螺栓和箱盖连接到一起，导致系统刚度得到提高，仿真结果与扫频测试结果吻合度较高；4）状态一和状态三的箱盖扫频结果分别是27.06 Hz和27.13 Hz，和仿真结果23.57 Hz比较，在允许误差5%范围内。

3.2 B项目仿真试验对标

针对两种状态的系统分别进行了模态分析，根据输出结果文件中的质量参与系数，分别得到了有无支撑泡棉两种状态电池包及其箱盖的一阶固有频率，如图6所示。

(a) 无泡棉模态结果( f=37.3 Hz )

(b) 有泡棉模态结果( f=39.7 Hz )

图6 B项目电池系统模态分析结果

根据两种状态的仿真结果，对应设计了两种试验，分别对无泡棉和有泡棉开展扫频测试，测试过程如图7所示，扫频试验结果如图8所示。

和方差(SSE)为3.838，确定系数(R-square)为0.962 1，调整后确定系数(Adjusted R-square)为0.957 4，均方根(RMSE)为0.399 9。

(a) 无泡棉系统扫频测试样包

(b) 有泡棉系统扫频测试样包

图7 B项目电池系统扫频样包状态

图8 B项目有无泡棉电池系统扫频测试对比

根据B项目仿真与试验对标结果得出以下结论：

1）当箱盖刚度较大时，箱盖自身一阶频率23.4 Hz，粘贴泡棉后，系统刚度可以得到提升，电池包箱盖内表面没有粘贴泡棉时，系统的一阶频率为38.24 Hz，粘贴泡棉后，系统的一阶频率提升到39.86 Hz，系统一阶频率提高了1.62 Hz；2）本项目模态分析结果得到有无泡棉两种状态的系统一阶频率，对比扫频测试得到的结果，误差在允许范围5%以内，满足工程实践常用标准要求。

4 结论

本文模态分析结果与扫频测试结果吻合性较好，说明本文建模方法和系统各零部件材料参数设置是合理的；2）当电池包箱盖刚度较高或箱盖固频和系统固频越接近时，往往可以通过在箱盖内表面粘贴泡棉的方式提高系统刚度；3）箱盖扫频结果和系统扫频结果一致，因为箱盖本身并未被激励，由于激励信号由振动台传递至工装，然后传递至电池箱体，再至箱盖，过程中激励信号经过多次削弱，由于扫频加速度是一定的，低频时扫频能量较弱，最终导致箱盖未被激励；4）根据箱盖同一位置有无泡棉情况下扫频测试结果可知，在箱盖材料阻尼相同的情况下，箱盖下部有支撑泡棉情况增加了局部刚度，结构阻尼较小，因而产生一定的加速度响应，箱盖下部无支撑泡棉情况箱盖的刚度较弱导致结构阻尼较大，根据振动理论会出现响应低于激励的情况[10]。

参考文献

[1] 欧阳明高.汽车新型能源动力系统技术战略与研发进展[J].内燃机学报,2008,26(S1):107-114.

[2] 王品健.纯电动汽车动力电池包箱体结构轻量化设计与优化[D].长沙:湖南大学,2018.

[3] 陈雨,陈南,张宁,等.考虑精确电池单元体动力学建模的电动汽车动力电池包振动分析[J].噪声与振动控制,2018,38(S1):19-23.

[4] 冯富春,盛军,李彦良,等.通用电池系统及其转接支架刚强度及模态分析[J].时代汽车,2021(20):78-79.

[5] 兰凤崇,黄培鑫,陈吉清,等.车用电池包结构动力学建模及分析方法研究[J].机械工程学报,2018,54(8): 157-164.

[6] LI C,KIM I Y,JACK J.Conceptual and Detailed Design of an Automotive Engine Cradle by Using Topology, Shape,and Size Optimization[J].Structural and Multi- disciplinary Optimization, 2015,51(3):547-564.

[7] 杜嘉峰,贺廷俊,陈文斐,等.蓄电池支架螺栓预紧力试验对标及结构优化[J].汽车实用技术,2021,46(9): 97-99.

[8] WILLIAM T,MARIE D.Theory of Vibration with App- lications[M].Beijing:Tsinghua University Press,1998.

[9] 邱世涛,陈朝海,江吉兵.泡棉性能对电池模块膨胀力的影响[J].广东化工,2020,47(22):1-3.

[10] 庄表中,陈乃立.随机振动的理论及实例分析[M].北京:地震出版社,1985:216-222.

Research on Dynamic Modeling Methods and Influence Factors of Vehicle Battery Pack

LIANG Xinlong, FANG Youwei, ZHANG Long, LV Xixiang

( Hefei Gotion High-tech Power Energy Company Limited, Hefei 230011, China )

Abstract: The battery pack is difficult to analyze mechanical performance due to its complex mechanical, electrical, thermal and other components system, which brings great challenges to the subsequent benchmark. Therefore, it is particularly important to chose a reasonable modeling method.This paper uses the homogenized model equivalent method and fine pre-treatment, combined with the isotropic material performance data obtained by compression test method, to carry out modal simulation of the battery system and its zero parts respectively. Based on the sweep frequency test data, the validity and accuracy of the model are verified. The material data of the cell and the supporting foam is verified by the test and simulation benchmark. By comparing the sweep frequency test data with or without the foam and with or without the box cover, the influence law of the box cover and the supporting foam on the system stiffness is obtained, and the influence factors and reasons of the differences in the sweep frequency curves of several states are explained.

Keywords:Power battery pack;Modal analysis;Sweep frequency test;Damping coefficient

10.16638/j.cnki.1671-7988.2023.022.001

中图分类号：TM911；U469.7

文献标识码：A

文章编号：1671-7988(2023)22-01-06

作者简介：梁新龙（1988－），男，硕士，工程师，研究方向为动力电池包机械性能开发，E-mail:liangxinlong@gotion.com.cn。