疫情形势下的公交排队问题研究

2023-12-13范桂明陈琳

中国储运 2023年11期

文/范桂明陈琳

针对疫情形势下的公交车站排队问题，本文运用了排队论方法对这一排队现象进行分析与研究，并提出每辆公交车额外配备一名工作人员的建议，运用M/M/c模型进行具体案例分析，通过计算得出多服务台泊松到达、负指数服务时间模型，较单服务台泊松到达负指数服务时间模型在缓解排队拥堵问题上具有明显的优势，从经济角度分析M/M/2排队模型也更具有可行性。

引言

排队是我们生活中经常会遇到的一种现象，已有很多学者将排队论引入到实际应用当中[1-6]，本文主要针对疫情形势下的公交排队问题进行研究，乘坐交通工具无可避免需要排队，而疫情形势下乘客需要提供绿色健康码，甚至有的地区还需要准备好48小时内检测的核酸报告证明，对于现代社会的公交集团，每辆公交车只配一名司机（即一名工作人员），这就导致了公交车到站后司机需要检查每位乘客的健康码和核酸报告，难免一些老人不熟悉流程而耽误很多时间，于是乘客在一些站台前就排起了长队。本文将运用排队论方法对这一排队现象进行分析与研究，并提出每辆公交车配备两名工作人员的建议，运用M/M/c模型进行具体案例分析，结果表明此改进方法具有现实意义。

1.排队论理论

1.1排队论简介。排队论就是把排队时间控制在一定的限度之内，在服务质量的提高和成本的降低之间取得平衡的一种理论方法[7]。20世纪50年代初，D.G.Kendall对排队论作了系统研究，提出了用3个字母组成的符号表示排队系统，即A/B/C[8]。

1.2排队系统的组成。排队系统中的“顾客”指的是被服务的对象，“服务台”指的是提供服务的组织、机构或人，不同的服务系统正是由排队系统中的顾客和服务台组成。图1-1表示的是排队系统的结构，排队系统的组成包括输入过程、排队系统规则和服务机构（服务台）三要素。

1.2.1输入过程。输入过程就是顾客进入排队系统的过程，可以描述为在一定时间内到达了多少顾客，或者可以描述为先后两名顾客到达的时间间隔。

1.2.2排队规则。损失制：顾客看到服务台没有空闲随即离开的排队规则。等待制：顾客看到服务台没有空闲不会选择离开，而是继续等待，直到接受完服务的排队规则。

1.3排队系统的符号表示。一个排队系统模型的表示可以包含五个参数，形式为：A／B／C／D／E。A表示顾客到达的概率分布，一般取M（顾客到达服从泊松分布）。B表示排队系统中顾客到达服从的时间分布，它可以取负指数分布，用“M”表示；定长时间分布，用“D”来表示；任意服务时间分布，用“G”来表示等。C表示排队系统中有多少个服务台，一般取正整数。D表示排队系统能够容纳顾客的最大值，可取正整数或无穷大。E表示排队系统对顾客源是否有限制，可取正整数或无穷大。

1.4排队系统的数量指标[9]。在研究一个排队系统时需要一系列描述排队系统特征的数量指标，分析其运行效率，通常评价排队系统优劣有以下几项数量指标：λ：单位时间到达的顾客数；μ：单位时间服务的顾客数；P0：系统中无顾客的概率；Ls：系统中排队等待服务和正在服务的顾客总数；Lq：系统中排队等待服务的顾客数；Ws：顾客在排队系统中的逗留时间，即顾客在排队系统中的等待时间和接受服务的时间之和；Wq：顾客在系统中的排队等待时间；Pw：顾客得不到及时服务必须排队等待的概率；Pn：系统中恰好有n个顾客的概率。

2.排队模型

2.1M/M/1排队模型

M/M/1排队模型表示顾客到达服从参数为λ 的泊松分布，服务时间服从参数为μ 的负指数分布，则M/M/1排队模型相关数量指标计算公式为：

2.2M/M/c排队模型

在M/M/c排队模型表示顾客到达服从参数为λ 的泊松分布，服务时间服从参数为μ 的负指数分布，排队系统包括多个服务台，则M/M/c排队模型相关数量指标计算公式为:

1.系统中无顾客的概率

3.案例分析

3.1排队数量指标分析

本文选取天津某公交车站早班车为例，经过多次统计取近似平均值，乘客平均每分钟到达站台1.45人，公交车司机检查每名乘客健康码和核酸报告的平均时间为25秒，即乘客到达率λ=1.45人/分钟，司机的服务率μ=2.4人/分钟，建立数学模型并进行计算，结果如表3-1。

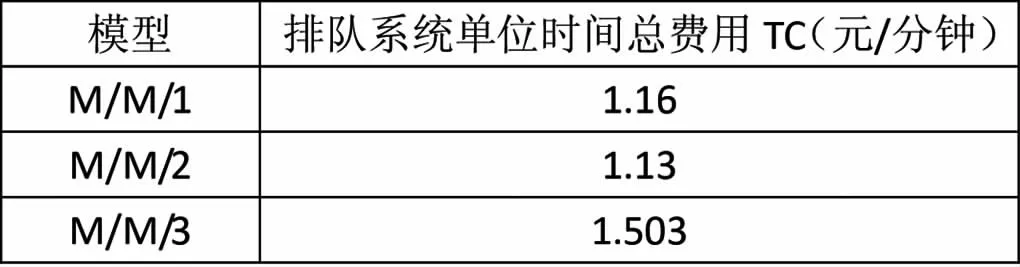
表3 -2 排队模型经济分析对比

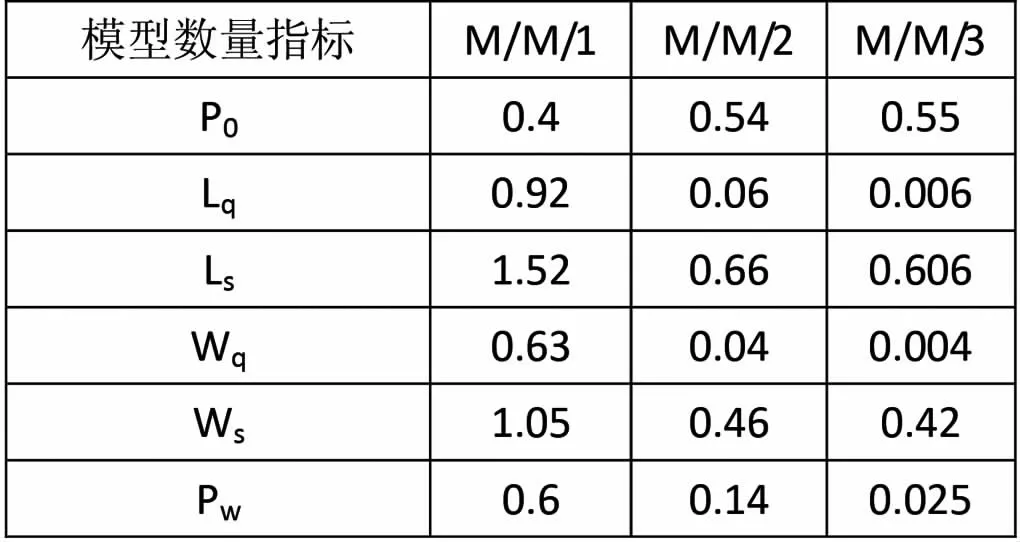
表3 -1不同模型数量指标的对比

从以上数据可以看出，只有一名工作人员（即只有司机）的排队系统并不能满足乘客的需求，上车乘客必须排队等待的概率为60%，系统里排队等待人数将近1人，每名乘客在排队系统里逗留时间超过1分钟，这就导致公交车在车站停留时间过长，严重影响乘客出行时间和公交系统的工作效率。为了改善这种长时间排队的状态，本文提出增加一名公交乘务工作人员，这样就形成了M/M/2的排队模型，从表中可以看出，上车乘客必须排队等待的概率降低为14%，系统中排队等待的乘客数减少为0.06人，每名乘客在排队系统里逗留时间也较M/M/1模型减少了一半，可见增加一名工作人员对于改善当前疫情形势下的公交排队问题具有积极意义。同理，表中M/M/3的数据表明继续增加一名工作人员工作效率会更高，但是还有一个重要因素，就是考虑公交集团的运营成本，即要对排队系统进行经济分析。

3.2排队系统经济分析

从上述排队系统相应数量指标分析可以看出，增加工作人员系统的效率的确提高了，但是我们还要分析运营成本，增加工作人员到底值不值得。从经济角度分析排队系统的优劣时，单位时间内，排队系统的总费用TC表示为服务机构或服务台单位时间的费用与单位时间内顾客逗留在排队系统的费用之和，即TC=cwLs+csc（16）

其中cw为每名顾客在排队系统里逗留单位时间产生的费用；Ls为上文系统中的顾客数；cs为每个服务台单位时间产生的费用；c为服务台的个数。本文中服务台单位时间产生的费用只考虑工作人员的工资，因为无论几个服务台，公交车其它运营费用都是不变的。经调研当地居民收入状况，cw估值为0.5元/分钟，cs为0.4元/分钟，计算各排队模型费用如表3-2。

从计算结果可以看出本文提出增加一名公交乘务工作人员的想法不仅能提高排队系统的工作效率，而且产生的费用也较M/M/1排队系统更低，而M/M/3排队模型虽然能够解决排队系统中拥堵的问题，但是消耗的费用也较高，综合比较M/M/2排队模型更加有优势。