基于响应面法的液压机械臂结构优化

2023-12-12孙凯

起重运输机械 2023年22期

孙凯

南京市特种设备安全监督检验研究院南京 210019

0 引言

在半个世纪前，计算机技术的发展给结构优化设计带来新的发展契机，涌现出大量的工程优化设计算法和软件[1]。高效的机械结构优化流程的实施离不开基础理论、力学分析手段和软件方法实现，这些基础学科的发展为工程设计者提供了清晰的设计思路和工具。目前，针对机械结构的优化设计主要分为尺寸优化、形貌优化、拓扑优化等，优化设计理论比较完备，且在各领域均有广泛应用案例，如Ansys、Nastran和Hyperworks等CAE分析软件中均已加入优化分析功能模块[2]。

近年来，国内外学者已将结构优化设计理论应用到机械臂设计中。Rout B K等[3]以平面机械手和四自由度机械臂为研究对象，以尺寸和质量为优化目标开展机械臂的优化设计，将对运行精度和重复定位精度的影响降到最小；Hedge G S等[4]采用拓扑优化技术对机械臂进行结构优化设计，以柔度、质量降低为优化设计的目标，将弹性位移、速度作为约束条件，实现了初步的优化目标；Zhou L L等[5]以机械臂的动力学性能为约束条件，利用有限元分析技术进行动应力计算，系统全面地考虑了传动链、零件尺寸等因素，对五自由度机械臂结构开展了以减重为目标的轻量化研究；罗忠等[6]针对细长机械臂结构优化问题，提出了一种基于刚度灵敏度分析的参数优化方法；管贻生等[7]将动力学分析与有限元分析相结合，基于动力学仿真寻找到最危险的机械臂姿态，对工业机械臂进行尺寸优化和拓扑优化，取得了良好优化效果；刘延杰等[8]以机械臂各臂的制造板材厚度为优化设计变量，提出了以柔性关节结构模态频率为目标的优化设计新方法，为了避免结构柔度过小，在优化过程中还增加了静态偏移量为约束条件；任亮等[9]利用灵敏度分析技术筛选优化设计参数，大大降低了待优化参数规模，并在此基础上对六自由度机械臂进行参数优化，同时达到了增大机械臂的模态频率、改善力学性能和轻量化等多个目标。

机械臂的结构优化设计以结构疲劳寿命、动柔度、经济性、可制造性等指标为约束条件，通过对机械臂的结构尺寸、形状、拓扑构型、材料、工艺等方面进行合理调整，使指定的性能指标达到最优（如质量最轻、能耗最小等）[10，11]。如图1所示，船用起重液压机械臂的主要功能是离岸吊装（如将船上的重物，通过起重机械臂运输到码头地面）一些重要精密设备对起吊过程中的冲击振动、平稳性要求尤为严格，需要对机械臂进行精密主动控制。机械臂自身的质量直接影响控制系统的响应速度，故起重机械臂的轻量化设计是重中之重。

图1 船用起重液压机械臂示意图

本文以图1中船用液压机械臂的实验室样机（相似缩比模型）为研究对象，进行刚柔耦合动力学建模，计算其在典型、完整工作循环中的各关节载荷时域响应。以机械臂结构轻量化设计为优化目标，以机械臂主承力构件—主臂板材厚度为待优化参数，以主臂最大米塞斯应力为约束边界，建立待优化参数与约束边界之间的多项式响应面模型；采用蒙特卡洛法在约束边界内进行全局寻优，得到机械臂轻量化设计结果；再将优化后的结构参数带入有限元模型中，验证优化结果的正确性。

1 基于多项式响应面法的优化设计理论

响应面法的基本核心是采用多项式或其他方法（如支持向量机函数、神经网络等）建立可以模拟实际系统输入输出关系的数学模型，避免求解规模巨大的有限元、多体模型，在提高分析效率的同时保证符合要求的精度。其中，多项式拟合法因其构造简单、物理意义明确，在工程实践中使用最广泛。多项式法线性拟合多元自变量与因变量的关系式为

式中：X1、X2、…、Xm为m个一般自变量，Y为因变量，β0、β1、…、βm为未知的回归系数，ε为随机误差。

为了计算回归系数，需要对X1、X2、…、Xm做n次测量，得到n组测量数据（Yi、Xi1、Xi2、…、Xim），i＝1、…、n，n＞m，则回归关系为

多项式响应面中的二阶多项式方法在工程应用中较普遍，其形式可表示为

式中：y（x）为系统的响应，可以为加速度信号值、应变值、模态特征值等；x＝（x1，x2，…，xm）为响应面中的样本点，即试验设计点；m为试验参数数量；β为回归系数。

结构优化设计的目的是在满足结构功能要求的前提下获得最优的解决方案，如尺寸最小、质量最轻，其流程主要包括定义目标响应和待优化参数、定义边界约束、优化计算等。

2 机械臂刚柔耦合动力学建模及分析

在机械臂结构优化设计中，需将结构最危险工况下的载荷作为边界条件输入到力学模型中。传统的筛选典型静力学工况的分析方法由于忽略了系统加减速过程、振动冲击等因素，且人工考虑极限工况可能会有遗漏，不能反映机械臂真实工作受力情况。为了计算液压机械臂在工作过程中各关节点的真实动态载荷用于后续结构优化的载荷输入条件，需进行刚柔耦合动力学分析。

在多体动力学软件MSC.ADAMS中，建立机械臂的刚体模型，并进行运动学仿真，评估模型的机构运动特性是否符合设计要求。再将有限元软件生成的包含机械臂主臂、伸缩臂网格信息、模态结果信息等的.mnf文件导入MSC.ADAMS软件中，并建立机械臂刚柔耦合动力学模型。刚柔耦合模型既可模拟机构运动学，又可同时研究柔性体的弹性位移、应变等力学响应。

模拟机械臂在真实工作状态将货物从船上运输到地面等各起吊工况下的动力学特性，同时进行主臂关节节点力计算。主臂关节动态载荷即为主臂结构优化载荷输入条件。机械臂刚柔耦合动力学模型及将货物从船上运输到地面时各关节节点的载荷如图2所示。

图2 机械臂刚柔耦合模型及关节载荷

在图2b中，液压机械臂的刚柔耦合模型将一个圆柱体重物负载从船舶平台运输到另外码头岸上，此为一个作业循环。机械臂的主臂和伸缩臂各具有前后2个关节，每个关节的受力沿X、Y、Z方向进行分解，共计12个分量，如图2a所示。在刚柔耦合动力学模型中，液压机械臂将货物从船上运输到地面的过程中4个典型时刻（即起吊开始、提升阶段、平移运送负载、释放负载等时刻）的机械臂米塞斯应力云图如图3所示。

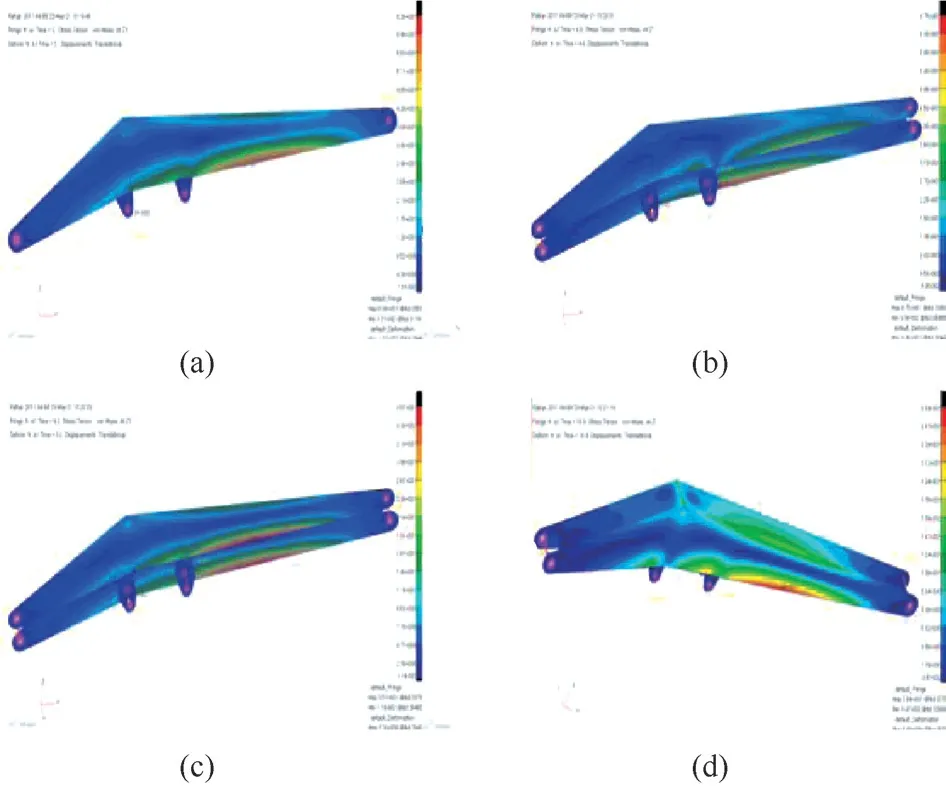
图3 4个时刻主臂米塞斯应力云图

由图3可知，主臂米塞斯应力较大的部位在其内侧受压处，且受力较均匀，应力集中情况较少。保证应力云图中每一点都符合安全系数要求是轻量化过程中的约束条件，主臂总质量只需用其板材厚度和密度经过简单代数运算即可求出，而主臂板材厚度与主臂最大米塞斯应力之间无显式的数学关系表达式，需要采用响应面模型进行描述。

3 基于响应面法的机械臂结构优化

3.1 试验设计

试验设计是关于怎样合理安排试验的数学方法，其确定了设计点的数量及分布规律，是建立高精度响应面的首要步骤。常用的试验设计方法包括全因子、均匀试验设计、正交试验设计等。拉丁超立方抽样（Latin Hypercube Sampling，LHS）是一种分层的随机抽样方法，可改进抽样策略，使产生的随机数更具代表性。LHS抽样能以较少采样次数获得较高的采样精度，其采样点均匀分布于设计区间内，而非集中在中值区域。如图4所示，将主臂按加工过程中的板材结构分布进行材料划分。

图4 参数分区示意图

在图4中，1、2、3为在机械臂制造过程中的钢板分区，每个分区由一整块金属板材焊接而成，每个分区采用同一厚度规格的板材，选取板材厚度为待优化参数。采用LHS方法对主臂区域Ⅰ、区域Ⅱ、区域Ⅲ（对应的板材厚度参数为P1、P2、P3）进行抽样，综合考虑建模速度和精度，抽样点数为100个，参数P1、P2、P3的初始值为10 mm。根据工程经验，抽样上下边界均为参数初始值的50%～150%。

3.2 多项式响应面建立

建立响应面模型可以模拟原始有限元模型的输入输出关系。在结构优化迭代过程中，只需在响应面模型中进行拟合计算，即可避免反复调用耗时较长的有限元求解器。此外，该方法同时具有数据精度高、计算速度快等优点。将100个试验设计点分别输入有限元模型中，计算出100个对应的主臂最大米塞斯应力。通过尝试，选用5阶多项式方法拟合样本点，建立3个设计参数（P1、P2、P3）和主臂最大米塞斯应力之间的响应面模型，其中区域Ⅰ、区域Ⅱ的板材厚度与最大应力之间的响应面模型如图5所示。

图5 区域Ⅰ、区域Ⅱ响应面模型

在图5中，横纵坐标表示当区域Ⅰ、区域Ⅱ板材厚度从0.5 mm变化到1.0 mm时，竖坐标表示主臂最大米塞斯应力从62.0 MPa变化到145.0 MPa。

在实际工程问题中，响应面模型的精度和泛化能力必须满足一定的要求，故所建立的响应面模型都要按照一定的指标进行精度评价。本文通过常用的均方根误差(RMSE)及决定系数R2这2种标准对响应面模型精度进行评估。其表达式为

式中：y、ys为设计空间中各样本点对应的试验真值和代理模型预测值；为设计空间上各点的均值；RMSE为设计空间各点试验真值和代理模型预测值之间误差占平均幅值的百分比；R2为决定系数，即试验真值与代理模型预测值之间的总体差异程度，取0～1。

如果R2越接近1、RMSE越接近0，则代理模型越能反映真实的参数和响应之间的关系。通过对响应面进行检验，决定系数R2均大于0.99，相对均方根误差RMSE均小于0.001，响应面模型精度满足工程要求。

3.3 基于蒙特卡洛法的响应面寻优

采用蒙特卡洛法求解响应面最优问题既可避免求解过程陷入局部最优，也可兼顾较高的求解效率。在设计参数的取值空间内，再次采用拉丁超立方抽取2万个样本点。由于LHS为分层均匀抽样，2万个样本点从概率学上能完全覆盖3个参数的取值空间。

将2万个样本点带入响应面模型中，计算主臂在严苛工况工作下的最大米塞斯应力。结果显示，米塞斯应力为62.0～145.0 MPa。机械臂采用LY12材料制造，其屈服强度为325.0 MPa。在实际工程中，结构取4倍安全系数，即材料许用应力为81.25 MPa。在图6中，区域Ⅰ、区域Ⅱ、区域Ⅲ板材厚度为一个参数取值的组合，如区域Ⅰ、区域Ⅱ、区域Ⅲ的板材厚度取6.5 mm、8.2 mm、9.8 mm时为一个满足许用应力要求的参数组合，即一个样本点。图6为从2万个样本点中筛选出的3 799个满足材料许用应力要求的样本点。计算3 799个样本点对应的主臂质量，最小质量为74.5 kg，区域Ⅰ、区域Ⅱ、区域Ⅲ的最薄板材厚度组合为8.49 mm、5.60 mm、5.27 mm。

图6 满足条件的样本点

4 优化结果二次验证

考虑到板材厚度为标准化、系列化，取3个板材厚度分别为8.5 mm、5.6 mm、5.3 mm。相比优化前的10 mm初始厚度，主臂板材厚度下降了15%～47%，总质量降低了26%。将上述优化设计结果带入原始有限元模型中，进行结果二次验证确认。在机械臂主臂上，选取应力最大的区域内6个典型位置，计算每个位置危险有限元网格单元的米塞斯应力。图7为一个工作循环中机械臂应力最大的6个区域的米塞斯应力曲线。