南海东部海相砂岩油藏水平井与定向井折算比例研究

汤小龙，徐伟，缪云，张晓林，孙维

(中海石油(中国)有限公司深圳分公司，广东 深圳 518067)

0 引言

井网适应性评价是评价油藏开发井网是否合理的重要手段，业界经常用如式(1)所示的谢尔卡乔夫公式来进行井网适应性评价[1-4]。在谢尔卡乔夫公式中井网密度S是一个重要参数，在原始公式中指的是定向井井网密度，但南海东部油田经常采用定向井与水平井的混合井网开发油藏，这种情况下如何有效地计算井网密度，目前相关的研究较少。前人一般根据经验，将1 口水平井等效为2～5 口定向井，进行井网密度的近似换算[5-8]。但实践表明，由于不同油田地质油藏特征的差异，不同油藏的水平井与定向井的等效比例应当是不同的，目前关于这方面的研究较少。

式中：ER为油藏最终采收率(%)；ED为油藏驱油效率(%)；a为井网指数；S为井网密度(口/km2)。

本文引入水平井与定向井折算比n的概念，定义n为相同生产状态下水平井波及范围与定向井波及范围比值，同时采用解析法、矿物资料折算法及数值模拟法等三种方法计算折算比n，通过三种方法的对比得到不同类型油藏的折算比以及相应的影响因素。这一研究成果的可方便一线科研人员开展井网适应性评价，提高评价效率。

1 解析法计算

对边水油藏，假设中心部署一口定向井开发，流动形态是径向流(图1)，流动供给半径为R；若部署一口水平井开发，水平井为椭圆流模式(图1)，长轴为a，短轴为b，水平井长度为L，可以分别计算两种井的泄油范围Sv和Sh，如式(2) 和式(3) 所示。折算比相当于水平井波及范围与定向井波及范围，如式(4)所示：

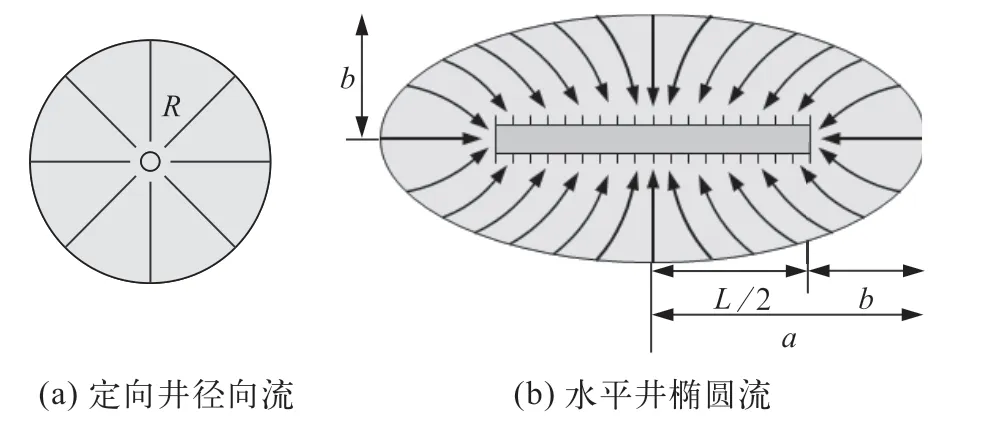
图1 边水油藏定向井径向流和水平井椭圆流示意图

在边水油藏中，当水平井长度延长，折算比增加，水平井长度变小，折算比降低；在水平井长度相同时，随动用半径的增加，折算比降低，如图2 所示。当然稀油和稠油由于动用范围差异，折算比也会不同。例如稠油油藏动用半径600 m，稀油动用半径800 m，水平井长度按照500 m 计算，得到稀油边水油藏折算比为1.31，而稠油的折算比为1.42，存在差异。但从总体情况看，折算比在1.00～2.50 之间变化，即边水油藏采用水平井开采与定向井开采相比，优势不算非常明显。

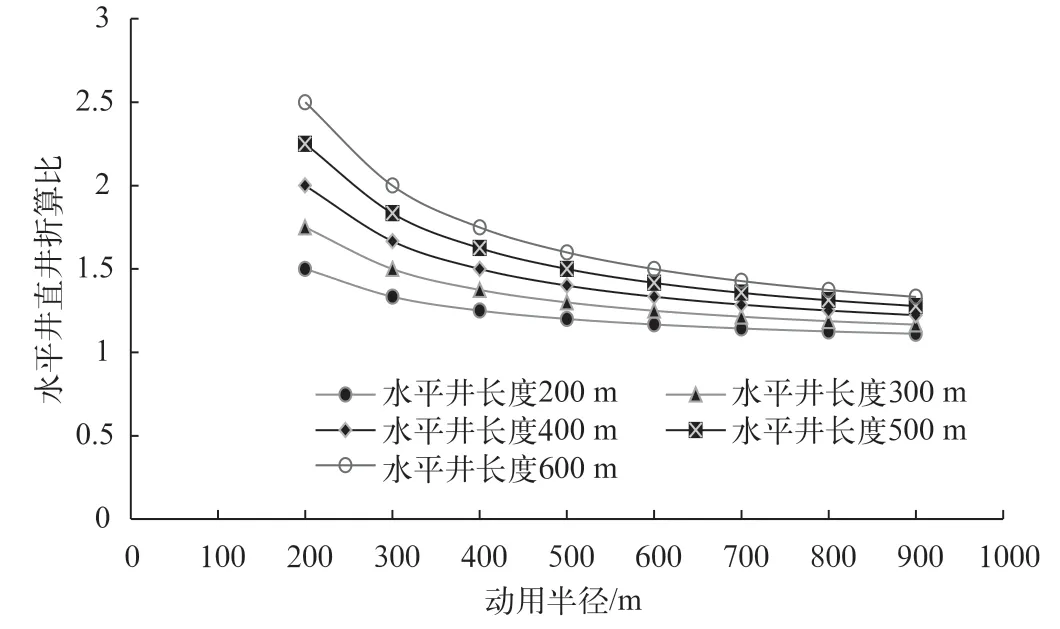
图2 边水油藏水平井长度和动用范围对折算比影响

对底水油藏，采用定向井开采时产生底水锥进，形成的波及范围是锥体(图3)，其锥体底部圆形半径为r；对水平井形成的是水脊，可以视为两个半锥体和一段水脊体组成(图3)，底部锥体半径为R，其中r≠R；这两种情况下的波及范围计算如式(5)和式(6)所示，折算比n可以用式(7)计算：

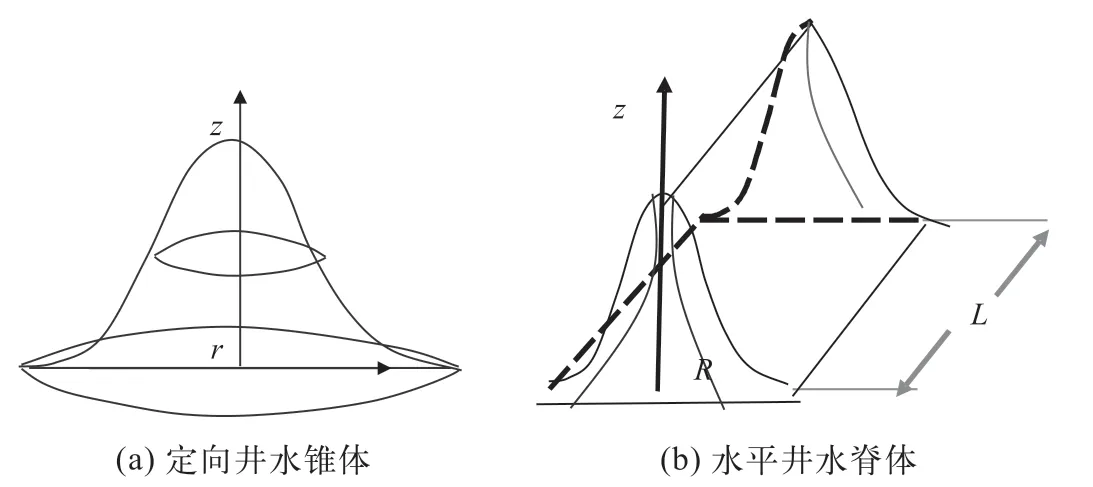
图3 底水油藏定向井水锥体和水平井水脊体示意图

由于流动模式和来水方向存在差异，锥体半径取值有差异。经过RPM 测试及动态分析表明，对水平井来说，稀油边水油藏的波及范围约800 m，底水油藏波及范围600 m，而稠油的底水油藏波及半径在150～600 m。

底水油藏来说，动用范围和水平井长度是影响折算比的重要参数。随着水平井长度增加，折算比增加；动用范围越小，折算比越大，反之动用范围越大，折算比越小，如图4 所示。例如当底水油藏无夹层时，水平井动用半径取值150 m，定向井动用半径取值60 m，计算得到折算比为26.15；而底水油藏有夹层时水平井动用半径取值600 m，定向井动用半径300 m，计算折算比为7.18。

图4 底水油藏水平井长度和动用范围对折算比影响

2 矿场资料折算法

根据折算比的定义，在相同地质和油藏条件下，水驱油效率是相同的，因此波及范围比值与累积产油量比值是相同的，所以折算比也可以采用两种井型的累积产油量对比。在类似油藏条件下分别统计定向井和水平井在相同含水率下的累产油量，计算折算比。如表1 所示，对于边水油藏来说，不同油藏的水平井定向井折算比在1.49～17.48，平均为8.24。如表2 所示，底水油藏有3 口定向井生产历史比较完整，满足与水平井具有相同的含水阶段的条件(含水条件95%)，定向井平均累产油5.04×104m3，水平井单井平均累油是20.42×104m3，折算比为4.05。

表1 某典型海相砂岩油田边水油藏折算比统计

表2 某典型海相砂岩油田底水油藏折算比统计(含水95%)

矿场资料统计法采用的是类似油田定向井和水平井累产油数据，由于地质油藏条件是变化的，而且符合具有相同含水阶段、油藏原油黏度类似的对比条件的样本较少，因此该种方法得到结果不一定有代表性，建议仅供参考。

3 数值模拟计算法

分别建立单井底水油藏和边水油藏的定向井模型、水平井模型，如图5 所示，利用数值模拟方法计算，确定两种井型的折算比。概念模型中根据实际地质油藏特征，考虑了不同流度，分别建立了3.0×10-3、3.8×10-3、5.0×10-3、7.5×10-3、15.0×10-3、30.0×10-3、50.0×10-3、150.0×10-3、500×10-3μm2/ (mPa·s) 等9 种流度模型开展计算。对计算出的结果，分别统计不同含水时刻的定向井和水平井波及范围比值，绘制图版，表征折算比变化。

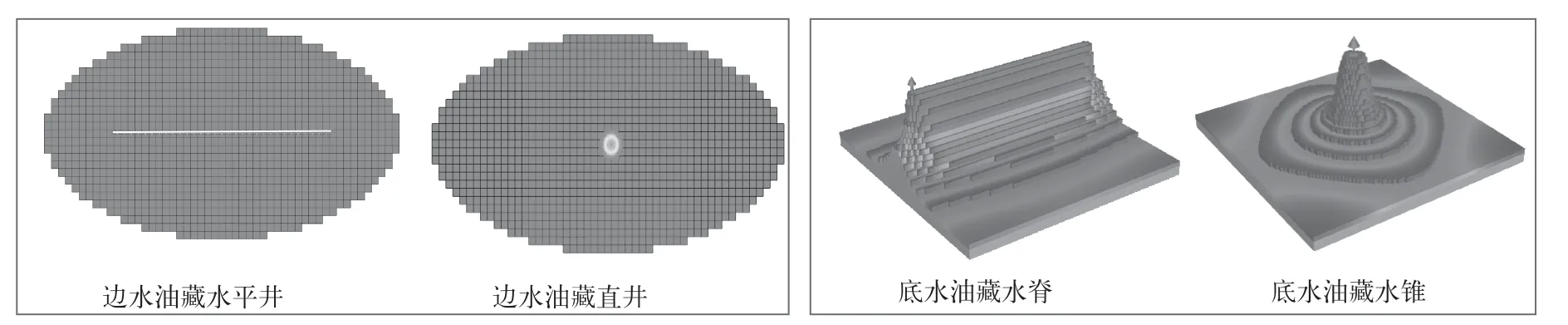
图5 边水油藏概念模型和底水油藏概念模型

从图6 可以看出，边水油藏的折算比最大不超过4；流度越大折算比越小，流度越小，折算比越大，水平井优势越明显；随含水增加，折算比逐渐减小，尤其到高含水期，折算比快速降低，当含水率大于95%以后，折算比都不超过2。

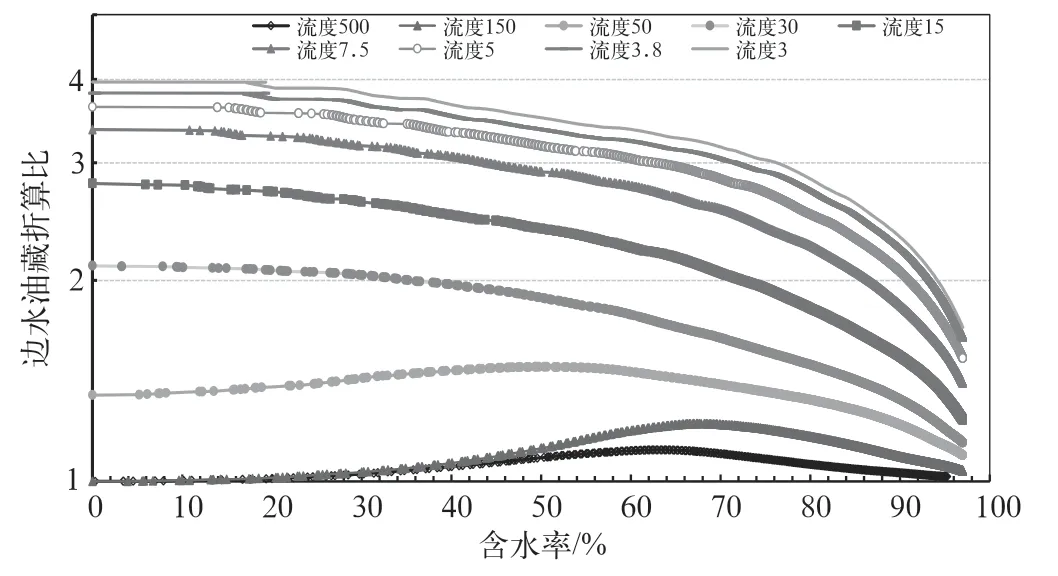
图6 边水油藏不同流度下水平井定向井折算比

图7 显示了底水油藏折算比，很明显底水油藏的折算比较边水油藏高的多。流度为3 时初期折算比达到89 倍。随着流度增加，折算比降低，例如流度15 时，含水50% 时的折算比为21.5，而流度150 时含水率50%的折算比为9.2。随含水率增加，大部分折算比是降低的，越到高含水阶段折算比越小。在高流度情况下(流度＞30)，有一定的反常情况，即在90%之前，随含水率增加，折算比增加，而在90% 以后折算比才会降低，造成这种现象的原因是：定向井水锥突破快，在见水后水锥体增加速度减小，而水平井含水上升慢，水脊体增加速度快，因此造成折算比增加；当水平井见水后，含水快速上升，水锥体增加速度减慢，折算比开始降低。以目前含水条件作为折算比的对比界限，可以得到不同流度下的折算比数值。

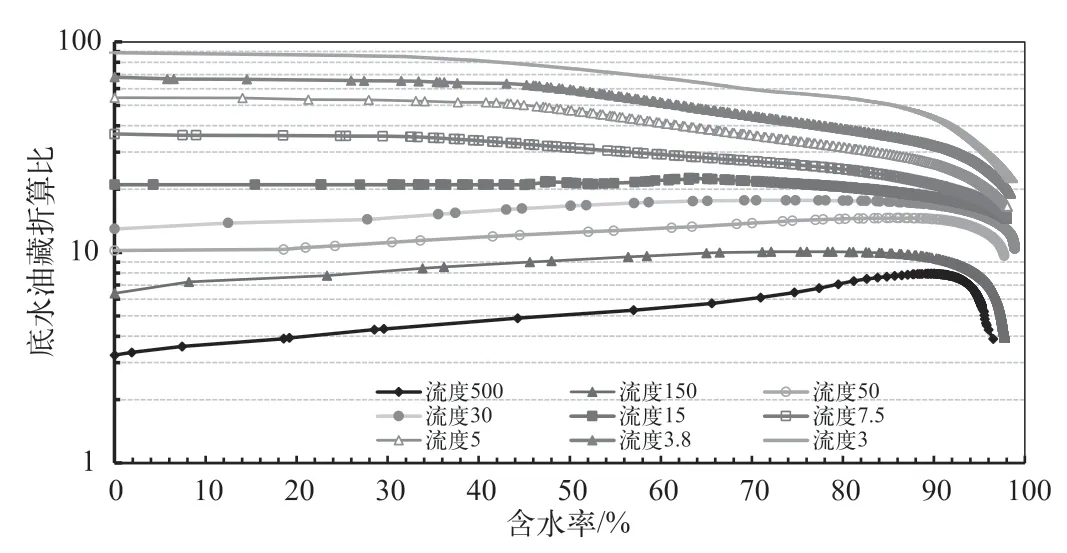
图7 底水油藏不同流度比下的水平井定向井折算比

4 三种方法对比

综合考虑三种方法的计算结果(表3)，其中数值模拟方法与理论解析方法计算结果比较一致。为了统一选择标准，确定以理论解析计算结果为最终选择，即：稀油边水油藏水平井与定向井折算比采用1.31，稠油边水油藏水平井与定向井折算比采用1.42；稀油底水油藏水平井与定向井折算比采用7.18，稠油底水油藏水平井与定向井折算比采用26.15。

表3 折算比计算结果统计表

通过明确四类油藏的水平井与定向井折算比例，再结合式(1)，即可有效实现井网适应性评价，判断井网合理性。

5 结论

(1)通过解析法、矿场资料折算法和数值模拟法三种方法，首次明确了稀油边水、稠油边水、稀油底水和稠油底水4 类油藏的水平井与定向井折算比例，极大提高开发井网适应性评价的效率和准确度。

(2)水平井与定向井折算比与水平井长度及动用范围有关，随着水平段减小、动用范围增加，水平井与定向井折算比降低。