“双碳”目标下绿色金融助力经济低碳转型的机制研究——基于绿色索罗模型

孟 禹 郭 凯，2 张莹莹

（1.东北财经大学，大连 116025；2.辽宁（大连）自贸区研究院，辽宁 116025）

内容提要：本文基于2006 年-2020 年30 个省份面板数据，采用系统GMM 模型实证分析和验证了绿色金融助力经济低碳转型的作用机制，进一步探究了不同碳排放水平下，绿色金融助力经济低碳转型的作用机制是否存在异质性。研究发现，绿色金融可以助力经济低碳转型；在当前的能源结构和绿色全要素生产率水平下，绿色金融可以同时通过能源结构和绿色全要素生产率的调节机制助力经济低碳转型。但能源结构和绿色全要素生产率的调节机制存在区域异质性，在高碳排放地区能源结构的调节机制没有发挥出来，绿色全要素生产率的调节机制为负向，在低碳排放地区能源结构和绿色全要素生产率均发挥了正向的调节机制。

一、引言

2020 年，我国提出“双碳”目标，表明了大力推动绿色低碳发展的决心。绿色金融依据国家环保政策可以为清洁能源、绿色环保等改善环境、应对气候变化的项目在投融资、运行、风险管理方面提供有针对性的金融服务，可以引导经济向低碳发展方向转型和升级，是实现经济低碳转型不可或缺的重要力量。国内外学者研究均证实了绿色金融是实现经济可持续发展、协调人与自然的重要保障（王瑶和曹畅，2015；Soundarrajan 和Vivek，2016；朱四荣，2019）。绿色金融具有节能减排效应，但绿色金融是否助力了经济低碳转型？绿色金融发挥经济低碳转型作用的具体机制是什么？都是急需探究的重要议题。为此，本文从理论和实证两个方面系统剖析了绿色金融助力经济低碳转型的作用机制。本文的创新之处：（1）研究视角的创新。为实现“双碳”目标需要推动经济低碳转型，本文以现实问题为导向，将研究视角放在绿色金融助力经济低碳转型上，在丰富相关文献的基础上，可以为实现2030 年“碳达峰”，2060 年“碳中和”提供研究启示。（2）研究方法的创新。本文在Brock 和Taylor（2010）构建的绿色索罗模型基础上，创新性地引入绿色金融因素进行模型拓展，为分析绿色金融助力经济低碳转型提供一个改进的理论分析框架。

二、理论分析与研究假设

本文在Brock 和Taylor（2010）构建的绿色索罗模型的基础上，引入绿色金融变量进行理论拓展。模型的主要假设：污染排放是生产过程中的副产品（亦即将污染作为一种非期望产出），模型的主要设定如下：

式中，Y 为总产出水平；K、B 和L 分别为考虑了环境治理的“绿色”资本存量、劳动的有效性和劳动力数量；G 为绿色金融治理环境污染的投入量，vG为绿色金融治理环境污染的投入量在总资本中的占比；R 为不可再生能源，vR为不可再生能源的消耗量在总资本中的占比；I 为总投资；s 和δ 分别为储蓄率和折旧率；、和分别为“绿色”资本存量、劳动有效性和劳动力数量随时间的变化率；gB为劳动有效性（亦即用于生产的技术水平）的增长率；n 为外生的人口增长率；E 为污染排放总量；Ω 表示环保技术水平（绿色全要素生产率），大小为gA；a 为一个强度减排函数，a'＜0 而a''＞0。

假设生产函数是柯布-道格拉斯且规模报酬不变。将模型的主要变量（Y、K、E）进一步整理为单位有效劳动的形式（用小写字母表示）：

将主要变量转换为单位有效劳动的水平，进一步计算其增长率：

e 与碳排放总量E 之间的关系如下：

根据公式（2）-（16）得到碳排放总量的增长率：

当最终经济达到稳态时，单位有效劳动资本存量k 的增速将为0，污染排放总量以恒定速度gE=n+gB+gR-(gA+gG)下降，在T 时点达到峰值后再逐渐下降的过程，如图1 所展示。从图1 可以看出，当不考虑绿色金融时，单位有效劳动资本存量的增长率gk=ska-1-(n+δ+vR+gB)对应于图1 中的曲线Ⅰ，如果碳排放总量的增长率等于零时对应的gk可以表示为：对应于图1 中的直线Ⅲ，与曲线Ⅰ相交于点A；当考虑绿色金融因时，单位有效劳动“绿色”资本存量的增长率gk=ska-1-(n+δ+vG+vR+gB)对应于图1 中的曲线Ⅱ，如果碳排放总量的增长率等于零（g'EE=0） 时对应的 gk可以表示为：对应于图1 中的直线Ⅳ，与曲线Ⅱ相交于点B。因此，绿色金融使曲线由Ⅰ移动到曲线Ⅱ，曲线由Ⅲ移动到曲线Ⅳ，对应的碳排放强度曲线由Ⅴ移动到Ⅵ。基于上述分析，本文提出以下假设：

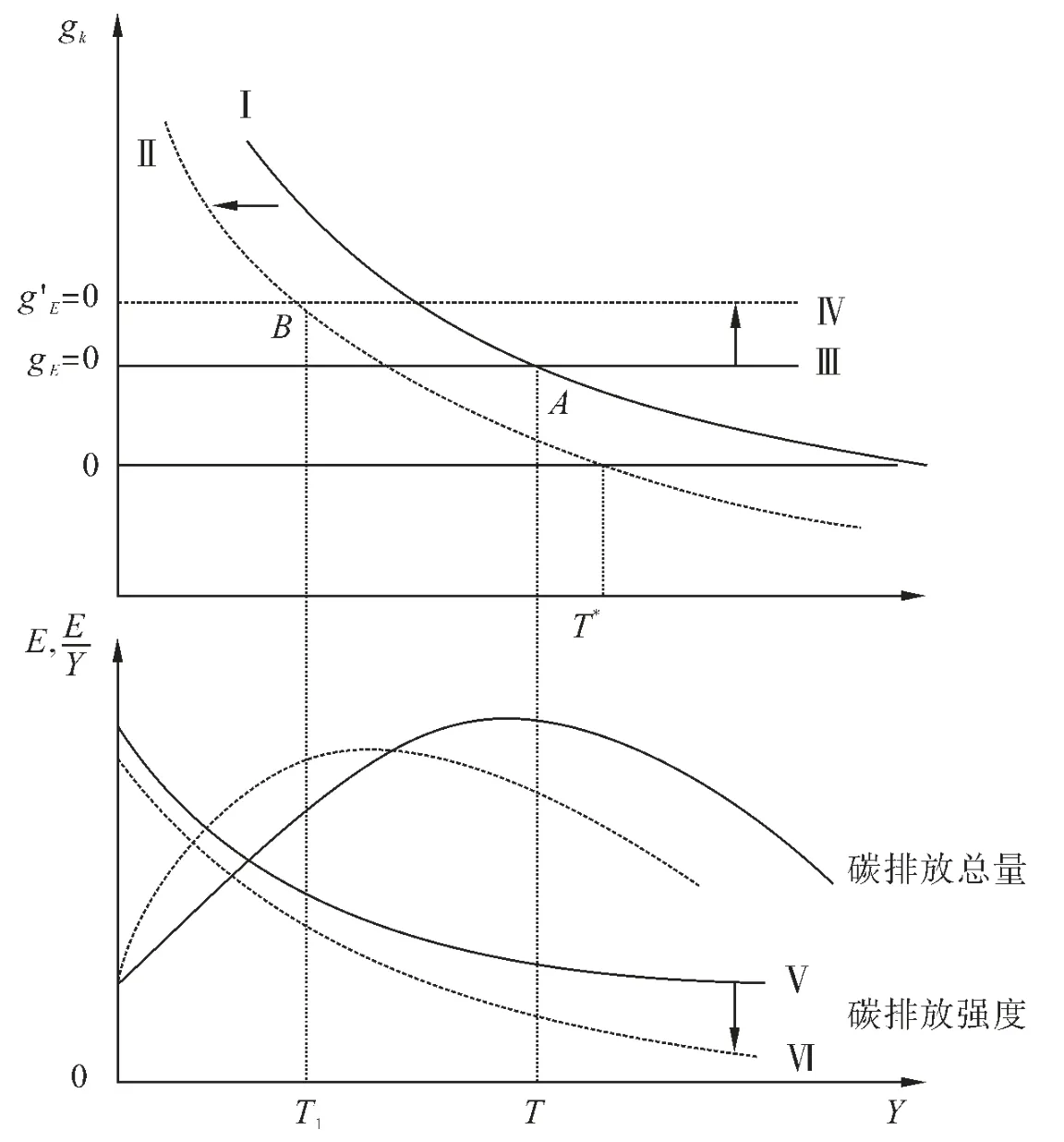
图1 基于绿色索罗模型的环境库兹涅兹曲线

H1：“双碳”目标下，绿色金融可以助力经济低碳转型。

（一）基于能源结构的调节机制

绿色金融对碳排放强度的影响如图2 所示。从图2 可以看出，在包含绿色金融与碳排放强度的绿色索罗模型中，当不减少不可再生能源的消费（gR）时，单位有效劳动“绿色”资本存量的增长率gk=ska-1-(n+δ+vG+vR+gB)对应于图2 中的曲线Ⅰ，如果碳排放总量的增长率等于零时对应的gk可以表示为：对应于图2 中的直线Ⅲ，与曲线Ⅰ相交于点A；当减少不可再生能源的消费（gR）时，单位有效劳动“绿色”资本存量的增长率g'k=ska-1-(n+δ+vG+vR′+gB)对应于图2 中的曲线Ⅱ，如果碳排放总量的增长率等于零时对应的gk可以表示为：，对应于图2 中的直线Ⅳ，与曲线Ⅱ相交于点B。又因为根据公式（17）碳排放总量的增长率gE=agk+n+gB+gR-(gA+gG)，那么减少不可再生能源的消费（gR）意味着相同的经济产出伴随着更少的碳排放。因此，在能源结构的调节下，绿色金融通过调整使曲线由Ⅰ移动到曲线Ⅱ，曲线由Ⅲ移动到曲线Ⅳ，对应的碳排放强度曲线由Ⅴ移动到Ⅵ。基于上述分析，本文提出以下假设：

图2 能源结构调节下的环境库兹涅兹曲线

H2：“双碳”目标下，绿色金融通过能源结构（降低不可再生能源的消费）的调节机制可以助力经济低碳转型。

（二）基于绿色全要素生产率的调节机制

绿色金融对碳排放强度的影响如图3 所示。从图3 可以看出，在包含绿色金融与碳排放强度的绿色索罗模型中，当还未提高绿色全要生产率（gA）时，碳排放总量的增长率等于零时对应的gk可以表示为：对应于图3 中的直线Ⅰ，与gk曲线相交于点A；当提高了绿色全要生产率（gA）时，碳排放总量的增长率等于零（g'E=0）时对应的gk可以表示为：对应于图3 中的直线Ⅱ，与gk曲线相交于点B。又因为无论是否提高绿色全要生产率（gA），对单位有效劳动“绿色”资本存量的增长率gk=ska-1-(n+δ+vG+vR+gB)没有影响。因此，在绿色全要素生产率的调节下，绿色金融通过调整使曲线由Ⅰ移动到曲线Ⅱ，对应的碳排放强度曲线由Ⅴ移动到Ⅵ。基于上述分析，本文提出以下假设：

图3 绿色全要素生产率调节下的环境库兹涅兹曲线

H3：“双碳”目标下，绿色金融通过绿色全要素生产率的调节机制可以助力经济低碳转型。

三、研究设计

（一）实证模型

本文研究绿色金融助力经济低碳转型的作用机制，由于经济增长存在惯性，上期经济增长会对当期的经济增长产生影响，同理上期的碳排放会对当期的碳排放产生影响，显然会存在滞后的被解释变量与误差项相关，直接进行OLS 估计是有偏且不一致的。广义矩估计（GMM）可以允许误差项存在异方差和序列相关，能通过将变量的滞后项作为工具变量解决模型中的内生性问题，显然GMM 模型更适用于本文的研究。因此，本文采用GMM 模型，模型构建如下：

其中，下标i 为省份标识，t 为年份标识，i=1，2，…30；t=1，2…；α1…α5为常数项，β11…β55均为待估系数；CGit表示GDP 碳排放强度，GFit表示绿色金融，ESit表示能源结构；GTFPit表示绿色全要素生产率；Zit表示控制变量的集合；ηi代表个体效应，μt代表时间效应，εit为残差项。

（二）变量选择与数据来源

1.被解释变量

GDP 碳排放强度。本文选择GDP 碳排放强度（CG=CO2/GDP）来衡量经济低碳转型。

2.解释变量

（1）绿色金融。本文借鉴高锦杰（2021）的做法，选取了绿色信贷、绿色投资、绿色保险、政府支持四个维度，如表1 所示。数据来源于各省份《统计年鉴》以及《中国保险年鉴》。

表1 绿色金融指标构建

（2）能源结构。本文采用清洁能源与高耗能能源消费量的比值来衡量能源结构，记为ES。数据来源于《中国能源统计年鉴》。

（3）绿色全要素生产率。本文借鉴Tone（2001）和Oh（2010）采用SBM-GML 方法测算我国30 个省（市）的绿色全要素生产率，记为GTFP。本文选取的投入指标如表2 所示，样本数据均来源于《中经网统计数据库》。

表2 采用SBM-GML 方法测算各省GTFP 的投入与产出指标

3.控制变量。借鉴现有文献，本文控制变量的选择如表3 所示。样本数据均来源于《中经网统计数据库》。

表3 变量定义及测度

（三）变量的描述性统计

本文的数据结构为2006 年-2020 年的省域数据，表4 是本文样本数据的描述性统计。从表中可以看出GDP 碳排放强度（CG）、能源禀赋（ESR）、对外开放程度（Open）和物价水平（CPI）的最小值与最大值差异较大。

表4 样本数据的描述性统计

四、实证结果分析

（一）面板单位根检验

表5 是各变量的单位根检验结果。从表中看出，各变量均在1%的统计水平上显著，因此，本文的样本数据均满足平稳性条件。

表5 ADF 单位根检验结果

（二）实证结果分析

表6 中的第（1）列是绿色金融对GDP 碳排放强度的估计结果。从表中可以看出，绿色金融对GDP碳排放强度的回归系数为-3.0351，在1%的统计水平上显著，说明绿色金融可以显著降低GDP 碳排放强度。由此，假说H1 得到验证。

表6 全样本系统GMM 的实证估计结果

从表6 中第（2）列可以看出，绿色金融对GDP碳排放强度的回归系数为-2.1817，在10%的统计水平上显著；能源结构对GDP 碳排放强度的回归系数为-4.0903，在1%的统计水平上显著。从表6 中第（3）列可以看出，绿色金融与能源结构的乘积项对GDP 碳排放强度的回归系数为-10.2869，在1%的统计水平上显著，说明能源结构的调节效应存在。同时，绿色金融对GDP 碳排放强度的回归系数为-4.2525，在1%的统计水平上显著；能源结构对GDP 碳排放强度的回归系数为-7.6039，在1%的统计水平上显著。说明通过能源结构的调节效应增强了绿色金融对GDP 碳排放强度的抑制作用。由此，假说H2 得到验证。

从表6 中第（4）列可以看出，绿色金融对GDP碳排放强度的回归系数为-1.5192，在1%的统计水平上显著；绿色全要素生产率对GDP 碳排放强度的回归系数为-1.1370，在1%的统计水平上显著。从表中第（5）列可以看出，绿色金融与绿色全要素生产率的乘积项对GDP 碳排放强度的回归系数为-3.4325，在5%的统计水平上显著，说明绿色全要素生产率的调节效应存在。同时，绿色金融对GDP碳排放强度的回归系数为-6.2850，在5%的统计水平上显著；绿色全要素生产率对GDP 碳排放强度的回归系数为-1.1370，在1%的统计水平上显著。说明通过绿色全要素生产率的调节效应增强了绿色金融对GDP 碳排放强度的抑制作用。由此，假说H3得到验证。

五、进一步分析

本文按照碳排放量的差别划分出高碳排放地区和低碳排放地区①按照碳排放水平的不同进行划分，碳排放前15 个省份为高碳排放地区，包括山东、河北、山西、江苏、内蒙古、辽宁、河南、广东、浙江、陕西、新疆、安徽、湖北、黑龙江、湖南；碳排放后15 个省份为高碳排放地区，包括四川、贵州、上海、吉林、福建、云南、广西、江西、甘肃、宁夏、天津、重庆、北京、海南、青海。进行异质性分析。

（一）高碳排放地区

表7 中的第（1）列是高碳排放地区绿色金融对GDP 碳排放强度的估计结果，从表中可以看出，绿色金融对GDP 碳排放强度的回归系数为-9.3141，在10%的统计水平上显著，说明在高碳排放地区绿色金融可以显著的降低GDP 碳排放强度。由此，假说H1 在高碳排放地区得到验证。

表7 高碳排放地区系统GMM 的实证估计结果

从表7 中第（2）列可以看出，高碳排放地区绿色金融对GDP 碳排放强度的回归系数为-3.7310，在10%的统计水平上显著；能源结构对GDP 碳排放强度的回归系数为-5.3369，在1%的统计水平上显著。从表7 中第（3）列可以看出，在高碳排放地区绿色金融与能源结构的乘积项对GDP 碳排放强度的回归系数为-11.8122，但在统计水平上不显著，说明在高碳排放地区能源结构的调节效应不存在。由此，假说H2 在高碳排放地区未得到验证。

从表7 中第（4）列可以看出，高碳排放地区绿色金融对GDP 碳排放强度的回归系数为-9.3222，在10%的统计水平上显著；绿色全要素生产率对GDP碳排放强度的回归系数为-1.0219，在10%的统计水平上显著。从表中第（5）列可以看出，绿色金融与绿色全要素生产率的乘积项对GDP 碳排放强度的回归系数为15.3071，在5%的统计水平上显著，说明绿色全要素生产率的调节效应存在。同时，绿色金融对GDP 碳排放强度的回归系数为-9.6699，在1%的统计水平上显著；绿色全要素生产率对GDP 碳排放强度的回归系数为-4.3199，在1%的统计水平上显著。说明在高碳排放地区绿色全要素生产率的调节效应虽然存在，但绿色全要素生产率的正向调节机制没有发挥出来。由此，假说H3 在高碳排放地区未得到验证。

（二）低碳排放地区

表8 中的第（1）列是低碳排放地区绿色金融对GDP 碳排放强度的估计结果，从表中可以看出，低碳排放地区绿色金融对GDP 碳排放强度的回归系数为-11.4110，在5%的统计水平上显著，说明在低碳排放地区绿色金融可以十分显著的降低GDP 碳排放强度。由此，假说H1 在低碳排放地区得到验证。

表8 低碳排放地区系统GMM 的实证估计结果

从表8 中第（2）列可以看出，低碳排放地区绿色金融对GDP 碳排放强度的回归系数为-15.7857，在10%的统计水平上显著；能源结构对GDP 碳排放强度的回归系数为-3.5943，在5%的统计水平上显著。从表中第（3）列可以看出，绿色金融与能源结构的乘积项对GDP 碳排放强度的回归系数为-12.4215，在5%的统计水平上显著，说明能源结构的调节效应存在。同时，绿色金融对GDP 碳排放强度的回归系数为-3.6973，在10%的统计水平上显著；能源结构对GDP 碳排放强度的回归系数为-9.4275，在10%的统计水平上显著。说明在低碳排放地区通过能源结构的调节效应增强了绿色金融对GDP 碳排放强度的抑制作用。由此，假说H2 在低碳排放地区得到验证。

从表8 中第（4）列可以看出，低碳排放地区绿色金融对GDP 碳排放强度的回归系数为-10.3427，在10%的统计水平上显著；绿色全要素生产率对GDP碳排放强度的回归系数为-1.2607，在10%的统计水平上显著。从表中第（5）列可以看出，绿色金融与绿色全要素生产率的乘积项对GDP 碳排放强度的回归系数为-17.0520，在5%的统计水平上显著，说明绿色全要素生产率的调节效应存在。同时，绿色金融对GDP 碳排放强度的回归系数为-7.3421，在5%的统计水平上显著；绿色全要素生产率对GDP碳排放强度的回归系数为-8.5866，在5%的统计水平上显著。说明在低碳排放地区通过绿色全要素生产率的调节效应增强了绿色金融对GDP 碳排放强度的抑制作用。由此，假说H3 在低碳排放地区得到验证。

（三）稳健性检验

本文采用更换估计方法和改变样本容量的方法进行稳健性检验，得出的稳健性检验回归结果与前文结论基本一致，说明本文的结论是较为可信的。由于篇幅限制，表未列出。

六、研究结论与政策建议

（一）研究结论

通过本文的研究得出以下结论：

一是绿色金融可以显著的降低GDP 碳排放系数，即绿色金融可以助力经济低碳转型。在当前的能源结构和绿色全要素生产率水平下，绿色金融可以同时通过能源结构和绿色全要素生产率的调节作用助力经济低碳转型。

二是能源结构和绿色全要素生产率对绿色金融助力经济低碳转型的调节机制存在区域异质性。在高碳排放地区能源结构和绿色全要素生产率的调节机制没有发挥出来；在低碳排放地区能源结构和绿色全要素生产率在绿色金融助力经济低碳转型中的正向调节机制都得到了发挥。

（二）政策建议

首先，强化绿色发展理念，积极完善绿色金融体系。绿色金融是实现经济低碳转型不可或缺的重要力量，应积极推进绿色金融的发展，一方面，要强化绿色发展理念，创新绿色金融产品，将金融产品设计逐渐向清洁能源拓展。另一方面，还应尽快完善绿色金融体系的建立，积极引导不同类型的金融机构渗透到绿色金融的发展当中，鼓励并引导证券、基金、信托等其他金融机构在绿色金融发展中发挥积极作用。

其次，加快清洁能源开发，促进能源消费结构低碳化。能源结构在绿色金融助力经济低碳转型过程中发挥着重要的调节作用，虽然我国已经开始关注对能源结构的调整，但由于能源禀赋的差异，不同省份的调整效果还存在不小差异。我国应充分利用两个市场、两种资源，鼓励各行各业使用天然气等清洁能源，降低对化石能源的依赖，优化一次能源消费结构，支持新能源产业的发展，积极推进能源结构调整，进一步实现能源利用的高效化、清洁化。

最后，提高技术创新水平，促进经济增长方式向集约型转变。绿色全要素生产率同样在绿色金融助力经济低碳转型过程中发挥着重要的调节作用，绿色全要素生产率的提升离不开技术创新水平的提高。各个省份应高度重视技术创新，一是加强开发和推广节能降耗技术，降低行业企业的综合能耗水平。二是要制定低碳技术创新发展战略，鼓励低碳技术的研发和应用，建立低碳技术创新和共享平台，提升企业在低碳技术创新方面的竞争力。