基于熵值法-固定比例技术的机场运营效率计算新方法

于 剑，窦一梅

0 引 言

机场运营效率的评估是近年来重要的研究领域。通过机场运营效率评估，航空公司可以更好地了解高效机场，在合作时掌握先机。机场运营商可以依据运营效率结果更好地认识自身特征，了解在行业中的地位以及需要改进的方面。例如效率低下的机场通过选择高效率机场进行合作来提高运营效率。政策制定者则可以通过机场运营效率值决策新形势下的合作伙伴关系等。在这样的背景下，科学衡量机场运营效率，对于实现机场可持续发展、提升竞争力具有重要意义。

数据包络分析（DEA） 是目前机场行业应用最广泛的运营效率分析方法。Yongrok Choi[1]使用SBM-DEA 模型考察2016—2019年中国37 个主要机场的运营效率，解决了传统DEA 模型只采用径向方法，不能考虑松弛，导致估计过高，辨别能力较弱的情况。部分学者认为，传统的DEA方法对相关输入和输出变量的识别非常敏感，需要随着输入和输出变量数量的增加而增加有效决策单元的数量。此外，它也没有提供一个合适的有效决策单元排名列表。Santonab Chakraborty[2]对此提出将最优最劣方法（BWM） 与多属性边界近似区域比较法（MABAC） 技术结合起来，解决传统DEA的局限性，得出了印度32 个主要国际机场的排名名单，确定了每个机场的相对优劣势。在传统DEA方法中，决策单元（DMU） 可以被认为是完全有效的，“当且仅当其投入或产出能够得到改善，而不影响其他投入或产出”，这个定义意味着输入和输出参数可以互相替换。Barnum 等人[3]指出，如果投入/产出不能被替代/转换，那么在DEA方法中将无法正确地估计替代/转换的边际率。这种情况导致DEA形成不正确的等量/生产前沿，产生有偏的效率分数（Gleason 等[4]；Barnum 等[5]）。

在机场运营效率研究中，分析模型指标中包括不可替代的投入即航站楼面积、跑道系统、劳动力、运营成本和不可转换的产出即乘客、货运、飞机、收入。这些不可替代/不可转换的输入/输出在机场生产系统中不能相互替代，因此，机场生产系统大多采用固定比例的技术。然而，这一问题在机场运营效率研究文献中很大程度上被忽略了，广泛应用的是DEA，该方法假设输入之间有替代，输出之间有转换[6]。在许多情况下，违反这一假设会导致DEA结果的偏差，进而导致机场实践中的错误管理决策。

为了解决这个问题，本文提出了熵值法-固定比例技术（EFPR） 的运营效率指标计算方法，证明了在输入和输出不可替代时，传统DEA的运营效率估计是有偏差的，同时该方法可以更精准识别高效机场，检验机场生产系统的异质性。

1 EFPR 研究方法及模型构建

1.1 EFPR 方法

熵值法-固定比例技术，其中固定比例技术（FPR） 是一种用于输入不可替代、输出不可转换情况下的效率分析方法。通过熵值法来定义FPR计算中每个标准的优先级权重，并检验机场生产系统的异质性，利用该方法，来测量机场的个体表现差异。

FPR的主要特点包括以下几点：FPR中包含了技术效率和规模效率，在每次投入过剩和产出不足时，FPR的测度都是单调递减的。此外，FPR封装了数据，被评估的决策单元（DMU） 的每个单独比率与该特定输出/输入对的最大比率进行比较，该最大比率相对于最有效的输出/输入对产生其效率。之后，将每个DMU 的单个比率的平均值与最大平均值比率进行比较，这产生其相对于最大平均效率的个体运营效率。因此，该公式符合DEA惯例，即效率基于被分析的单元集合中最有效的观测值。另外由于公式构造的性质，很容易确定所评估的DMU 的输出/输入对中的哪些是低效率的来源。

FPR模型的主要目的是在输入（或输出） 不可替代的情况下，识别传统DEA模型中的偏差。这个模型保留了许多DEA模型的特点，可以使用相同的变量作为输入，并使用相同的指标来衡量效率水平。它们之间的唯一区别是决策单元能否被认为是有效的点。因此，两种方法的结果可以直接进行比较，并可以确定它们效率估计的真正差异。另外，FPR是目前可用于与传统DEA进行比较的最有效措施。考虑实际生产生活中投入产出的不同重要性，引入熵值法提供权重系数。

1.2 EFPR 模型建立

首先，建立决策矩阵以式（1） 的形式收集熵的输入数据，即投入数据和产出数据分别收集。

式中：Xi（j）为第j个投入产出指标所对应的第i个机场中的数据。

接下来是指标归一化处理，主要是对上面的矩阵进行标准化，计算ri（j），为消去量纲，需要对初始数据标准化，一般所选的标准化法为离差法。

如果j是正向属性：

如果j是负向属性：

其中投入指标使用负向属性公式，产出指标则使用正向属性公式进行计算。

最后，使用式（4） 计算所有标准的熵：

λ 是波尔兹曼常数，λ=1/lnn。这可以保证0≤Hj≤1。

通过式（5） 提供指标信息的多样化程度Hj：

根据式（6） 计算j指标的熵权wj：

可以得到W=（w1,w2,w3,…,wj），其中

投入和产出的参数应分别遵循这些阶段。从熵值法过程中获得指标的优先权重将纳入固定比例技术的模型。FPR的建立步骤如下：

对于每一个决策单元的相对效率：

式中：effkmn表示决策单元k即机场的运营效率得分，ykn为DMUk的一次输出，xkm为DMUk的一次输入，yjn为DMUj的一次输出，xjm为DMUj的一次输入。其中FPR公式中被除数是DMUk的所有标准化输出与所有标准化输入的比率之和，而除数是最有效的DMUk的所有标准化输出与所有标准化输入的比率之和，是DMUk的效率与最有效的DMUj的比率。因此，DMUk的得分在0 到1 之间，而效率最高的DMU 得分为1，表明效率为100%。需要特别注意，FPR在其一般形式中对每个输入/输出参数假定相等的权重。为了适应熵值法过程vi和ur得到的优先权值，将FPR的一般形式推广为式（9） 和式（10）：

2 案例结果及分析

在利用EFPR模型进行机场运营效率计算之前需要机场投入产出指标。本文重点研究我国40 个繁忙机场2015 年至2019年间的运营效率，选取航站楼面积和跑道长度作为本文的投入指标[7-10]，其中航站楼不仅是旅客购票、休息就餐及行李搬运的主要场所，而且航站楼的大小可以很好地反映机场所使用的实体资本，如登机口、登机柜台等。跑道作为航空运输的重要组成部分之一，跑道长度可以决定降落的飞机类型，同时可以决定机场的总体容量。当机场具有多条跑道时，跑道长度相加作为总的跑道长度。产出指标则选择旅客吞吐量、货邮吞吐量以及起降架次，三个指标显示了机场在当前输入的情况下有多大的潜力。机场相关的数据来自每个机场的网站、机场统计公报。

2.1 熵值法权重分析

熵值法第一部分是组成决策矩阵X，之后组合归一化决策矩阵，得到各参数的标准差。跑道长度和航站楼面积的标准差分别为0.237 1 和0.203 0。这些结果表明，跑道长度具有更强的对比强度。旅客吞吐量、货邮吞吐量和起降架次的标准差分别为0.215 2、0.188 0 和0.237 1，表明起降架次是输出参数中差异性和对比度最高的数据。

表1 为输出变量构造的线性相关矩阵，数值大小表示线性相关程度。结果表明，旅客吞吐量与起降架次间有很强的相关性。此外，与起降架次相比，旅客吞吐量与货邮吞吐量的相关性更高。结果表明，旅客吞吐量数据是最一致的数据，货邮吞吐量数据是最不一致的数据。

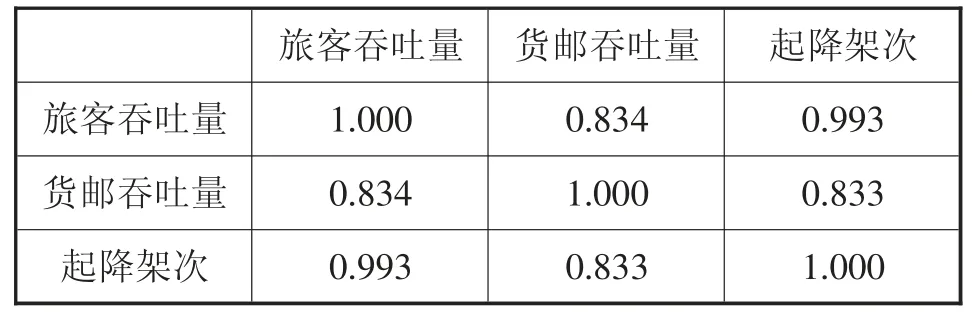
表1 输出指标的相关性

利用式（4） 计算每个输入输出参数所携带的信息量（Hj），跑道长度值为0.988 7，航站楼面积值为0.990 9。旅客吞吐量、货邮吞吐量、飞机起降架次的Hj值分别为0.955 8、0.927 9、0.956 7。利用相关矩阵和式（5） 计算输入和输出的差异度。跑道长度和航站楼面积值分别为0.011 2 和0.009 1。其两者差异并不大，但输出参数的值存在差异较大，旅客吞吐量、货邮吞吐量、起降架次的值分别为0.044 2、0.072 1、0.043 3。因为指数表示每个指标标准的差异，很明显，货邮吞吐量是占权重最大的输出参数。基于2019 年数据，跑道长度和航站楼面积的最终优先级权重是0.545 9 和0.454 1，客、货吞吐量和飞机起降架次的优先权重是0.277 1、0.451 8 和0.271 1。

图1 显示了2015 年至2019 年的标准权重。在输出方面，机场货物处理量不均衡，部分机场在货物运输方面与其他机场有较大差异。但自2015 年以来，货物运输差异逐渐增大，而客运运输的差距在进一步缩小。这意味着在2015—2019 年间，货物运输的竞争有所上升。另一方面，旅客吞吐量以及起降架次权重的降低表明同一时期中国各机场差距变小，这些参数对机场运营效率的影响也在减小。

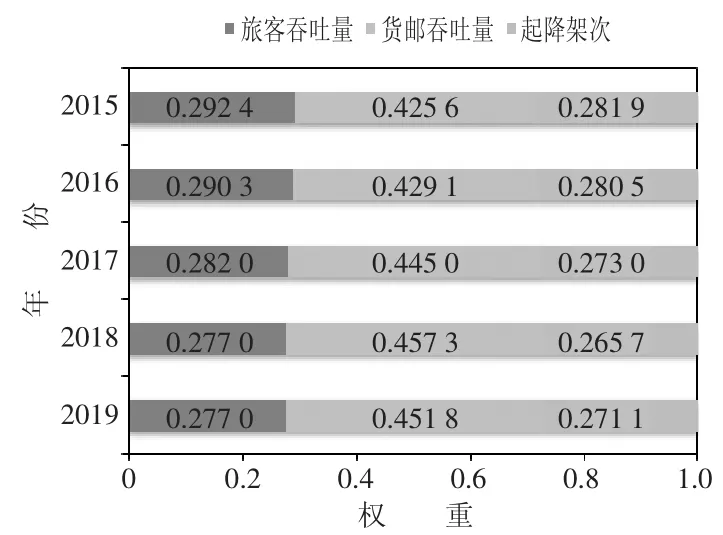
图1 输出指标2015—2019 年标准权重的变化

2.2 EFPR 计算结果分析

从熵值法计算中获得的优先级权重适用于EFPR过程。本文认为输入（航站楼面积和跑道长度） 是不可替代的，输出（旅客吞吐量、货邮吞吐量和起降架次） 是不可转换的。通过构建EFPR模型来分析中国机场的运营效率。该模型包括两个输入和三个输出指标。40 个机场的运营效率结果如图2 所示。

根据运营效率结果，北京首都国际机场在模型中处于高效地位。平均效率水平在0.43~0.55 之间波动，在2019 年达到顶峰。北京首都机场连续5 年被认为是具有充分高运营效率的机场。除此之外，厦门高崎以及成都双流机场平均效率得分最高，分别是0.81 和0.77。拉萨贡嘎机场是最低效的机场，平均效率仅有0.12，同时也是数据集中最低效的机场。

2.3 EFPR 模型对比分析

由于货邮吞吐量是代表机场异质性的输出参数，这一部分探究去除货物吞吐量指标后影响的机场运营效率。排除货邮吞吐量后，可以看到旅客吞吐量和起降架次之间权重更加均衡，如图3 所示。

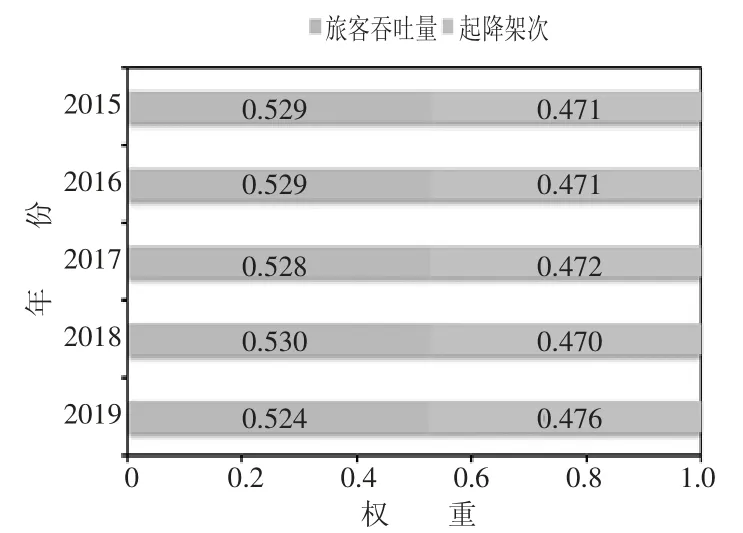
图3 输出指标2015—2019 年标准权重的变化（不含货邮吞吐量）

无货邮吞吐量的机场运营效率如图4 所示，平均效率在0.43~0.56 之间浮动，同样在2019 年达到最高峰。机场平均效率除了北京首都机场外没有效率级别为1 的机场。其中，去掉货邮吞吐量指标后，部分机场运营效率值下降，如上海浦东国际机场，由原来的0.65 下降到0.63，这个结果则是浦东机场的货邮吞吐量处理量较大所导致的。与此同时，一些注重客运业务的机场则运营效率提升，如三亚凤凰和哈尔滨太平机场。

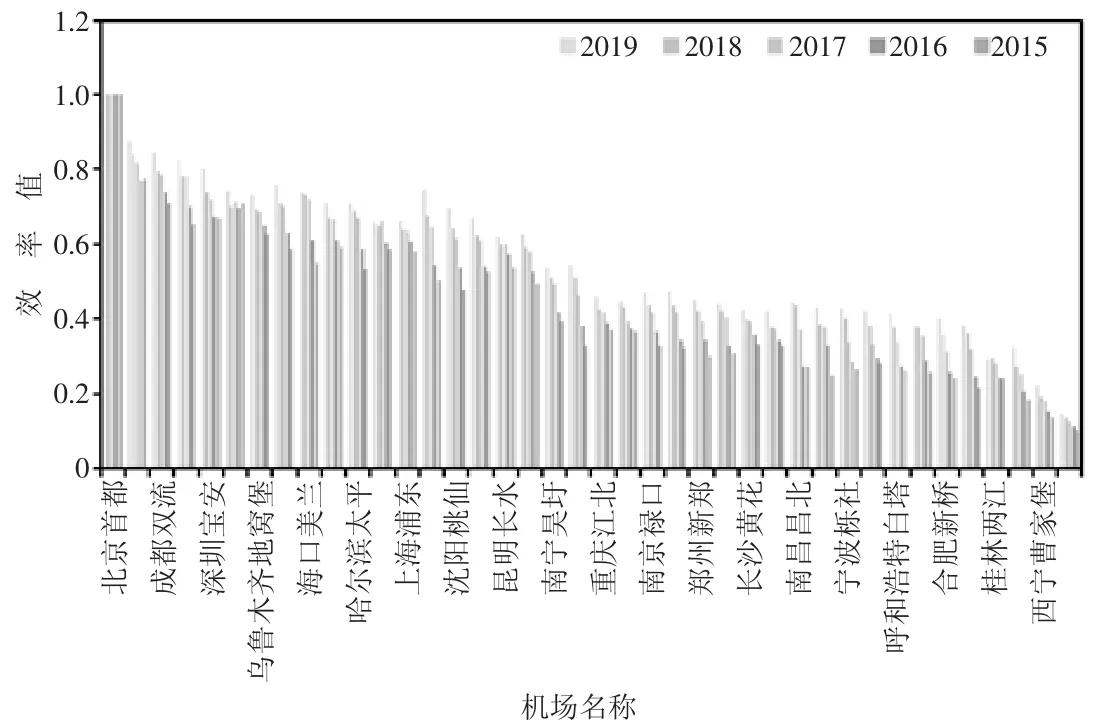
图4 EFPR 模型计算的中国机场运营效率（不含货邮吞吐量）

同传统DEA方法结果相比较，两种方法产生的得分之间存在显著差异，因为FPR不具备尺度效应，因此EFPR平均产生的运营效率得分较低，如图5 所示。高效机场数量变少。EFPR模型仅识别出一个高效机场，而传统的DEA则识别出4 个完全高效的机场。这表明，提出的方法可以减少效率值为1 的机场的数量，这更加符合实际生产中的结果，提高了效率计算的精准度。使用该方法可以避免将一些低效机场归类为高效机场，从而减少错误的管理决策。

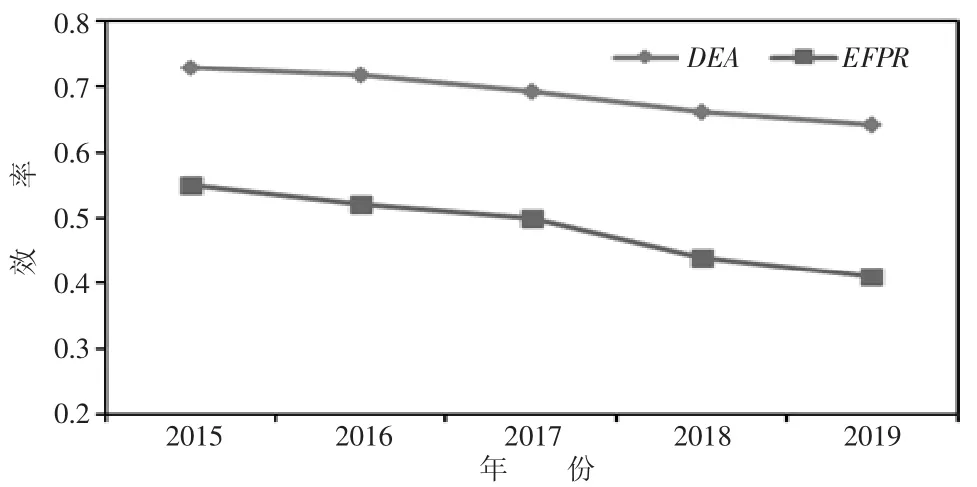
图5 传统DEA 方法中运营效率的偏差

3 结 论

机场生产系统大多由不可替代的投入和不可转换的产出组成，因此受到固定比例技术的制约。在效率分析时应考虑系统的这一特点，在使用需要输入/输出参数之间进行替换/转换假设的DEA等方法时应谨慎。否则，可能会获得偏倚的效率得分，从而导致错误的管理决策。

本文提出了一种新的组合EFPR方法来进行效率比较分析，实现了对机场运营效率的稳健分析，并为机场行业提供了不同的见解。该方法被应用于2015 年至2019 年5 年间中国主要机场的运营效率分析。对机场的个别表现的变化进行了展示，此外，与传统的DEA方法相比，该方法减少了有效机场的数量，实现了较高的区分度，且具有更强的鲁棒性。