一种改进非线性模型预测轨迹跟踪控制方法研究
2023-12-12李文超刘美如
李文超,刘美如,丁 华,梁 军,张 春
(1.江苏大学 汽车与交通工程学院, 江苏 镇江 212013;2.江苏大学京江学院, 江苏 镇江 212013;3.江苏大学 汽车工程研究院, 江苏 镇江 212013;4.宝胜系统集成科技股份有限公司, 江苏 扬州 225800)
0 引言
随着社会的快速发展,汽车保有量大幅上升,进而导致交通拥堵愈发严重,交通事故频发。为缓解目前交通的拥堵现状,提高行车效率与安全性,智能辅助驾驶技术成为当下的研究热点[1]。目前,对智能辅助驾驶技术的研究主要包括环境感知、决策、规划与控制等方面。其中,轨迹跟踪控制是车辆控制的重要部分[2]。在狭窄场景中,车辆运动空间有限并与障碍物距离较近,容易在车辆行进过程中造成擦碰。因此,进行精准且稳定的车辆控制是智能辅助驾驶技术的重中之重。
当前,智能车辆轨迹跟踪控制大致可分为传统的控制方法以及最优控制方法。传统的控制方法主要包括预瞄驾驶员模型[3-5]、PID控制[6-8]以及滑模控制[9-11]等。Chen等[12]设计了一种BP神经网络和PID控制相结合的控制方法并利用遗传算法(GA)优化BP神经网络,从而提高了系统的鲁棒性以及收敛精度与速度。Wu等[13]结合滑模控制和模型预测控制,提出了一种鲁棒的滑模预测控制器,确保系统在各种约束下性能控制最优,从而提高智能车辆实时路径跟踪性能。然而,PID是一种无模型的控制方法,在一些复杂、非线性场景下,其跟踪精度较低。同时,滑模控制对于复杂系统的不匹配干扰处理较为困难,难以设计其稳定性趋近率,因此不能达到很好的跟踪效果。
最优控制方法一般包括模型预测控制(MPC)[14-18]以及非线性模型预测控制(NMPC)[19-22]两类。目前,模型预测控制方法具有较好的控制效果。该方法允许模型存在误差,并能够通过修正预测模型来有效处理模型适配、干扰引起的系统不稳定问题。因此,基于MPC的车辆跟踪控制是当前的研究热点之一。狭窄车位条件下,为了确保可靠的防碰撞动作,MPC在很大程度上取决于所构建的车辆模型[23]。非线性车辆模型可以为控制开发提供更好的车辆模型[24]。针对泊车参考路径的曲率和航向角较大等问题,Yin等[25]提出采用离散的预览点进行路径跟踪的非线性模型预测控制,并采用车辆位置与预览点切线的垂直距离来评估跟踪误差。采用线性化模型作为预测模型会导致跟踪误差较大[26],而采用非线性预测模型可以提高预测时域内估计值的准确性,但相对前者其计算复杂度增加。非线性预测模型的使用会导致严重的计算负担,进而难以保证其控制的实时性。针对上述非线性预测模型应用中存在的局限性,Chen等[27]提出一种基于开放封闭原则(OCP)稀疏结构的压缩算法,在压缩离散化节点数方面,实现了由二次压缩转换至线性压缩,进而降低了其计算复杂度。Son等[28]提出了利用移动分块MPC的半显式方法来解决一个简化的在线优化问题。该方法虽然通过离线来求解出分块位置,但仍为固定矩阵分块的方法,难以很好的优化一个动态过程。因此,本文中提出了一种改进的NMPC控制器设计方法,用于车辆在狭窄车位下的非线性轨迹跟踪控制。
1 非线性预测模型建模
非线性模型预测控制方法通常将输入量和状态量一同作为决策变量,将模型的状态方程作为非线性约束,再根据实际情况构建目标函数。然后,对该目标函数进行最优化求解,得到最优控制量作用于被控系统,进而车辆依据函数输出量做出航向调整的一个循环推进的过程。在狭窄停车场环境下,车辆行驶以及倒车入库过程中容易发生车头或车尾擦碰,为提高车辆行驶和泊车的安全性,需要搭建较高精度的车辆模型。因此,本节针对车辆前进和倒车2种运动方式,分别搭建了相应的预测模型,并采用改进的二阶龙格库塔方法对其进行离散化处理,以提高轨迹跟踪精度。
1.1 简化的运动学模型
泊车是一个低速行驶的过程,此时认为4个车轮是纯滚动的而不发生滑移现象[29-30]。一般而言,车辆形状大多具备非线性特性,难以对其做到精确建模[31]。因此,本文中将模型简化,将四轮模型简化为二轮模型以构建车辆运动学模型,如图1所示。
[xyφ]T=[cosφsinφtanδf/l]T*ds
(1)
式中:φ航向角为X轴与车轴线的夹角;(x,y,φ)为车辆的状态量;r和f为车辆后轴与前轴中点;l为车辆轴距;δf为前轮转角, ds表示在dt时间内走过的距离。
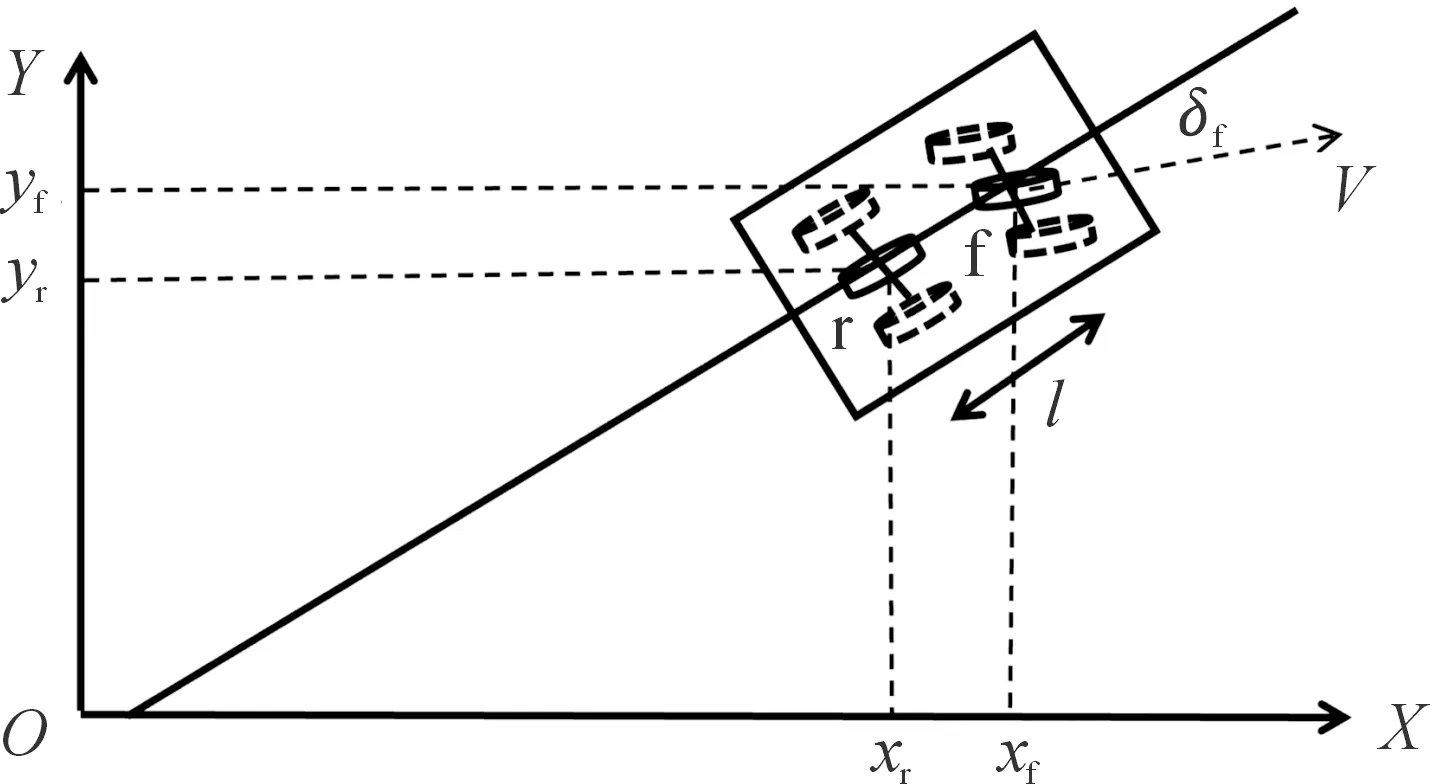
图1 简化的车辆运动学模型
1.2 车辆前进运动学模型建模
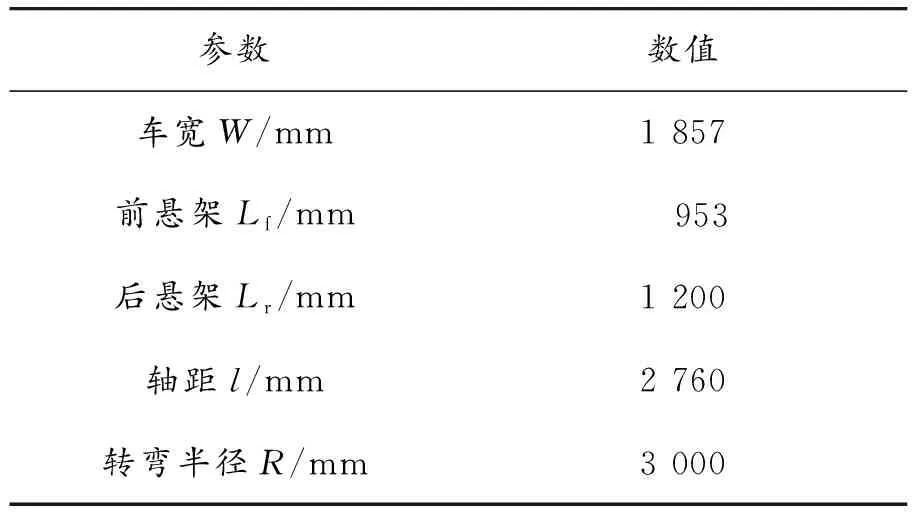
为增加预瞄点位置的精确性,在模型搭建过程中将原本单一采样时间转换成可变采样时间T(k)(1 ds=v*dt=v*T(k) (2) 针对狭小停车空间场景,为了确保车辆实现可靠的防碰撞动作,需要对车辆进行较高精度的分析,搭建更贴合实际的车辆模型。因此,采用龙格库塔(Runge-Kutta)的内迭代法来有效提升建模精度。RK方法是通过计算若干采样点的斜率来构建更高精度的积分计算,利用泰勒级数展开进行数值求解[32]。 (3) (4) q1=f(x,y) (5) (6) 通过式(4)—式(6)对车辆的横、纵坐标以及航向角进行离散化处理: 式中,k=0,1,2,…,Np-1。Np为预测时域。 每次采样时车辆的当前状态有横坐标xk,纵坐标yk,航向角φk,前轮转角δk。若已有一组控制序列[δ1,δ2,δ3…δn],代入式(7)便可得每个采样时刻的航向角,继而获得相应的横、纵坐标,从而预测到未来的节点状态。 对于车辆倒车运动,车速极低,因此视车辆后轴纵向速度为0,满足: (8) 前轴中心点(xf,yf)的位置关系为: (9) 将式(9)求导并代入式(8),且X轴与vf的夹角为φ-δf,因此倒车运动学模型为: [cos(φ-δf) sin(φ-δf) -sinδf/l]T*v (10) 同理,进行离散化处理可得: (11) 根据车辆3自由度运动学模型,选取当前车辆横坐标、纵坐标、航向角、纵向速度,参考路径的横坐标、纵坐标、航向角为输入参数,前轮转角为输出参数。 滚动优化是一种通过最优相应时刻的性能指标,比如最小误差、最小控制能量等来获得系统最优控制输入的方法。该方法的核心为在采样周期内考虑车辆当前状态,在线滚动式求解有限时域内的开环最优问题,得出最优控制序列,并将该控制序列的第一个变量作用于被控系统,使得控制系统在下一采样周期既有前馈补偿又有当前状态量的反馈补偿,从而提升车辆控制的精确性。 移动分块策略是一种针对最优控制问题降低目标函数输入量自由度的优化方法,即在预测范围内采用固定分块模式优化输入量来降低控制器求解的复杂度[33]。该方法通过块约束目标函数的输入量,来减少优化求解中独立的变量个数以降低控制器的计算负担。非线性模型预测控制方法只将控制增量序列的第一个元素作用于系统,因此本文采用移动分块矩阵对控制增量进行块约束,以实现精确计算第一个元素而模糊计算其他元素,减少独立输入量,降低计算负担。目前来看,车辆控制方面利用移动分块矩阵的研究较少,主要为“平均化”矩阵和“前疏后密”矩阵。进一步的,相关的研究大多未考虑到非线性因素,难以保证研究的可行性。因此,本文基于非线性模型预测控制方法,利用大量试验来确定移动分块矩阵。 移动分块策略采用较小的块对前端的控制变量进行约束以保证轨迹跟踪的精确性,采用较大的块对后端的控制变量进行约束以降低最优化函数的求解复杂度。在本文中,ΔUk为控制范围内的控制输入序列,其值越小表示车辆的实际坐标离参考坐标越近,跟踪效果越好。控制增量ΔUk定义为: ΔUk=[ΔukΔuk+1… Δuk+Nc-1]T (12) 选取式(12)控制增量序列的第一个元素作为实际控制增量输入,作用于被控系统,则系统实际的控制量uk为: (13) 在下一控制周期,同步向前推进优化时段,从而实现最优控制问题的在线滚动计算。 式(12)中,控制时域Nc=9,待求解的独立控制量数目为9。随着Nc的值增大,控制器的轨迹跟踪精度也逐渐升高,但控制器优化时计算量急剧增加。因此,提出独立控制增量ΔUn,其为通过块约束形式对控制增量ΔUk进行简化,ΔUn形式如下: ΔUn=[Δu1Δu2… ΔuNd]T (14) 式中,Nd ΔUkn=G*ΔUn (15) 式中:ΔUkn为分块矩阵约束后的控制增量;ΔUn为独立控制增量;G为分块矩阵,矩阵规模为Nc*Nd,其功能是缩减独立控制量个数。该矩阵的取值形式随分块方法不同而不同,Abdul等[34]将Δu5之后控制量都取相同的值,G取值如下: 以该取值形式的分块矩阵为例,对原始的控制增量进行块约束后得到ΔUkn的形式如下: (16) G将Δu5、Δu6、Δu7、Δu8、Δu9约束成相同的值,自由度由9降低至5,从而节省计算成本。然而,此类固定分块方法只能有限的降低求解负担,还会导致块约束后的输出值不能很好反应原本的控制量,产生较大的偏差。针对该方法存在的局限性,本文提出改进的移动分块策略,即采用一个动态的移动分块矩阵集合Gi,i=1,2,3,4,对控制量滚动式约束。Gi取值如下: 动态移动分块矩阵选取原则: (17) 按照上述原则选取相应的分块矩阵。首先,采用G1矩阵,使得Δu2=Δu3=Δu4=Δu5=Δu6,即降低了目标函数输入为Δu3至Δu6时刻的求解复杂度;在当前目标函数求解周期中,当采样时刻k=3,即求解第三个采样点的最优解时刻,转而采用G2矩阵,使得Δu3=Δu4=Δu5=Δu6=Δu7,从而降低代价函数输入为Δu4至Δu7时刻的求解复杂度。同理,采用G3、G4矩阵相应降低后续元素的求解复杂度。综上,在优化目标函数输入量方面,将原来的固定移动分块矩阵转为控制器一次求解周期里的四次矩阵,即在目标采样点求解时采用相应的分块矩阵,继而循环推进该四次矩阵,对控制量进行滚动约束以提升控制器的求解效率。因此,与ΔUk相比,通过改进后获得的ΔUkn无需在每个变量处进行优化求解,其控制变量自由度的减少降低了控制器的求解负担,提高了求解效率。 根据上述非线性预测模型及分块策略,综合考虑车辆行驶的跟踪性能与平稳性,最小化位置误差、航向误差以及前轮转角增量,在每一个步长内最优化目标函数。构造的优化函数如下: (18) 受车辆自身条件限制,在路径跟踪控制器的优化求解问题中,参数取值存在范围约束。若参数取值超出车辆的限制条件则易导致危险事故发生,因此需要对车辆部分参数进行如下约束: (19) 上述优化模型针对的是带约束的非线性优化问题,本文采用Matlab非线性求解器对该模型进行优化求解。 为了验证控制器的跟踪性能,基于Carsim与Matlab/Simulink搭建平台进行仿真实验,实验场景为小型停车场,考虑安全因素,设置车辆速度限制为3.6 km/h。本文首先基于Carsim搭建整车模型并导入至Matlab/Simulink仿真平台,车辆部分参数如表1所示。 表1 车辆部分参数 本研究针对狭窄车位进行仿真实验。在可泊车条件下,车辆一次性由前进挡转为倒车挡驶入车位到达目标点,此时存在一个空间约束,即最小泊车车位约束。通过分析车位的几何关系可计算得最小泊车车位的长度为4.992 m,宽度为2.045 m。进一步的,考虑到实际城市内常见狭窄停车位的大小,本文将最小车位设置为5 m×2.5 m。另外,仿真实验以在停车场环境下采用混合A*规划的路径以及给定节点坐标的拟合路径作为导航参考路径,基于两类参考路径条件下评估控制器的跟踪精度与控制效率。 以参考路径为变量进行多次试验,参考路径有“厂”字形,双移线道路,弯曲形以及阶梯形等拟合路径和采用混合A*算法规划的路径。此处仿真工况为拟合的参考路径,将参考轨迹与采用2种不同的离散化方法获得的车辆实际跟踪轨迹进行对比分析,验证控制器的轨迹跟踪性能。如图2所示,相较于欧拉法离散车辆模型,本文中提出的基于改进二阶RK方法进行离散化的控制方法可以更加精确地跟踪参考轨迹,提高跟踪精度。 图2 轨迹跟踪效果 进行垂直车位泊车,往往需要倒车入库,现存的倒车技术仍存在诸多问题。本文中通过对倒车运动学模型建模并离散化处理,进而利用非线性模型预测控制来实现对车辆的控制。 图3中的3条轨迹(黑线)均采用混合A*算法规划产生。图3(a)表示不含倒车预测模型的NMPC控制器的跟踪效果。由图3(a)可知,在前进路段,控制器同样具有良好的跟踪效果。然而,在倒车路段,车辆仍是正向行驶,控制器并不能跟踪参考轨迹。针对此问题,本文增加对倒车轨迹预测运动学的建模,并基于NMPC控制器进行仿真试验。如图3(b)所示,针对同一参考轨迹,所提控制器可以实现很好的跟踪效果。如图3(c)(d)所示,进行多次仿真试验,所提控制器均能够实现良好的全程跟踪效果。 图3 前进加倒车入库效果 在跟踪双移线轨迹(图2(d))实验方面,图4为基于无矩阵、固定矩阵以及本文中提出的动态矩阵控制方法的单步节点运行时间的对比图。由图4以及表2可以看出,基于固定矩阵控制方法的运行时间提升27.57%,基于动态矩阵控制方法的运行时间提升了38.96%,采用动态矩阵对控制量进行约束得到的效果更为明显。 图4 控制器单步节点运行时间 表2 单步运行时间对比 基于本文中所提的控制方法进行轨迹跟踪,路径跟踪结果如图5所示。图5(a)(b)(c)分别为跟踪图3(b)(c)(d)的横向误差。在最大横向误差以及平均误差方面,所提改进方法表现更好,精度更高。 图6(c)为路径规划模块获得的轨迹4以及对该轨迹的跟踪效果。图6(a)和(b)分别为前馈PID控制器、原始NMPC控制器、预瞄NMPC控制器以及本文改进的NMPC控制器等4类控制器的航向误差和横向误差对比。从图6(a)(b)能够看出,本文改进的NMPC控制器的控制效果最好,跟踪精度最高。图6(d)表示跟踪轨迹4的单步节点运行时间,采用散点图可以明显的展示出时间的差异性。因此,相较于原始NMPC算法,本文提出的改进NMPC控制方法可以大大提高控制器的求解效率。 图5 横向误差对比 图7为跟踪梯形轨迹的控制器单步运行时间散点图。由图7可得,本文中所提出的控制算法大大提高了计算效率,降低了计算负担。 图7 跟踪梯形轨迹单步运行时间散点图 表3为3类控制方法的平均运行时间。由该表可知,相较于原始NMPC,本文中提出的控制方法就“厂”字形轨迹(图2(a))和梯形轨迹 (图2(b)),效率分别提高了9.9%、28.7%。 表3 节点平均运行时间对比 1) 针对小型停车场车辆运动空间狭小、停车难、易发生事故等问题,提出一种非线性模型预测控制方法,具有一定的可行性与实际意义。 2) 针对控制精度问题,基于NMPC控制方法,建立了车辆前进与倒车的运动学模型并采用改进的二阶RK方法对其进行离散化处理。 3) 针对计算负担问题,提出了一种动态移动分块矩阵策略对控制量进行模糊-精确约束,以减少独立输入量的数目,从而提高求解效率。 4) 移动分块矩阵虽然可以降低目标函数的求解复杂度,但是也会影响控制器的吸引域(ROA),使系统难以稳定以致无法求解。本文中并未考虑到其递归可行性,未来研究将考虑系统稳定性等多方面的影响因素,选择更合适的块结构以提升控制器的求解效率。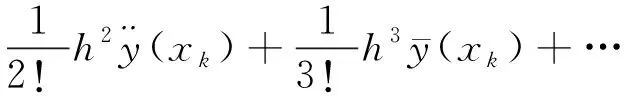
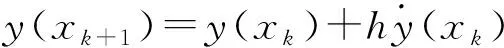
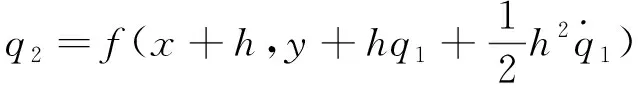
1.3 车辆倒车运动学模型建模
2 滚动优化
2.1 动态移动分块矩阵策略
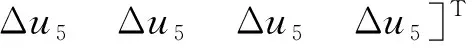
2.2 目标函数与约束条件

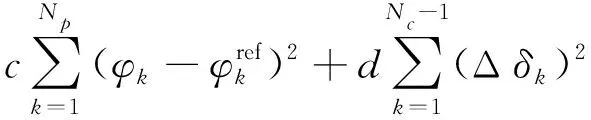
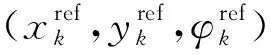
3 仿真计算分析
3.1 多种前进轨迹跟踪效果
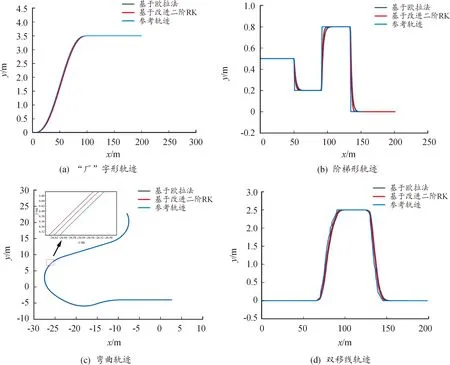
3.2 包含倒车轨迹跟踪效果
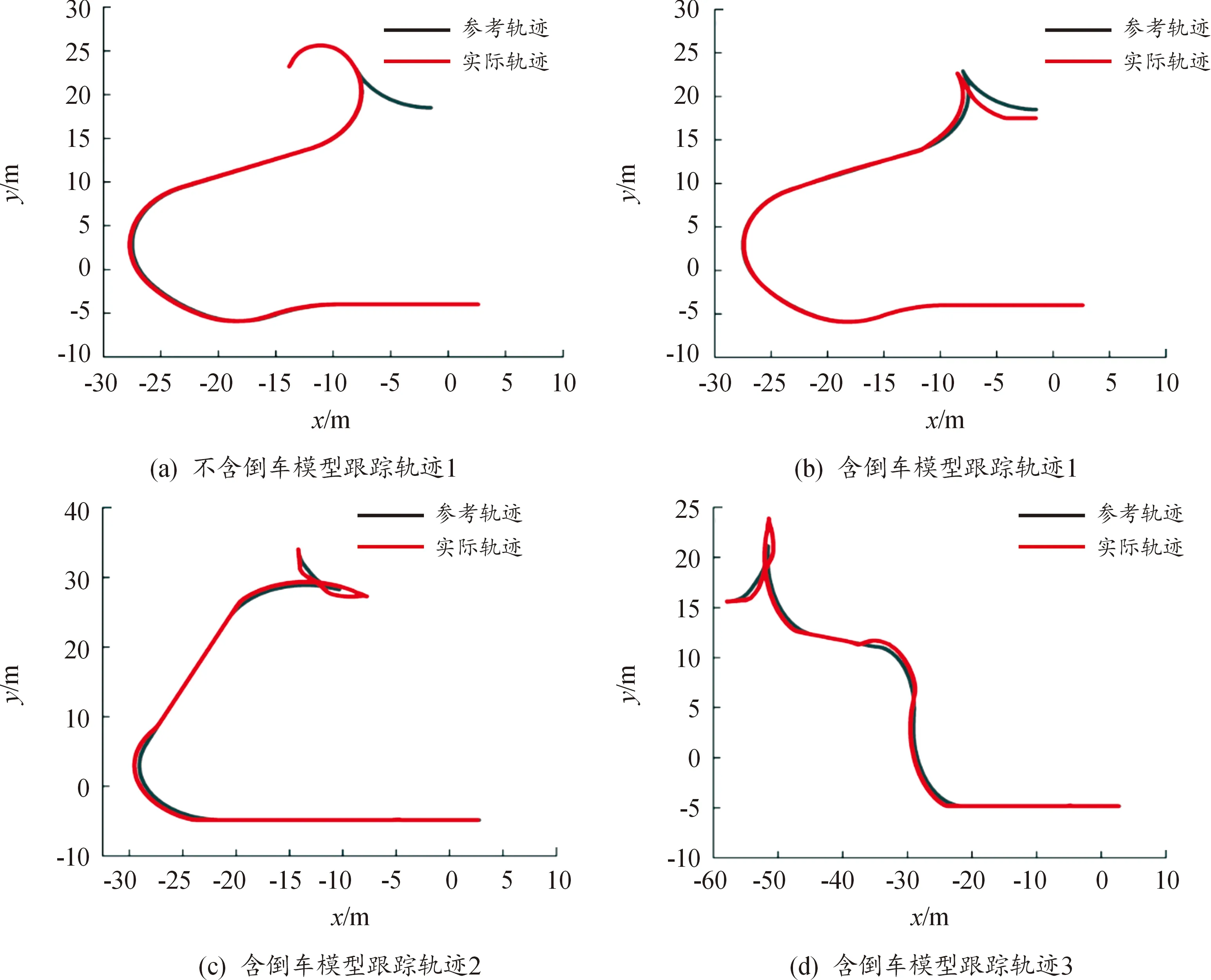
3.3 动态移动分块矩阵性能
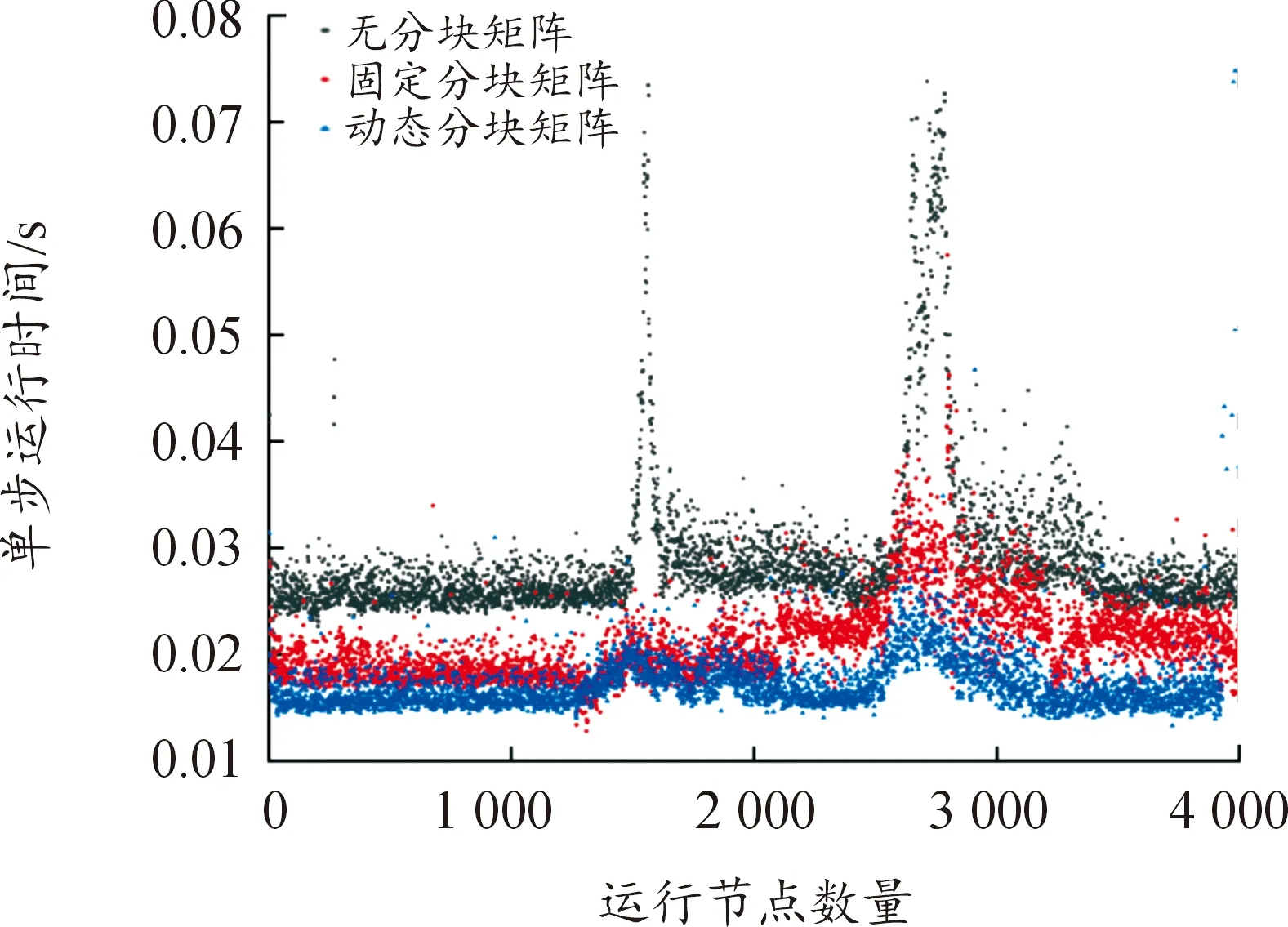

3.4 跟踪误差及效率

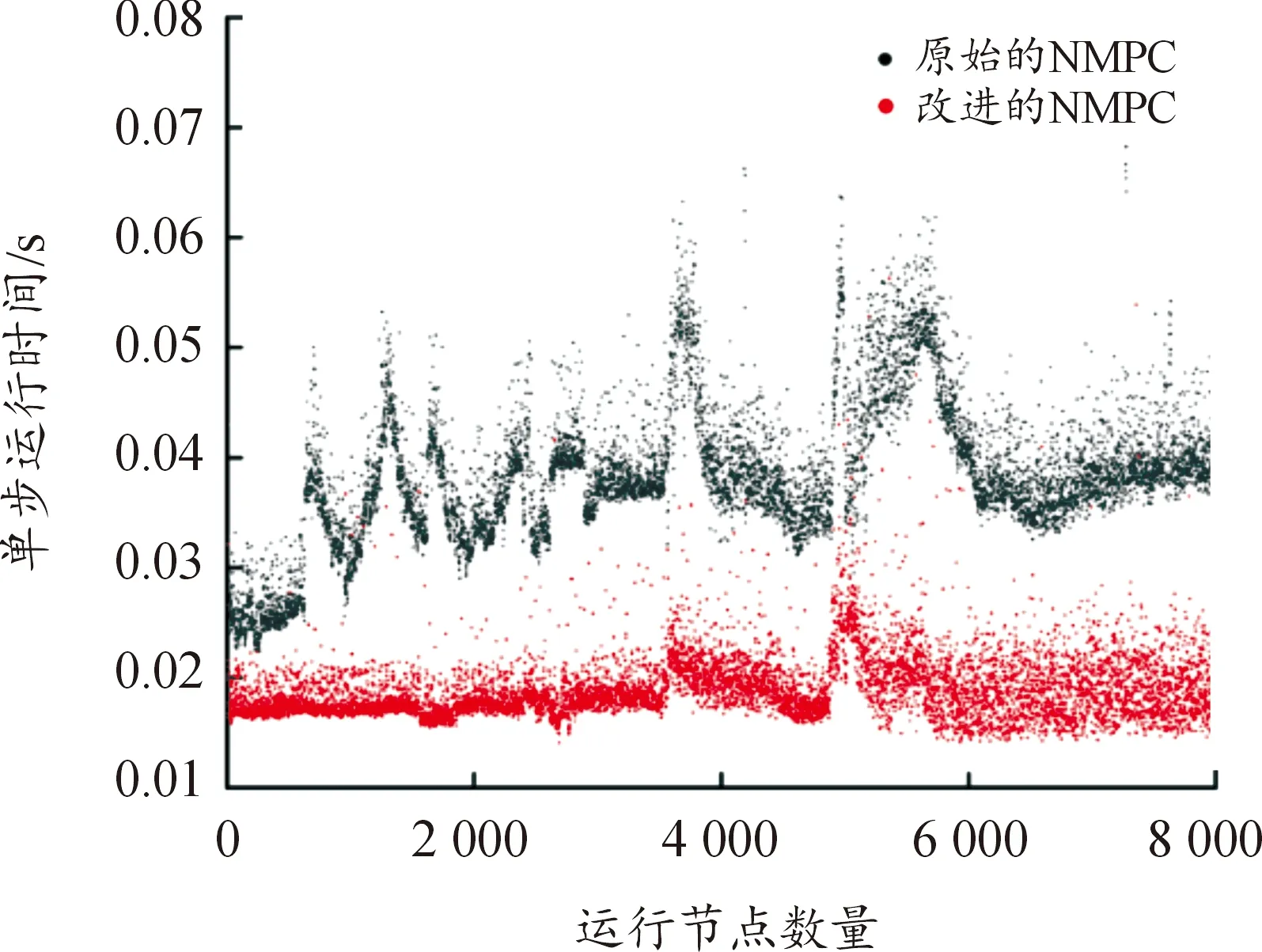

4 结论
