隧道支护设备机械臂运动学分析

陈世雨 任华 冯怀 杨伟

摘要：隧道建设中隧道支护为关键工序，针对需求国内大量公司研究所进行了其设备的研发，隧道内工况的复杂性，在产品设计好后需要验证其是否能满足施工和结构上的合理性，本次的产品结构新颖特殊集成多个功能，其操作控制难度高，故需要对其进行运动学分析。利用MOD_DH法确定两个工作系统的参数、坐标系建立正运动学方程，为灵活适应需求两个工作系统都为冗余机械臂，使用传统解析法求解逆运动学分析上存在困难，故本次利用遗传算法结合粒子群算法并加以改进，更好地满足逆运动学求解需求，利于蒙特卡洛和拉丁超立方抽样法进行设备工作空间的求解，然后在Matlab中进行仿真，结果表明该设备满足施工要求，但两个功能组不能同时工作，为后续的控制和结构改进提供了理论基础。

关键词：凿岩与拱架抓手機械臂；MOD_DH；工作空间；逆运动学；改进遗传粒子群算法

中图分类号：TP241 文献标志码：A doi：10.3969/j.issn.1006-0316.2023.11.009文章编号：1006-0316 （2023） 11-0062-10

Kinematics Analysis of the Mechanical Manipulator of Tunnel Support Equipment

CHEN Shiyu1，REN Hua1，FENG Huai2，YANG Wei1

（ 1.School of Mechanical Engineering， XihuaUniversity， Chengdu 610039， China;

2.Sichuan Lanhai Intelligent Equipment Manufacturing Co.， Ltd.， Chengdu 610039， China ）

Abstract：Tunnel support Tunnel support is a key process in tunnel construction. A large number of domestic companies and research institutes have carried out research and development of their equipment to meet the demand. Due to the complexity of working conditions in the tunnel， it is necessary to verify whether they can meet the construction and structural rationality after the product design is completed. Since The product structure is novel， special and integrated with multiple functions， it is difficult to operate and control it. Therefore， kinematics analysis is required. MOD_ DH method is used to determine the parameters and coordinate systems of the two working systems and establish the forward kinematics equations. In order to meet the requirements flexibly， the two working systems are redundant mechanical arms， and there are difficulties in inverse kinematics analysis. The traditional analytical method is not applicable. Genetic algorithm is combined with particle swarm optimization to better meet the requirements of inverse kinematics solution. It is convenient for the use of Monte Carlo and Latin hypercube sampling methods to solve the workspace. The result of simulation with Matlab show that the equipment meets the construction requirements， but the two functional groups cannot work at the same time. It provides a theoretical basis for subsequent control and structure improvement.

Key words：rock drilling and arch grab arm；MOD_DH；workspace；forward kinematics；genetic particle swarm optimization

国内隧道支护设备还处在研究阶段、功能单一等问题，且主要为单一功能设备的研究，对多功能一体化设备在运动学上的研究较少，工作空间以及运动学控制都存在一些问题。本次的分析对象智能供锚喷一体化台车，集成多种功能。本次分析其右臂架，集成凿岩与拱架安装功能，由于多功能的集成和高自由度造成控制困难高和工作空间不明确等问题，对其进行正运动学、逆运动学和工作空间验证，为后续结构设计改进提供理论基础，并且为后续的运动学控制提供理论基础。

机械臂正运动学建模常用的方法有Pro-E[1]和D-H[2]两种建模方法，正运动学一对一的映射关系，而逆运动学为一对多的映射关系[3]。常规的机械臂的逆运动学求解有封闭解法和数值解法[4]，两种方法对机械臂的结构或者自由度存在要求，且存在计算量大、模型建立困难计、算过程复杂等问题，为此将群智能优化算法引入到机械臂的运动学逆解中，其中主流的有遗传算法[5]、粒子群优化算法[6-7]、萤火虫算法[8]、人工蜂群算法[9]等，其中Cheng X和Zhao M[10]提出一种结合了量子蚁群算法和神经网络的MQACA-RBF算法提升运动学逆解位置精度。Dereli[11-12]提出利用两个改进粒子群算法求解七自由度串联机械臂和利用量子粒子群算法求解，并与标准粒子群、人工蜂群等算法求解效果进行比较，取得了更好的效果。石建平[13]对粒子群算法、克隆旋转选择算法和果蝇优化算法进行改进求解七自由度机械臂运动学逆解。

工作空间求解有数值法、解析法和图解法，解析法不直观而且自由度较少；图解法直接明了，但高自由度下需要复杂分组处理；数值法计算量大，边界曲线存在凹面时其准确性会下降[14-15]，因此统计学求解工作空间增多，主要有基于蒙特卡洛法[16]和基于拉丁超立方体抽样方法[17]，通过随机抽样的方法，来模拟机械臂在各种关节情况下的输出，当抽样数量足够多的时可以较为真实的反映实际的情况。

综上所述，本文选用MOD_DH法进行正运动学建模，为了更快和更精准的实现逆运动学求解，本文提出一种改进遗传算法和粒子群相结合算法，在几种不同约束情况下进行逆运动学求解。为解决工作空间求解分析困难问题分别使用蒙特卡洛和拉丁超立方抽样法对两个工作组进行工作空间求解，以此验证工作空间的正确性，分析工作空间上的问题，为后续的结构改进和运动控制提供理论基础。

1 机械臂运动学方程建立

本次分析对象凿岩与拱架安两个功能，故将其分解为凿岩机组与拱架抓手组两个串联机械臂。使用MOD_DH运动学建模，得到图1和图2两组连杆坐标系图（其中XYZ为坐标轴方向，下标为序号），得到两个机械臂MOD_DH参数如表1和表2所示，其中两组的前3个连杆参数一致，拱架抓手组为RRPPPRRRRRR型串联机械臂，凿岩组则为RRPPPRRPPP型串联机械臂。

旋转矩阵[18]如式（1）所示。

（1）

式中： 为旋转矩阵；Rot为矩阵之间的旋转变换；Trans为矩阵之间的平移变换； 、 为变换坐标轴； 、 为变换角度； 、 为移动距离；下标为序号；c代表cos；s代表sin。

依据式（1），通过上述矩阵之间的旋转Rot和平移Trans变换就可以得出机械臂各关节之间的齐次变换矩阵，将表1和表2中拱架抓手和凿岩机的MOD_DH参数代入式（1）可得到各个关节变换矩阵为：

（2）

（3）

式中： 为拱架抓手组第10个矩阵； 为凿岩机组的各关节齐次变换矩阵。

其余矩阵都为类似结果。根据链式计算法则，可以计算得出末端执行机构相对于基坐标系的位置与姿态，如此得到的齐次变换矩阵即为该机构的运动学方程：

（4）

拱架抓手组和凿岩机组的N分别为11和10；n向量表示末端执行端坐标系X轴相对于基坐标的旋转向量，同理，o向量与a向量分别表示末端执行端坐标系Y轴与Z轴相对于基坐标的旋转向量，而p向量表示末端执行端相对于基坐标的平移向量[19-21]，将所有齐次方程相乘得到各个向量的代数值如下：

（5）

（6）

（7）

（8）

（9）

（10）

式（5）～（10）为拱架抓手组计算结果，由拱架抓手组的正运动学方程计算结果可以看出，该设备的末端执行端的位置只与关节θ1、θ2、...、θ10相关与θ11无关，该为工具坐标系的产物在后续的计算中不用考虑（视为常数值），同理也可以得到凿岩组的计算结果（式子与拱架抓手组相似这里就不做展示），通过其正运动学方程计算结果可以看出在凿岩组的末端执行位置只与θ1、θ2、...、d9相关与θ10无关也将其视为常数值。上面建立的运动学方程，在知道各个关节的具体变化后就能得出末端执行端相对于基坐标系的位置与姿态。

本次工作空间的求解与仿真都在Matlab  平台下进行，本次主要使用了RoboticsToolbox工具箱进行相关的编程与可视化仿真操作[22-23]。鏈式矩阵在Matlab中编写正运动学求解函数 和工具自带正运动学求解函数fkine进行相互验证，结果相同证明其正运动学方程正确。将表1和表2的MOD_DH参数输入并设置关节的运动范围和类型，最后通过SeriaLink函数构建整个模型，在仿真时加入teach函数实现手动控制关节角度的变化来观察模型的运动变化以及位置和姿态的数值变化，得到仿真模型如图3、图4所示。

2 改进遗传粒子群算法逆运动学求解

（1）粒子群算法

受鸟类觅食行为的启发，Kennedy和Eberhart提出了粒子群优化算法（Particle Swarm Optimization，PSO）[15]，但粒子群优化算法在对冗余的机械臂求解的时候会有陷入局部最优的情况，本次选择遗传算法与粒子群相结合并加以改进，本次主要是通过对标准遗传粒子群算法中的初始化以及越界以及权重进行了一定改进，在初始化中引入混沌运动，利用其遍历不重复和伪随机性对种群混沌初始化，在越界上对于超过边界的种群利用标准的粒子群初始化进行重新赋值，这样可以使种群更加多样性避免简单的一刀切而使算法错过最优解，提升搜索能力，利用随机震荡惯性权重在算法刚开始寻优时以高速前进保证搜索速度，在后期减慢速度，提升搜索精度。混沌初始化公式、简单初始化公式分别为：

（11）

（12）

式中： 为粒子的位置；vij为粒子的速度；i和j为第i个粒子的第j维； 、 分别为粒子位置的上下边界； 、 分别为粒子速度的上下边界； 和 是范围为[-1，1]的混沌变量； 、 和 是范围为[0，1]的随机变量。

式（11）和式（12）主要是为增加种群多样性和提升搜索能力。

震荡递减惯性权重为：

（13）

式中：?为震荡递减惯性权重（ 与 一般情况下取0.9与0.4），它可以控制搜索速度； 为最大迭代次数；k为当前迭代次数；e为自然常数，其变化趋势如图5所示。

改进遗传粒子群算法的步骤如图6所示。

（2）目标函数

优化算法求解逆运动学问题是将机械臂逆运动学求解设转化为优化问题，这就需要设置合适的优化目标函数，故本次将使用两个优化目标函数进行逆运动学求解，第一个优化目标函数只考虑末端执行端的位置定义为位置误差

函数，函数设置为 姿态坐标的影响为：

（14）

式中： （i＝x，y，z）为知己的末端执行端的位置； 为智能算法找到的末端执行端的位置，将两者对于相减后得到位置误差。

第二个优化目标函数加入姿态影响，函数设置为：

（15）

式中： 为加权调整系数用于调节位置误差和姿态误差，避免位置误差过大时淹没姿态误差；

而 、 、 、 （i＝x，y，z）为已知矩阵向量； ， ， ， 为智能算法求出关节最后得到

的矩阵向量，对应相减得到误差。

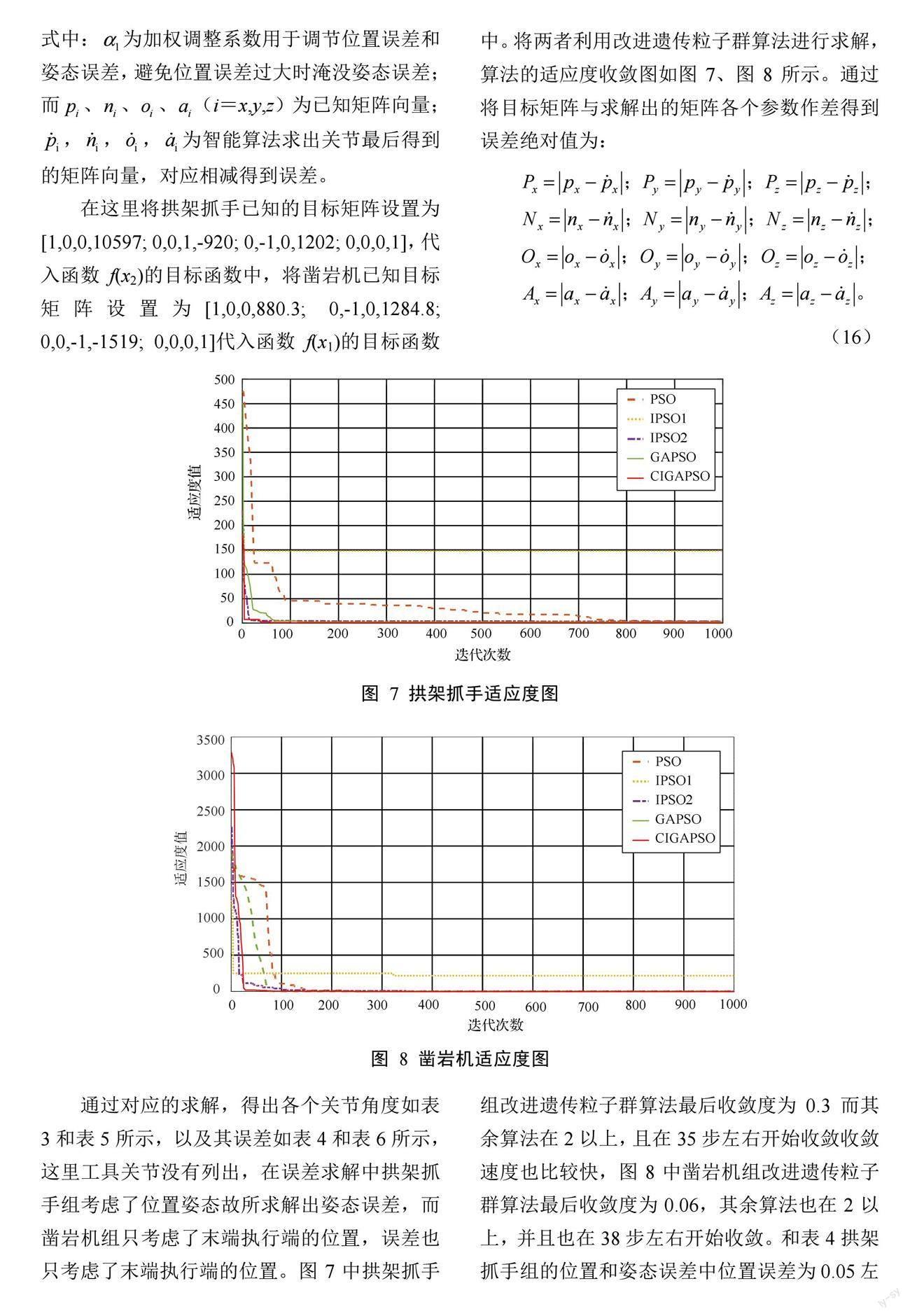
在这里将拱架抓手已知的目标矩阵设置为[1，0，0，10597; 0，0，1，-920; 0，-1，0，1202; 0，0，0，1]，代入函数f（x2）的目标函数中，将凿岩机已知目标矩阵设置为[1，0，0，880.3; 0，-1，0，1284.8; 0，0，-1，-1519; 0，0，0，1]代入函数f（x1）的目标函数中。将两者利用改进遗传粒子群算法进行求解，算法的适应度收敛图如图7、图8所示。通过将目标矩阵与求解出的矩阵各个参数作差得到误差绝对值为：

（16）

通过对应的求解，得出各个关节角度如表3和表5所示，以及其误差如表4和表6所示，这里工具关节没有列出，在误差求解中拱架抓手组考虑了位置姿态故所求解出姿态误差，而凿岩机组只考虑了末端执行端的位置，误差也只考虑了末端执行端的位置。图7中拱架抓手组改进遗传粒子群算法最后收敛度为0.3而其余算法在2以上，且在35步左右开始收敛收敛速度也比较快，图8中凿岩机组改进遗传粒子群算法最后收敛度为0.06，其余算法也在2以上，并且也在38步左右开始收敛。和表4拱架抓手组的位置和姿态误差中位置误差为0.05左右比标准的遗传粒子群算法略高一点，但在姿态误差中为0.08左右均低于其算法，表6中凿岩机的位置误差为0.06左右只别标准遗传粒子高一点。综上可以看出改进遗传粒子群算法在进行逆运动学求解时其收敛速度比较快，在最终求解值的误差也比较小特别是在约束条件多的情况下，该算法可以用于后面类似结构的设备的逆运动学求解上。

3 空间求解

本次的由于分析对象的结构特殊性故分布使用其中一种方法进行工作空间的求解。对于拱架抓手组采用的是基于拉丁超立方体抽样方法进行工作空间求解，对于一个具有N个维度的向量空间，使用M个随机抽样抽取的拉丁超立方抽样步骤第一步为将每个维度的向量进行单独存储，且具有M个分区，保持个区间独立是抽取概率相同，第二步为在每个维度中的每个分区随机抽取一个代表点，第三步为分别将每个维度的向量里面随机抽取第二步骤中的一个点，组成N×M的立方矩阵，最后将所有点代入正运动学程序中求解并将所有点绘制成工作空间云图。

这里的维度设为11，因为拱架抓手组连点工具组可以看做11个关节，对旋转和平移关节进行上下边界的限制如下所示：

（17）

式中： 为旋转关节； 、 分别为最大、最小角度；d为移动关节； 、 分别为最大最小移动距离。

为更加逼近拱架抓手组实际情况这里选择60 000个抽样点这样工作空间求解时的样本点足够多，能够得到更多的空间点绘制出更加接近真实的工作空间云图如图9所示。

接下来采用蒙特卡洛法对凿岩组进行工作空间的求解，蒙特卡洛法步骤更为简单，主要是设置关节上下边界，通过RAND[0-1]的随机函数乘以关节范围，得到各关机的随机变量为：

（18）

移动关节相关处理式子与旋转关节处理式子同理。代入正运动学方程求解将所有点绘制成工作空间云图。

对凿岩机的工作空间求解，这里的维度为10，为更加逼近实际情况，一样选着60 000抽样点，这样工作空间求解时的样本点足够多，能够得到更多的空间点绘制出更加接近真实的工作空间云图如图10所示。

由图9、图10可看出拱架抓手组三维工作空间云图呈现斜向椭球形，通过图中各方向投影图可知拱架抓手组在X轴方向的工作边界为（0 mm： 111 600 mm）、Y轴方向的工作邊界为（-8 200 mm： 5 000 mm）、Z轴方向的工作边界为（-3 100 mm： 11 500 mm），凿岩机组三维工作空间云图同样呈现斜向椭球形，通过图中各方向投影图可得出凿岩机组在X轴方向的工作边界为（-4 800 mm： 15 600 mm）、在Y轴方向上的工作边界为（-11 800 mm： 10 000 mm）、Z轴方向上的工作边界为（-6 900 mm：17 000 mm），这里以双向六车道高速公路中的隧道为参考对象，其属大跨径扁平隧道，其中宽14.5 m、限高5 m，内轮廓净宽为15.25 m、净高7.7 m[24]。可以看出无论是拱架抓手组还是凿岩机组的工作空间边界都能很好的覆盖施工范围，验证了两个工作都能很好的满足施工作业要求。上述得出数据还能发现X、Y和Z轴三个方向上凿岩机组的工作边界基本上完全包裹了拱架抓手的工作边界，这说明在整个工作空间中两个工作组有大量工作空间重叠，若两个工作组若同时工作便可能会发生相互碰撞和干扰且拱架抓手组在工作时其吊篮内会存在工作人员，所以两个工作组不能同时运行以免造成人员危险和设备损坏，如今的主要是通过人为控制和干预，但这还是无法避免一些误操作的情况还需要在控制上还需要加上相关的控制阀防止同时工作或者臂架上的部件加上碰撞检测装置在碰撞后自动后退和停止，避免因为误操作而导致的相关人员危险和设备损失。而其控制难度也比较大，故需求进行轨迹规划来为控制等改进提供理论基础，本文的正运动学和工作空间分析还可为后续的结构改进提供参考。

4 结语

本次以隧道支护设备的一个集成两个功能的机械臂为例进行分析，根据MOD_DH建立正运动学方程，利用改进的遗传粒子群算法通过不同的目标函数进行逆运动学求解，并进行

比较和误差计算，本次改进后的遗传粒子群算法在求解本模型有较好的准确性、效率性和通用性，本更快速的根据本类产品模型的改变进行调整更改，在本类产品的高自由度下能够比较快速和精准的进行求解。通过Matlab Robotics Toolbox对两个功能机械臂进行仿真，利用拉丁超立方和蒙特卡洛法对机械臂空间进行求解与仿真，验证了其满足施工需求，但存在着工作空间的重合，需要设置监控系统避免误操作导致人员和设备的损失，在后续研究中可以针对两个工作系统进行自我避障分析，也为后续的该类似多功能机械臂在控制和结构改进提供理论基础，在工作空间上提供验证参考。

参考文献：

[1]张化平，王宇航，陈汉卿. 六自由度机械臂运动学分析与仿真[J]. 工业仪表与自动化装置，2017（5）：127-130.

[2]李珺茹，齐立群，韩文波. 六自由度机械臂运动学分析与轨迹优化[J]. 长春理工大学学报（自然科学版），2019，42（1）：68-73.

[3]石建平. 基于粒子群优化算法的冗余机械臂运动学逆解[J]. 贵阳学院学报（自然科学版），2020，15（3）：48-52.

[4]冷舒，吴克，居鹤华. 机械臂运动学建模及解算方法综述[J]. 宇航学报，2019，40（11）：1262-1273.

[5]林阳，赵欢，丁汉. 基于多种群遗传算法的一般机器人逆运动学求解[J]. 机械工程学报，2017，53（3）：1-8.

[6]Rokbani N，Alimi A M. Inverse Kinematics Using Particle Swarm Optimization， A Statistical Analysis[J]. Procedia Engineering，2013（64）：1602-1611.

[7]Sancaktar I，Tuna B，Ulutas M. Inverse kinematics application on medical robot using adapted PSO method[J]. Engineering Science and Technology，an International Journal，2018，21（5）：1006-1010.

[8]罗天洪，陈才，李富盈. 基于时变萤火虫群算法的冗余机器人手臂逆解[J]. 计算机集成制造系统，2016，22（2）：576-582.

[9]El-Sherbiny A，Elhosseini M A，Haikal A Y. A new ABC variant for solving inverse kinematics problem in 5 DOF robot arm[J]. Applied Soft Computing，2018（73）：24-38.

[10]Cheng X，Zhao M. The inverse solution algorithm and trajectory error analysis of robotic arm based on MQACA-RBF network[J]. Journal of Robotics，2020（2020）：1-11.

[11]Dereli S，K?ker R. IW-PSO approach to the inverse kinematics problem solution of a 7-DOF serial robot manipulator[J]. Sigma Journal of Engineering and Natural Sciences，2018，36（1）：77-85.

[12]Dereli S，K?ker R. A meta-heuristic proposal for inverse kinematics solution of 7-DOF serial robotic manipulator：quantum behaved particle swarm algorithm[J]. Artificial Intelligence Review，2020（53）：949-964.

[13]石建平. 基于群智能优化算法的冗余机械臂运动学逆解研究[D]. 南昌：南昌大学，2020.

[14]蔡蒂，谢存禧，张铁，等. 基于蒙特卡洛法的喷涂机器人工作空间分析及仿真[J]. 机械设计与制造，2009（3）：161-162.

[15]黄毅. 拱架安装台车工作机构结构设计及仿真优化[D]. 成都：西华大学，2020.

[16]王先伟，吴明晖，周俊，等. 名优茶采摘机器人机械手结构参数优化与仿真[J]. 中国农机化学报，2018，39（7）：84-89.

[17]张鹏. 基于Kriging模型的隧道围岩稳定性分析[D]. 长沙：湖南大学，2009.

[18]Bai Y，Luo M，Pang F. An Algorithm for Solving Robot Inverse Kinematics Based on FOA Optimized BP Neural Network[J]. Applied Sciences，2021，11（15）：7129-7141.

[19]姜宏超，刘士荣，张波涛. 六自由度模块化机械臂的逆运动学分析[J]. 浙江大学学报（工学版），2010，44（7）：1348-1354.

[20]马江. 六自由度机械臂控制系统设计与运动学仿真[D]. 北京：北京工业大学，2009.

[21]Song Q，Li S，Bai Q，et al. Trajectory Planning of Robot Manipulator Based on RBF Neural Network[J]. Entropy（Basel），2021，23（9）：1207-1228.

[22]魏娟. 多自由度機械臂轨迹跟踪控制仿真研究[D]. 湘潭：湘潭大学，2010.

[23]张旭，郑泽龙，齐勇. 6自由度串联机器人D-H模型参数辨识及标定[J]. 机器人，2016，38（3）：360-370.

[24]孟庆誉，李太安. 三车道公路隧道进洞处理及台阶法开挖掘进[J]. 公路，2005（10）：210-214.