广义任务相关成分分析的SSVEP研究
2023-12-11董艳清高程昕
韩 丹,董艳清,高程昕,曹 锐
太原理工大学 软件学院,山西 晋中 030600
脑机接口(brain-computer interface,BCI)系统指在大脑与外部环境之间构建起一条信息传输通道,用户的意图可以通过脑电信号(electroencephalogram,EEG)反映出来,然后通过系统把它转换成所需要的输出形式加以利用[1-2]。BCI 已在医疗、教育、生活以及科研等领域取得了阶段性进展,另一个热点领域是BCI 字符拼写器,其可以帮助患有严重运动障碍(例如肌萎缩侧索硬化症)的患者通过拼写器与大脑进行交流,而无需肌肉活动[3]。因此,BCI 字符拼写器的研究对于患者们正常生活和无障碍交流具有重要意义。
当用户受到固定闪烁频率的视觉刺激时,诱发大脑神经元产生的EEG 频率与所受刺激频率同步,导致相应频率及其谐波的振幅增强,产生稳态视觉诱发电位(steady-state visual evoked potential,SSVEP)[4]。近年来,基于脑电信号的SSVEP 字符识别系统由于信息传输率高(information transfer rate,ITR)、稳定性强和用户操作简单等优势[5],成为近年BCI 研究领域中最热门的应用方向之一。SSVEP-BCI 拼写系统的实现通常是在静态背景下不同位置输出不同的闪烁刺激频率来对应某个指令,如用于脑控打字的字母信息等[6]。
基于SSVEP-BCI的算法可分为无监督方法和有监督方法[7]。无监督方法以即插即用的方式识别刺激频率,如Chen等人[8]提出的典型相关分析(canonical correlation analysis,CCA)及其滤波器组扩展[9]等,以正余弦信号作为参考信号,首次被用于在没有校准的情况下进行SSVEP 检测,然而较高的准确率需要长时间持续刺激,会导致用户视觉疲劳,并且ITR 会有所降低。基于监督的方法通常利用个体的训练数据来构建其模板和空间滤波器,如Nakanishi等人[10]提出的任务相关成分分析(task-related component analysis,TRCA)可以通过最大限度地增强SSVEP-BCI试验之间的可重复性与SSVEP信号的信噪比(signal-to-noise ratio,SNR),从而提高分类性能,是目前SSVEP分类的主要方法之一,然而在短时间窗口(time window,TW)下存在识别率较低的问题[11-12]。而在SSVEP 的在线BCI 应用中,时间窗口的鲁棒性对于SSVEP 中频率识别的具有重要意义。此外,有监督方法多数情况下性能优于无监督方法,但前者的采集数据和训练过程过于繁琐、耗时。例如由于电极位置、环境和患者状态的变化,瘫痪患者在日常生活中使用SSVEP-BCI 时记录EEG 可能无法作为SSVEP 检测算法的验证数据,从而导致BCI系统的低效。如果能够利用用户的校准数据,并与无监督的SSVEP 检测算法相结合,那么分类器就能以较低的训练成本实现高性能。
因此,本研究针对SSVEP-BCI提出了一种广义任务相关成分分析方法(generalized task-related component analysis,GTRCA),充分利用校准数据、测试数据和预定义数据的相关性来提高字符识别准确率和信息传输率。本文使用清华大学脑机接口研究组提供Benchmark 公开数据集来评估算法性能。
1 相关工作
1.1 任务相关成分分析
TRCA[10]是用于提高单独校准的SSVEP-BCI 在不同数据长度下的性能。算法理念是在空间过滤后最大化任务相关组件的可重复性。其基本假设是一个生成模型,其信号模型如下:
其中,x(t)是观察值,s(t)是任务相关分量,n(t)是任务无关分量,a1,j和a2,j是任务相关组件的混合系数,Nch是通道数。s(t)可以通过在空间滤波后最大化试验间协方差来估计,h1和h2是指相同任务下的不同试验:
为了解决优化问题,添加了有限方差的二次约束:
然后,可以从广义瑞利商问题推导出TRCA 空间滤波器:
之后提出的ensemble TRCA 是一种基于TRCA 的集成目标识别方法,它采用了一种集成技术来构成最终的空间滤波器:
其中,m表示方法所采用的滤波器组,Nc表示目标类数。由于有Nc个视觉刺激的单独校准数据,因此可以获得Nc个不同的空间滤波器。理想情况下,它们应该彼此相似,因此可以使用一个集成的空间滤波器进行后续研究。之后研究中滤波器组技术已在文献[10]中得到验证,也可以提高基于TRCA的方法的性能。
1.2 标准典型相关性分析
CCA 是一种探索两组多维变量之间潜在相关性的统计方法。它计算两个多维随机变量A∈Rn×m1和B∈Rn×m2之间的最大相关性,其中n和m1(或m2)是行号和列号。通过优化两个权重向量u∈Rm1×1和v∈Rm2×1来最大化相关性。优化问题可以写成以下方程:
让x=Au和y=Bv,上述等式结果使得皮尔逊相关系数corr(x,y)最大化。集合X和Yf表示多通道EEG信号和SSVEP参考信号。令X=A且Yf=B,上述方程式可以计算脑电信号和参考信号之间的最大相关性。参考信号由下面公式构成:
公式中,fk表示刺激频率,Fs表示采样率,N表示采样点数量,Nh表示SSVEP 信号的谐波数。由于CCA算法受到SSVEP 的非高斯背景噪声和谐波的影响,因此其不能充分利用SSVEP的信息。
1.3 平方相关和
平方相关和SSCOR[13]是对多视图数据的CCA的推广。就像前面提到的TRCA 一样,SSCOR 也是基于个体的训练数据,SSCOR的原始公式是:
其中,所有训练试验组合之间的相关性的二次和在空间滤波器上最大化。在文献[13]中,为了更好地适应SSVEP目标检测任务的要求和特征,作者将其应用为一个新的约束优化问题。表示为所有训练试验的平均值,新的优化问题显示为:
其中,C(0,j)表示均值Γi0与训练试验Γij之间的交叉协方差,C(0,0)和C(j,j)为自协方差矩阵。空间滤波器通过优化单个的SSVEP 模板来学习一个公共的SSVEP 表示空间。SSCOR对SSVEP响应子空间的投影提高了嵌入在记录的EEG 数据中的SSVEP 分量的信噪比以提高性能。
2 数据与方法
2.1 数据集
刺激范式是SSVE-BCI 系统中一个重要的部分。一个良好的刺激范式具有操作简单、性能稳定、产生高质量的SSVEP信号等特点。本文使用清华大学脑机接口研究组提供的Benchmark公开数据集进行研究。
数据集收集了35 名健康被试的SSVEP-BCI 记录,实验时,屏幕上显示了一个5×8的字符矩阵,包含40个以不同频率(8~15.8 Hz,间隔0.2 Hz)闪烁的字符,如图1所示。对每个被试的数据来说,由6 组实验组成,每个实验包含40 个试验,对应于以随机顺序显示的40 个字符。每个实验开始时都有一个视觉提示,该提示在屏幕上出现了0.5 s。受试者被要求在提示时间内尽快将目光转移到目标上。所有的刺激开始在屏幕上同时闪烁,持续5 s。在刺激偏移之后,屏幕在下一次试验开始之前空白0.5 s。收集的脑电图数据被下采样到250 Hz,并根据每个试验分为6 s的数据。数据集的更详细描述在文献[14]中给出。

图1 联合频率和相位调制方法的40个刺激目标Fig.1 40 stimulus targets for combined frequency and phase modulation methods
2.2 数据预处理

图2 电极位置分布Fig.2 Distribution of electrode positions
为了使所提出方法在时间窗口内更有效地学习频率相关信息并且降低肌电、自发脑电等背景噪声的影响,本研究选用六阶零相位Chebyshev I 型无限脉冲响应(IIR)滤波器[16]对数据进行6 Hz 到90 Hz 之间的带通滤波[17]。
由于数据长度对于单独校准的SSVEP-BCI至关重要[18],因此采用的EEG数据样本通过给定不同的时间窗口Nl(范围从0.2 s 到1 s,间隔为0.1 s)来进行选取,如图3所示。本文提取试验刺激开始0.5 s后的数据,并考虑视觉通路引起的140 ms 延迟,选取采样数据范围为[0.64,0.64+Nl]。
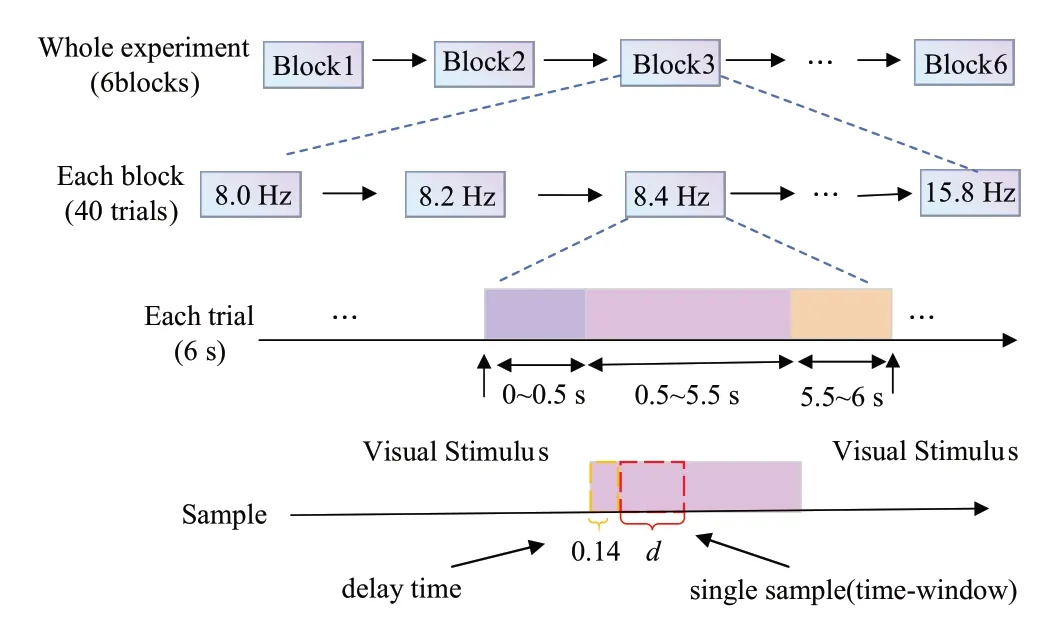
图3 脑电数据选取过程Fig.3 EEG data selection process
2.3 GTRCA
本文提出了一种广义任务相关成分分析的方法来应用于SSVEP-BCI字符拼写系统。方法通过确定一个线性变换,最大化多组变量集合之间的相关性来提高SSVEP-BCI 的分类性能。图4 为GTRCA 的SSVEP 目标识别过程。

图4 GTRCA算法示意图Fig.4 Schematic diagram of GTRCA algorithm
(3)测试信号Xn与参考信号Yn之间的;其中n=1,2,…,Nf,Nf是刺激目标频率的个数。
之后,通过多组相关计算分析得到:一个刺激目标频率n在不同的投影向量之间计算的相关向量,包含了的i个相关系数,i=1,2,3,4,如公式所示:
其中,corr(a,b)表示计算两个向量a和b之间的皮尔逊相关系数。本文通过实验将加权相关系数ρn进一步组合分析作为目标识别的特征:
公式中,选用符号函数sign(·)充分保留来自负相关系数的区别性信息,以便于后续的分析。最后,频率为n的测试样本试验的目标字符T识别公式如下:
从而得到最后字符识别分类结果。GTRCA方法主要通过计算三组数据的不同空间滤波器特征w,即单个模板之间的滤波器、单个模板与参考信号之间以及测试信号与参考信号之间的滤波器,将这些空间滤波器特征结合多通道脑电信号等数据进行的多组相关计算从而得到多组皮尔逊相关系数,之后最大化相关的系数而得到最后字符分类结果。加入的个体模板数据结合了个体特异性特征,从而提高了SSVEP 检测性能。加入参考信号可获得额外信息进而增强模型的鲁棒性并且减少了校准时间,这对于实际的BCI应用至关重要。
2.4 评价指标
本研究使用两个参数来评估SSVEP-BCI 的性能:识别准确率和信息传输率。其中准确率P被定义为正确识别样本数与总识别样本数的比值:
其中,n表示正确样本数,m表示总样本数。ITR 考虑了准确率和时间长度之间的权衡,ITR单位定义为每分钟比特数(bit/min)[19]:
其中,N和T是SSVEP类的数量和选择的平均时间,T包括注视时间和注视移动时间。原始离线实验中的注视移动时间为0.5 s。P是最后的分类精度,同时管理预测精度和信号持续时间之间的权衡,以便实现最大ITR。
在性能评估中,本文选择使用留一交叉验证法,以每个被试者的单个EEG 数据块作测试集,其余数据作训练集,这个过程重复6次。本文计算不同时间窗下的平均准确率和信息传输率指标来评估所提方法的性能。
3 实验结果与讨论
3.1 不同方法的对比实验
为充分评估本文所提出方法在公开数据集Benchmark 的SSVEP 字符识别性能,将GTRCA 与TRCA、SSCOR和CCA方法在不同时间窗下的所有被试的平均准确率和信息传输率进行比较。比较实验中,所选通道、数据等均保持一致。
如图5所示,结果表明GTRCA在平均准确率和ITR方面表现出最佳性能,在所有时间窗口下的性能都优于其余三种方法,图中误差条表示标准误差。GTRCA在时间窗为1 s时平均准确率最高达到了(90.7±4.71)%,在0.8 s时平均信息传输率最高达到了(188.46±18.69)bit/min。在短时间窗0.2 s 时,GTRCA 的平均准确率比TRCA 方法的高5.33%,平均ITR比TRCA方法的高20.1 bit/min。表1 展示四种方法在时间窗口为0.9 s 时的所有被试平均准确率和ITR结果。
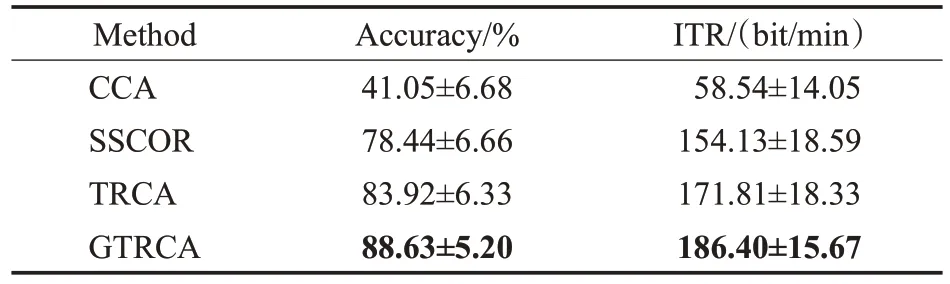
表1 TW为0.9 s时四种方法的被试平均准确率和ITRTable 1 Mean accuracy and ITR of subjects for four methods when TW is 0.9 s

图5 不同时间窗下四种方法的被试平均准确率和ITRFig.5 Average accuracy and ITR of subjects for four methods under different time windows
3.2 训练数据块数的影响
本文对四种方法的分类性能如何随训练数据块数量变化进行了研究。由于只考虑训练数据块数量的影响,实验时需要时间窗口大小保持一致,通过图5 可以观察出时间窗为0.9 s时,准确率和信息传输率结果相对较高,因此时间窗口设定为0.9 s,以便于后续实验观察分析。在有6组数据且使用留一交叉验证的基础上,通过将训练块的数量从5个逐步降低到2个来记录观察四种方法的分类准确率。
结果如图6所示,从图中可以观察到当时间窗口不变时,随着训练块数量的增加,各方法的平均准确率均有不同程度增加,并且也观察到在训练集少的情况下,本文方法依然表现出比其他方法更稳健的性能。
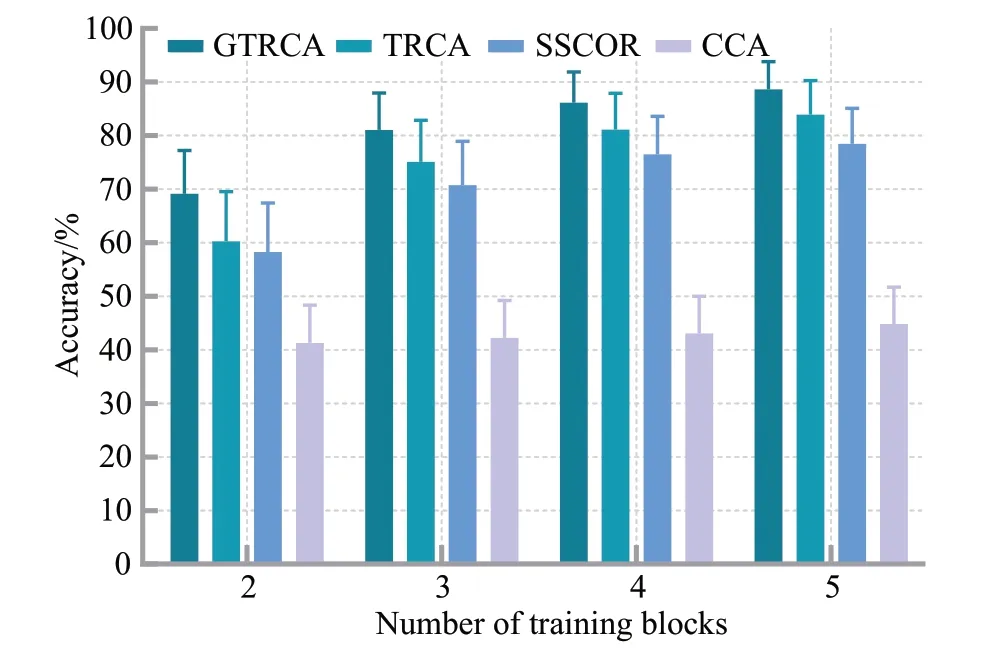
图6 TW为0.9 s时不同训练块数的方法准确率Fig.6 Accuracy of methods with different number of training blocks when TW is 0.9 s
3.3 通道数的影响
为了进一步评估四种方法的分类性能,本文比较了四种方法在不同通道数下的平均分类准确率。除了枕区的九个通道(Pz、PO5、PO3、POz、PO4、PO6、O1、Oz、O2),本文还进行了其他通道数量的实验:包括中央枕部3 通道(Oz、O1 和O2),5 通道(PO5、PO6、Oz、O1 和O2),7通道(PO5、PO3、PO4、PO6、O1、Oz、O2)。
本文将TW同样设置为0.9 s。图7所示为这四种方法在使用不同通道数时的平均分类准确率。结果表明当时间窗口保持不变时,随着通道数量的增加,各方法的平均准确率均有不同程度增加,并且在所有通道数都一样的情况下,所提出的GTRCA 方法都表现出最好的分类效果。

图7 TW为0.9 s时不同通道数的方法准确率Fig.7 Accuracy of methods for different number of channels when TW is 0.9 s
3.4 单因素重复测量方差分析
本文对GTRCA与比较方法中性能较好的TRCA 进行了单因素重复测量方差分析(one-way repeated measures,ANOVA)。当发现显著的主效应(p<0.05)时,使用Bonferroni校正进行F检验的事后比较。统计分析在SPSS Statistics 25(IBM,Armonk,NY,USA)中进行。如表2 所示,单因素重复测量方差分析结果表明,两种方法在所有时间窗的平均准确度存在显著差异。对于ITR,类似地观察到两种方法之间的存在统计学差异。
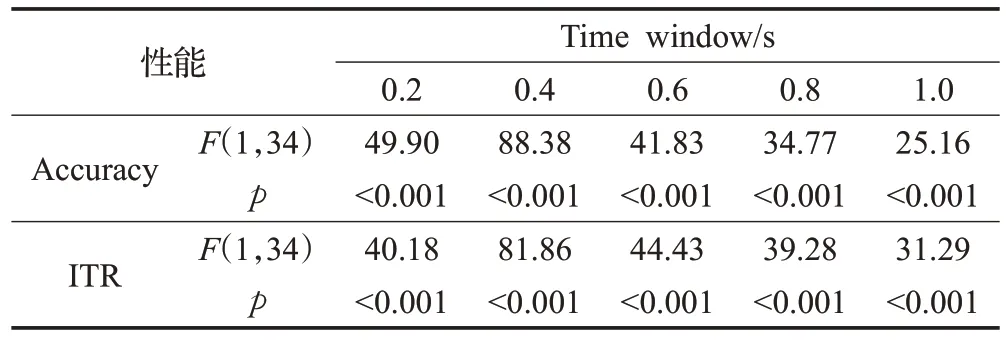
表2 不同时间窗口GTRCA和TRCA 性能的统计分析结果Table 2 Results of statistical analysis of GTRCA and TRCA performance at different time windows
因此,在基准数据集上,GTRCA 方法结果的性能显著优于标准TRCA 方法的性能,证明了GTRCA 在SSVEP频率识别方面的有效性和可行性。
3.5 滤波器组分析
滤波器组分析的目标是将SSVEP数据分解为子带分量,更有效地提取嵌入谐波分量中的独立信息,提高SSVEP的检测。滤波器组分析方法主要包括三个过程:(1)子带分解,(2)每个子带信号的特征提取,以及(3)目标识别。首先,滤波器组分析使用具有不同通带的多个滤波器进行子带分解。本研究的滤波器组选择在[6 Hz~90 Hz]频率范围内,设计覆盖SSVEP 分量上限频率相同的5 个(Nb)谐波频段的子带。如图8所示,该设计有多个具有不同带宽的滤波器来覆盖所有SSVEP数据及其谐波。
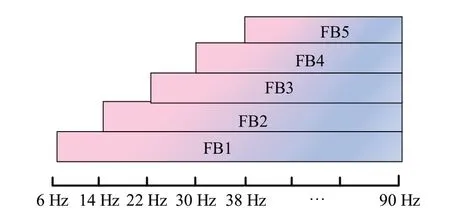
图8 滤波器组设计策略Fig.8 Filter bank design strategy
经过滤波器组分析后,采用特征提取方法应分别用于每个子带分量。计算所有子带分量对应的相关值的加权平方和作为目标识别的特征:
其中,m为子频带的索引。在公式中为所计算的两组数据之间的最大相关系数,子带分量的权值定义如下:
其中,a和b是使分类性能最大化的常数。本文将a和b的值分别设为1.25和0.25。
本文检验了四种方法在不同时间窗的滤波器组方法的性能,如图9 所示,图中误差条表示标准误差。从图中观察到每种方法采用滤波器技术后,字符识别平均准确率、ITR与图5原有方法的相对比有所提高,并且本文所提出的方法仍优于其他四种方法,表明本文方法在SSVEP字符识别分类具有良好稳定的性能。
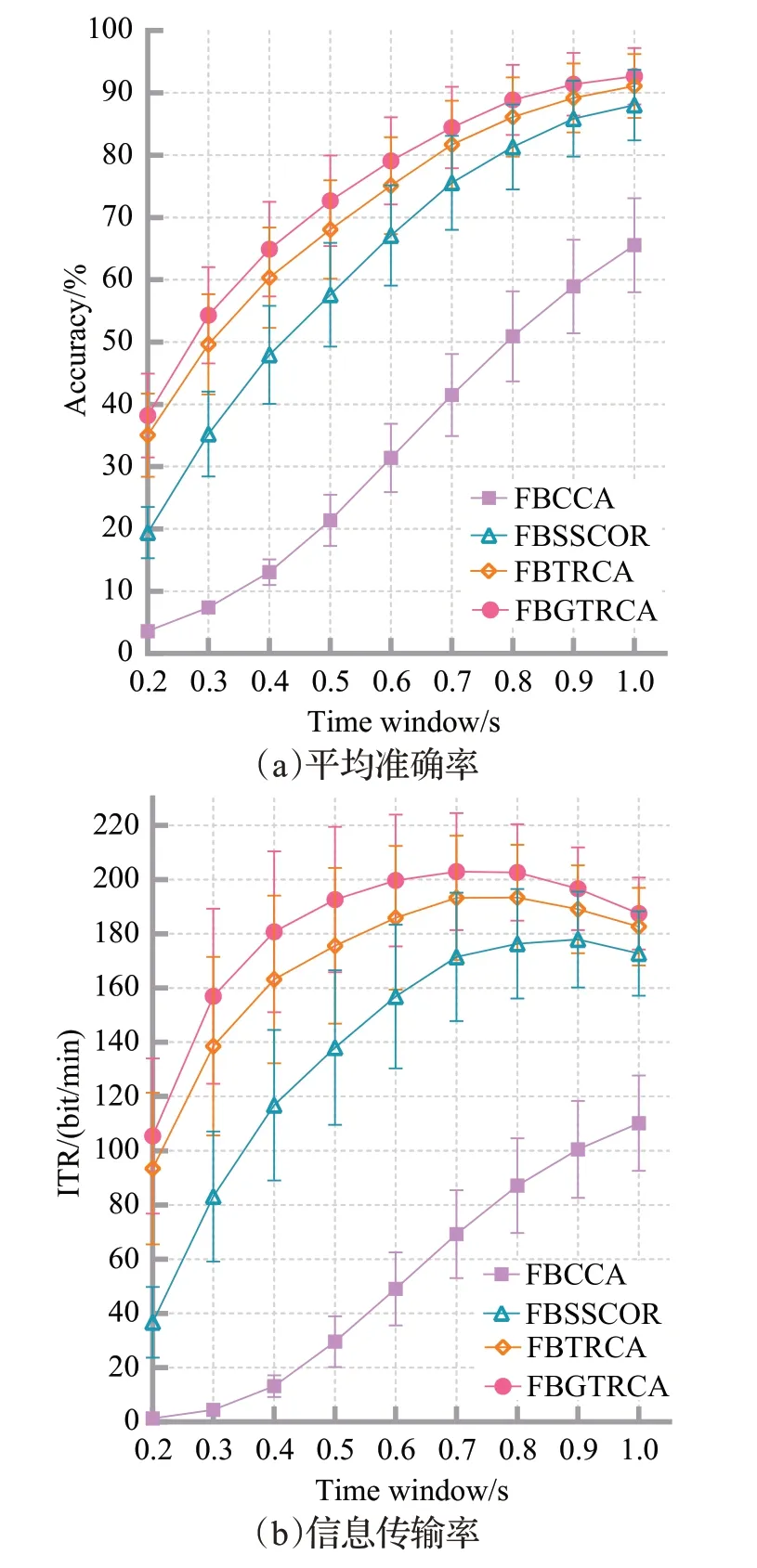
图9 不同时间窗的滤波器组方法平均准确率和ITRFig.9 Accuracy and ITR of filter bank methods with different time windows
4 结束语
本文提出了一种GTRCA 方法,最大化单个训练数据、测试数据、预定义的正弦余弦信号三组数据之间的相关性,充分利用训练数据和预定义的正弦余弦信号的先验知识获得空间滤波器以提高SSVEP 的识别性能。在Benchmark数据集上进行了实验,结果表明所提出的GTRCA方法识别准确率和信息传输率明显优于所比较的方法,尤其是在考虑到有限的训练数据时,即在采用更短时间窗口、更少电极或更少训练块的情况,此外,滤波器技术也适用于GTRCA,FBGTRCA 算法性能较GTRCA有明显提高。
本文只考虑了基于GTRCA的方法中的线性变换以及最大相关系数对应的权重向量,然而脑电信号是非线性和非平稳的,在未来将探索GTRCA 非线性和更多有效的权重向量,这可能会进一步提高分类性能,使更多基于SSVEP-BCI的潜在应用成为现实。
