自适应多密度峰值子簇融合聚类算法

陈 迪，杜 韬，2，周 劲，2，仵匀政，王心耕

1.济南大学 信息科学与工程学院，济南 250024

2.山东省网络环境智能计算技术重点实验室，济南 250024

聚类作为一种无监督的学习方法，只需基于数据本身特征计算出数据对象间的相似度即可实现数据集的划分[1]。通过聚类处理后，同一簇内的数据应尽可能相似，不同簇间的数据应尽可能相异。目前，聚类算法的研究方向包括基于划分的聚类[2-3]、基于密度的聚类[4-5]、基于网格的聚类[6-7]、基于模型的聚类[8-9]、深度聚类等[10-11]。K-Means是一种经典的基于划分的聚类算法，首先随机选取K个点作为初始聚类中心，计算其余点到各中心的距离，进而将其划分给离它最近的中心所属簇中，之后基于目标函数调整聚类中心的位置以及非中心点的分配结果，直到目标函数最小[12]。这种基于划分的聚类算法采用欧式距离最近的划分原则，因此对非球形簇的聚类效果较差。基于密度的聚类方法可以处理任意形状的簇。DBSCAN 算法是最具代表性的一种基于密度的聚类算法，该算法将样本空间划分为高密度区域与低密度区域，将密度相连点的最大集合看作簇[13]。在密度聚类的基础上，Rodriguez和Laio[14]于2014年提出了一种基于密度峰值的聚类算法DPC（density peak cluster），该算法使用局部密度和上级点（局部密度大于它的最近点）距离作为描述数据的两个特征，构建决策图来快速选取聚类中心。虽然该算法可以快速选取聚类中心点，且非中心点的分配只需进行一次，但是DPC 算法仍存在缺陷，具体表现在以下几个方面：（1）DPC算法在计算局部密度时所使用的方法对参数敏感；（2）在DPC算法的分配阶段，易出现连锁效应，即当局部密度较大的样本出现分配错误时，会导致隶属于它的样本发生同样的分配错误；（3）DPC 及其部分改进算法采用手动选取聚类中心点的方式会导致密度稀疏簇的中心点被忽略，从而影响最终的聚类结果。

为改进局部密度的计算方式，一些学者将K近邻（KNN）思想引入DPC 中。Du 等人[15]提出了DPC-KNN算法，将局部密度的计算空间缩小至样本的KNN 邻域中，不仅减少了计算成本，而且更加精确地描述了样本的局部密度。Jiang等人[16]同样使用KNN的思想对上级点距离的计算方式进行改进，使中心点和非中心点之间的差异变大，进而方便中心点的选取。然而，这些引入KNN 对DPC 进行改进的算法，其聚类效果仍受K值大小的影响，当K值过小时，原本存在的邻域关系会被忽略，导致具有相同特征的样本被错误地划分为不同簇中。当K值过大时，具有不同特征的样本会被错误地分类到同一簇中[17]。为尽量避免连锁效应产生，Xie 等人[18]提出了FKNN-DPC算法，使用两种策略对非中心点进行分配。第一种策略是从聚类中心点开始进行最近邻广度优先搜索来进行分配，第二种策略利用近邻加权方法分配离群点和尚未分配的数据点。Abdulrahman等人[19]提出了一种基于密度主干的改进算法DPC-DBFN。该方法利用模糊邻域核来提高聚类的可分性，使用基于密度的KNN 图来标记主干。在分配时首先分配主干，其次利用KNN方法将边界点分配给相对应的密度主干区域。Liu等人[20]提出一种基于共享邻居的密度峰值聚类算法SNN-DPC。该算法使用共享邻居关系对局部密度与上级点距离进行重新定义，并提出了两步分配的方法使算法更具鲁棒性。上述方法都在一定程度上缓解了连锁效应对聚类结果产生的影响。为实现聚类中心点的自动选取，Chen等人[21]提出了一种域自适应密度聚类算法DADC。该算法分别为局部密度和上级点距离设置阈值，规定大于阈值的点为聚类中心点，该算法还提出了一种聚类融合度模型，通过评估相邻集群之间的融合度，实现碎片簇的合并。赵力衡等人[22]提出一种去中心化加权簇归并的密度峰值聚类算法，通过划分高密度区域选取核心样本组，以此取代手动选取聚类中心的方式，最后使用近邻思想分配剩余样本点。

目前团队已解决DPC算法对参数敏感以及分配过程易出现连锁效应的缺陷。通过引入自然邻居思想，不断扩展邻域范围，自适应得到每个点的邻域关系，之后基于自然邻居计算样本的局部密度与上级点距离，避免了人工设定参数对聚类结果的影响。同时，在分配阶段，提出一种两阶段分配策略，首先分配聚类中心附近的密集点形成聚类雏形，再使用隶属上级点的方式分配剩余点[23]。本文在此基础上，进一步提出了一种自适应多密度峰值子簇融合聚类（adaptive multi-density peak subcluster fusion clustering，AMDFC）算法。为防止稀疏簇的中心点被忽略，算法提出一种自动选择策略确定子簇中心。同时，为实现子簇的融合，提出一种K近邻相似度度量准则，合并相似度高的子簇得到最终的聚类结果，使算法更加适合处理密度不均匀的数据集。为验证该算法的有效性，实验部分使用聚类精度（ACC）、标准化互信息（NMI）和调整兰德指数（ARI）三项聚类评价指标对不同聚类算法在二维合成数据集和UCI 真实数据集得到的聚类结果进行对比分析。实验结果表明，AMDFC算法聚类性能优于对比算法。

1 相关工作

1.1 密度峰值聚类算法

密度峰值聚类算法基于两个前提：（1）聚类中心点的局部密度大于其周围点的局部密度。（2）不同中心点之间的距离相对较远。DPC 使用局部密度和上级点距离对数据点进行详细描述。对于局部密度，DPC使用截断距离或高斯核函数方法来计算。

其中，n表示数据规模，dij表示数据点i和j之间的欧氏距离，dc为截断距离参数。上级点距离指的是该点到局部密度大于它且离它最近点的距离，其计算公式如下：

在获取所有数据点的局部密度和上级点距离值后，为快速识别中心点，DPC以ρ为X轴，δ为Y轴绘制决策图进行中心点的选取，中心点即ρ和δ值大的点。同时，DPC 还提出γ-决策图的概念。γ值是局部密度与上级点距离的乘积，值越大，该点作为聚类中心点的概率越大。

在挑选出中心点之后，为这些中心点分配不同的标签，对于非中心点，将其分配给上级点所归属的簇中，若上级点尚无所属的簇，则迭代寻找其上级点完成分配，得到最终的聚类结果。

1.2 自然邻居

自然邻居是一种自适应邻居概念，可以有效解决邻居关系中邻域大小选择的问题[24]。下面对自然邻居的相关概念进行介绍。

定义1（K最近邻）设数据集为X，待处理的数据点为a，则a的K最近邻为一组对象b，定义如下：

定义2（反向K最近邻）点a的反向K近邻为一组对象b，这些对象将a作为它们的K近邻，定义如下：

定义3（自然邻居）对于点a，若它的自然邻居为b，则满足a和b互为邻居，定义如下：

定义4（稳定状态与自然特征值）自然邻居的获取是一个逐渐扩大搜索范围的过程，直到除噪声点之外，所有数据点至少有一个自然邻居时终止，此时认为该数据集达到稳定状态，此时K的取值称为自然特征值，用λ表示。

自然邻居的获取过程是：首先找到样本空间中每个数据点的K近邻，根据反向K近邻关系确定互邻居关系，之后不断扩大K值，直到除噪声点外，所有点都至少有一个自然邻居时终止。

算法1自然邻居搜寻算法

输入：数据集X。

输出：自然特征值λ，各点的自然邻居。

步骤1初始化K=1，为数据集X创建KD 树，为每个样本点构造近邻集合；

步骤2使用KD树搜索样本的第K近邻，并加入到该样本的近邻集合；

步骤3利用反向邻居关系判断两样本点是否互为邻居，若是则二者建立自然邻居关系；

步骤4扩大K值，重复步骤2与步骤3，直到所有样本都至少有一个自然邻居时停止；

步骤5获取所有样本点的自然邻居，以及全局自然特征值λ。

2 AMDFC算法

AMDFC算法依据流程可分为四部分：（1）基于自然邻居计算点的局部密度等度量值；（2）基于自动选取策略选取聚类中心点；（3）基于两阶段分配策略实现非中心点的分配；（4）基于K近邻相似度实现子簇融合。下面对这四部分内容进行详细介绍。表1 为本文所定义的数据符号及其含义。

表1 符号及表示含义Table 1 Symbols and their meanings

2.1 自适应计算数据点的局部密度等度量值

原始DPC 算法在计算局部密度时，只考虑数据的全局结构而缺少局部分析，因此在处理非均匀密度簇的数据集时表现不佳。如图1所示，该数据集由三个不同密度分布的心形簇组成。使用DPC算法对该数据集进行处理，当截断距离取2 时，左上和下方两个簇被划分为同一个聚类。当截断距离取20 时，右上和下方的两个簇被划分为同一个聚类。在该数据集上，DPC无法选取合适的参数来准确完成聚类任务。除此之外，DPC算法在计算局部密度时需全体样本参与，因此当数据规模过大或维度过高时，计算成本大。考虑样本点的邻域信息不仅可以缩小局部密度的计算空间，在一定程度上减小计算成本，同时让算法更适合处理多密度簇数据集。

图1 DPC算法在多密度数据集上的聚类结果Fig.1 Clustering results of DPC on dataset with different density

为考虑样本邻域信息且解决参数敏感问题，本文借助自然邻居思想自适应获取数据点的邻域信息，进而计算局部密度等相关度量值。首先自适应获得样本自然邻居，之后计算样本的局部密度，为使算法适应更多的数据分布情况，本文使用三种核函数分别计算样本局部密度。

上述公式均满足样本的邻居越多且距离该点越近，该点的局部密度越大。在实验环节，针对不同的数据集分别使用三种方法进行计算，并以聚类精度为准，从中选出最优的方法来处理该数据集。

为使聚类中心点的局部密度更加突出，对Chen 等人[21]提出的域密度定义进行改进，将局部密度更新为局部域密度。

定义5（局部域密度）数据点i的局部域密度等于点i的局部密度和其自然邻居局部密度的加权和。

其中，权重系数ω为自然邻居到该样本距离的倒数，距离越近，自然邻居的权重越高，反之，权重越低。由于聚类中心点的自然邻居数目多于非中心点，因此使用局部域密度代替局部密度可以使聚类中心点更加突出。

对于每个样本点，计算其上级点距离：

得到每个数据点的局部域密度DD和上级点距离δ后，将二者相乘得到γ值，点的γ值越高，被选取为聚类中心的概率越大。

通过引入自然邻居思想，算法无需设定K值即可自适应获取样本邻域信息，进而计算样本的局部密度等度量值，解决了参数敏感问题。

2.2 聚类中心自动选取策略

原始DPC 算法分别以局部密度ρ和上级点距离δ作为X轴和Y轴构建决策图，并且人工选取决策图右上角的点，即局部密度与上级点距离大的点作为中心点。除此之外，还可以选取γ值大的数据作为聚类中心。这种方式可以快速发现大部分数据集的聚类中心。然而在一些密度不均匀的数据集中，密度较为稀疏簇的聚类中心极易被忽视，这时通过人工选取的聚类中心点可能无法反映真实聚类中心点的分布情况。下面以Jain数据集为例进行说明。

Jain数据集由两个簇组成，其中上半部分的簇相较下半部分的簇分布更为稀疏，导致该簇中心点的局部密度较小，从而在手动选取中心点时，该簇的中心点容易被忽略。由图2（c）得，选出的两个聚类中心点都分布下半部分的簇中，上半部分簇的中心点并没有被选取。由图2（f）可得，即使DPC 选取3 个聚类中心点，仍没有选取到上半部分簇的点，这导致了较差的聚类结果。由此可见，人工选取聚类中心点的方式由于受先验知识的影响，在中心点的选取数量上一般接近真实簇的数量。但在一些密度分布不均匀的数据集上，一些密度较稀疏的簇中心因其γ值相对较小，容易被忽略。针对这一问题，提出一种聚类中心点自动选取策略，设定一个参数c，在得到所有样本点的γ值后，选取γ值前c%的点作为聚类中心点。该策略的意义在于保证密度稀疏簇的中心点尽可能被选取。以Jain数据集为例，图3 为该数据集的γ决策图，图中分别标注了降序排列后第1%，第2%，第3%，第4%和第5%的点，可以看到，γ值排在5%后的点分布平稳，这些点成为中心的概率极低。经大量实验后确定当c的取值范围在1%～5%之间时，大部分数据集的所有簇中心点都能被选取。下面对局部密度等度量值的计算以及聚类中心的选取流程进行介绍：

图2 手工选取聚类中心在Jain数据集上的聚类结果Fig.2 Clustering results of manually selected cluster centers on Jain dataset

图3 Jain数据集γ 决策图Fig.3 Jain dataset γ Decision graph

算法2度量值计算及中心点选取

输入：数据集X，聚类中心点比例参数c，自然邻居。

输出：局部域密度DD、上级点距离δ、γ值，中心点。

步骤1计算样本点之间的欧氏距离；

步骤2根据式（8）或式（9）或式（10）计算样本点局部密度ρ；

步骤3根据式（11）计算样本局部域密度DD；

步骤4根据式（12）计算样本上级点距离δ；

步骤5根据式（13）计算样本局部域密度与上级点距离乘积γ；

步骤6选取γ值前c%的数据点作为初始聚类中心点。

2.3 两阶段分配策略

在得到聚类中心点后，需要完成非中心点的分配任务。原始DPC算法需要通过迭代查找上级点的方式确定非中心点的归属，此时若一个密度较大的上级点出现分配错误，则隶属于它的点也会产生同样的分配错误，这种现象称为连锁效应。为了降低连锁效应出现的概率，需要尽量减少上级点的迭代查找次数。本文提出一种两阶段的分配策略。提出了稠密点的概念，稠密点指围绕在中心点周围且自然邻居较多的点。在分配时首先将中心点的标签分配给稠密点得到聚类雏形，聚类雏形的生成意味着非中心点的分配无需多次迭代即可找到对应的上级点，之后再使用寻找上级点的方式完成第二步分配，得到聚类结果。

定义6（稠密点）自然邻居数大于等于自然特征值一定比率的点为稠密点。

第一步分配策略采用扩散的方式，首先将中心点的标签扩散给它自然邻居中的稠密点，之后若稠密点的自然邻居也为稠密点，则将标签进一步扩散。不断重复此过程直到所有的稠密点都分配完毕后停止。经过第一步分配，各簇形成聚类雏形。第二步采用隶属于上级点所在簇的方法完成剩余数据点的分配任务，由于聚类雏形已经形成，上级点不需多次迭代即可找到，从而降低连锁效应出现的概率。下面给出两步分配策略流程：

算法3两步分配策略

输入：比率参数α。

输出：聚类结果。

步骤1将所有样本点置于未分配状态；创建一个稠密点队列Dense，所有聚类中心入队；

步骤2从稠密点队列中取一个点，对其自然邻居进行判断，若满足稠密点条件且处于未分配状态，则将中心点标签扩散给它并将它加入队列；

步骤3重复步骤2，直到所有稠密点分配完毕；

步骤4针对未分配数据点，使用隶属于上级点的方式完成第二步分配；

步骤5得到聚类结果。

图4 以Aggregation 数据集为例展示了两阶段分配过程。Aggregation 数据集包含了七个凸状簇。图4（a）为数据集分布情况。首先找到数据集中的稠密点，将聚类中心点的标签扩散式分配给其稠密点。图4（b）为经第一步分配后得到的结果，可以看到此时每个簇的雏形已经生成。第二步分配采用隶属上级点所在簇的方法分配剩余点，图4（c）为两阶段分配得到的最终聚类结果。经过两次分配之后数据被成功划分为七个簇，证明该方法提升了分配效果，并且由于减少了上级点迭代查询次数，因此在一定程度上减少了运行成本。

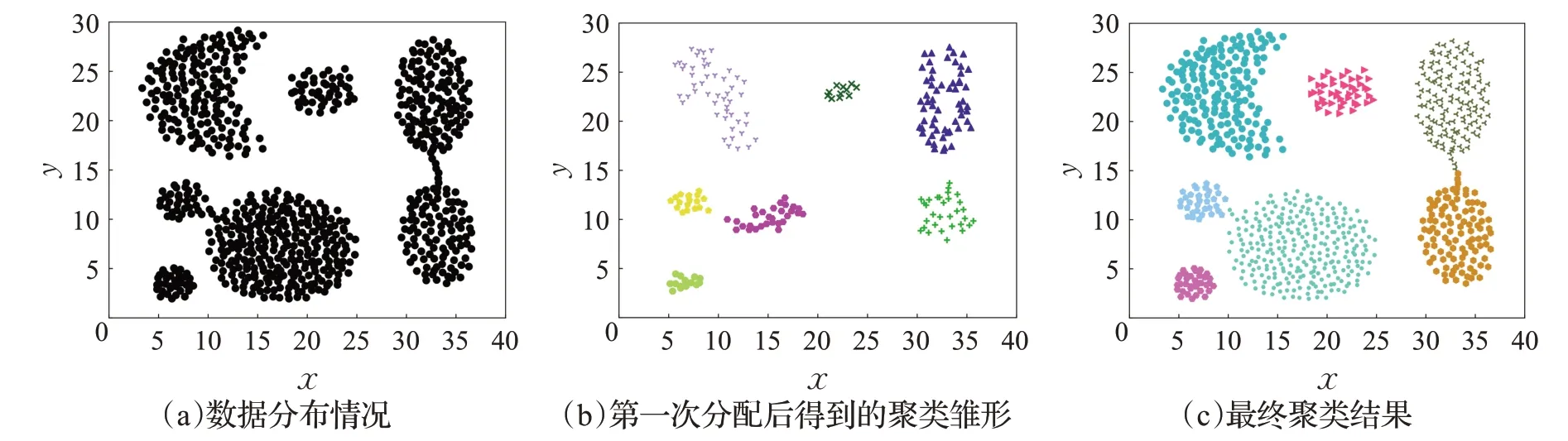
图4 两阶段分配策略在Aggregation数据集上的聚类过程Fig.4 Clustering process of two-stage allocation strategy on Aggregation dataset

2.4 基于K近邻相似度的子簇融合策略

通过上述分配步骤已得到初步聚类结果。此时，若c值较大，则生成簇的数量大于真实簇的数量，需要对子簇进行融合。子簇融合的依据是子簇之间的相似度，目前簇间相似度一般通过簇间平均距离、最大距离、最小距离等方法进行衡量，然而这类方法易受噪声点的影响。针对该问题，提出一种K近邻相似度的度量指标来测量子簇之间相似度。这里的K值一般设定为数据集的自然特征值λ。通过计算簇之间点的K近邻相似度得出子簇之间的相似度，若子簇间的相似度大于规定阈值st（similarity threshold），则将两子簇融合。之后不断迭代直到没有两子簇的K近邻相似度高于阈值时停止，得到最终的聚类结果。

定义7（K近邻相似度）对于簇A中的点i，若i的K近邻有一部分落在簇A中，另一部分落在簇B中，则证明簇A与簇B是相邻的，这种点越多，证明两个子簇越相似。

上述公式中，s(i,A→B)∈[0,1]，其中|KNN(i,A)|表示点i的K近邻落入簇A的数量，|KNN(i,B)|表示点i的K近邻落入簇B的数量，二者越接近，公式的值越接近1，二者相差越大，值越接近0。簇A和簇B的K近邻相似度由下面公式计算，由于K近邻相似度不具有对称性，因此簇A和簇B的相似度等于簇A和簇B中所有点的K近邻相似度之和，值越大表示两子簇越相似。：

在计算出两两子簇的K近邻相似度后，选出最相似的两子簇，若其相似度大于规定阈值，则将两簇融合得到全新的簇。之后不断进行迭代融合，直到最大的子簇相似度小于阈值时停止。下面给出子簇融合流程。

算法4基于K近邻相似度的子簇融合策略

输入：融合阈值st。

输出：聚类结果。

步骤1根据式（15）与式（16）计算两两子簇的K近邻相似度，选出其中的最大值Smax；

步骤2判断Smax是否大于融合阈值st，若满足条件，则将子簇融合；

步骤3重复步骤1 和步骤2，直到没有满足融合条件的两子簇；

步骤4得到聚类结果。

下面以Jain 数据集为例展示子簇融合过程。实验设定c=4，即取γ值前4%的点作为聚类中心点进行分配，得到的初步聚类结果如图5（a）。可以看到经过两步分配策略，共生成12 个初始子簇。之后计算子簇间的K近邻相似度并进行子簇融合，得到最终的两个簇。图5（b）～（h）为选取的部分融合过程，图5（i）表示最终的聚类结果，可以看到，该方法实现了对Jain 数据集的准确划分。

图5 Jain数据集子簇融合过程Fig.5 Sub cluster fusion process of Jain dataset

下面对算法各环节的时间复杂度进行分析。假设数据集中数据对象个数为n，使用KD树搜索样本近邻所消耗的时间为O()nlbn，因此自然邻居搜索的时间复杂度为O()nlbn。借助自然邻居计算局部密度等度量值的时间复杂度为O(n2)，分配阶段需遍历所有数据点，因此时间复杂度为O(n2)。在子簇融合阶段，需计算每个子簇与其余子簇间的相似度。假设初始聚类数为m，该环节的时间复杂度为O()。综上，算法整体时间复杂度为O(n2)。

3 实验结果与分析

实验部分使用7个二维合成数据集与4个UCI真实数据集测试算法性能，其中二维合成数据集包括不同形状与不同规模的数据，表2 和表3 对这些数据集进行介绍。聚类结果使用聚类精度（ACC），标准化互信息（NMI）以及调整兰德系数（ARI）3 个指标进行对比，ACC 与NMI 指标的取值范围为[0，1]，ARI 指标的取值范围为[-1，1]。值越接近1表示算法性能越好。对比算法包括K-Means、DBSCAN、DPC[14]以及近年来对DPC进行改进的算法（FKNN-DPC[16]、SNN-DPC[20]、DBFN[19]、FSDPC[25]），还包括一种深度嵌入式聚类算法IDEC[26]。在参数设置环节，本文提出的算法需要设定聚类中心比例参数c，稠密系数a以及簇融合阈值st。对比算法中，K-Means算法需设定聚类个数，DBSCAN算法需设定邻域半径以及最小数据点数，DPC 与FSDPC 算法需给定聚类中心数量以及截断距离，FKNN-DPC 与SNN-DPC算法需要给定聚类中心数量以及邻域大小，DBFN算法需给定聚类中心数量、邻域大小以及边界点阈值。对于IDEC 算法的训练过程，采用小批量样本进行随机梯度下降和反向传播，KL 散度聚类系数设置为1，学习率设置为0.001。

表2 二维合成数据集详细信息Table 2 2D synthetic dataset details

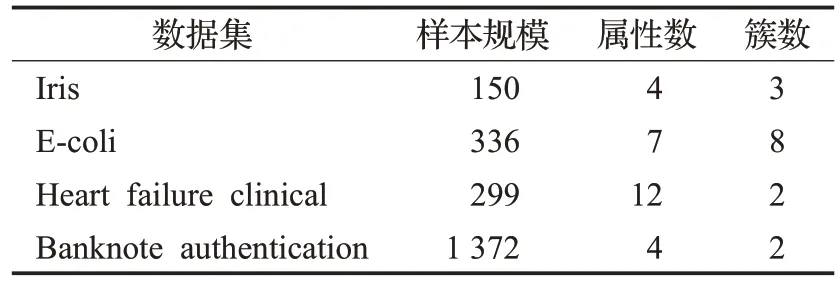
表3 UCI数据集详细信息Table 3 UCI dataset details

3.1 二维合成数据集实验结果

本节选取7个二维合成数据集用于算法性能测试，这些数据集由多个任意形状与非均匀密度簇组成。表4为AMDFC 与对比算法的聚类评价指标对比。其中KMeans算法适合处理球形簇，R15数据集由15个球形簇构成，因此K-Means 算法在该数据集上表现最优，在其余含有非球形簇数据集上的聚类效果较差。DBSCAN算法能够识别任意形状的簇，但是该算法需设定全局参数，因此不适合处理变密度数据集，在3circles、Smile、Twomoons、R15 这些密度均匀的数据集上DBSCAN 聚类效果较好，但在Jain等密度不均匀的数据集上效果较差。原始DPC 算法忽视了邻域信息，且手工选取中心点的方式容易忽略密度稀疏簇的中心，因此在Jain、3circles、Smile、Twomoons 等数据集上效果并不理想。FKNN-DPC、DBFN、SNN-DPC以及FSDPC算法虽然考虑样本的邻域信息，聚类效果相比DPC算法有所提升，但这些算法没有实现簇中心自动选取，处理多密度数据集的能力较差。IDEC算法除在R15数据集上性能最优之外，在其余数据集上表现均没有达到最优，这是因为神经网络聚类算法常用于处理高维文本及图片数据集，数据集的维度越大，相应的优化参数就越多，神经网络的拟合能力就会越强，因此在低维空间中神经网络聚类的性能较差。AMDFC 算法很好地实现了任意形状及密度数据集的聚类任务，由表可得，该算法在Jain、3circles、Smile、Twomoon数据集上聚类精度等指标均达到1，在Aggregation 与Pathbased 数据集上，算法同样表现出最优性能。在R15数据集上虽未表现出最优性能，但是与最优算法的精度差距不大。图6～图9 分别展示了不同算法在Jain、3cirles、Smile 以及Twomoons 数据集上的聚类结果。其中（a）～（h）分别表示K-Means、DBSCAN、DPC、FKNN-DPC、SNN-DPC、DBFN、FSDPC以及AMDFC 算法的聚类结果。为避免样本顺序对IDEC 聚类结果产生影响，在每一轮训练时均打乱原始数据顺序，随机打乱后的样本更接近真实分布。若不打乱样本顺序，使用排序的样本进行训练会使神经网络学习样本顺序，从而影响泛化能力。每轮打乱后的顺序是未知的，无法使样本与标签对齐，有关IDEC的聚类结果在表格中以数据形式进行展示。

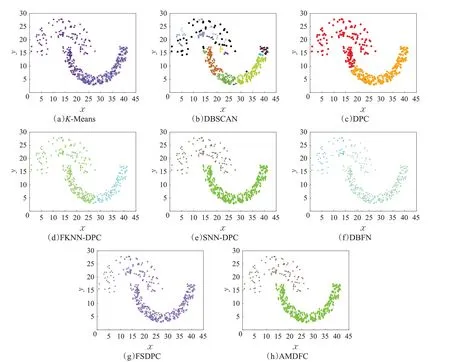
图6 Jain数据集聚类结果Fig.6 Clustering results of Jain dataset

图7 3circles数据集聚类结果Fig.7 Clustering results of 3circles dataset

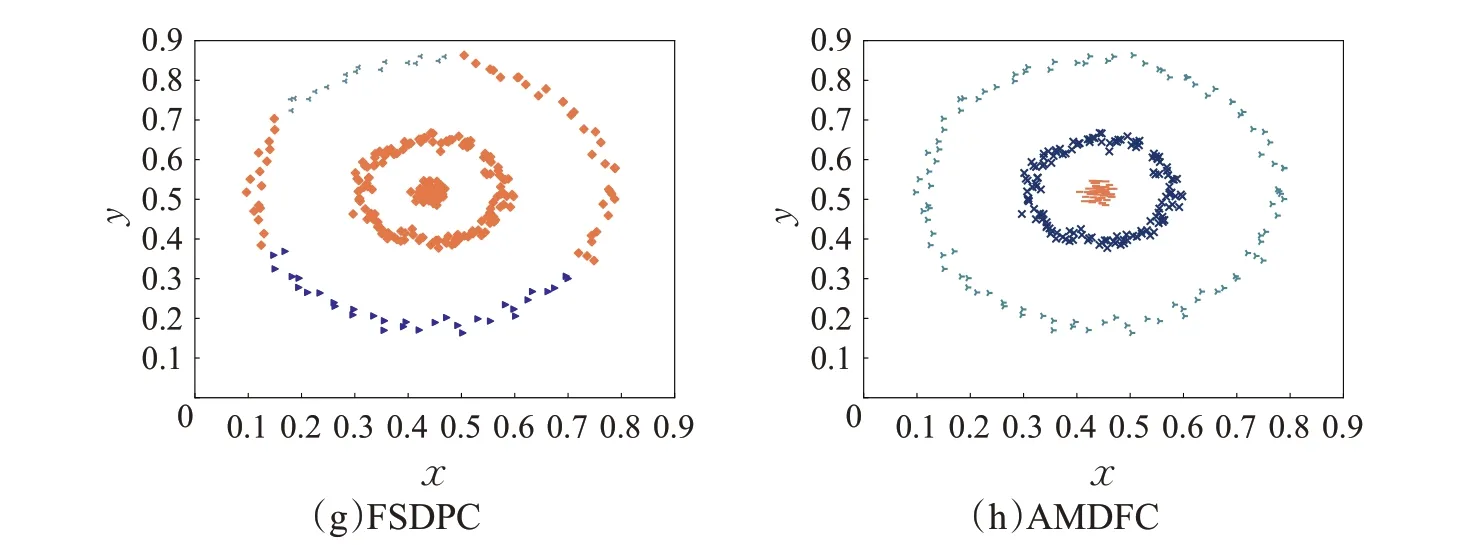
图7 （续）

图9 Twomoons数据集聚类结果Fig.9 Clustering results of Twomoons dataset

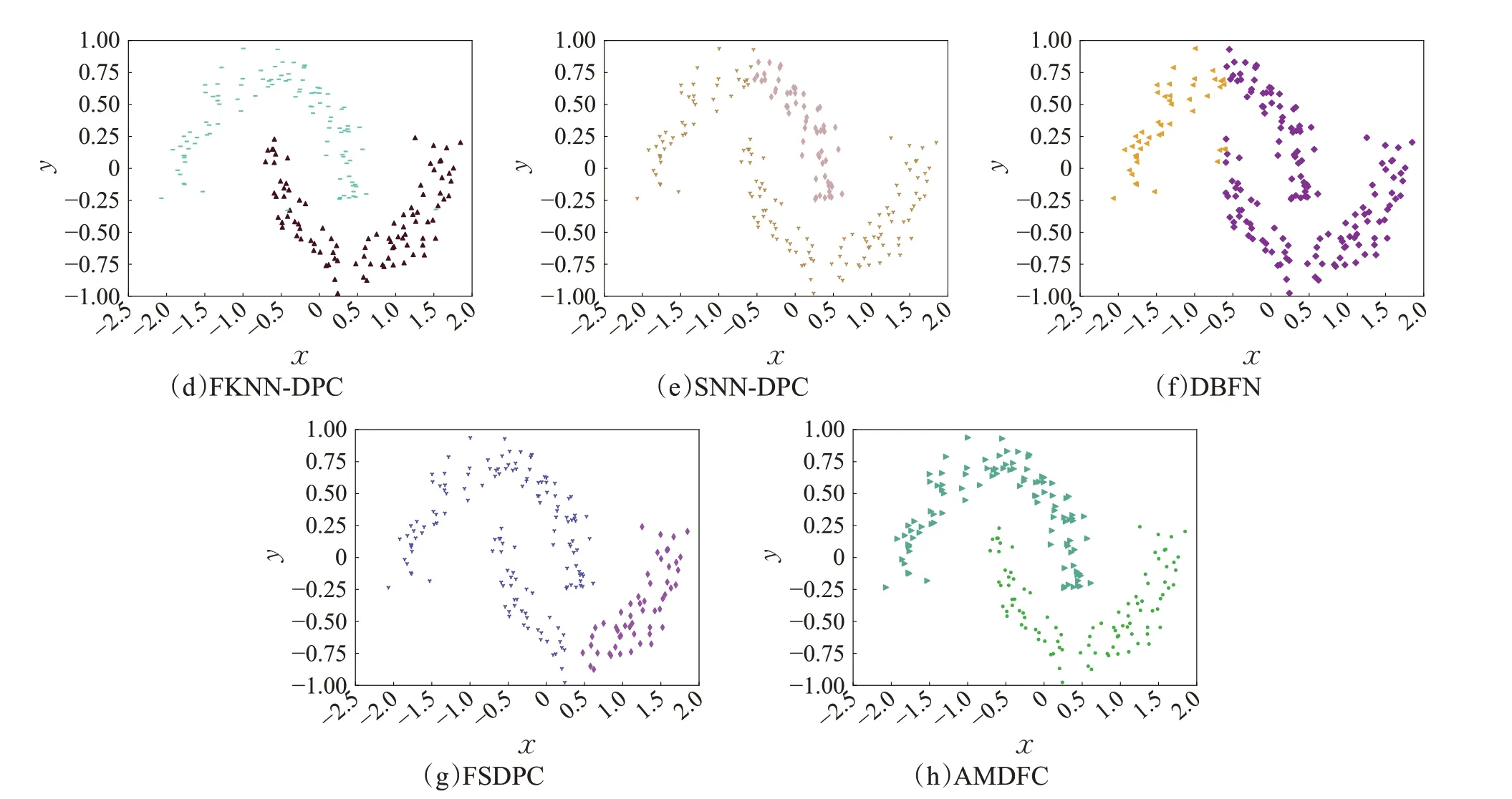
图9 （续）

表4 各聚类算法在合成数据集上的评价指标对比Table 4 Comparison of evaluation indicators of various clustering algorithms on synthetic datasets

3.2 UCI数据集实验结果

本节选取4个UCI数据集用于算法性能测试。表5为AMDFC与各对比算法的评价指标比较。其中，Iris数据集分布相对均匀，因此在该数据集上AMDFC 算法性能略低于对比算法，但仍较好地完成了数据集的划分。E-coli 数据集密度分布不均匀，适合使用本文提出的算法进行处理，实验结果表明AMDFC 在E-coil 数据集上三项指标均达到最优。同样的，AMDFC 算法在Heart failure clinical数据集上聚类精度达到最优，在Banknote authentication 数据集上聚类精度与标准化互信息最优。综上，AMDFC方法在处理任意形状与非均匀密度数据集时表现出了优异的聚类性能。

表5 各聚类算法在UCI数据集上的评价指标对比Table 5 Comparison of evaluation indicators of various clustering algorithms on UCI datasets

4 结束语

针对密度峰值聚类算法存在的不足，提出一种自适应多密度峰值子簇融合聚类算法。第一，将自然邻居的概念引入密度峰值聚类算法中，在计算局部密度时考虑样本点的邻域信息，自然邻居具有的自适应特点解决了参数敏感的问题。第二，针对密度分布稀疏簇的中心点不易被发现的问题，提出一种聚类中心点自动选取策略，通过扩大选取范围来尽量使得所有簇的中心都被选取。第三，在非中心点的分配阶段，使用两阶段分配策略，通过对稠密点进行首次分配形成聚类雏形，降低了分配过程中连锁反应出现的概率。第四，由于聚类中心的选取范围扩大，生成的簇数大于真实簇的数量，因此定义了一种K近邻相似度计算子簇间的相似度，并将相似度高的子簇进行融合，生成最终聚类结果。实验结果表明，AMDFC算法可以很好地对任意形状及非均匀密度数据集进行聚类。下一步的工作重点是将该算法应用到高维复杂数据以及流数据环境中，适配更多的实际应用环境。