基于BP神经网络的鸡蛋货架期和贮藏时间预测模型研究

陆逸峰，何子豪，曾宪明，徐幸莲，韩敏义,*

（1.南京农业大学 肉品加工与质量控制教育部重点实验室，江苏 南京 210095；2.温氏食品集团股份有限公司，广东 云浮 527400）

鸡蛋由于富含蛋白质、维生素、脂肪和矿物质等营养物质而受到消费者的喜爱，被誉为人类理想的营养库[1-2]。因为受到各种因素的影响，如温度、湿度、鸡蛋品种、蛋鸡饲养环境等，鸡蛋的货架期缺乏统一的标准[3]。哈夫单位、气室高度、蛋黄指数、蛋清pH值和质量损失率等是表征鸡蛋新鲜度的重要指标，常被应用于鸡蛋货架期的预测[4-5]。建立货架期模型有助于减少鸡蛋贮藏时间过长造成的损失，保障上市鸡蛋品质[6]。同时由于鸡蛋品质在贮藏过程中受环境因素的影响很大[7]，原始保质期不一定准确，通过货架期模型预测出的数值可以用于检验原始保质期是否准确，确保在保质期内销售的鸡蛋品质合格从而减少消费者的投诉。此外，一些不良商家为了自己的利益，在商品即将超过保质期的时候，通过蓄意篡改生产日期、标注虚假生产日期来欺骗消费者，这些行为不仅违反市场秩序和国家法律法规，而且会误导消费者，使其合法权益受到侵害[8]。基于以上原因，迫切需要一种快速、准确的方法来监测鸡蛋在不同贮藏温度下的新鲜度变化以及预测贮藏时间。通过构建一个鲁棒模型预测鸡蛋已经贮藏的时间，有助于鉴别生产商标注的生产日期是否真实可靠[9]。

目前应用于鸡蛋货架期预测的模型大致分为两类，一是传统的基于单一指标预测的动力学模型，如刘钰等[10]构建了不同涂膜方式的鸡蛋货架期预测动力学模型，并根据NY/T 1758—2009《鲜蛋等级规格》成功对鸡蛋的货架期进行了预测；李龙等[11]研究了鸡蛋在4、10、16、37 ℃下新鲜度指标变化规律，基于哈夫单位的货架期预测模型预测效果较好，相对误差在10%以内。二是新兴的机器学习模型，如人工神经网络（artificial neural network，ANN）、偏最小二乘回归（partial least squares regression，PLSR）算法和支持向量回归（support vector regression，SVR）算法等，它们可以通过综合多个指标共同作用来提高预测的准确性。刘雪等[4]构建了基于BP神经网络（back propagation artificial neural network，BPANN）的鸡蛋货架期预测模型，并与动力学模型进行对比，发现BP-ANN预测精度更高，准确率达到95.93%。在其他食品货架期的预测上，如苹果[6]、腌制火腿[12]、松茸[13]、葡萄[14]等，人工智能算法已经展现出了优越的性能。不过目前将其应用于鸡蛋剩余货架期预测的研究较少，且大都限于研究同一因素（贮藏温度、鸡蛋品种、预测模型）对鸡蛋货架期的影响。郭春燕等[15]研究发现不同品种的鸡蛋哈夫单位存在显著性差异。陈健锋等[16]测定了不同贮藏温度下鸡蛋的新鲜度及微生物变化情况，结果表明贮藏温度对鸡蛋品质具有极大的影响。因此，迫切需要构建一种基于多个影响因素的机器学习模型，实现对鸡蛋货架期的精准全面预测。此外，大多数预测鸡蛋贮藏时间的研究主要限于通过分类模型区分不同贮藏时间的鸡蛋，对于建立回归模型进行预测的情况，国内外仍然鲜有研究。刘明等[17]使用电子鼻分析了鸡蛋贮藏过程中产生的气味，通过主成分分析、线性判别等多元统计方法区分了不同贮藏时间的鸡蛋，取得了较好的效果。Li Jiating等[5]将电子鼻与概率神经网络相结合对不同贮藏时间的鸡蛋进行了分类，预测集的样本准确率为92.86%。

由于目前关于鸡蛋货架期预测的研究大部分都基于单一品种鸡蛋和传统动力学模型展开[10,18-19]，鲜有针对于相同实验条件下，不同新型机器学习模型对不同贮藏温度、不同品种鸡蛋货架期和贮藏时间的预测研究。因此，本实验系统性地研究不同品种鸡蛋贮藏于不同温度条件下的货架期，并将新鲜度指标作为输入参数构建基于BP-ANN的鸡蛋货架期和贮藏时间预测模型。以表征鸡蛋新鲜度最重要的指标哈夫单位为模型固定输入参数，其余输入参数的确定则基于Pearson相关性分析结果，依据其与哈夫单位的关联强度，依次作为输入参数构建预测模型。根据模型在预测集上的表现以确定最优输入参数，并对隐含层神经元个数进行优化，最后将最优模型与其他多指标预测模型如PLSR和SVR进行对比。以期为鸡蛋在不同贮藏温度下的货架期制定提供参考，为剩余货架期和贮藏时间的快速、准确、同步预测提供技术支持。此外，通过对贮藏时间的预测，可以间接推断出鸡蛋的生产时间，为解决标注假生产日期、篡改生产日期等问题提供一定的参考。

1 材料与方法

1.1 材料

取产下24 h以内的鸡蛋。‘京粉6号’鸡蛋产自广西省梧州市温氏胜洲蛋鸡场64 周龄蛋鸡，以下简称为京粉；‘海兰灰’鸡蛋产自广西省梧州市温氏胜洲蛋鸡场56 周龄蛋鸡，以下直接称为海兰灰。

1.2 仪器与设备

EA-01蛋品质分析仪 美国ORKA公司；雷磁PHS-3E pH计 上海仪电科学仪器股份有限公司；游标卡尺（精度0.01 mm） 中国得力集团有限公司；DTT-A1000电子天平 福建华志电子科技有限公司；304蛋清分离器 杭州拜杰科技有限公司。

1.3 方法

1.3.1 鸡蛋的贮藏

将鸡蛋分别置于冷藏（4 ℃冷库）以及常温（25±3）℃条件下，常温鸡蛋每2 d进行理化指标的测定，冷藏鸡蛋每6 d测定一次，每个指标进行4 次平行实验。根据我国现行分级标准以及美国农业部鸡蛋标准规定[20-21]，鸡蛋哈夫单位低于60（货架期终点）后结束测定。

1.3.2 指标测定

1.3.2.1 哈夫单位

使用蛋品质分析仪测定哈夫单位。

1.3.2.2 气室高度

参考饶珏睿等[22]的方法，使用自制精度为1 mm贴合鸡蛋外壳的气室高度测量规尺进行测量。

1.3.2.3 蛋黄指数

参考马逸霄等[23]的方法并略有修改。将鸡蛋横向磕破后，使用蛋清分离器将蛋清与蛋黄分离，蛋黄倒于水平放置的玻璃板上。将牙签插入蛋黄内部至最深处，然后使用游标卡尺测量被蛋液没过的牙签部分，所得结果为蛋黄高度。再使用游标卡尺测量蛋黄横向直径与纵向直径，记录结果取平均值即为最终蛋黄直径，蛋黄指数按公式（1）计算。

式中：Y为蛋黄指数；H为蛋黄高度/mm；Q为蛋黄直径/mm。

1.3.2.4 蛋清pH值

使用蛋清分离器分离蛋清于烧杯中，用玻璃棒将蛋清搅拌均匀，采用pH计测定蛋清pH值，直至pH计数值不发生变化后记录数值。

1.3.2.5 质量损失率

选取4 个鸡蛋进行编号，记录其初始质量（m1）和贮藏过程中的质量（mi）。质量损失率按公式（2）计算。

1.3.3 回归模型构建与模型评价

随机将（4＋4）×8＝64 个常温鸡蛋样本和（4＋4）×15＝120 个冷藏鸡蛋样本数据依据7∶1.5∶1.5的比例划分为训练集、验证集和预测集。利用BP-ANN、PLSR和SVR建立鸡蛋货架期和贮藏时间预测模型。

回归模型建立之后，通过预测集决定系数（coefficient of determination of the prediction set，、预测集均方根误差（root mean square error of the prediction set，RMSEP）和平均绝对误差（mean absolute error，MAE）来评价模型的预测效果，计算分别见公式（3）～（5）。

式中：np为预测集的样本数；ypi为预测集中第i个样本的实际值；为预测集中第i个样本的预测值；表示预测集中所有样本实际值的平均值。

越大，代表回归模型的拟合效果越好；RMSEP和MAE越小，代表模型的预测误差越小。

1.4 数据处理与分析

采用Origin 2019b软件进行图形绘制，利用SPSS 25软件进行Pearson相关性分析，利用Matlab R2020a软件中的神经网络工具箱（Neural Net fitting）构建及训练BP-ANN，利用The Unscrambler X 10.4软件构建PLSR模型和SVR模型。

2 结果与分析

2.1 鸡蛋在贮藏过程中新鲜度变化

2.1.1 鸡蛋在不同贮藏温度下哈夫单位的变化趋势

由图1可知，在常温条件下，两种鸡蛋的哈夫单位随时间延长而下降，在前3 d下降速度快，随后减缓，在第13天均下降至60以下，京粉和海兰灰分别为52.42和53.14，故两种鸡蛋的常温货架期为12 d左右。该实验结果与刘钰等[10]预测鸡蛋在22 ℃、相对湿度65%下的一级蛋货架期为10～27 d一致。在冷藏条件下，两种鸡蛋的哈夫单位均在第84天下降至60以下，故冷藏货架期为83 d左右。此外，鸡蛋在冷藏条件下哈夫单位下降趋势明显慢于常温条件下，表明贮藏温度对哈夫单位的影响极大，鸡蛋在低温条件下贮藏品质更好，有利于延长货架期。

图1 常温及冷藏条件下鸡蛋哈夫单位变化Fig. 1 Trends in egg Haugh unit at 25 or 4 ℃

2.1.2 鸡蛋在不同贮藏温度下气室高度的变化趋势

气室高度是反映鸡蛋新鲜程度的指标之一，气室高度越小，鸡蛋越新鲜。由图2可知，常温贮藏时，两种鸡蛋的气室高度随时间延长而上升，与薛艳蓉等[24]的研究结果一致；两种鸡蛋的气室高度在前3 d快速上升，随后上升趋势减缓，京粉和海兰灰在第14天时分别增至5.09 mm和5.16 mm。在冷藏条件下，两种鸡蛋的气室高度在前6 d剧烈上升，在第84天京粉和海兰灰气室高度分别上升至6.97 mm和7.09 mm。

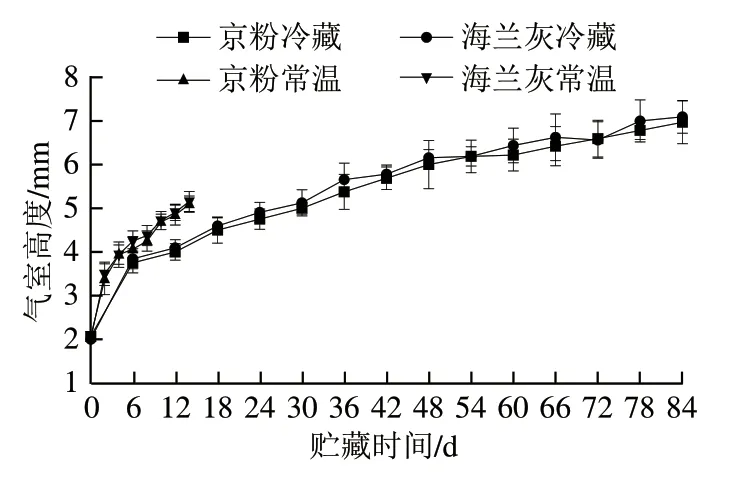
图2 常温及冷藏条件下鸡蛋气室高度变化Fig. 2 Trends in egg air cell depth at 25 or 4 ℃

2.1.3 鸡蛋在不同贮藏温度下蛋黄指数的变化趋势

在贮藏过程中，蛋黄指数会逐渐降低，这是由于鸡蛋内蛋黄膜的弱化和蛋清中的水分向蛋黄迁移[25]。由图3可知，常温贮藏时，两种鸡蛋的蛋黄指数随时间延长而剧烈下降，在第14天时京粉和海兰灰分别下降至0.340 3和0.338 8；而在冷藏条件下，在第84天两者蛋黄指数分别降至0.394 5和0.391 9。该实验结果与吉小凤等[18]报道的蛋黄指数变化趋势一致。

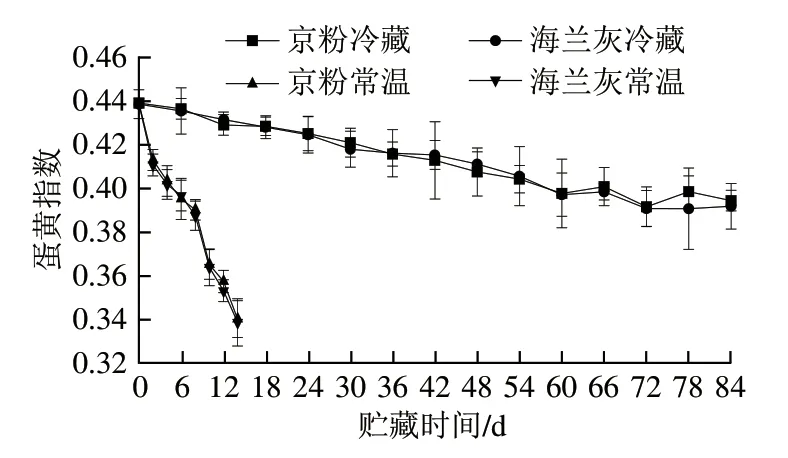
图3 常温及冷藏条件下鸡蛋蛋黄指数变化Fig. 3 Trends in egg yolk index at 25 or 4 ℃

2.1.4 鸡蛋在不同贮藏温度下蛋清pH值的变化趋势

由图4可知，在常温贮藏下，两种鸡蛋的蛋清pH值在前3 d快速上升，随后上升趋势减缓，可能是因为在贮藏前期鸡蛋呼吸强度较大，导致内部大量CO2从气孔逸出[2]，之后呼吸强度减弱[26]。京粉和海兰灰蛋清pH值在第14天分别上升至9.50和9.46。该结果与饶珏睿等[22]发现在（25±3）℃条件下鸡蛋蛋清pH值在前4 d显著上升一致。在冷藏条件下，京粉和海兰灰蛋清pH值在第84天分别上升至9.32和9.35。

图4 常温及冷藏条件下鸡蛋蛋清pH值变化Fig. 4 Trends in albumen pH at 25 or 4 ℃

2.1.5 鸡蛋在不同贮藏温度下质量损失率的变化趋势

鸡蛋在贮藏过程中质量损失率上升是由于水分蒸发和CO2从蛋壳中逸出。从图5可知，常温贮藏14 d时，京粉、海兰灰质量损失率分别上升至2.68%、2.35%，造成差异的原因可能是鸡蛋品种和蛋鸡的周龄不同。在冷藏条件下，京粉和海兰灰质量损失率在第42天分别上升至4.96%和5.09%。结果表明，低温贮藏可以延缓质量损失率上升趋势，该结论与杜丹萌等[27]的研究一致。

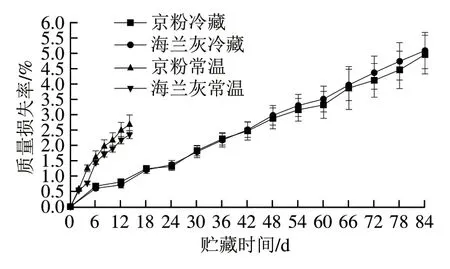
图5 常温及冷藏条件下鸡蛋质量损失率变化Fig. 5 Trends in egg mass loss percentage at 25 or 4 ℃

2.2 Pearson相关性分析

由于BP-ANN的输入参数个数对预测结果具有较大的影响，如果输入参数过多，会增加计算量，使训练速度变慢；而输入参数过少，模型预测的准确性会受到影响[28]。因此，通过Pearson相关性分析优化输入参数，找出与哈夫单位关联强度较高的其他新鲜度指标作为模型的输入参数，可在减少模型运算量的同时提高预测的精确性。

由表1、2可知，在常温条件下，哈夫单位与各指标间均极显著相关，相关性从高到低依次排序为：蛋黄指数＞质量损失率＞气室高度＞蛋清pH值；在冷藏条件下，哈夫单位与各指标也均极显著相关，相关性从高到低依次排序为：质量损失率＞气室高度＞蛋黄指数＞蛋清pH值。

表1 常温条件下新鲜度指标相关性Table 1 Correlation analysis between freshness indices of eggs stored at 25 ℃

表2 冷藏条件下新鲜度指标相关性Table 2 Correlation analysis between freshness indices of eggs stored at 4 ℃

2.3 回归模型的构建

以哈夫单位为模型固定输入参数，其余输入参数的选择基于相关性分析结果，即以与哈夫单位的相关性由高到低的指标依次作为模型的输入参数，如表3所示，分别构建了不同贮藏温度下输入参数个数为1～5的BP-ANN鸡蛋货架期预测模型与贮藏时间预测模型。

表3 模型输入参数选择Table 3 Input parameter selection for the model

验证集中的样本用于调整模型的超参数，如人为设置的学习率、训练次数等，并对模型能力进行初步评估。预测集的数据从一开始就被划分出来，不参与网络的训练。它被用来测试训练后的网络在新数据上的泛化能力[29-30]。

BP-ANN是一种多层前馈神经网络[31]。典型的BP-ANN层与层之间全连接[32]，包括1 个输入层、1 个输出层和至少1 个隐含层[33]（图6）。BP-ANN的主要特点是信号的正向传播和误差的反向传播。在正向传播中，信号处理是在逐层处理的基础上进行的，即信号从输入层传播到隐含层，再传播到输出层[13]。如果在输出层没有获得期望的输出，信号就会反向传播，并根据预测误差调整网络权值和阈值，使BP-ANN的预测输出逐渐接近其期望输出[34]。在本研究中，哈夫单位为默认输入参数，其余输入参数个数由1至5逐渐叠加，依次作为模型的输入参数构建模型。输出参数为剩余货架期和贮藏时间。隐含层层数为1，神经元数的选择依据公式（6）。网络参数和函数为matlab神经网络工具箱中的默认参数。

图6 BP-ANN结构图Fig. 6 Structure chart of BP-ANN

式中：N为隐含层神经元数；a为输入层神经元数；b为输出层神经元数；c为[1,10]之间的常数。

PLSR算法是一种常用的化学计量学方法，可以同时实现回归建模、数据结构简化以及解决变量间的多重相关性等问题[35-37]。SVR算法常被用于多元建模分析，其原理是将原问题通过一系列非线性变换转化为高维空间的线性问题，并在高维空间中进行线性求解，从而解决多个特征因子的回归问题[38-39]。本实验选择这两种算法构建回归模型，与优化后的BP-ANN算法进行预测性能对比。

2.3.1 货架期预测模型

输入参数个数为1～5时各模型在训练集及预测集上的预测结果如图7所示。根据模型在预测集上的表现来评价模型的最终性能，发现在常温条件下，输入参数个数为1，即哈夫单位时，BP-ANN预测效果最差，较低，RMSEP较高，分别为0.883 4和1.458 4；当输入参数个数为2～5时，各模型的均在0.90以上，具有较好的拟合优度。其中，当输入参数个数为2、3和5时，各模型的预测误差较小，RMSEP小于1，MAE小于0.65 d。在冷藏条件下，发现输入参数为哈夫单位时，BP-ANN预测效果最差（＝0.895 4，RMSEP＝7.544 0）；而当输入参数个数为2～5时，各模型的均在0.97以上，RMSEP小于4，MAE小于3 d。该结果表明BP-ANN在预测鸡蛋剩余货架期上具有一定的可行性，且当输入参数为单一指标时模型预测效果不佳，多指标综合预测可以有效提升模型的预测精度。

通过对比不同输入参数个数下BP-ANN货架期预测模型，得到以下结论：在常温条件下，当输入参数个数为3，即以哈夫单位、蛋黄指数和质量损失率为参数时，BP-ANN预测性能以及拟合效果达到最佳，RMSEP和MAE分别为0.988 2、0.478 5和0.350 9 d。故选择输入参数个数为3，即以哈夫单位、蛋黄指数和质量损失率为参数时所构建的BP-ANN进行后续的研究。在冷藏条件下，当输入参数个数为3时，BP-ANN拟合优度最好，预测误差也最小，RMSEP和MAE分别为0.986 3、3.005 2和2.280 1 d。因此，选择输入参数个数为3，即以哈夫单位、气室高度和质量损失率为参数所构建的BP-ANN进行后续的研究。随后对隐含层神经元数进行优化，如表4所示，发现当隐含层神经元数分别为5和10时，常温和冷藏条件下的BP-ANN鸡蛋货架期模型预测性能最佳。

表4 BP-ANN隐含层神经元数优化Table 4 Optimization of the number of neurons in the hidden layer of BP-ANN

将上述获得的基于BP-ANN的最佳鸡蛋货架期模型与其他机器学习模型对比，结果见表5。经过相同训练集训练，模型在同一预测集上的表现代表了最终的预测性能。一般来说，一个好的多元模型具有较高的Rp2和较低的RMSEP、MAE。相较于SVR和PLSR，优化隐含层神经元数后的BP-ANN对鸡蛋剩余货架期预测效果更佳。在常温条件下，当输入参数为哈夫单位、蛋黄指数和质量损失率，隐含层神经元数为5时，BP-ANN的预测表现最佳（＝0.988 2，RMSEP＝0.478 5），SVR表现次之＝0.987 0，RMSEP＝0.512 9），PLSR预测误差较大＝0.937 5，RMSEP ＝1.229 0）；在冷藏条件下，当输入参数为哈夫单位、气室高度和质量损失率，隐含层神经元数为10时，BP-ANN预测精度最高（＝0.986 3，RMSEP＝3.005 2），PLSR预测精度最低（＝0.974 8，RMSEP＝3.589 9）。此外，图8A、B可以反映出预测模型在数据集上MAE的表现，无论是冷藏还是常温条件下，BP-ANN在数据集上MAE的整体表现优于PLSR和SVR，对鸡蛋剩余货架期的预测误差较小。由图8C、D可知，BP-ANN在整个数据集上的MAE低于PLSR和SVR，对鸡蛋贮藏时间的预测误差较小。

图8 不同预测模型绝对误差对比Fig. 8 Comparison of absolute errors of different prediction models

2.3.2 贮藏时间预测模型

如图9A所示，在常温条件下，当输入参数为哈夫单位时，BP-ANN预测效果最差（＝0.907 2，RMSEP＝1.262 0）；当输入参数个数为2～4时，各模型的Rp2均在0.96以上，具有较好的拟合优度。如图9B所示，在冷藏条件下，输入参数为哈夫单位时，BP-ANN预测效果最差（＝0.888 0，RMSEP＝9.422 5）；而当输入参数个数为2～5时，各模型的均在0.95以上，RMSEP小于6，MAE小于4 d，表明BP-ANN在预测鸡蛋贮藏时间上具有一定的可行性，多指标预测模型预测精度明显高于单一指标预测模型。通过对比输入参数个数为1～5时BP-ANN贮藏时间预测模型，结果表明，在常温条件下，当输入参数个数为2，即哈夫单位和蛋黄指数时，BP-ANN预测性能以及拟合效果最佳，RMSEP和MAE分别为0.989 4、0.512 0和0.369 6 d。因此，选择输入参数个数为2，即选择哈夫单位和质量损失率作为输入参数所构建的BP-ANN进行后续的研究。在冷藏条件下，当输入参数个数为2时，BP-ANN预测误差最小，RMSEP和MAE分别为0.983 1、3.518 4和3.621 2 d。因此，选择输入参数个数为2（哈夫单位和质量损失率）时所构建的BP-ANN进行后续的研究。通过对隐含层神经元数的优化，如表4所示，当隐含层神经元数分别为3和7时，BP-ANN在常温和冷藏条件下预测表现分别取得最佳。

图9 不同输入参数个数的BP-ANN鸡蛋贮藏时间预测模型Fig. 9 Prediction models for egg storage time based on BP-ANN with different numbers of input parameters

最后将经过优化后的BP-ANN鸡蛋贮藏时间预测模型与其他机器学习模型对比，结果见表5。无论是在常温还是冷藏条件下，相较于PLSR和SVR，BP-ANN在同一预测集上的预测效果均为最佳。在常温条件下，输入参数为哈夫单位和蛋黄指数、隐含层神经元数为3时，BP-ANN的预测精度最高，和RMSEP分别为0.989 4和0.512 0，而此时PLSR和SVR的分别为0.973 7和0.974 6，RMSEP分别为0.804 0和0.790 5。在冷藏条件下，输入参数为哈夫单位和质量损失率、隐含层节点数为7时，BP-ANN的和RMSEP分别为0.983 1和3.518 4，对鸡蛋贮藏时间的预测表现优于PLSR（＝0.976 1，RMSEP＝3.90 7）和SVR（＝0.972 7，RMSEP＝5.60 7）。

3 结 论

以哈夫单位低于60所对应贮藏时间作为京粉和海兰灰货架期的终点，本研究中京粉和海兰灰两种鸡蛋在常温和冷藏条件下的货架期分别为12 d和83 d。

对常温和冷藏条件下的5 个新鲜度指标数据进行了相关性分析，依据各指标与哈夫单位间的关联强度，依次构建了输入参数个数为1～5的BP-ANN货架期和贮藏时间预测模型。根据模型在预测集上的表现确定最优输入参数，并对隐含层神经元数进行优化，最后将获得的最优BP-ANN模型与PLSR、SVR模型进行性能对比。结果表明，在常温和冷藏条件下，经过优化隐含层神经元数的BP-ANN对鸡蛋剩余货架期和贮藏时间的预测精度最高。在常温条件下，输入参数为哈夫单位、蛋黄指数和质量损失率时，对鸡蛋剩余货架期的预测性能最佳（＝0.988 2，RMSEP＝0.478 5）；输入参数为哈夫单位和蛋黄指数时，对贮藏时间的预测误差最小（＝0.989 4，RMSEP＝0.512 0）。在冷藏条件下，当输入参数为哈夫单位、气室高度和质量损失率时，货架期预测模型预测效果最佳（＝0.986 3，RMSEP＝3.005 2）；输入参数为哈夫单位和质量损失率时，贮藏时间预测模型具有较高的预测精度（0.983 1，RMSEP＝3.518 4）。该结论表明通过鸡蛋当前的品质状况，应用化学计量学方法预测剩余货架期和贮藏时间具有一定可行性，可为在预测鸡蛋剩余货架期和贮藏时间的相关研究提供一定的参考。