一种基于FPGA 的二维精密伺服控制系统设计

［王振 杨乾远 王琛 刘金标 蒋祖运 申永］

伺服转台作为无线光通信中跟瞄系统的重要组成部分，作用是执行对信标的搜索、跟踪和对准[1～2]，随着无线光通信技术在航空、航天领域不断深入，对伺服控制的精度和性能在不断提高[3],目前大多采用串行结构的单片机[4]或DSP[5～6]实现，对多轴系统支持不足，存在的一些FPGA 方案，或与DSP 协同完成、或算法复杂，降低了实时性和精度，易产生振荡，因此急需一种纯硬件描述语言实现的高效伺服系统。高效的伺服控制必须以约10～100 kHz 的速率循环执行矢量控制算法[7]，FPGA 能以百万赫兹并行执行算法、采集数据、实时控制和处理通信，效率远高于微处理器，是伺服控制的最佳选择；系统以三相直流无刷电机为控制对象，设计一种基于FPGA 的二维伺服控制系统，并进行了实验，取得了优良效果，对高精度、高性能跟瞄系统的研制有十分重要的意义。

1 系统总体设计

1.1 控制系统组成

控制系统主要由控制系统、方位和俯仰伺服电机、三相逆变器桥、三相电流采集模块和编码器组成，系统组成如图 1 所示。

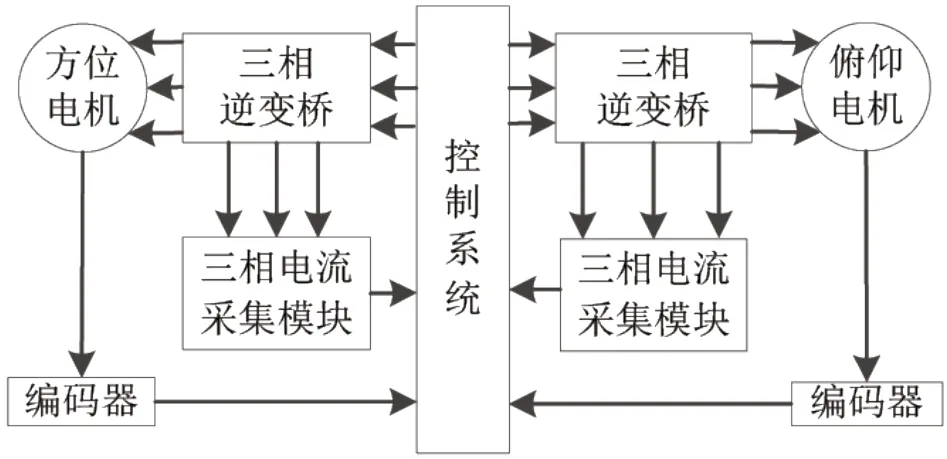
图1 系统组成框图

控制器选择Altera 公司型号为EP3C40F324 的FPGA，用于算法执行、编码器解码以及PWM 产生等功能。三相逆变桥选择TI 公司的驱动器DRV8312，体积小、驱动力大。电流采集模块选择CROSS-CHIP 公司的霍尔效应电流传感器CC6902，在5 V 电压输入下，输出在0.2～4.8 V 间线性变化。编码器采用SPI 接口24 bit 高分辨率绝对式光栅编码器。电机参数，额定电压24 V，额定电流3.3 A，极对数4，额定力矩0.315 N.m，转动惯量0.135 kg.CAm²，额定转速3 600 r/min。

1.2 控制系统设计

要实现二维伺服系统对激光信标快速且精确的跟踪和对准，控制系统需要设计电流环、速度环和位置环[8]，控制原理如图2 所示，从内到外分别为电流环；速度环和位置环；电流环的作用是改善系统动态性能，速度环的作用是提高伺服转台平稳性，位置环的作用是及时反馈位置信息并快速精确地跟踪定位[9]。速度环和位置环简单，不需要解耦控制参数，可根据调试效果选取PI 控制参数，因此主要论述电流环的实现。

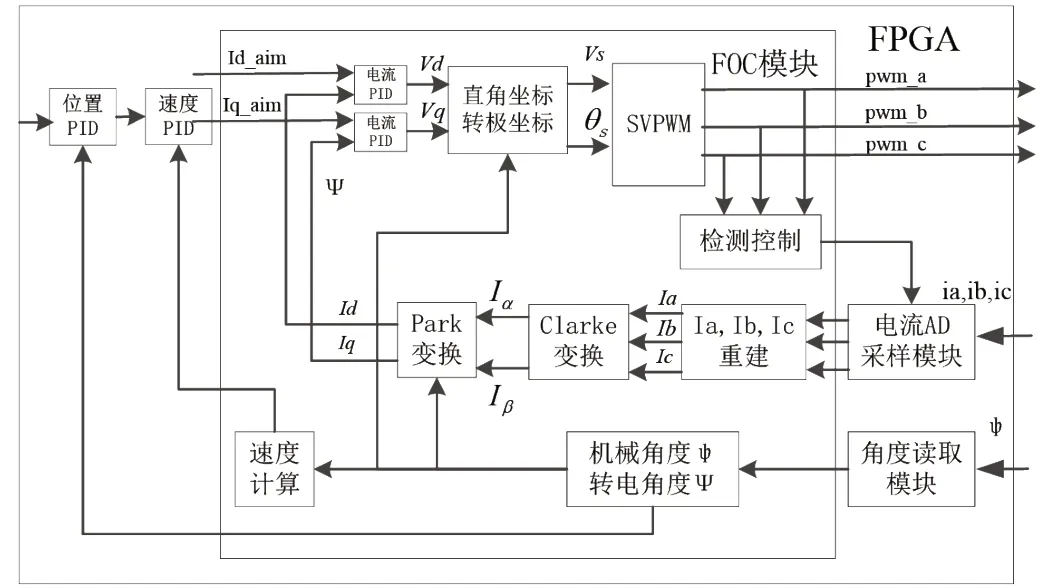
图2 控制原理图

系统实现了极坐标系下的伺服控制参数的解耦，降低了控制复杂度，并进行了优化设计。根据自顶向下设计原则，对进行模块划分，在顶层例化功能模块，进行仿真和实验验证；模块包括：坐标变换模块、极坐标系转换模块、SVPWM 调制模块。

2 控制算法设计

控制系统主要包含clarke 变换、park 变换、极坐标系转换模块和SVPWM 调制子模块。为了提高电机工作效率，设置励磁电流id=0[10]，使定子电流全部用于产生转矩。

2.1 坐标变换

2.1.1 Clark 变换

如图 3 所示为Clarke 变换[11]，将三相时变系统(ia,ib,ic)投影转换为两相时变系统(iα,iβ)，减少一个控制维度，降低控制复杂度。假设a轴和α轴重合，三相信号(ia,ib,ic)由相隔120°的三个不同轴表示，经过Clarke变换后，向量的投影便可以仅由两个正交分量(i α,iβ)

根据图3 的投影原理，利用求解该系统的矩阵乘积，直接得出转换公式：

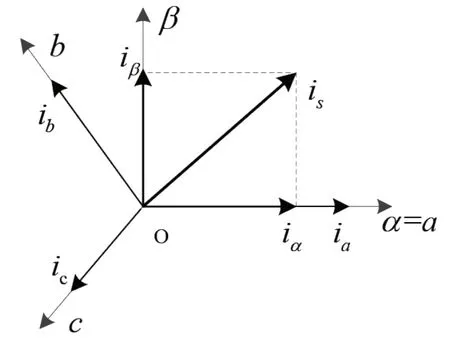
图3 Clarke 变换和投影

式（1）仍然是时变的，但减少了一维变量。由于FPGA 不善于算术运算，更适合移位运算，因此，给等式左右都乘来消除除法,再利用麦克劳林公式逼近。

我国苜蓿的单产水平与加拿大、美国等国家相比相对较低，究其原因施肥技术不成熟。我国苜蓿生产中普遍存在不施肥现象，在苜蓿施肥方面的研究不足，即便施肥，盲目性也很大[5,16]。因此，定期测定土壤肥力以确定苜蓿是否施肥和施用何种肥料必要而科学。近年来，有关苜蓿在肥料配施对其鲜干草产量、农艺性状、品质和生产性能等方面的影响的研究较多，且这些研究也多见于河北、吉林、新疆、宁夏等地区[5,14-15,17]。

用麦克劳林级数公式逼近(1 +2)1/2得：

上述处理方法的性质不变，但可在FPGA 中计算，且提高了运算速度，与查表法相比，该方法可增加展开项得到任意精确位数。

2.1.2 Park 变换

如图4 所示为Park 变换[11]，将Clarke 变换输出的正交时变系统(iα,iβ)转换为两相旋转时不变系统(id,iq)，可降低控制复杂性，要求d 轴与转子磁通对齐。

图4 Park 变换及其正交投影

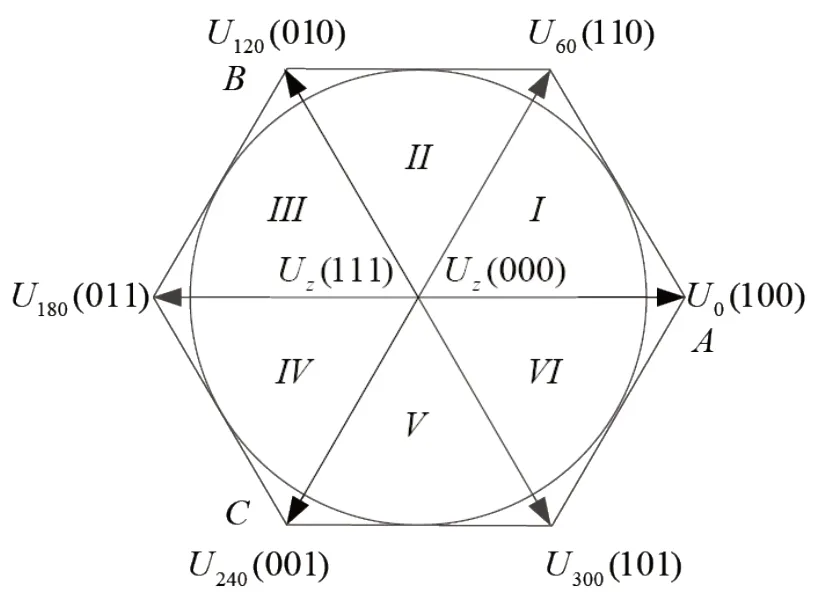
图5 基本电压空间矢量

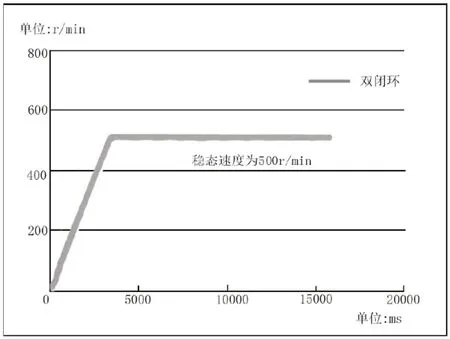
图6 电机闭环启动速度曲线

图7 改变指令后的速度响应曲线

利用投影原理可以得出转换公式。

式（2）中，θ是转子磁通位置，设d 轴与转子磁通对齐，为旋转时不变系统，公式涉及到乘加运算和角度的正余弦计算，常用的正余弦查找表法精度受FPGA 资源限制，对24bit 的编码器不能满足要求，采用FPGA 的CORDIC(Coordinate Rotation Digital Computer)的数字旋转模式，利用移位及加/减算术运算来直接完成矢量旋转变换，CORDIC 算法旋转模式比较均衡，计算速度快和精度高，且适合于用数字硬件实现。

2.2 电压的K/P 变换

用电压矢量的模和角度代替d 轴和q 轴分量对电机进行控制，有助于减少控制过程中的系统元件，简化控制过程并减少控制的执行时间。设极坐标系的电压矢量幅值为ρ，极坐标系的电压矢量角度为θ，id和iq为旋转直角坐标系中d 轴和q 轴分量的分量，速度环输出的电流送入电流PI 控制器得到电压值vd和vq，vd和vq为直角坐标系中的点，则直角坐标系到极坐标系的变换（K/P 变换）为：

式（4）分母vd易溢出，进一步处理：

利用cordic 算法的向量模式实现从直角坐标系到极坐标的转化得到ρ和θ，cordic 算法空间占用少，计算速度快，然后将ρ和θ输出给SVPWM 模块。

2.3 极坐标下SVPWM 的Verilog 实现

上一节得到SVPWM 的输入控制量ρ和θ，ρ为参考电压矢量Uref，θ为参考电压矢量移相角，以ρ和θ正弦函数值控制调制过程。

2.3.1 矢量作用时间分析

极坐标下电压矢量所在扇区由θ得到，首先确定相邻两个基础矢量作用时间。如图 5 所示，六个矢量下标表示其在矢量圆中位置[12]，括号中数表示开关状态，8 个基础矢量U0(100)、U60(110)、U120(010)、U180(011)、U240(001)、U300(111)、U300(101)、Uz(000)，其 中Uz(111)、Uz(000) 是零矢量，不产生磁场，用来调制矢量作用时间。

合成的参考电压矢量Uref由所在扇区的两个相邻非零矢量Uk、Uk+1以及零矢量按作用时间比例构成；假设Uk为先作用的有效基础矢量，Uk+1为后作用的有效基础矢量，则Tk为先作用的有效基础矢量的作用时间，Tk+1为后作用的有效基础矢量的作用时间，参考电压矢量Uref的表达式为：

式（5）、（6）中，U0为零矢量UZ(111)、UZ(000)，Ts为调制周期，Tk为矢量Uk作用时间，Tk+1为矢量Uk作用时间，Uk为矢量U0作用时间。基础矢量的扇区对应见表1。

表1 基础矢量扇区对应表

在第一扇区有：

式（7）、（8）为第一扇区Uk和Uk+1的矢量作用时间，θ为参考电压矢量Uref的旋转角度；Udc是逆变器直流电压；其它扇区的Tk和Tk+1可根据投影原理获得。

2.3.2 PWM 占空比计算

在第一扇区中，用周期Ts单位幅值等腰三角波对正弦波信号采样，采样值如下:

式（9）、（10）和（11）中，tk为先作用矢量Uk开始作用时刻，t(k+1)为后作用矢量开始作用时刻，t0为零作用矢量开始作用时刻，θ为参考电压矢量Uref的旋转角度。

设比较参数为Va、Vb和Vc，则有：

式（13）适用于第1、3、5 扇区；式（14）适用于第2、4、6 扇区；

将周期为Ts的单位幅值的等腰三角形锯齿波与比较参数Va、Vb和Vc进行比较，当周期为Ts单位幅值的等腰三角形锯齿波小于Va、Vb或Vc时，所获得SVPWM 调制波对应为低电平；当周期为Ts的单位幅值的等腰三角形锯齿波大于等于Va、Vb或Vc时，所获得的SVPWM 调制波对应为高电平，从而获得第一扇区的SVPWM 调制波，按上述方法，可获得其他五个扇区的SVPWM 调制波。

3 实验验证及结果

根据控制原理图，搭建实验环境，对系统的功能和性能进行验证。实验选择Xilinx 公司的Artix7 系列FPGA，编译环境为Vivado2018.3，采用System Verilog 语言，仿真工具为ModelSim SE-64 10.4。

3.1 闭环稳定性验证

如图 6 所示，速度给定500 r/min，启动电机，电机能从静止状态平滑启动；速度曲线很快稳定到500 r/min。曲线平滑，转矩稳定；稳态误差小。

增大速度指令为800 r/min，如图 7 所示，在9 000 ms时刻稳态进入800 r/min，平稳跟随，转子负载增加或减少，相电流幅值相应增大或减少，系统能够双闭环稳定控制。

3.2 响应时间验证

d 相电流环和q 相电流环的控制参数相同，只需对d相电流环测试验证。d 相电流环输入给定为最大幅值1.5 A。采集电流反馈数据，通过整定增量式PI 算法[13～15]参数。最终测试验证效果，电流环响应时间约为1.6 ms，满足控制要求，与DSP 控制方案[16～17]的电流环响应时间相比，动态性能较好。

3.3 精度对比验证

如图8 所示，分别采用DSP 和FPGA 方案，给定转速为s，在其它相同条件下对比试验，FPGA 方案的控制精度要比DSP 方案高，DSP 的速度误差范围为，FPGA 的速度误差范围为s。

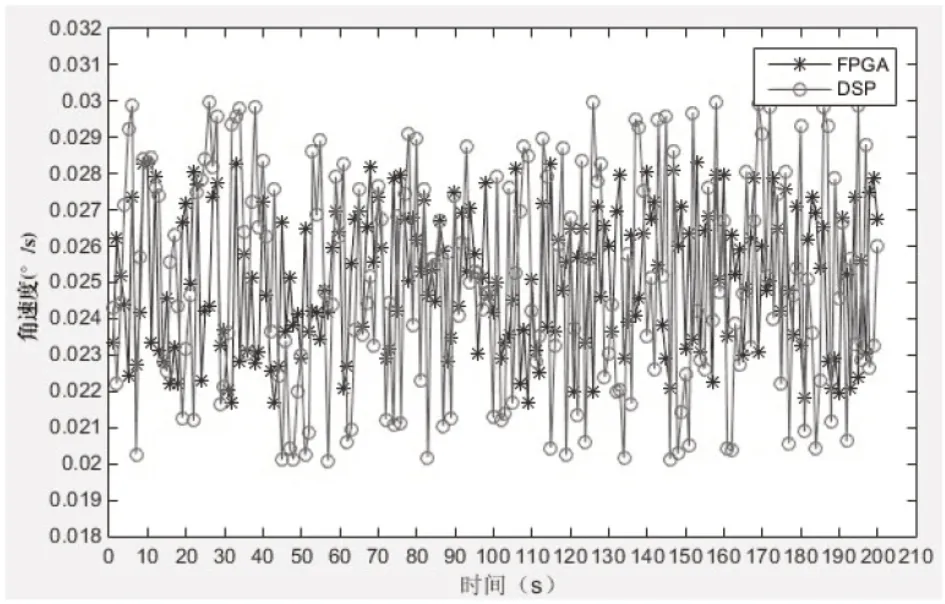
图8 速度对比曲线

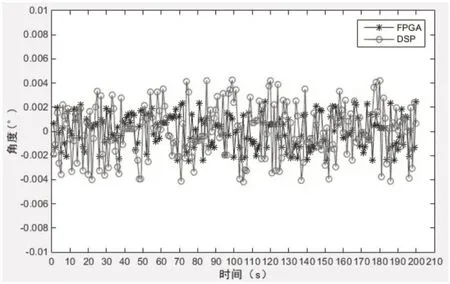
图9 位置对比曲线

如图 9 所示，分别采用DSP 和FPGA 方案，给定位置指令为0，试验得出，FPGA 控制方案的位置控制精度要比DSP 方案精度高，DSP 控制的位置误差在范围为0.008，FPGA 控制的位置误差范围为0.004。

以上对比表明，系统设计的基于FPAG 的电机控制系统在速度和位置控制精度上具有一定优越性，能满足转台控制使用要求。

4 结束语

对无线激光通信中二维伺服控制系统进行了详细设计，并对关键功能和性能指标进行了实验验证，结果表明该二维伺服控制系统结构简单、稳定可靠，实时性强，具有较好的动态性能和静态性能，满足系统设计指标要求，并且该系统的实现有助于减少控制芯片和器件的数量，减小卫星通信设备的体积和重量；对后续研制更高精度和性能伺服系统具有指导意义和参考价值。