Joint Optimization Scheme for the Reconfigurable Intelligent Surface-Assisted Untrusted Relay Networks
2023-12-10LihuaGongWeiXuXiaoxiuDingNanrunZhouQibiaoZhu
Lihua Gong ,Wei Xu ,Xiaoxiu Ding ,Nanrun Zhou,2 ,Qibiao Zhu,*
1 Department of Electronic Information Engineering,Nanchang University,Nanchang 330031,China
2 Shanghai Key Laboratory of Integrate Administration Technologies for Information Security,School of Information Security Engineering,Shanghai Jiao Tong University,Shanghai 200240,China
Abstract: To further improve the secrecy rate,a joint optimization scheme for the reconfgiurable intelligent surface (RIS) phase shift and the power allocation is proposed in the untrusted relay(UR)networks assisted by the RIS.The eavesdropping on the UR is interfered by a source-based jamming strategy.Under the constraints of unit modulus and total power,the RIS phase shift,the power allocation between the confdiential signal and the jamming signal,and the power allocation between the source node and the UR are jointly optimized to maximize the secrecy rate.The complex multivariable coupling problem is decomposed into three sub-problems,and the non-convexity of the objective function and the constraints is solved with semi-defniite relaxation.Simulation results indicate that the secrecy rate is remarkably enhanced with the proposed scheme compared with the equal power allocation scheme,the random phase shift scheme,and the no-RIS scheme.
Keywords: iterative optimization;physical layer security;reconfgiurable intelligent surface;untrusted relay;secrecy rate
I.INTRODUCTION
With the rapid development of communication technology,secure communication based on conventional encryption methods is facing severe challenges.Physical layer security (PLS) exploits the inherent randomness of the channel to ensure secure transmission,which has been widely studied as a supplement or alternative to the upper layer encryption algorithm[1].Recent studies on the PLS are developing,such as cooperative jamming[2,3],holographic MIMO surfaces related to the reconfgiurable intelligent surface (RIS)[4] and cooperative relay technologies [5,6].Cooperative relay improves the coverage of communication networks.However,relay nodes may be honest and curious while actually assisting in communications,since they can forward information,and also have the potential to steal confdiential signals.
Heetalfrist studied the secrecy performance of the untrusted relay(UR)communication network[7].The UR network can still achieve secure transmission.Several endeavors to improve the PLS have been proposed,for example,artifciial noise (AN) and cooperative jamming[8].The latest researches on the security of the UR networks focused on the destinationbased jamming (DBJ) scheme [9].To prevent eavesdropping attacks,the destination transmits a jamming signal to interfere with untrusted relays and eavesdroppers [10].However,the time difference between transmitting and receiving signals at the destination will lead to outdated channel state information (CSI)[11].The source-based jamming (SBJ) scheme combines the jamming signal with the confdiential one,and it effectively overcomes the defciiency of the DBJ scheme [12].The source works as a jammer to generate the jamming signal to hinder the UR from intercepting the confdiential signal.Lv et al.proposed a SBJ scheme to enhance the PLS of the UR networks[13].Half-duplex(HD)transmission has been widely studied in some works.Compared with the HD transmission,full-duplex (FD) transmission is one of the promising techniques that can improve the spectrum effciiency and the secrecy performance[14,15].If the residual self-interference(RSI)is suppressed to a very low level,then the FD mode can increase the multiplexing gain [16].Atapattu et al.studied the secure communication with an FD-UR and further discussed the influence of the RSI on the secrecy rate[17].
With the evolution of metamaterials,a low-cost,energy-effciient device named RIS emerged,offering an effective way to enhance the PLS [18,19].The RIS is composed of reconfgiurable,passive,and reflecting units of compact size,each of which can interact with the incident signal without a dedicated radio frequency processing[20].By adjusting the phase shifts of the reflectors appropriately,the reflected signals can be deliberately strengthened or impaired at the designated nodes [21,22].Zou et al.studied the secure transmission for RIS-assisted wireless communication systems in the presence of eavesdroppers,and the secure energy effciiency is maximized via jointly optimizing the RIS phase reflector as well as the number of RIS elements[23].Feng et al.investigated the PLS enhancement in an RIS-aided secure transmission system.With the presence of an eavesdropper,the active beamforming at the base station and the passive beamforming at the RIS were jointly optimized for secrecy rate maximization [24].Hong et al.suggested exploiting an RIS to enhance the secrecy performance of AN-aided communication systems.To exploit the RIS effciiently,the secrecy rate maximization problem was formulated by jointly optimizing the transmit precoding matrix at the base station,the covariance matrix of AN,and the phase shifts at the RIS[25].
Generally,RIS is deployed on the building surface,indoor wall,and ceiling,which can help eliminate the coverage blind area and increase the connectivity[26].By considering that the relay can be more flexibly deployed anywhere in the cell,the hybrid RISrelay system used by the two devices will become a cost-effective solution in the intelligent electromagnetic environment[27].Nguyen et al.proved that the relay networks assisted by the RIS substantially improve spectral effciiency compared with the conventional RIS-assisted networks [28].Rech et al.proposed a hybrid communication network that utilizes a relay and an RIS to support data transmission over wireless channels,and designed the reflecting coeff-i cients to maximize the achievable rate[29].Huang et al.studied a joint design of relay selection and RIS reflection coeffciient in the RIS-assisted relay networks with an eavesdropper[30].
To the best of our knowledge,the RIS-assisted relay networks have drawn signifciant attention recently.The existing literatures related to this topic focus on the trusted relay scenario [27–29] or the external eavesdropper scenario[30].There is no such study on the RIS-assisted UR networks with cooperative jamming in the existing literatures,which is the motivation of this paper.The main contributions are as follows: (1) The security of the RIS-assisted UR networks is improved by using the SBJ strategy,and a joint optimization scheme for the RIS phase shift and the power allocation is proposed to maximize the secrecy rate.(2)The RIS phase shift,the power allocation between the confdiential signal and the jamming signal,and the power allocation between BS and UR are jointly optimized.The complex multivariable coupling problem is decomposed into three sub-problems,and the iterative optimization algorithm based on the semidefniite relaxation(SDR)is adopted.(3)The numerical results show that the proposed scheme exhibits considerable security advantages over the equal power allocation scheme,the random phase shift scheme,and the No-RIS scheme.
The rest of this paper is organized as follows.The considered system model is introduced in Section II.Then the iterative optimization algorithm based on the SDR is elaborated in Section III.Moreover,simulation results and discussions are demonstrated in Section IV.Finally,a brief conclusion is drawn in Section V.
II.SYSTEM MODEL
As illustrated in Figure 1,the cooperative communication system is composed of a source node (BS),an RIS,a UR,and a destination node(D).The BS and the D nodes are equipped with a single antenna,respectively.The FD-UR is equipped with two antennas(one transmitting antenna and one receiving antenna).The RIS is equipped withMreflecting elements.The FDUR forwards the signals with the decode-and-forward(DF)protocol while attempting to eavesdrop on confidential information.dSI,dSR,dIR,dIDanddRDare defined as the distance between BS and RIS,BS and UR,RIS and UR,RIS and D,and UR and D,respectively.Owing to path loss and blockages,the assumption is that the direct link between BS and D is ignored,such as the urban environment with dense buildings.
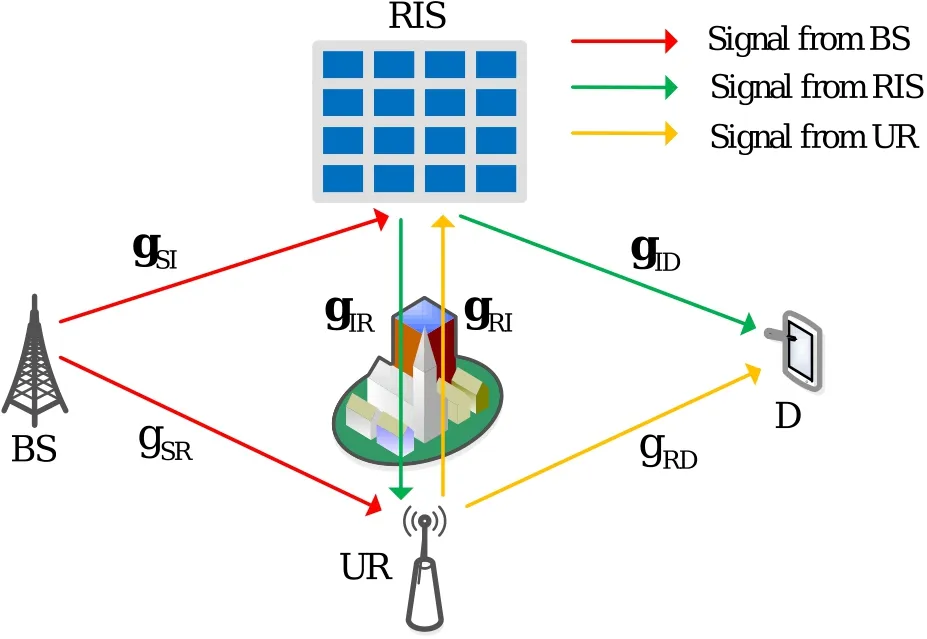
Figure 1.System model of the RIS-assisted UR networks.
2.1 Channel Model
Normally,the BS has sufficient resource to obtain the CSI by using a backhaul link and control the communications in the wireless networks [31].The scalar channels from BS to UR and from UR to D are denoted asgSRandgRD,respectively.The small-scale fading is assumed to be Rayleigh fading due to extensive scatters.Taking the BS-UR as an example,the distance-dependent path loss model is given by,whereρis the path loss at the reference unit distance,kdenotes the path loss exponent.is independent and identically distributed,i.e.,zero mean complex Gaussian random variable with unity variance.The vector channels from BS to RIS and from RIS to D are denoted as gSI∈CM×1and gID∈CM×1,respectively.Similarly,gIR∈CM×1and gRI∈CM×1denote the channels between UR and RIS.For the RIS-related channels,the small-scale fading is assumed to be Rician fading.Specifically,taking the BS-RIS as an example,the small-scale channel can be modeled as
whereεis Rician factor,CM×1are the line-of-sight(LoS)component and nonline-of-sight(NLoS)component,respectively.
The RIS reflects the signal by adjusting the amplitude and the phase.The reflection diagonal matrix at the RIS is as
whereηm∈[0,1]andϑm∈[0,2π]represent the reflection amplitude and the phase shift of them-th reflecting element,respectively.To maximize reflection efficiency,reflection amplitude is usually set toηm=1,∀m.
2.2 Signal Model
At time instantn,the BS transmits the confidential signalx(n) with powerαPSand simultaneously transmits the jamming signalz(n)with power(1-α)PS,whereαis the power allocation factor of the confidential signal and the jamming signal.The FD-UR with the DF protocol forwards the received hybrid signals of the previous blockn-1 to D.Assuming that the powers of the signals reflected by the RIS more than once can be neglected,the received signal at the UR can be given as
whereλSR=PSandPRdenote the transmit power of the BS and the UR,respectively,nRdenotes the additive white Gaussian noise(AWGN)at the UR and followsCN(0,σ2).
The self-interference channel is estimated by calculating the correlation between the received signal and the transmitted one.The received signal-tointerference and noise ratio (SINR) at the UR can be expressed as
whereγRRis the RSI power after self-interference cancellation.The RSI related to the degree of dualantenna interference cancellation follows a Gaussian distribution [32].Accordingly,the received signal at the D node can be represented as
The jamming signal cancellation is assumed perfect,which is a realistic assumption and could be achieved by using pseudo-random or chaotic sequences [17].For example,the jamming signal can be a Gaussian noise generated by a pseudo-random generator with finite states.The BS and the D node apply the same pseudo-random generator,however,the UR does not.Moreover,the channel is assumed quasi-static,and the CSI can be obtained by pilot before data transmission,assisting the jamming signal cancellation at the D node.Consequently,the effect of the jamming signal can be eliminated at D node.Note that the signal at timenis the jamming signal,while timen-1 is the desired signal.Therefore,the received SINR at the D node can be expressed as
Thus,the achieved secrecy rate is expressed as
III.JOINT OPTIMIZATION OF THE RIS PHASE SHIFT AND THE POWER ALLOCATION
3.1 Problem Formulation
Under the constraints of unit modulus and total power,the RIS phase shift and the power allocation are jointly optimized to maximize the achieved secrecy rate.PTis the total power of the system,and the optimization problem can be expressed as OP1:
The optimization variables in the OP1 are highly coupled.The objective function and the constraints are non-convex,which makes the optimization problem more difficult.Generally,no standard method solves such non-convex problems.Therefore,the complex multivariable coupling problem is decomposed into three sub-problems,and the non-convexity of the objective function and the constraints will be solved by the SDR.
3.2 Iterative Optimization
3.2.1 The RIS Phase Shift Design
where vH=[θH,1].Let F=PffH,S=PssH,Q=PqqH,and V=vvH,where V is introduced and used as the optimization variable.According to the nature of the trace,
Similarly,PvHssHv=Tr(SV),PvHqqHv=Tr(QV).After removing the rank-1 non-convex constraint by the SDR and introducing additional exponential relaxation variablest1~t4,the RIS phase shift optimization can be expressed as
OP2:
The non-convex constraint in (12) isαTr(QV)+σ2≤t2and Tr(FV)+γRR+σ2≤t3.Accordingly,a first-order Taylor approximation such thatis adopted.Therefore,OP2 is recast as
At this point,all constraints are convex,and problem OP3 can be solved iteratively using the CVX.Before the iterative algorithm begins,is initialized as
The V obtained by the above algorithm does not necessarily meet the constraint of rank-1,and the result can only be used as the lower bound of the objective function.If the rank is 1,the optimal solution can be obtained by eigenvalue decomposition.If the rank is not 1,the Gaussian randomization method is used to approximate the optimal solution from the high rank V.Firstly,eigenvalue decomposition is carried out V=ΞΛΞH.Ξ and Λ are unitary matrix and diagonal matrix,respectively.Then,the suboptimal solution v*=ΞΛ1/2r is obtained,in which r∈CM×1is randomly generated by the complex Gaussian random distribution with zero mean and variance IM.Finally,the best solution is selected to approximate the optimal value.The optimized phase shiftθ*can be recovered from v*as follows
Such the SDR followed by a sufficiently large number of randomizations guarantees a minimal accuracy ofπ/4[33,34].
3.2.2 The Power Allocation Between BS and UR
The power allocation between BS and UR must be determined by an iterative algorithm.Once the optimal phase shift is obtained,the total power allocation is then adjusted to increase the secrecy rate further.By substituting uH=andα=0.5 into(9)and(10),respectively,the optimization problem is translated into
OP4:
The objective function and the constraints are convex in OP4.can be solved effectively by the CVX.In addition,the initial value of the iteration point is set based on the equal power allocation standard.
3.2.3 The Power Allocation Between the Confidential Signal and the Jamming Signal Finally,the power allocation of the confidential signal and the jamming signal is processed.By substituting uH,into (9) and (10),the secrecy rate of the system is written as
By considering the monotonically increasing logarithm function,the power allocation problem of the confidential signal and the jamming signal is written as
OP5:
In brief,the maximal secrecy rate can be obtained by alternately optimizing variablesθ,PS,PRandαin an iterative way.The detailed process for solving problem OP1 is summarized in Algorithm 1.

3.2.4 Algorithm Analysis
(1) Computational complexity analysis: The main complexities are in executing Step 3 and Step 4,for which the worst-case complexities areOandO(I3.5),respectively,whereIpresents the number of optimization variables [21,35].The number of iterations required for the algorithm to reach convergence is assumed asr,the total complexity of Algorithm 1 is in the order ofO
(2) Convergence analysis: Algorithm 1 guarantees thatRsecis non-decreasing after each iteration.Moreover,if the total transmit power is limited,there exists an upper bound of the achievable secrecy rate.Thus,the convergence of the proposed Algorithm 1 is guaranteed.
IV.SIMULATION RESULTS
To evaluate the performance of the proposed scheme,Monte Carlo simulations are performed with 105independent experiments.Figure 2 shows that BS,UR,RIS,and D are located in the 3D space,and their coordinates are (0,0,0),(20,0,0),(20,5,5),and (40,0,0) respectively.To show the secrecy performance,four schemes are simulated,namely,the proposed optimal scheme for the RIS phase shift and the power allocation(JORP),a suboptimal scheme with the equal power allocation (SEPA),a suboptimal scheme with random phase shift(SRPS),and a scheme without an RIS (No-RIS).The RIS is equipped with 50 reflecting elements,the total transmit power is set asPT=40 dBm,the AWGN power is set asσ2=-10 dBm,the RSI power is set asγRR=-10 dBm,the path loss at the reference distance of 1 meter is set asρ=-30 dBm,the path-loss exponentkis set as 2.3,the maximal iteration numberrmaxis set as 10,and the Rician factorεis set as 10 dBm.

Figure 2.Model for simulation experiments.
Before evaluating the performance of the system,the convergence behavior of the iterative optimization algorithm is demonstrated by setting different total powers and numbers of reflecting elements.Figure 3 shows that the secrecy rate of the proposed JORP scheme gradually increases and stabilizes with the increase of the number of iterations.Moreover,for different transmission powers and numbers of elements,the algorithm converges after approximate five iterations.Therefore,the iterative algorithm has a fast convergence speed and low complexity.
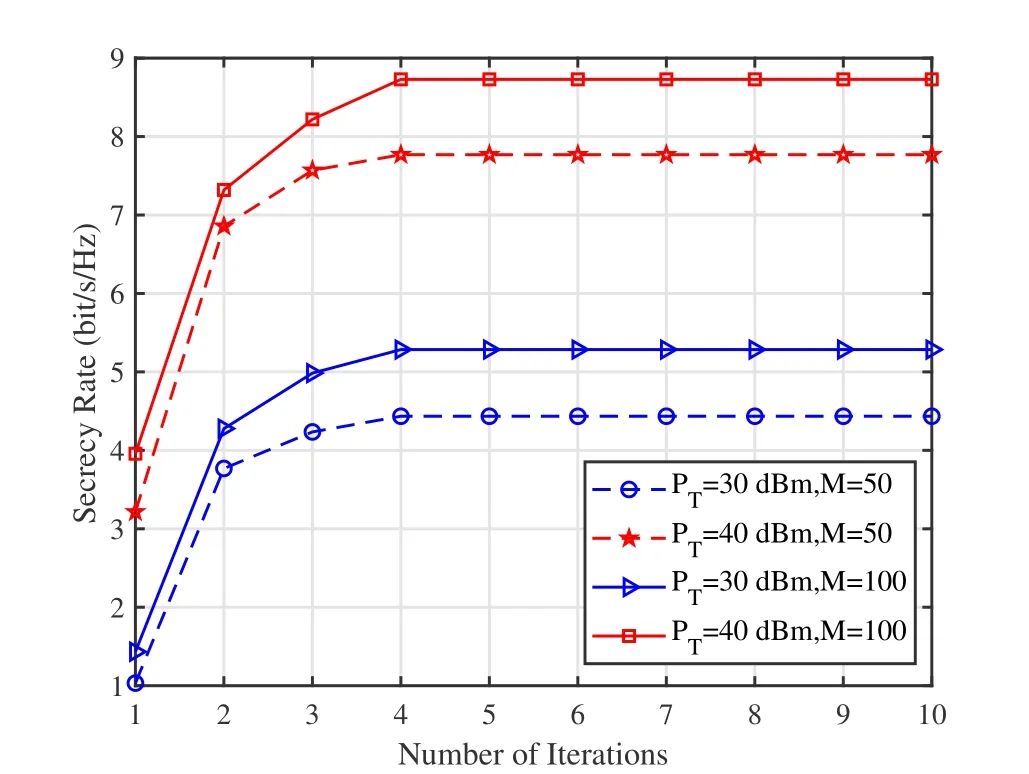
Figure 3.Secrecy rate versus iteration number.
Figure 4 demonstrates the effect of the total transmit power on secrecy rate.As transmit power increases,the secrecy rate gradually increases.Among all schemes with RIS,the proposed JORP scheme is the best in the whole power range,followed by the SEPA scheme,while the SRPS scheme performs worst.WhenPT=40 dBm,the proposed JORP scheme can achieve approximate 0.70 and 2.48 bit/s/Hz gain over SEPA and SRPS,respectively.As expected,the No-RIS scheme performs poorly due to the absence of RIS.Therefore,the scheme in the presence of RIS has a higher secrecy rate than the No-RIS scheme.In addition,deploying RIS in relay networks is efficient and feasible,since RIS is passive and does not require additional power consumption and radio frequency links.
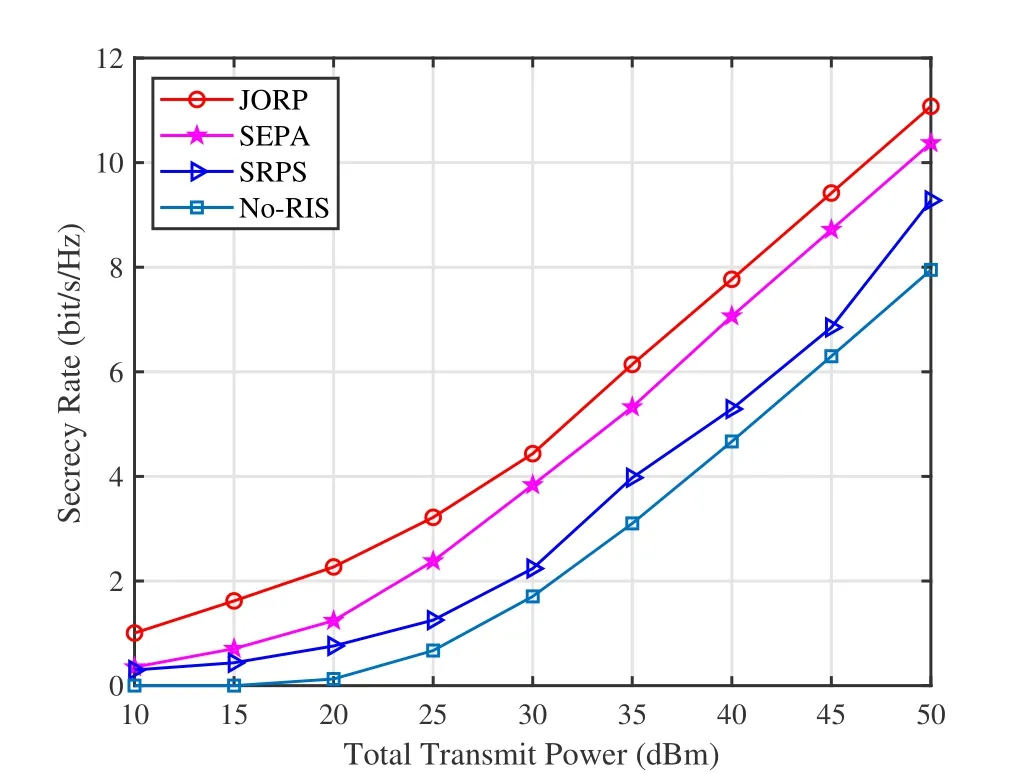
Figure 4.Secrecy rate versus total transmit power.
Figure 5 illustrates the relationships between the secrecy rate and the number of reflecting elements,which demonstrates that the proposed JORP scheme is remarkably superior to the other three schemes.The secrecy rates of the JORP and the SEPA schemes clearly increases withM,whereas the SRPS scheme only shows a slight improvement.It indicates that the received signal strength at the RIS increases,resulting in higher channel gain.The No-RIS scheme has a very low secrecy rate independent ofM.The performance of the JORP scheme is always better than the SEPA and the SRPS schemes.Hence,the joint design of the RIS phase shift and the power allocation can obtain optimal system performance.Furthermore,when the number of reflective elements is 50,the secrecy rate of the JORP scheme is increased by 3.10 bit/s/Hz compared with the No-RIS scheme.With the increase of reflective elements,the gap with the No-RIS scheme becomes increasingly substantial.In practice,system performance can be improved by increasing the number of reflective elements at the cost of hardware complexity.
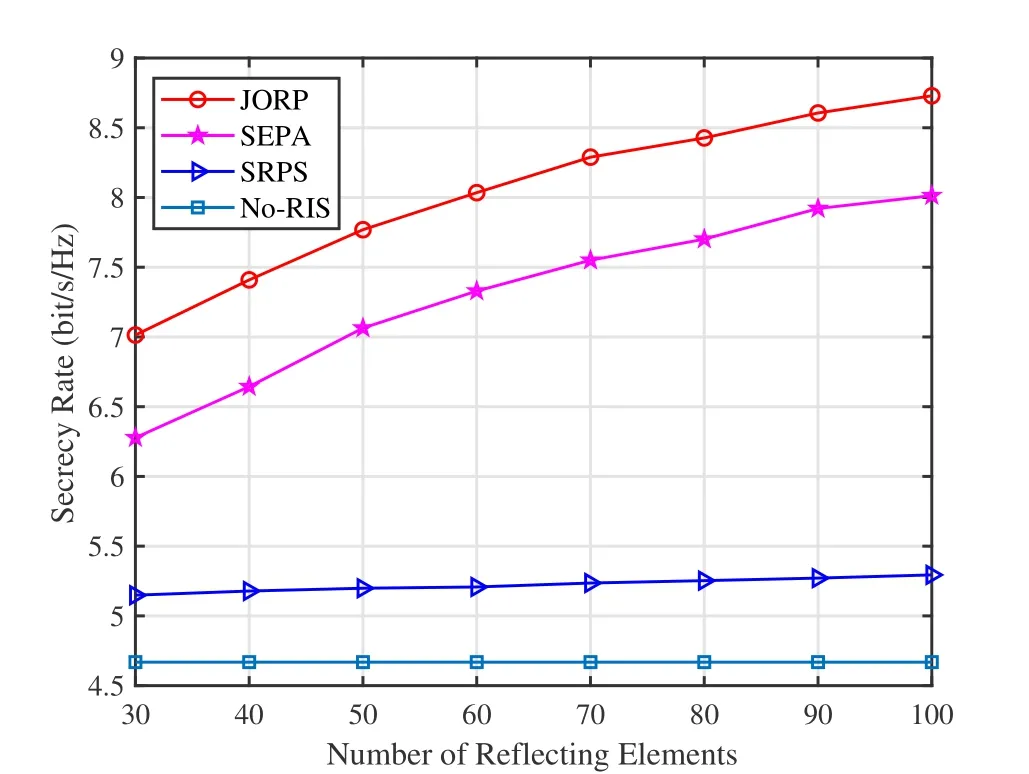
Figure 5.Secrecy rate versus the number of the reflective elements.
Figure 6 quantifies the effects of the location of the relay on the secrecy rate.An RIS is generally deployed on the building surface,while the relay can be flexibly deployed at any location in the cell.Therefore,the influence of relay location on secrecy rate is necessary to analyze.The UR is assumed arbitrarily deployed between BS and the D node.The secrecy rates of the four schemes first increase as the UR moves towards the center since the UR is untrusted.When the UR is located near the BS,more confidential signals are eavesdropped,which is not conducive to achieving a higher secrecy rate.However,as the UR moves to the D node,the secrecy rates of the JORP,SEPA,and SRPS schemes increase while that of the No-RIS scheme decreases.If the UR approaches the D node,RIS-assisted transmission is dominant,and the UR is difficult to steal information from the BS,increasing the secrecy rate.The secrecy performance of the No-RIS scheme gradually deteriorates as the UR moves to the D node due to the absence of RIS.
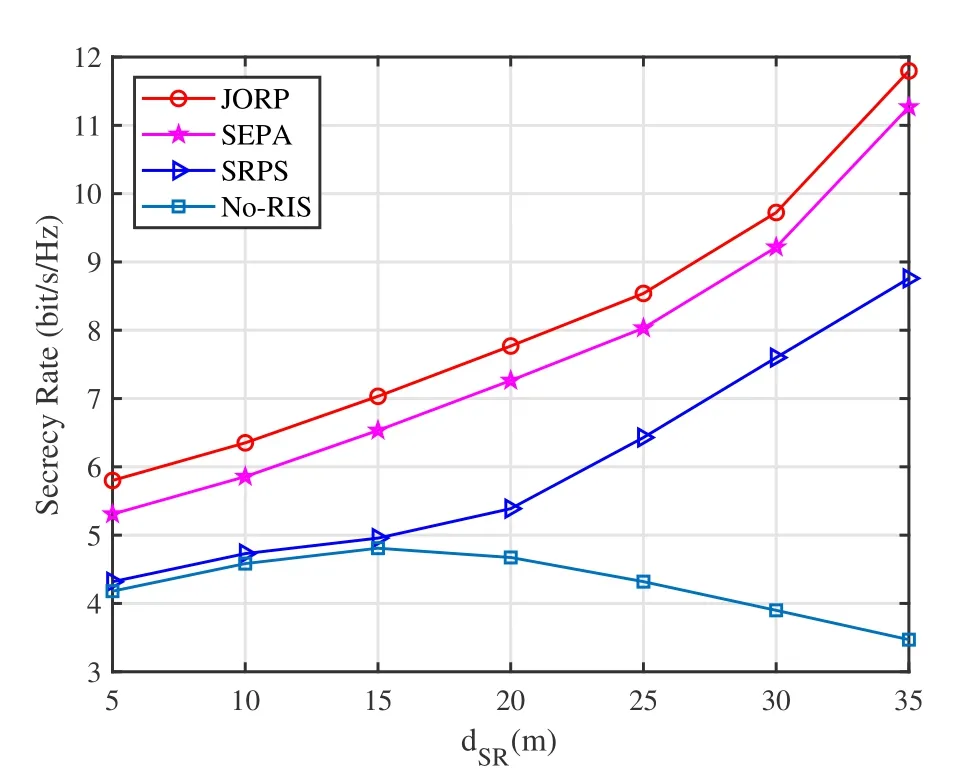
Figure 6.Secrecy rate versus the UR location.
V.CONCLUSION
This work aims to enhance the secrecy performance of the RIS-assisted UR networks by confusing the UR eavesdropping with the source-based jamming strategy.To maximize the secrecy rate,the RIS phase shift and the power allocation are optimized jointly under the constraints of unit modulus and total power.The best performance is achieved under different locations of the UR or the power allocation among the confidential signal,the jamming signal,the BS,and the UR.In addition,the effects of total transmit power,the number of reflective elements,and relay location on secrecy rate are analyzed.This work suggests that the proposed joint optimization scheme,which can switch among various scenarios flexibly,is always advantageous.The simulation results demonstrate that the iteration algorithm based on the SDR has a fast convergence speed.Moreover,compared with the benchmark scheme,the secrecy rate of the proposed scheme is always the best in various scenarios.
ACKNOWLEDGEMENT
This work is supported by the National Natural Science Foundation of China (Grant No.61961024),the Top Double 1000 Talent Programme of Jiangxi Province (Grant No.JXSQ2019201055),the Natural Science Foundation of Jiangxi Province (Grant No.20181BAB202001) and the Opening Project of Shanghai Key Laboratory of Integrated Administration Technologies for Information Security(Grant No.AGK201602).
杂志排行
China Communications的其它文章
- IoV and Blockchain-Enabled Driving Guidance Strategy in Complex Traffic Environment
- LDA-ID:An LDA-Based Framework for Real-Time Network Intrusion Detection
- A Privacy-Preserving Federated Learning Algorithm for Intelligent Inspection in Pumped Storage Power Station
- Secure Short-Packet Transmission in Uplink Massive MU-MIMO Assisted URLLC Under Imperfect CSI
- Multi-Source Underwater DOA Estimation Using PSO-BP Neural Network Based on High-Order Cumulant Optimization
- An Efficient Federated Learning Framework Deployed in Resource-Constrained IoV:User Selection and Learning Time Optimization Schemes
