An Efficient Federated Learning Framework Deployed in Resource-Constrained IoV:User Selection and Learning Time Optimization Schemes
2023-12-10QiangWangShaoyiXuRongtaoXuDongjiLi
Qiang Wang ,Shaoyi Xu,2,* ,Rongtao Xu ,Dongji Li
1 School of Electronics and Information Engineering,Beijing Jiaotong University,Beijing 100044,China
2 National Mobile Communications Research Laboratory,Southeast University,Nanjing 210096,China
Abstract: In this article,an efficient federated learning(FL)Framework in the Internet of Vehicles(IoV)is studied.In the considered model,vehicle users implement an FL algorithm by training their local FL models and sending their models to a base station(BS)that generates a global FL model through the model aggregation.Since each user owns data samples with diverse sizes and different quality,it is necessary for the BS to select the proper participating users to acquire a better global model.Meanwhile,considering the high computational overhead of existing selection methods based on the gradient,the lightweight user selection scheme based on the loss decay is proposed.Due to the limited wireless bandwidth,the BS needs to select an suitable subset of users to implement the FL algorithm.Moreover,the vehicle users’ computing resource that can be used for FL training is usually limited in the IoV when other multiple tasks are required to be executed.The local model training and model parameter transmission of FL will have significant effects on the latency of FL.To address this issue,the joint communication and computing optimization problem is formulated whose objective is to minimize the FL delay in the resource-constrained system.To solve the complex nonconvex problem,an algorithm based on the concave-convex procedure (CCCP) is proposed,which can achieve superior performance in the small-scale and delay-insensitive FL system.Due to the fact that the convergence rate of CCCP method is too slow in a large-scale FL system,this method is not suitable for delay-sensitive applications.To solve this issue,a block coordinate descent algorithm based on the one-step projected gradient method is proposed to decrease the complexity of the solution at the cost of light performance degrading.Simulations are conducted and numerical results show the good performance of the proposed methods.
Keywords: block coordinate descent;concave-convex procedure;federated learning;learning time;resource allocation
I.INTRODUCTION
With the rapid development of the Internet of Vehicles(IoV),machine learning has been widely applied to the IoV recently and plays a crucial role in automatic driving systems and vehicular resource management[1].In general,the present centralized machine learning method requires users to send all data to the cloud server and data center,which will bring large transmission delays and the risk of privacy leakage[2].Nevertheless,federated learning(FL),as a distributed machine learning method,has attracted much attention of many researchers[3].By using FL,the participants do not need to send the data they collected to the data center for training [4].They just leverage their own data to train local models respectively and then transmit their model parameters to the aggregation center,which can reduce the transmission load and protect the privacy of users effectively[5].
Despite the great prospect of the integrated FL and IoV system,there still exists a significant challenge.Generally,a successful FL requires a great number of iterations,and plenty of clients need to communicate with the central server to upload and update model parameters during every iteration[6,7].Frequent communications between vehicle users and the data center server not only require a higher transmission rate to ensure the validity of data but also generate lots of communication overhead.The extremely high transmission cost will become a bottleneck restricting the further development of FL.Therefore,under the requirements of high reliability and low latency of the IoV [8,9],it is necessary to focus on the latency reduction of FL considering energy consumption and explore the rational allocation of resources in the FL system.
To decrease the latency for FL,many researchers concentrated on the application of compression and sparsification techniques for deploying FL over wireless networks.They applied compression and sparsification for local ML model transmission to reduce the model transmission load and delay[10–13].However,the model’s compression and sparsification can only make transmission latency decrease.Actually,The training latency is also worth paying attention to if we desire to keep the whole learning time lower.Other works designed a novel FL framework with new training methods to execute FL efficiently[14–17].Nevertheless,they did not consider the problems brought by the resource-limited wireless network when FL is implemented,which is significant to reduce the latency of the whole FL system.
Based on the above observations,this paper proposes to decrease the communication cost and the delay of the FL system from two aspects,i.e.,a lightweight participating vehicle user selection and efficient resource allocation.Considering the difference of data samples between users,it is necessary for the base station (BS) to select the proper participating users to improve the accuracy of FL.Meanwhile,due to the high computational overhead of existing methods based on the gradient,the lightweight user selection scheme based on the loss decay is proposed.Due to the limited wireless bandwidth,the BS needs to select an appropriate subset of users to execute the FL algorithm.Besides,the vehicle users’ computing resource that can be used for FL is usually limited in the IoV when there are other multiple tasks required to be handled at the same time.The computing delay of local model training and the transmission delay of local model parameters will have significant effects on the latency of FL.Therefore,the joint communication and computing optimization problem is formulated whose objective is to minimize the FL delay in the resourceconstrained system.To solve the complex nonconvex problem,an algorithm based on the concave-convex procedure (CCCP) is proposed and has superior performance in the small-scale and delay-insensitive FL system.Due to the fact that the convergence rate of the CCCP method is too slow in the large-scale FL system,a low-complexity block coordinate descent algorithm based on the one-step projected gradient method is proposed to obtain the sub-optimal solution.
1.1 Related Work
Recently,some works focus on the application of FL in the vehicular network.[18] proposed an asynchronous federated deep Q-learning network-based task offloading (AF-DQN) algorithm to solve the task offloading subproblem by exploring the semidistributed learning framework.[19]proposed an optimal resource allocation approach based on FL in Edge Computing-Enabled Internet of Vehicles.[20] proposed a selective model aggregation approach,where fine local deep neural network(DNN)models are selected and sent to the central server by evaluating the local image quality and computation capability.In[21],a novel distributed approach based on FL is proposed to estimate the tail distribution of the queue lengths in vehicular communications.However,these existing works related to FL in IoV supposed that the FL system in their research was ideal and ignored the effect of latency as well as the energy consumption during the FL training and transmission.
Some works have studied the deployment problem of FL when it is used in wireless networks.[22]provided a novel framework for enabling the implementation of FL algorithms over wireless networks by jointly taking into account FL and wireless metrics and factors.[23] proposed an FL scheme considering the uncertainty of wireless channels and users with heterogeneous power constraints and local data size.A joint learning,wireless resource allocation,and user selection problem is formulated as an optimization problem whose goal is to minimize the FL convergence time and the FL training loss in[24].[25]proposed a control algorithm that determines the best tradeoff between local update and global parameter aggregation to minimize the loss function under a given resource budget.[26]proposed a joint learning and resource allocation scheme via optimizing transmit power of each device,time allocation,and user selection to reduce the FL transmission delay.[27] investigated the deployment of FL in an energy harvesting wireless network and proposed a joint energy management and user scheduling scheme.Nevertheless,most of these existing works[22–27]did not consider the allocation of computing power for participating users in consideration of users’ differentiation.How to allocate the limited computing resource is of great importance especially when multiple tasks are needed to be dealt with besides the FL task.In addition,[23] and [25]did not consider the FL participating user selection.In general,due to the limited wireless bandwidth resource,it is necessary to choose an appropriate part of users for the FL process.Although [24] proposed a gradient-based user association scheme,the calculation of all users’gradients will bring a large time cost,which is not proper for the latency-sensitive IoV scenario.
1.2 Contributions
To address the aforementioned problems,we investigate an efficient FL Framework in the IoV to decrease the communication cost and the delay of the FL system.The main contributions of this paper are concluded as follows:
1)Considering the scenario of the IoV,an FL framework based on participating user selection scheme with a low computational complexity is proposed.This scheme is different from many existing works which consider the gradient of the loss function with respect of model parameters.In terms of these methods,a great number of gradient calculations will incur large computing and time consumption.To solve this problem,an approximate alternative gradient calculation method is applied to acquire the loss function to reduce the cost of computation and time.Moreover,the participating vehicle selection scheme is described as a probability model,which means the opportunity of each user is determined by its contribution to the decay of the global loss function.
2) To study the learning time of the FL in the IoV,the transmission model,delay model,and energy consumption model for one FL iteration are illustrated in detail.Besides the consideration of communication resource allocation in many existing works,the vehicle users’ computing resource is also taken into account.In general,available computing resource can be used for FL is limited in the IoV when there are other multiple tasks required to be handled at the same time.And an optimization problem is formulated in our work whose objective is to minimize the delay during one FL iteration.
3) The joint resource block (RB),computing resource,and transmission power allocation schemes considering the resource-constrained FL system are proposed to solve the complex nonconvex optimization problem.To begin with,an efficient concaveconvex procedure (CCCP) algorithm is proposed to solve the complex mixed integer nonlinear programming problem which introduces a series of auxiliary variables to make the original optimization problem more tractable.Besides,the successive convex approximation (SCA) method is used to seek the solution to this nonconvex problem.This method can have superior performance in the small-scale scenario and is appropriate for delay-insensitive applications.
4)Considering the large-scale FL system,the algorithm convergence rate via the CCCP method will be too slow and undesirable.Hence,the low-complexity BCD algorithm based on the one-step projected gradient (PG) method is employed to alleviate the complexity of the solution,which is suitable for the delaysensitive applications in the IoV.The non-smooth objective in the original problem is transformed by introducing a smooth approximation method.And then,a block coordinate descent (BCD) method based on one-step PG is applied to the smoothed problem at the expense of light performance degrading.Simulations show that the proposed scheme can achieve a good performance which is close to CCCP method.
The remainder of this paper is organized as follows.In Section II,the system model and the learning time optimization problem formulation are presented.In Section III and Section IV,we design algorithms for the power allocation,computing and RB allocation.Simulation and results are described in Section V.Finally,the conclusion is provided in VI.
II.SYSTEM MODEL AND PROBLEM FORMULATION
In this section,an FL framework is firstly described in detail and the participating user selection scheme based on global loss decay is developed to reduce the latency of FL.And then the concrete models about transmission,delay and energy consumption are built.Finally,a delay optimization problem is formulated to design the FL algorithm over the wireless network.
2.1 Federated Learning Model
In our federated learning model,each vehicle user collects and preprocesses data by leveraging its own equipment.The data from the surrounding environment has the same type but different content.The number of vehicle users isUand the set of users is denoted asU={1,2,...,U}.Every vehicle users utilizes its data to train an FL local model and the base station aggregate all local models to get the global model.The global loss function is used to represent the global training effect and can be expressed as[28]
whereKdenotes the number of the whole data collected byUvehicles participating in training,Kirepresents the number of data samples collected by vehicle useri,the vectorgdenotes the global parameters,xikrepresents the sample input vector of vehicle useri,yikdenotes the true value andf(g,xik,yik)is a local loss function that captures the accuracy of the FL algorithm.It is noted that the specific definition of the loss function can be changeable for different learning tasks.
Actually,the target of local model training is to search the optimal model parameters by solving the following problem[28]
In general,the local model parameters are denoted asωiand the global modelgis calculated according to the following Federated Averaging (FedAvg) method[29]
Meanwhile,the gradient decent method is used to update the local modelωi,the updating process can be expressed as[30]
whereαdenotes the learning rate and∇f(gμ,xik,yik) represents the gradient off(gμ,xik,yik) with respect togμin theµth iteration.Therefore,BS and vehicle users can update their model based on (3) and (4),thereby solving the problem(2).
As shown in Figure 1,we consider a cellular network where one base station equipped with a center server covers multiple vehicle users.They jointly execute an FL algorithm for model training.The procedure of traditional FL is as follows
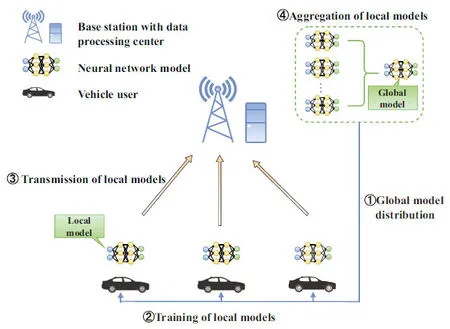
Figure 1.System model.
Step 1:The base station transmits the global model parameters to all vehicle users over the downlink.
Step 2:Each vehicle participating in the FL uses the data collected from the surrounding environment to update their models locally.
Step 3:The local model parameters will be sent to the base station for model aggregation over the uplink.
Step 4:The base station will integrate all local model parameters to update the global model parameters.
Step 5:Repeat Step 1-4 until the global model converges.
According to the training procedure above,we can see that the participating vehicles only need to share their local model parameters with the BS,which protects the privacy of vehicle users.However,as all model parameters are transmitted through wireless networks,the complex and changeable wireless transmission environment and the influence of the limited resource must be considered.
2.2 Participating User Selection for Federated Learning
In our research,in order to reduce the latency of FL,the participating user selection scheme based on the global loss decay is proposed.The global loss decay reflects the improvement of learning performance,which is given by
According to [27],there exists the relation between the global loss decay and the gradient of loss function which is given by
whereτis a coefficient determined by the specific neural network model and‖·‖2represents the L2 norm.During one iteration,BS tends to choose the users who can bring larger decreasing to the global loss function.
From(6),we observe that a great number of gradient operations are needed to acquire the loss decay,which will bring large computing consumption and time cost.Fortunately,according to [31],the gradient norm of the loss function for vehicle useri’s each data can be expressed as
Therefore,the loss decay of vehicle userican be evaluated by the square of its corresponding gradient norms,and can be written as
which represents the useri’s contribution to global loss decreasing.
To make the model training process converge faster,the proper participating user selection method should be considered.After users calculate their loss decay,they will transmit these values to the BS.Therefore,the selection bias for each user can be defined as
LetIμ,ibe the the probability selection model of vehicle useriand the thresholds of BS selection bias are denoted asTμ,1andTμ,2,(Tμ,1<Tμ,2).After the selection bias related to each user is derived from (9),Iμ,iis mapped into three levels according toTμ,1andTμ,2,and can be given by
wherelowpro,midproandhigproare three different selection probabilities.It should be noted that the values ofTμ,1andTμ,2will change with the FL process and vary from 0 to 1.
To calculate the selection bias in (9),the BS only needs to know Δfμ,i(gμ) of each useriwithout acquiring the exact data sample information.In fact,Δfμ,i(gμ)can be directly calculated by useriand each userionly requires to transmit a scalar Δfμ,i(gμ) to the BS.
2.3 Transmission Model
After the appropriate participating users are selected,their local models will be trained respectively.After that,these local models need to be sent to BS for model aggregation.Then the global model is updated and also required to be sent to vehicle users.Thus,the uplink and downlink transmission models need to be built.
We adopt the orthogonal frequency-division multiple access(OFDMA)to transmit the local FL models in an uplink way.The vehicle users connected to the same BS use the orthogonal frequency resource which is called a resource block (RB) in our paper.Since the vehicles under the coverage of different BSs use the same frequency resource,we must consider the interference between neighboring cells.Besides,we assume that the number of available RBs isRand each vehicle user can only occupy one RB.The uplink transmission rate of vehicle useriat iterationµcan be formulated as[32]
whererin,μis the RB allocation index indicator withrin,μ∈{0,1},rin,μ=1 means RBnis allocated to vehicle useri,andrin,μ=0,otherwise;pi,μdenotes the transmission power of vehicle useri;BUrepresents the bandwidth that each participating vehicle user occupies to send its local model parameters;hiis the channel gain between the useriand the BS;N0represents the noise power spectral density,andIndenotes the interference from neighboring cells due to reusing the same RBs.
Similarly,the downlink transmission rate of BS at iterationµcan be expressed as[32]
whereBDdenotes the bandwidth which the BS uses to broadcast the global model to useriandpBis the transmission power of the BS.
2.4 Delay Model
After the transmission model is developed,the delay model of FL during one iteration can be described further.
In our model,the delay of one FL iteration for each user consists of three main aspects: a) Local model training,b) Local model uploading,c) Global model distribution.LetDibe the size of useri’s training data in each communication round.The delay in regard to local model training of userican be expressed as
whereρis the number of central processing unit(CPU) cycles required for dealing with one bit data andfi,μrepresents the frequency of useri’s CPU.
In addition,according to (11) and (12),the uplink and downlink transmission delays between vehicleiand the BS are given by
whereO(ωi)is the data size of local model parameters which means the number of bits that vehicle users need to send to BS,andO(g) represents the data size of global model parameters that BS need to transmit to vehicle users.
Thus,the delay during one FL iteration is given by
whereLAis the delay for the BS to aggregate all local models.Due to the feature of model aggregation in the way of FedAvg method,this process only involves simple weighted summation,which needs less time consumption.Therefore,we can ignore the effect ofLAhere.
2.5 Energy Consumption Model
In our system model,we consider the energy consumption of vehicle users which consists of two aspects: a) Local model training,b) Local model uploading.Thus,the energy consumption of each userican be expressed as
2.6 Problem Formulation
To jointly design the wireless network and the FL algorithm,we now formulate an optimization problem whose goal is to minimize the delay during one FL iteration,while factoring in the wireless network parameters.This minimization problem includes optimizing transmit power allocation as well as resource allocation for each user.The minimization problem is given by
whereγTis the energy consumption of the FL algorithm andUrepresents the set size of participating vehicle users.(18a) and (18b) indicate that each uplink RB can only be allocated to one user.(18c)guarantees that each vehicle user can occupy one RB at most for uplink data transmission.(18d) ensures the energy consumption requirement of performing an FL algorithm at each learning step.(18e) constrains the maximum transmit power for each vehicle user.(18f)requires that the computing resource of each user is limited.From(18d)and(18e),we can see that the RB allocation matrixR,and the transmit power vectorPmust meet the power and energy consumption requirements during one learning iteration.
We observe that there are several challenges in P1.Specifically,the objective function is nonconvex and the user selection variableRis integral.In addition,the coupling constraints e.g.(18d)complicate the proposed problem further.Thus the problem P1 is a complex mixed integer nonlinear programming.Therefore,it is difficult to obtain the optimal solution to P1.
To address this problem in our work,two joint resource allocation schemes considering the wireless FL system are proposed.First of all,an efficient CCCPbased algorithm is proposed to solve the complex nonconvex optimization problem by introducing a series of auxiliary variables.In addition,the successive convex approximation (SCA) method is leveraged to seek the solution to this nonconvex problem.What’s more,in view of the complexity of CCCP method as the number of participating users grows,a lowcomplexity BCD algorithm based on the one-step PG method is proposed as well.The non-smooth objective in the original problem is transformed by introducing a smooth approximation method.And then a BCD method employing one-step PG is used to the smoothed problem.
III.PROPOSED CCCP-BASED ALGORITHM
In this section,to make the problem P1 become more tractable,a series of auxiliary variables are introduced,which guarantee the transformed problem to be equivalent to P1.Subsequently,an CCCP-based algorithm is proposed to solve the transformed problem.
3.1 Problem Transformation
Since the objective function of problem P1 is nonconvex,we introduce an auxiliary variableεto transform the original problem into an equivalent form.Furthermore,due to the existence of integer variablesR,we relax the binary variable into continuous form varies from 0 to 1,which means the BS’s association tendency for vehicle users.Specifically,BS expects to allocate RBnto vehicle useriwhenrinis close to 1.The transformed problem is given by
whereεrepresents the upper bound of the original objective function.
However,there still exist difficulties in designing the efficient algorithm for the problem P2 due to the variable coupling in constraints (18d) and (19b).To overcome this difficulty,a series of auxiliary variables{ξ,η,ν,χ}are introduced to deal with the constraint(18d),which is given by
and then the other variables{δ,φ,θ,φ}are employed to cope with constraint(19b),which can be expressed as
Therefore,the constraints (18d) and (19b) can be rewritten as a set of simpler constraints (20)-(29).Meanwhile,the problem P2 can be converted to P3
whereL={ξ,η,ν,χ,δ,φ,θ,φ}represents the set of auxiliary variables related to constraints (18d) and(19b).Since the problem P3 is equivalent to P2,they share the same global optimal solution under the given constraints.The detailed derivation of the equivalence between problems P2 and P3 is presented in Appendix A.Nevertheless,we can observe that the constraints(21),(22),(26),and(27)are still nonconvex.Thus,the difference-of-convex (DC) program is applied to our problem so that these nonconvex constraints can be approximated as more tractable convex expressions.
3.2 Proposed CCCP-Based Algorithm
As mentioned above,although the original problem has been transformed into a more tractable form,due to the nonconvexity and coupling of constraints it is still hard to solve the problem P3.To deal with this puzzle effectively,the concept of CCCP is leveraged to tackle the nonconvex constraints.We take an example for the operation of the constraint (21).First,the constraint(21)can be expressed as the form of DC and we have
where the first term and the second term are both convex functions.Then the subtracted convex terms in(31) is linearized by using the first-order Taylor expansion around thet-th iteration point(νt,ξt),we can approximate the constraint(21)as the following convex expression
Since other nonconvex constraints in problem P3 have a similar structure,the same approach can be applied to the rest constraints.Due to the space limitation,we omit specific derivations of them and provide the approximated convex constraints directly,which is shown in(33)-(35)for(22),(26)and(27)
Furthermore,the problem P3 can be reformulated as the approximated convex optimization problem in thet-th iteration
The problem P4 can be solved by the convex programming toolbox CVX [33] to obtain the next iteration point.The detailed implementation of the proposed algorithm is summarized in Algorithm 1.

3.3 Convergence Analysis and Computational Complexity
Eventually,the problem P4 will achieve a stationary solution through multiple iterations [34].The limit point derived by the proposed CCCP algorithm also satisfies the KKT conditions of the DC program and thus converges to a local optimal solution of problem P4,which can be proved by the similar method as in[35].
The overall computational complexity of Algorithm 1 is dominated by the interior point method implemented by CVX,which is determined by the number of required floating-point operations (FPOs) at each iteration.Therefore,the complexity of the proposed CCCP-based algorithm is given byO(I1U3.5)[36],whereI1denotes the number of required iterations andU3.5denotes the number of FPOs at each iteration.if the users’ numberUbecomes large,the complexity of this method will be too high to accept.
IV.PROPOSED BCD-BASED ALGORITHM
Although the CCCP-based algorithm can solve the original problem well in the small-scale and delayinsensitive scenario,the convergence rate will become too slow when the users’number becomes large.Thus,to solve this issue,we propose a low-complexity BCD algorithm based on the one-step PG method in this section so that the FL framework can be deployed for the delay-sensitive applications well in the large-scale scenario.In this algorithm,the non-smooth objective in the problem P1 is tackled by introducing a smooth approximation method.And then a BCD method based on one-step PG is applied to the smoothed problem.
4.1 Smooth Approximation of Objective Function
To address the problem of the non-differentiable objective function in the problem P1,we leverage the log-smooth method to approximate the objective function.Specifically,the well-known log-sum-exp inequality [37] is applied in our work and it is represented as
Thus,the problem P1 can be smoothly approximated as
whereβis the smooth approximation factor and
Asβbecomes larger,the log-sum-exp inequality is tighter.
4.2 Proposed BCD Algorithm
However,it is still difficult to solve the problem (38)directly due to the nonconvex constraints (18a) and(18d).To tackle the problem of nonconvexity and variable coupling,the binary relaxation and BCD method are used in our algorithm.In this method,each variable is updated sequentially while the other variables are fixed.For problem (38),the solving process is shown as follows:
1)LocalComputingResourceAllocation
First,we consider the subproblem of local computing resource allocation with fixingRandp,which is given by
where the whole constraints are convex.Hence,the one-step PG method [37] is used to solve problem(40).The variableFis updated according to the following formula
Since the objective function of (43) and constraint(18d) are the type of the convex quadratic function w.r.tthe closed-form solution for vehicle useriis formulated as
2)TransmissionPowerAllocation
Next,we consider the subproblem of transmission power allocation with fixingRandF,which is given by
However,the constraint (18d) is nonconvex,we can transform it into the convex form and we have

Now all constraints are convex which is similar to the problem(40).Therefore,the one-step PG method can be used to solve the problem (47).The variablePis updated according to the following formula
Since the optimization problem (51) is convex and satisfies the Salter’s condition,the dual gap is zero,i.e.,strong duality holds between (51) and its dual problem.Thus,the Lagrangian dual decomposition method[37]can be employed to obtain its optimal solutions.The Lagrangian function of(51)is given by
whereλ=(λ1,λ2,...,λU)≻0 is the dual variables corresponding to(52).Then,the dual problem can be expressed as
whereD(λ) is the Lagrangian dual function and can be expressed as
Given dual variablesλ,we can first obtain the optimal solution by using KKT conditions which is given by
And the optimal transmission power allocationis given by
To obtain the dual variables,we need to solve the maximization problem(53),a subgradient method can be utilized to update the dual variables which can be expressed as
3)VehicleUserRBAllocation
We consider the subproblem of RB allocation with fixingFandP,which is given by
Now,all constraints are convex when we relax binary variableRinto continuous form[0,1].Therefore,the one-step projected gradient method can be used to solve this problem (60).The variableRis updated according to the following formula
We can observe that the optimization objective is a convex quadratic function and all constraints are linear equations and inequations.Therefore,problem (63)is a standard convex optimization problem which can be solved by the interior point method well[38].The whole procedure of the proposed BCD method is summarized in Algorithm 3.
4.3 Convergence Analysis and Computational Complexity
Due to the fact that the limit point generated by Algorithm 3 is a stationary point of the smoothened problem (38),the algorithm can achieve convergence finally.The proof is similar to that of [39],and it is hence omitted as well.
Meanwhile,the computational complexity of Algorithm 3 can be assessed byO(N1(N2+N3)),whereN1denotes the number of iterations required by themain BCD loops in Algorithm 3,denotes the number of iterations required by Algorithm 2[40],anddenotes the number of iterations required by the interior point method [38].The value ofN2is mainly determined by the precision setting.In addition,N3will not become too large with the increase of users’number.Furthermore,it has been shown in[41]that the convergence rate of the PG method isO(1/N1).

From above description we can conclude that the PG-based BCD algorithm have less computational complexity than that of the CCCP-based algorithm in large-scale scenario.Accordingly,the PG-based BCD algorithm will be more suitable for a large-scale and delay-sensitive FL system in IoV.
V.SIMULATION RESULTS
5.1 Simulation Parameters Setting
In our research,a circular network area with a radiusr=500 m is considered where one BS is located at its center servicing 20 vehicle users.The value of intercell interference is randomly selected and varies from-10 dBm to 20 dBm.We leverage the MNIST dataset to train our FL models generated based on Tensorflow deep learning framework.The neural network consists of convolutional layers,pooling layers and fully connected layers whose structure is described in Figure 2.In addition,our dataset is composed of 2800 handwritten digits.Besides,the thresholds of BS selection biasTμ,2andTμ,1correspond to theRth and theUth highest bias value in theµth FL round.Ris the number of available RBs.AndUrepresents the number of the participating users to be selected.The other major simulation parameters are shown in Table 1.

Table 1.System parameters.
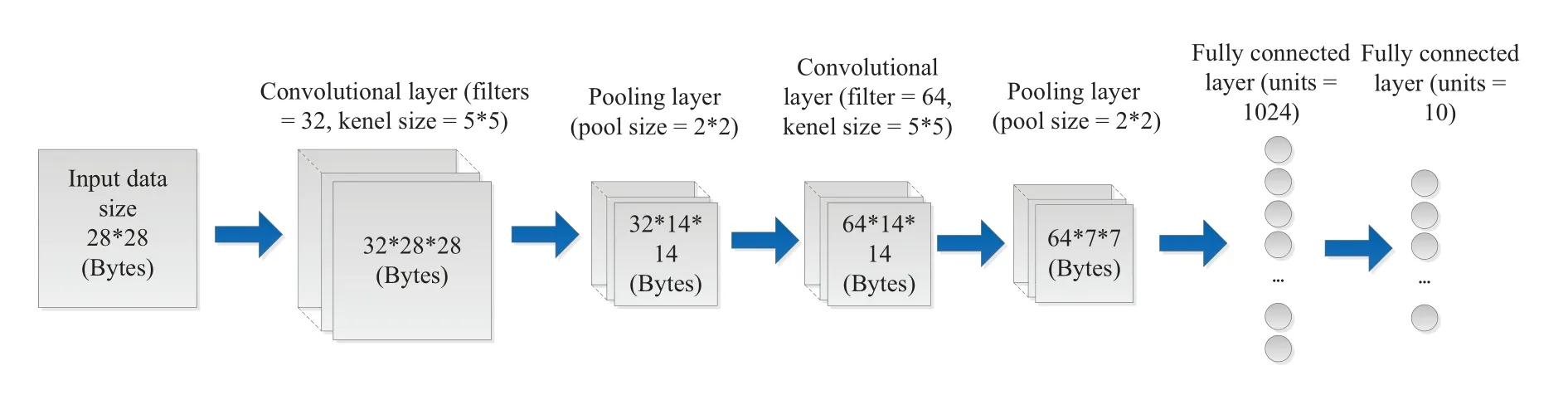
Figure 2.Data size changes under neural network structure we used.
For comparison purposes,four baselines are selected in our simulation:
a)CV-PG:An FL algorithm that uses the proposed method but randomly determines user transmission power allocation.
b) PV-PG: An FL algorithm that uses the proposed method but randomly determines user computing resource allocation.
c)MAX-C:An FL algorithm that uses an allocation scheme of maximizing computing resources.
d)CP-PG:An FL algorithm that uses random vehicle user selection.
5.2 Performance Evaluation of Proposed Algorithms
To evaluate the learning time of the proposed joint computing resource,transmission power,and vehicle user selection method based on PG (CPV-PG) and CCCP,we compare the performance of the proposed method with CV-PG,PV-PG and CP-PG.In Figure 3,we first find that the learning time gradually increases as the number of available RBs becomes larger for these six schemes.Secondly,we observe that the proposed CCCP scheme and CPV-PG scheme withβ=101have similar performance in terms of latency reduction and outperform other four schemes.Besides,the performance of CCCP scheme is slightly better than that of CPV-PG scheme withβ=101in the two cases of the different maximum power constrains.On the whole,the two schemes have similar performance in both cases when compared with other schemes.With regard to the first phenomenon,that’s because when the selected participating vehicle users become more,the system needs to take all users’ FL process into consideration at the same time,which makes the time of one iteration become longer.As for the second phenomenon,on the one hand,this attributes to the fact that the proposed schemes apply joint vehicle user selection,computing resource and transmission power allocation to the FL algorithm.Since the proper user with great contribution are selected in the FL training process and resources are reasonably allocated,which makes model learning become faster.On the other hand,this is because the original optimization objective is properly approximated in the CPV-PG scheme whenβ=101,which results in a great performance close to the CCCP scheme.In addition,we can find that the results are not satisfying if the smoothness factor is too large for CPV-PG method.

Figure 3.Learning time versus the number of available RBs.
To study the energy consumption of our proposed method further,as the number of available RBs varies the changes of the system energy consumption for six methods are shown in Figure 4.First,we can see that our proposed CCCP scheme and CPV-PG scheme withβ=101has an advantage over CV-PG,CP-PG scheme and CPV-PG scheme withβ=103.Besides,the gap between our proposed methods(CPV-PG withβ=101and CCCP) and other methods becomes wider as the number of available RBs becomes larger.Second,we observe that the energy consumption of CPV-PG withβ=101is fairly close to that of MAXC.Third,the performance of CCCP scheme is slightly better than that of CPV-PG scheme withβ=101in the two cases of the different maximum power constrains.On the whole,when compared with other schemes,the two schemes have similar performance in the aspect of the energy consumption in both cases.For the first phenomenon,it is due to the fact that CVPG determines user transmission power in a random way and CP-PG ignores users with lower energy consumption.Besides,the proposed CCCP scheme and CPV-PG scheme withβ=101jointly introduces vehicle user selection,computing resource and transmission power allocation to resource-constrained FL system,which can decrease the energy consumption effectively especially when the number of selected participating vehicle users increases.The second phenomenon illustrates that in order to decrease the delay of the FL system,the CPV-PG method withβ=101actually leverages the maximum computing resource allocation under the condition of meeting the energy consumption constraint.In addition,the third phenomenon illustrates that the CPV-PG method withβ=101also owns great performance in the reduction of energy consumption as the smooth approximation function is suitable for our original problem.However,when the smoothness factor is too large for CPVPG method,it is difficult to acquire satisfying results.
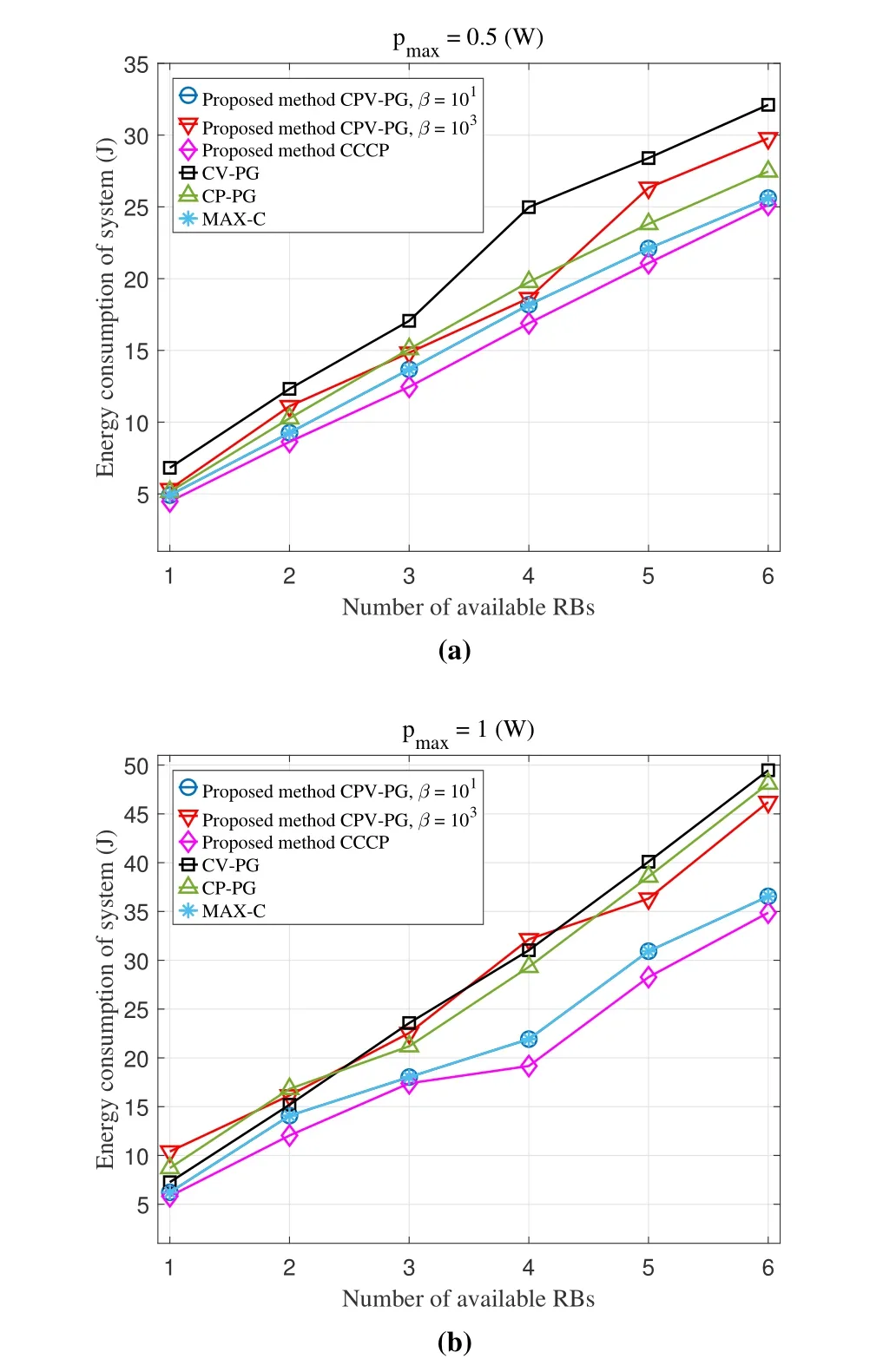
Figure 4.Energy consumption versus the number of available RBs.
To further explore the convergence performance of three FL algorithms which employ CPV-PG,CCCP and CP-PG respectively,Figure 5 illustrates how the identification accuracy and the value of loss function change as the number of iterations varies in the test dataset.Firstly,we can see that all three FL algorithms can converge when the number of iterations reaches about 10.In addition,the performance of the three methods under condition of 6 available RBs is better than that of them under condition one available RB.Secondly,we can observe that the identification accuracy of FL algorithms based on CCCP and CPV-PG is over 95%when the number of available RBs is 6.Besides,the value of their loss function is less than 0.2 in the same case.However,the identification accuracy of FL algorithms based on CP-PG is always below 90%and the value of the loss function is higher than the proposed two methods when the number of available RBs are 1 and 6.The first phenomenon describes that all three different FL methods have good convergence performance.And due to the increase of participating users’ number,the system can take advantage of more users’information,which will improve the performance of FL system.The main reason for the second phenomenon is that the FL scheme based on CPVPG and CCCP both utilize the proposed participating user selection and RB allocation method,which can effectively select users who have more contributions to the learning accuracy improvement and the training loss reduction.
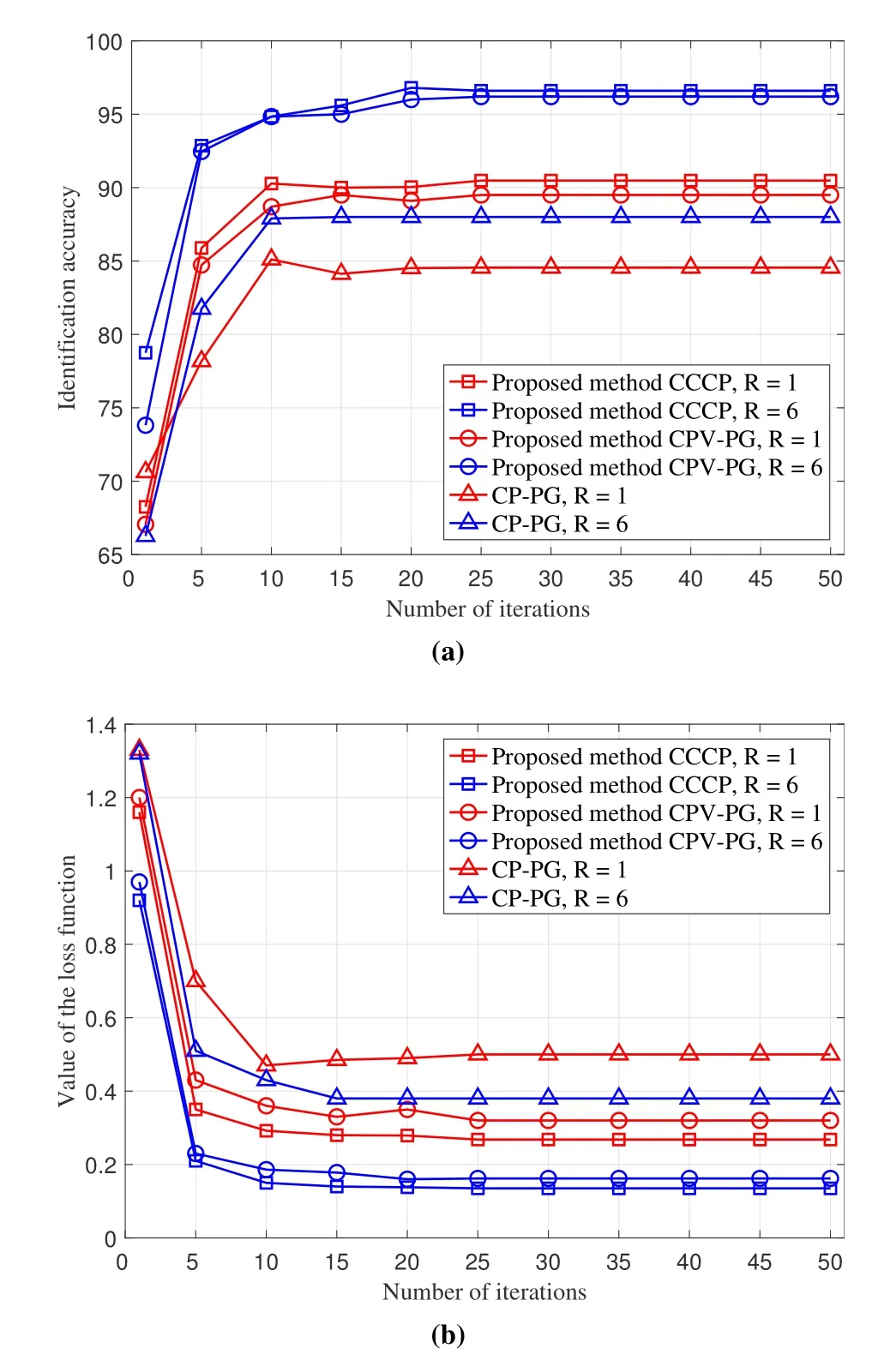
Figure 5.(a)Identification accuracy versus the number of iterations. (b) Testing loss changes versus the number of iterations.
5.3 Performance Evaluation of Proposed User Selection Scheme
To verify the effect of the proposed participating user selection scheme with a low computational complexity,we compare the performance of the FL algorithms which employ CPV-PG and CP-PG in terms of identification accuracy and the value of loss function as the number of epochs and available RBs changes.The numerical simulation results are shown in Figure 6 and Figure 7.
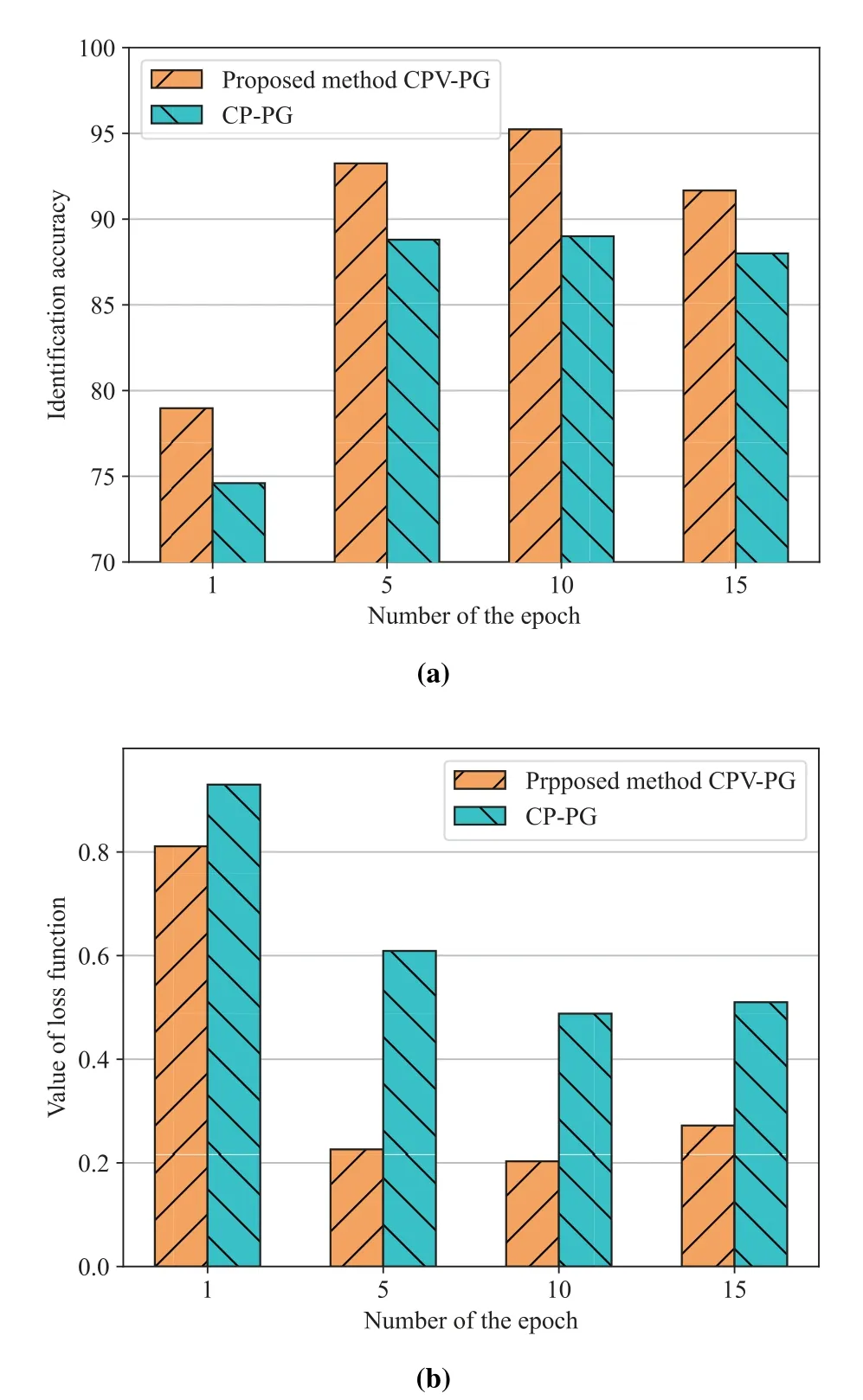
Figure 6.(a)Identification accuracy versus the number of the epoch.(b)Testing loss changes versus the number of the epoch. (The number of RBs is 4)
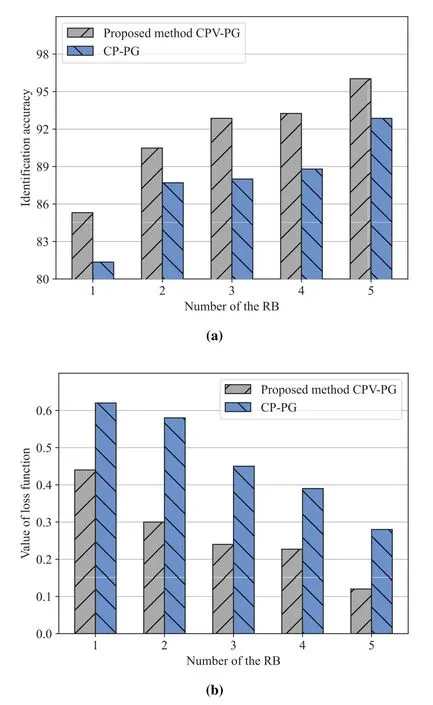
Figure 7.(a) Identification accuracy changes versus the number of available RBs. (b) Testing loss changes versus the number of available RBs. (The number of the epoch is 5)
From Figure 6(a)and Figure 6(b),we can first find that the FL algorithm using the CPV-PG method always outperforms the FL algorithm based on CP-PG in the two aspects we mentioned before.Second,we observe that the performance of the two methods will not be improved all the time with the increase of the epochs’number in the FL local training process.Especially when the number of epochs reaches 15,the decrease in identification accuracy occurs.Specifically,the identification accuracy of FL algorithms based on CPV-PG and CP-PG is decreased by 3.57% and 1%respectively.And the values of their loss function are increased by 0.69 and 0.22 respectively.For the first phenomenon,it is due to the fact that the FL scheme based on CPV-PG can select vehicle users with the proposed participating user selection to effectively improve the learning accuracy.In addition,the second phenomenon illustrates that we need to determine the appropriate training epoch in practice for FL algorithms based on CPV-PG and CP-PG to guarantee the best performance.
In Figure 7(a) and Figure 7(b),we firstly find that the FL algorithm using the CPV-PG method has better performance than the FL algorithm based on CPPG all the time.In addition,we see that the performance of the two methods is gradually improved with the growth of available RBs’ number during the process of FL local training.To be specific,the identification accuracy of FL algorithms based on CPVPG and CP-PG is increased to 96.03% and 92.86%respectively.Moreover,the values of the loss function related to these two algorithms are dropped by 0.12 and 0.28 respectively.With regard to the first phenomenon,that’s because the random user selection scheme of the CP-PG scheme does not consider different users’ contributions,which will have an adverse influence on model learning.As for the second phenomenon,this attributes to the fact that the FL system can take advantage of more useful data during the training process with more participating vehicle users,which will improve the performance of the neural network.
5.4 Complexity Evaluation of Proposed Algorithms
As mentioned above,the performance of the FL algorithm based on CPV-PG is similar to that of the FL algorithm based on CCCP in terms of learning time,energy consumption and convergence.What’s more,to verify the complexity of two proposed joint computing and transmission resource allocation methods further,the complexity analysis of the proposed two algorithms is shown in Figure 8(a).For the CCCPbased algorithm,the value of the objective function for (18) versus the iteration number is plotted.With regard to the CPV-PG algorithm,the values of the objective function for (18) and (38) with the variation of the iteration number are plotted.We can observe that the CPV-PG algorithm can achieve faster convergence than the CCCP algorithm.In addition,since the CCCP-based algorithm needs to deal with a complex convex problem during one outer iteration,a single iteration of BCD will consume much less time than the corresponding CCCP iteration,which can be explained well by the average execution time in Figure 8(b).To sum up,due to the great performance close to CCCP method but lower complexity,the CPV-PG algorithm is more efficient than the CCCP-based algorithm in the large-scale and delay-sensitive scenario of the IoV.
VI.CONCLUSION
In this paper,a novel framework that enables the implementation of FL algorithms over wireless networks is developed.The learning time problem of federated learning in an IoV is studied.First,a low computational complexity participating user selection scheme is proposed to reduce the FL learning time.Then,RB allocation,computing resources and power allocation are taken into consideration for a complicated optimization problem whose objective is to minimize the FL delay during one iteration.To solve the complex nonconvex optimization problem,the CCCP-based algorithm is proposed by introducing a series of auxiliary variables.Besides,the SCA method is also used to tackle the nonconvex constraints.Due to the fact that the convergence rate of CCCP method is too slow in large-scale FL system.To decrease the complexity of solution,a low-complexity BCD algorithm based on the one-step PG method is proposed.In this algorithm,a smooth approximation method is introduced to tackle the original problem.And then a PG-based BCD method is applied to the smoothed problem.Simulations show that the two proposed schemes both have close performance in terms of learning time and energy consumption for the wireless FL system in the IoV.Moreover,numerical results verify the low complexity and high efficiency of proposed BCD method.To sum up,the BCD algorithm is more efficient than the CCCP-based algorithm in the large-scale scenario of the IoV due to the great performance close to CCCP method but lower complexity.Therefore,the BCD algorithm is more appropriate for delay-sensitive networks.Besides,CCCP method is more suitable to be leveraged to obtain a better solution in the small-scale scenario and delay-insensitive networks.Due to the space limitation,there have been various important issues that have not been addressed in this paper.The efficiency optimization of hierarchical FL will be studied in our future work.
ACKNOWLEDGEMENT
This work was supported by the Fundamental Research Funds for the Central Universities(No.2022YJS127),the National Key Research and Development Program under Grant 2022YFB3303702 and the Key Program of National Natural Science Foundation of China under Grant 61931001.
APPENDIX
A Proof of Equivalent Transformation
First,we focus on the constraint(18d)in problem P2.In order to convert the constraint (18d) to a simpler one,a set of auxiliary variables{ξ,η,ν,χ}is introduced.The specific manipulations for the constraint(18d)is expressed as
The auxiliary variableξirepresents the lower bound ofηi/νiand can be represented as
Therefore,we obtain the constraints(20)-(24).
Similarly,we introduce the auxiliary variables{δ,φ,θ,φ}to transform (19b) into a tractable one,which can be described as
The auxiliary variableφiis defined as the upper bound ofθi/φiwhich means
And the auxiliary variableδiis defined as the upper bound of 1/fiand can be expressed as
Thus,the constraints (25)-(29) is obtained.Finally,the complicated constrains (18d) and (19b) in the problem P2 are substituted with (20)-(29) so that we obtain the equivalent problem P3.
B Proof of the Subgradient
From the definition ofD(λ),we have
where the inequality holds sinceis the optimal solution corresponding toλ.Rearranging the formula above yields
杂志排行
China Communications的其它文章
- Multi-Source Underwater DOA Estimation Using PSO-BP Neural Network Based on High-Order Cumulant Optimization
- Multi-Objective Optimization for NOMA-Based Mobile Edge Computing Offloading by Maximizing System Utility
- LDA-ID:An LDA-Based Framework for Real-Time Network Intrusion Detection
- A Privacy-Preserving Federated Learning Algorithm for Intelligent Inspection in Pumped Storage Power Station
- Secure Short-Packet Transmission in Uplink Massive MU-MIMO Assisted URLLC Under Imperfect CSI
- ELM-Based Impact Analysis of Meteorological Parameters on the Radio Transmission of X-Band over the Qiongzhou Strait of China
