Multi-Source Underwater DOA Estimation Using PSO-BP Neural Network Based on High-Order Cumulant Optimization
2023-12-10HaihuaChenJingyaoZhangBinJiangXuerongCuiRongrongZhouYuchengZhang
Haihua Chen ,Jingyao Zhang,* ,Bin Jiang ,Xuerong Cui ,Rongrong Zhou ,Yucheng Zhang
1 Institute of Computing Technology,Chinese Academy of Sciences,Beijing 100080,China
2 College of Oceanography and Space Informatics,China University of Petroleum(East China),Qingdao 266580,China
3 China YITUO Group Co.,Ltd,Luoyang 471000,China
Abstract: Due to the complex and changeable environment under water,the performance of traditional DOA estimation algorithms based on mathematical model,such as MUSIC,ESPRIT,etc.,degrades greatly or even some mistakes can be made because of the mismatch between algorithm model and actual environment model.In addition,the neural network has the ability of generalization and mapping,it can consider the noise,transmission channel inconsistency and other factors of the objective environment.Therefore,this paper utilizes Back Propagation(BP)neural network as the basic framework of underwater DOA estimation.Furthermore,in order to improve the performance of DOA estimation of BP neural network,the following three improvements are proposed.(1)Aiming at the problem that the weight and threshold of traditional BP neural network converge slowly and easily fall into the local optimal value in the iterative process,PSO-BP-NN based on optimized particle swarm optimization(PSO)algorithm is proposed.(2) The Higher-order cumulant of the received signal is utilized to establish the training model.(3) A BP neural network training method for arbitrary number of sources is proposed.Finally,the effectiveness of the proposed algorithm is proved by comparing with the state-of-the-art algorithms and MUSIC algorithm.
Keywords: gaussian colored noise;higher-order cumulant;multiple sources;particle swarm optimization(PSO)algorithm;PSO-BP neural network
I.INTRODUCTION
Direction of Arrival (DOA) [1–5] estimation is to process multiple signal sources received by a passive sensor array,so as to obtain direction information of multiple targets.DOA estimation is one of the most basic problems in sonar,radar,and mobile communications[6–10].
Generally,the DOA estimation algorithms can be divided into two categories.The first one is the algorithms based on mathematical model,such as Multiple Signal Classi-fication (MUSIC) [11,12],Estimation of Signal Parametersvia Rotational Invariance Techniques (ESPRIT) [13],Maximum Likelihood (ML)[14–16]and Weighted Subspace Fitting(WSF)[17].
These algorithms have a common characteristic,that is,it needs to match the algorithm model with the objective real environment model in order to obtain better DOA estimation performance.However,in practical environment,such as underwater DOA estimation,it is difficult to establish accurate models of channel,noise,signal and other factors.
The second kind of algorithm is based on machine learning,such as Neural Networks (NNs) [18].The neural network has the characteristics of nonlinear mapping and generalization.In the actual DOA estimation,such factros as signal-to-noise ratio,coherence of signals,transmission channel inconsistency,etc,can be considered into neutral network.In addition,in the process of neural network operation,it is only necessary to input test samples into the input layer of neural network to achieve the purpose of DOA estimation.
There are many types of neural networks,and the reference[19]and[20]introduce the utilize of Radial Basis Function Neural Network (RBF-NN) for DOA estimation.Although the DOA accuracy of RBFNN is high,the computational complexity is also extremely high.With the development of RBF neural network,A.H.El zooghby[21]and others put forward a method that it can utilize linear array to track fixed number of sources with arbitrary angle interval.
The literature[22]employs Support Vector Regression (SVR) to improve the DOA resolution,while SVR is a small sample set learning method with a solid theoretical foundation and limits its application in practice.In addition,[23] utilizes a Multilayer Perceptron(MLP)neural network to enhance the non-linear interpretation ability to the DOA mapping model.In [24],MLP neural networks are adopted to estimate possible sub-areas,and RBF neural networks are utilized for fine position estimation.However,as the number of MLP network layers increases,the generalization performance may not necessarily be improved,which means that the accuracy of DOA estimation is insufficient.
In terms of generalization performance,Deep Learning (DL) has made significant progress [25–27],and the generalization performance is further improved as the training set increases.Various methods for DOA estimation based on deep learning have been proposed.In [28],an autoencoder network and multiple small parallel classifier networks are cascaded to achieve DOA estimation.This hierarchical Deep Neural Network (DNN) framework effectively reduces the complexity of classifiers with the autoencoder network while this method requires the known number of sources.Using the sparse prior,[29–32]formulate multi-source DOA estimation as a multilabel multi-classification problem by Convolutional Neural Networks(CNNs)[29,30]and Convolutionalrecurrent Neural Networks (CRNNs) [31,32],respectively,while the accuracy depends on the number of grids.Generally,existing DL-based methods formulate DOA estimation as a multi-label multiclassification problem.However,the accuracy of these methods is limited by the number of grids,and the performance is overly dependent on the training data set.When the grid is densely divided,the real-time performance of DOA estimation is difficult to be guaranteed.
As the structure of the neural network for DOA estimation becomes more and more complex,the accuracy of DOA estimation is gradually improved.However,with the complexity of the structure,the related computational complexity is also increasing,which seriously affects the real-time performance of DOA estimation.Therefore,this paper takes BP-NN as the framework for further research.However,there are three defects of BP-NN.
First,the convergence method of weight and threshold factors of BP-NN adopts gradient descent method,which is prone to fall into the local optimum and keep the DOA estimation error larger.The group heuristic algorithm Particle Swarm Optimization(PSO)[33–35] algorithm not only has fast convergence rate,but also can achieve global optimum.Therefore,this paper proposes a PSO-BP-NN algorithm.
Second,in the trainning process of the tranditional neural network,it usually assumes that the noise of the received signal is Gaussian white noise.However,in the actual underwater environment,the noise can be variable,such as Gaussian colored noise.High-order cumulant [36–38] usually have insensitivity to various Gaussian processes and possess excellent properties in mathematical expressions.The influence of Gaussian colored noise on DOA estimation can be effectively suppressed by utilizing High-order cumulant.Therefore,this paper proposes a neural network training method based on the High-order cumulant of received data to reduce the impact of variable noise on the overall performance of the system.
Third,the traditional neural network algorithm often assumes that there is only one or two signal sources,but this is obviously not consistent with the actual situation.Therefore,this paper proposes a DOA estimation algorithm for the number of arbitrary sources based on optimized neural network.Finally,the simulation in Section V shows that the improved algorithm has higher accuracy and universality in DOA estimation.
The remaining sections are as follows.The Section II introduces array signal model.The Section III introduces the optimization algorithm model.In Section IV,a variety of BP neural network optimization algorithms are proposed.The Section V is the simulation results.The Section VI is the conclusion.
II.ANTENNA ARRAY MODEL
Suppose that the number of array elements isp.In theory,the array manifold is arbitrary.However,in the actual DOA estimation,the array model is usually set as special array configuration,such as Circular Array,Uniform Linear Array(ULA),etc.
In addition,it is assumed that there areqfar-field narrow-band signals impinging on the sensor array from distinct directionθ1,θ2,...,θqrelative to the reference point,and the center frequency of these signals is known.
Note that due to the influence of multi-path propagation,the received signal may be coherent.Due to the correlation signal is non independent,the number of independent sources of receiving array signal is less thanq.It is also noteworthy that the signal assumed in this model is a narrow-band signal andp>q.
Assuming that the array elements are not mutually coupled and the phase of the array elements are inconsistent,the received signalsl(t)can be expressed as
In equation (1),ul(t),φ(t),w0are the amplitude,phase,and frequency of the signal received by the array.The far-field narrow-band signal has the following expressions
From equation(1)and equation(2),we can get
It can be seen that the received signal of the kth array element is
In equation (4),ak(θ)is the amplitude response of the kth sensor to the wave-front impinging from the directionθ.nk(t)is the noise of the kth array element at timet.τk(θ)is the delay between the reference array element and the kth array element.
Assuming that the array elements are isotropic and independent.Using complex envelope representation,equation(4)can be expressed as
Wheresl(t) is the lth signal received at a certain timet.n(t) is the noise vector.a(θ) is the “steering vector” of the array towards directionθ,which is presented as
Where,w0=2πf=c is the speed of light.The superscriptTdenotes the transpose of a matrix.
In the matrix notation,equation(5)can be expressed as
Assuming that the data receiving matrix x(t)is sampled at timet1,t2,...,tNto form the sampling matrix X.
The covariance matrix R of array received data is
In the above formula,fis the signal frequency andλrepresents wavelength.RSand RNrepresent the covariance matrix of signal and noise,respectively.
The problem of DOA estimation is described as follows.Given the sampled data X,a set of estimated directions can be obtained
ofθ1,θ2,...,θq.
III.BP NEURAL NETWORK
BP-NN has the characteristics of nonlinear mapping and generalization.In the actual DOA estimation,the neural network can consider factors such as signal-tonoise ratio,coherence,transmission channel inconsistency,etc.,which has excellent robustness.Therefore,this paper takes BP-NN as the framework for further research.
3.1 The Principle of BP Neural Network
BP algorithm model mainly includes two aspects: forward received signal information transmission and backward error information transmission.In DOA estimation,the normalized data signal received by the array is input through the input layer of BP-NN,and output from the hidden layer through the optimization of weights and thresholds.Finally,outputting the results to the output layer.The actual output value will be compared with the ideal output value.If it is larger than the set error range,it will enter the reverse error propagation stage.The error information will pass through the output layer to the hidden layer,and then to the input layer.In the process of the reverse error propagation stage,the weights and thresholds are adjusted by neural network.Finally,the output value of BP-NN is close to the ideal output value by repeating the above two processes.The process of updating weights and thresholds in neural network according to the output error is the training process of neural network.
The principle of BP-NN algorithm is as follows.
Step 1: Initialize the parameters of neural network,such as weightwi,thresholdbi,minimum error valueε,ect.
Step 2: Define the input informationx=(x1,x2,...,xn)Tand expected outputting valuey=(y1,y2,...,yn)of neural network.
1.The outputting valueujof neurons in the hidden layer and output layer was calculated by forward propagation method:
2.Calculating the errorδjof each hidden layer neuron by back propagation:
Among them,δiis the sum of all the neuron error information of layerj+1.
3.Correction weight coefficient:
4.Updating the weight coefficient of the neuron:
Step 3: Training samples are input and the second step should be repeated until the error between all the output values and the expected value is less thanε,or the learning times reach the set maximum value.
The BP-NN model is a multi-layer forward neural network model,which can effectively solve the connection weight coefficients between hidden neurons in the network.The structure of BP-NN is shown in the Figure 1.
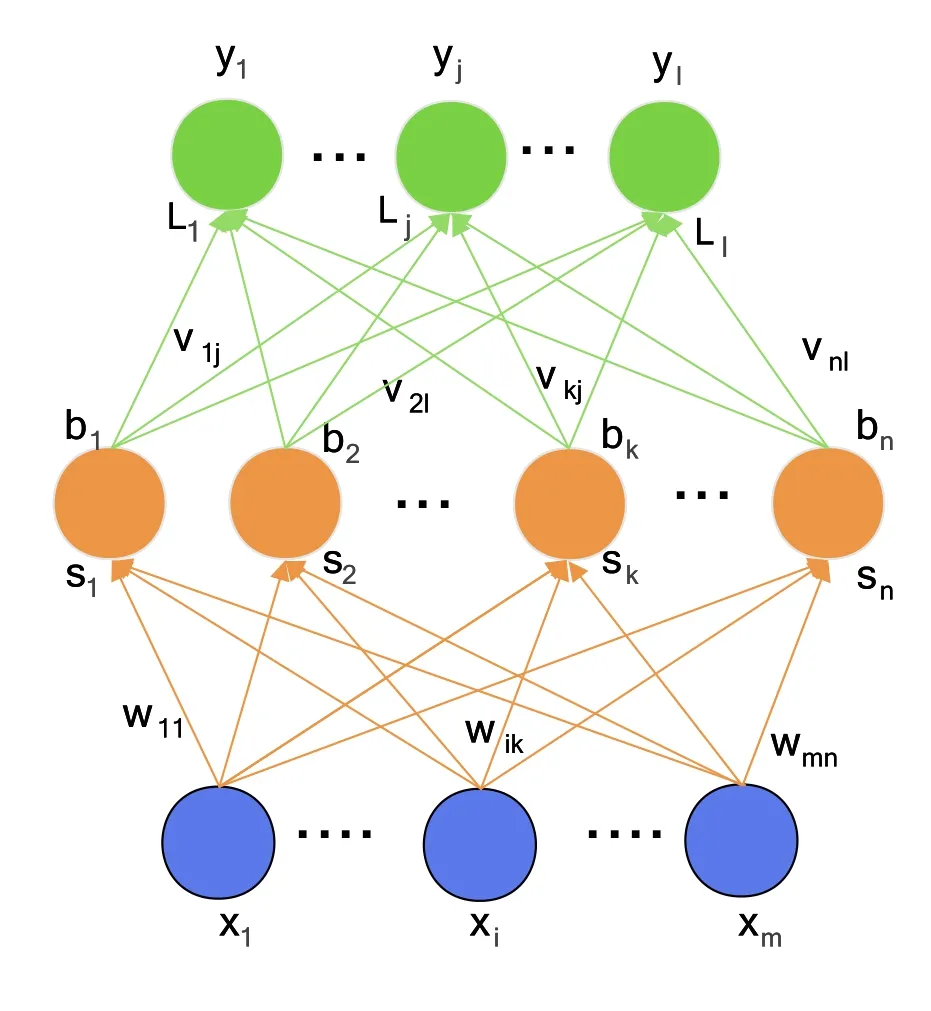
Figure 1.Structure model of BP-NN.
The BP-NN model consists of input layer,hidden layer and output layer.As shown in the Figure 1,it is a BP-NN containing a hidden layer.The normalized received signal matrix passes through the input layer,and then enters the hidden layer after calculating the weight and threshold value.Finally,the result from the output layer can be outputted.
3.2 Training Model of BP Neural Network
BP neural network is a kind of multi-layer feed forward network trained by error back propagation algorithm,which is one of the most widely used neural network models at present.
BP neural network is trained by supervised learning mode.When a pair of learning modes are provided to the network,the activation value of the neurons will propagate from the input layer through the hidden layers to the output layer,and each neuron in the output layer outputs the network response corresponding to the input mode.Then,according to the gradient descent method,the weights and thresholds of the neural network are optimized to minimize the convergence error.The training model of BP neural network is shown in Figure 2.The training steps of traditional BP neural network are as follows:
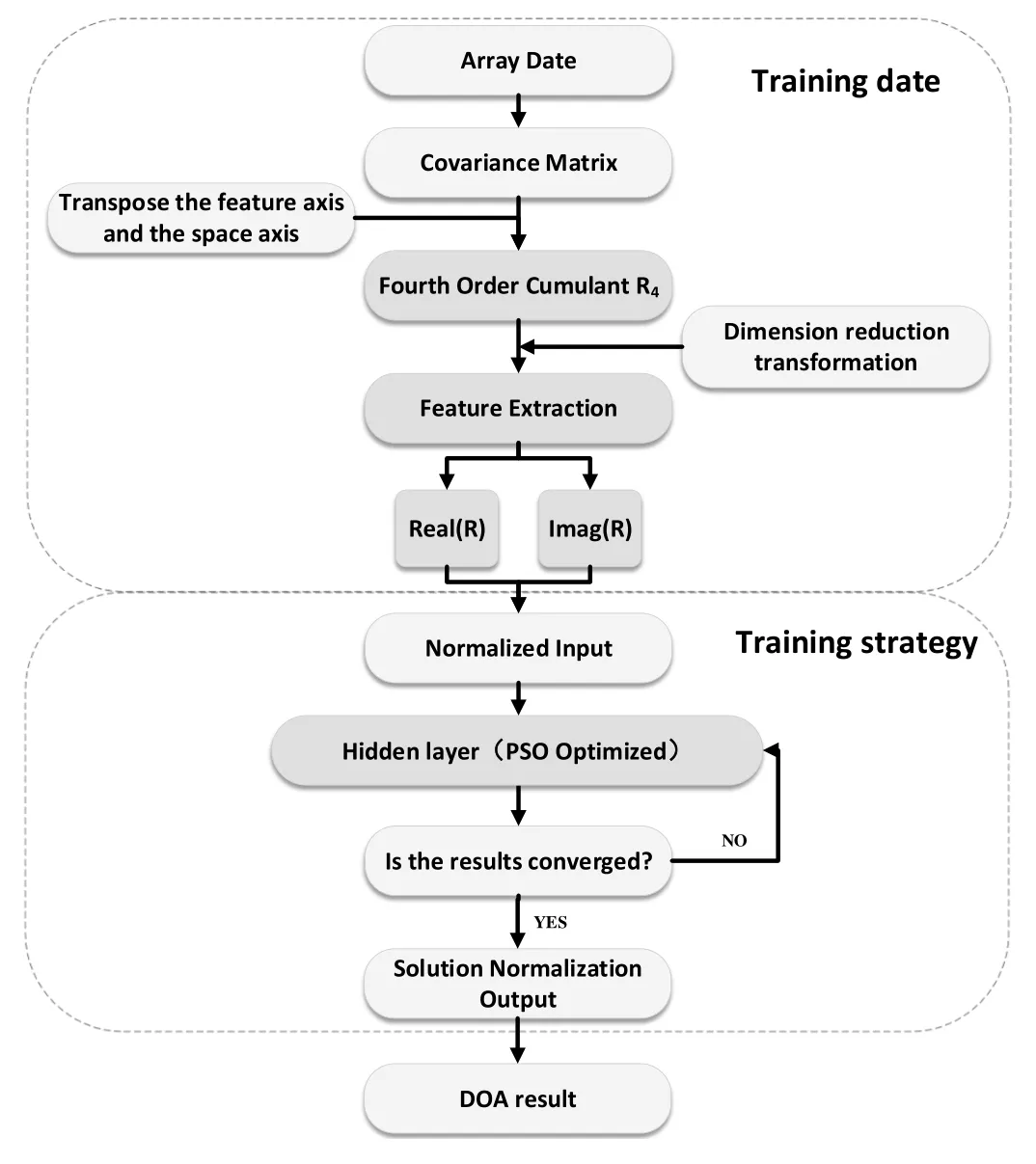
Figure 2.Optimization algorithm model.
1.Get the marked DOA data X of array signal;
2.The covariance matrix R of the received signal X is calculated according to equation(12),where the noise of the received signal X is assumed to be Gaussian white noise;
3.The eigenvalue decomposition of the covariance matrix R was carried out to find the eigenvectors corresponding to the first N eigenvalues;
4.The normalized eigenvectors are utilized as the test samples of the neural network;
5.Set the relevant parameters such as hidden layers,weights and thresholds and iterative accuracy of the neural network;
6.The training samples are input from the hidden layer of neural network and trained by gradient descent method;
7.Determine whether the error meets the preset accuracy or the maximum number of iterations.If the convergence conditions are met,the weight and threshold of each dimension in the global optimal value of the last iteration are the optimal solutions sought.If the convergence requirement is not met,proceed to step 6,and the algorithm continues to iterate;
8.After reaching the convergence requirements,the trained neural network is utilized to estimate the DOA.
3.3 Test Model of BP Neural Network
The test model of BP neural network is the process of substituting the array received signal X without DOA mark into the trained BP neural network model in subsection 3.2.In addition,the testing steps of traditional BP neural network are as follows:
1.Get unmarked DOA data X of array signal;
2.The covariance matrix R of the received signal X is calculated according to equation(12),where the noise of the received signal X is assumed to be Gaussian white noise;
3.The eigenvalue decomposition of the covariance matrix R was carried out to find the eigenvectors corresponding to the first N eigenvalues;
4.The normalized eigenvectors are utilized as the test samples of the neural network;
5.The test samples are put into the BP neural network model in subsection 3.2;
6.Through the operation of neural network model weight and threshold,the correct DOA estimation is output.
IV.OPTIMIZATION ALGORITHMS FOR BP NEURAL NETWORK
4.1 Optimized PSO-BP Neural Network Algorithm
4.1.1 Optimized PSO Algorithm
In subsection 3.2,the convergence method adopted for the training model of traditional BP neural network is gradient descent method,which is slow in convergence and easy to fall into local optimum.The PSO algorithm has the advantages of fast convergence and global convergence,which can optimize the iterative process of neural network.Therefore,this paper proposes a fast convergence model based on optimized PSO algorithm.
Inspired by the research results of artificial life,PSO algorithm is a global random search algorithm based on swarm intelligence by simulating the migration and flocking behavior of birds in the process of foraging.In PSO algorithm,individuals is referred to as particles.In the process of multi-dimensional search,particles change their search position by absorbing itself experience and group experience,and finally converge to the optimal value.
The steps of optimized PSO algorithm are as follows.
3.Equation (18) and (19) are the position updating process of particle swarm optimization
kis the updating times.wis the inertia factor.c1is the individual acceleration coefficient.c2is the swarm acceleration coefficient.c1=c2=2.r1andr2are values between 0 and 1;
4.Determine the fitness function.The Root Mean Square Error(RMSE)function of neural network training is utilized as thefitnessevaluation function of particles
In the formula,Tis the number of output samples.yl(r)is the true value of the lth sample output,andylis the ideal value of the lth sample output.Therefore,the position of the particle with the lowest fitness when the algorithm iteration stops is the optimal solution for the problem;
5.According to equation(18)and(19),the particle position is updated continuously to the optimal value until the convergence requirement is met.
In this paper,the weight factor of PSO algorithm is redefined to achieve the purpose of better optimization of BP-NN.
The weight factor of PSO algorithm in reference[33]is a fixed value from 0.4 to 0.9.However,in the case of large search range,the larger the weight factor of PSO algorithm is,the better the search is.When the search range is small,the smaller the weight factor is,the better the search is.We hope that when the PSO algorithm starts to iterate,the weight factor will be large,and the weight factor will gradually decrease with the increase of iteration times.Therefore,the weight factor is adjusted according to the number of iterations,
Where,Tmaxis the maximum number of iterations andtis the current number of iterations.In this paper,wmax=0.9.In equation (21),Tmaxrepresents the maximum iterations number of PSO algorithm.trepresents the current iteration number of PSO algorithm.
4.1.2 Optimized PSO-BP Neural Network Algorithm Model
In practical underwater DOA estimation,BP-NN algorithm has strong generalization ability.However,the BP-NN is prone to land oneself in local optimum solution during the iteration of weights and thresholds.In this paper,an optimized PSO algorithm is utilized to improve the performance of BP-NN,so as to form the PSO-BP-NN algorithm model.
In the process of DOA estimation,the eigenvector of the received signal covariance matrix R contains generous direction information.Therefore,in the case of a single source,the training sample of the neural network is the eigenvector corresponding to the largest eigenvalue of the Fourth-order cumulant matrix.Similarly,in the case ofNsources,the training samples of the neural network are the eigenvectors corresponding to the firstNlargest eigenvalues of the Fourth-order cumulant matrix.
Due to the training sample of neural network is complex,the real part and imaginary part of the training sample are separated.Therefore,the number of samples input to the neural network is twice that of the actual samples.
The steps of DOA estimation utilizing PSO-BP-NN are as follows.
1.Determine the size of the particle swarm and utilize particles as the threshold and the weight of the neural network.The model of neural network is M-N-2,the number of particles in each dimension selected in this papern=30,and the dimension of the particle ism=(M+N)×N+(N+1)×1;
2.Determine the learning factorsc1,c2and the convergence factorwproposed by equation(21);
3.Determine the fitness function of particles by equation(20);
4.The training samples are input from the hidden layer of neural network;
5.Update the position and velocity of particles according to equation(18)and(19);
6.Determine whether the error meets the preset accuracy or the maximum number of iterations.If the convergence conditions are met,the weight and threshold of each dimension in the global optimal value of the last iteration are the optimal solutions sought.If the convergence requirement is not met,proceed to step 3,and the algorithm continues to iterate;
7.The optimized weights and thresholds are brought into BP-NN,and then the training samples are trained by the minimum gradient method to make it reach the specified accuracy,so as to estimate the signal DOA.
4.2 BP Neural Network Algorithm Based on Fourth-order Cumulant Optimization
In subsection 3.3,the noise of the test signal of traditional BP neural network is assumed to be Gaussian white noise.When the noise in the training model is Gaussian white noise,the traditional DOA estimation algorithm is based on the covariance matrix of the received data signal.In the actual underwater DOA estimation,the noise can be variable,such as Gaussian colored noise.At this time,the statistical characteristics described by the First-and Second-order statistics of the signal are not comprehensive.If the DOA estimation continues through the traditional algorithm,the accuracy of DOA estimation will be greatly reduced or even wrong.Due to the High-order cumulant can suppress the additive Gaussian colored noise better,the Third-order cumulant of the received signal is usually zero when the random process of the received signal satisfies the symmetric distribution.For symmetric distributed stochastic processes with small Third-order cumulant,the Fourth-order cumulant are usually larger[39–41].So this paper utilizes Fourth-order cumulant to enhance the robustness of DOA estimation model.
4.2.1 The Definition of Fourth-Order Cumulant
The Fourth-order cumulant of n-dimensional zero mean stationary stochastic processxsatisfy
4.2.2 Derivation of Fourth-Order Cumulant of Received Data
When the received signal by array does not obey Gaussian distribution and the additive noise is Gaussian noise,the conclusion can be drawed from reference[42].This is because the cumulants of two statistically independent stochastic processes satisfy the independent additive property.
Due to the Fourth-order cumulant can suppress the colored Gaussian noise,the results are as follows.
Whereal(h) is the hth element of the lth steering vector.Suppose the signal sourcessl(t)(l=1,2,...,q) are independent with each other,the equation(25)can be simplified as
Whereγ4slis a Fourth-order cumulant matrix.Then the value range ofh1,h2,h3,h4in equation (26) is 1≤h1,h2,h3,h4≤p.pis the number of array elements,for different sets of values ofh1,h2,h3,h4,a total ofp4values can be obtained.Generally,the matrixis utilized to place these Fourth-order cumulant,and their values are as
According to the definitions of equations (26)and(27),the following Fourth-order cumulant matrix is obtained
Where⊗is the Kronecker Product.The array received signal X is brought into equation(28)to obtain R4,which can effectively suppress the interference of Gaussian colored noise on the received signal and improve the DOA estimation accuracy.
4.2.3 BP Neural Network Algorithm Model Based on Fourth-Order Cumulant Optimization
The Fourth-order cumulant can suppress the colored Gaussian noise.Therefore,this paper utilizes BP-NN algorithm based on Fourth-order cumulant optimization to estimate DOA.
The steps of DOA estimation algorithm of BP-NN based on Fourth-order cumulant optimization are as follows.
1.The covariance matrix R of the received signal X is calculated according to equation(12);
2.According to the equation (28),the Fourth-order cumulant matrix R4of array received signal X is obtained;
3.Perform eigenvalue decomposition on R4,find the eigenvectors corresponding to the firstNargest feature values,and then utilize the eigenvectors as the input of the neural network after normalization;
4.Set the relevant parameters such as hidden layers,weights and thresholds and iterative accuracy of the neural network;
5.The training samples are input from the hidden layer of neural network and trained by gradient descent method;
6.After reaching the convergence requirements,the trained neural network is utilized to estimate the DOA.
4.3 Multi-Source Underwater DOA Estimation of PSO-BP-NN Based on High-Order Cumulant Optimization
The traditional neural network algorithm [43,44] often assumes that there is only one or two signal sources,but this is obviously not consistent with the actual situation.Therefore,this paper proposes a DOA estimation algorithm for the number of arbitrary sources based on optimized neural network.In addition,the subsection 4.2 and subsection 4.3 algorithms proposed in this paper are extended to the case of arbitrary sources,thus forming a multi-source DOA estimation model using PSO-BP neural network based on High-order cumulant optimization.
The DOA estimation steps of arbitrary source number of PSO-BP-NN based on Fourth-order cumulant optimization are as follows.
1.The covariance matrix R of the received signal X is calculated according to equation(12);
2.According to the equation (28),the Fourth-order cumulant matrix R4of array received signal X is obtained;
3.Perform eigenvalue decomposition on R4,find the eigenvectors corresponding to the firstNargest feature values,and then utilize the eigenvectors as the input of the neural network after normalization;
4.Set the relevant parameters such as hidden layers,weights and thresholds of the neural network;
5.Utilize the mean square error value of the neural network in equation(20)as the fitness evaluation standard of the PSO algorithm,and input training samples to train the neural network;
6.The weights and thresholds which meet the convergence requirements are regarded as the initial weights and thresholds of PSO-BP-NN,and then BP algorithm is utilized to train the neural network to achieve the specified accuracy;
7.After reaching the convergence requirements,the trained neural network is utilized to estimate the DOA.
The simulation results show that when the received signal noise is Gaussian colored noise,the proposed algorithm has higher estimation accuracy,faster convergence speed and superior universality than the traditional BP neural network algorithm and the MUSIC algorithm.
V.SIMULATION
In this section,the algorithm proposed in this paper is compared with the traditional BP-NN and MUSIC algorithms to verify the superiority of the proposed algorithm.
The array selected in this paper is a Uniform Linear Array (ULA).In this simulation,the number of array elements is set to be 10,the source frequent is 1kHz and the inter-element space is set to be half of the wavelength.The number of snapshots is set to 500.In addition,the array sensors are omnidirectional and uncoupled,in which the direction vector of the received signal can be expressed as:
Whereλis shown above.The distance between two adjacent array elements on the ULA isd.In this simulations,d=
In this paper,the general expression ofSNRis
sl(t)is the lth signal received at a certain timet.σ2is an unknown real number.
5.1 Effectiveness of PSO-BP Neural Network Algorithm
When the noise in the training model is Gaussian white noise,Figure 3 shows the performance comparison between the optimized PSO-BP-NN algorithm and the BP-NN algorithm.In this experiment,the number of array elements is set to be 10,the number of snapshots is set to 500,single source and double sources are discussed respectively.(1) In the case of single source,the training samples were taken from [-90,90],and the step size is 0.5 degrees.The testing samples size were taken from [-90,90],with a step size of 1 degree.(2)In the case of double sources,the spacing between the double sources are 2°,3°,5°,7°,10°,15°,20°,30°,40°,50°and 60°.When the spacing is 5°,a group of samples are generated every degree between[-90,85].When the spacing is 15°,the same number of samples are also generated every degree between[-90,75].Similarly,other training samples can be obtained.In the range of [-90,90],two samples with source spacings of 25.5°was randomly selected as testing samples.Two conclusions can be drawn from Figure 3.(1) The optimized PSO-BP-NN algorithm is more accurate than the traditional BP-NN algorithm in DOA estimation.(2)The optimized PSO algorithm can avoid the defect that traditional BP neural network is prone to fall into local optimal.
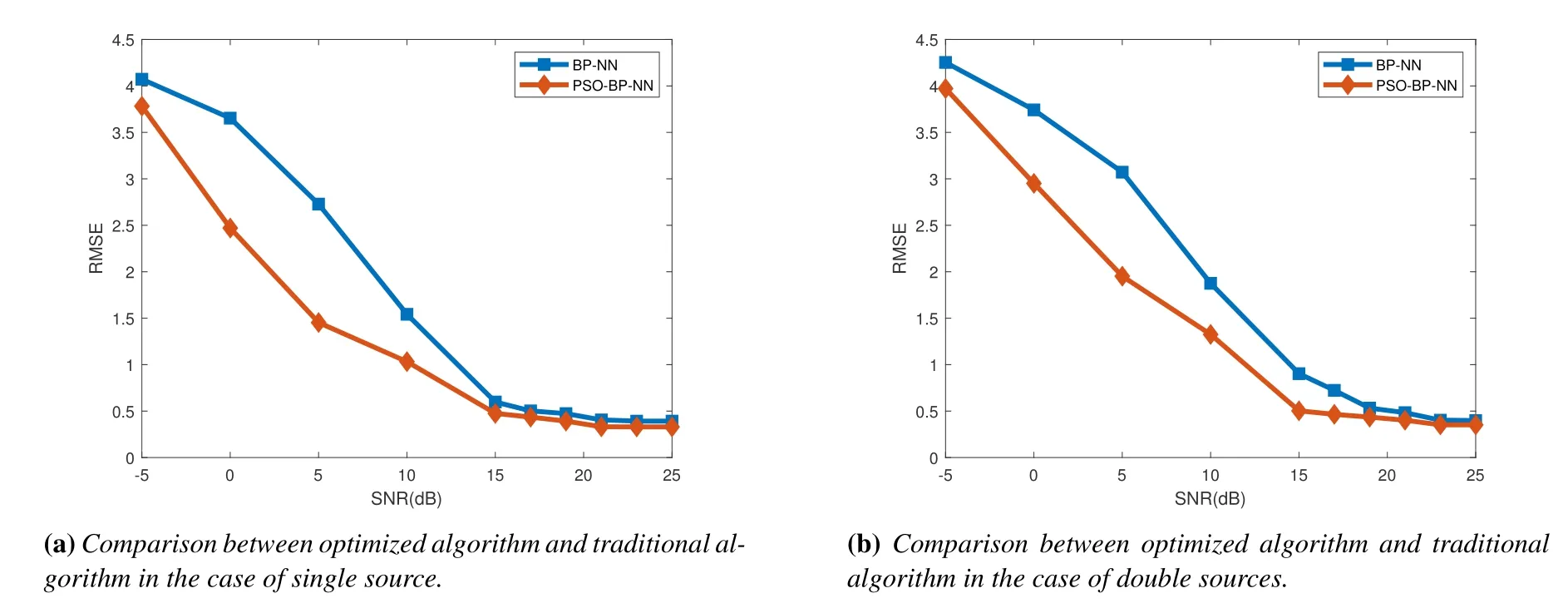
Figure 3.RMSE comparison between PSO-BP-NN and traditional BP-NN.
5.2 Effectiveness of Fourth-Order Cumulant Algorithm
The RMSE comparison between the optimized BPNN algorithm based on Foure-order cumulant and the traditional BP-NN algorithm is shown in Figure 4(b)and (d).The relationship between the testing sample of the optimized algorithm and the actual output is shown in Figure 4(a)and(c).In this experiment,the number of array elements is set to be 10,the number of snapshots is set to 500,single source and double sources are discussed respectively.(1) In the case of single source,the training samples were taken from[-90,90],with a step size is 0.5 degrees.The testing samples were taken from[-90,90],with a step size of 1 degree.These test samples were selected under the condition that the received signal noise was Gaussian noise.(2) In the case of double sources,the spacing between the double sources are 2°,3°,5°,7°,10°,15°,20°,30°,40°,50°and 60°.In the range of[-90,90],two samples with source spacings of 17°,25°,and 36°were randomly selected as testing samples.These test samples were selected under the condition that the received signal noise was Gaussian noise.As can be seen from Figure 4,when the received signal noise is Gaussian color noise,the traditional BP-NN algorithm has obvious errors in DOA estimation.Especially at low SNR,the optimized algorithm has better accuracy than the traditional BP-NN algorithm.
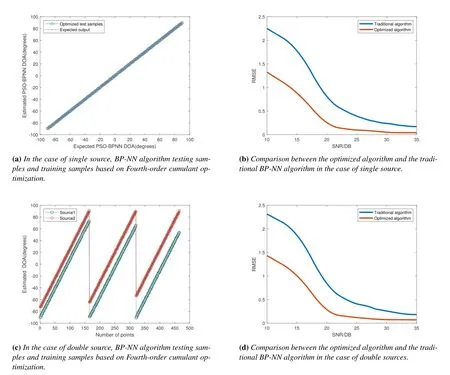
Figure 4.Comparison between the algorithm based on Fourth-Order Cumulant optimization and the traditional algorithm.
5.3 Effectiveness of BP-NN Algorithm with Arbitrary Number of Sources
Figure 5(a)and(b)shows the DOA estimation of arbitrary source proposed in this paper (taking three and four sources as examples).In this experiment,the number of array elements is set to be 10,the number of snapshots is set to 500,SNR is set to be 20dB.In the case of three sources,the spacing between the three sources are 2°,3°,5°,7°,10°,15°,20°,30°,40°,50°and 60°.In the range of[-90,90],three samples with source spacings of 13°,21°,and 30°were randomly selected as testing samples.In the case of four sources,the spacing between the four sources are 2°,3°,5°,7°,10°,15°,20°,25°,30°,40°,50°and 55°.In the range of[-90,90],four samples with source spacings of 13°,21°,and 30°were randomly selected as testing samples.Figure 5(c) and (d) show the DOA estimation error with three and four sources.The simulation results in Figure 5(a)and(b)show that the optimized algorithm has certain universality for DOA estimation of arbitrary number of sources.The simulation results in Figure 5(c)and(d)show that the error of DOA estimation increases with the increase of the number of sources.
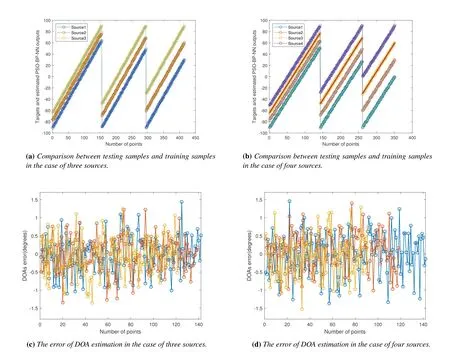
Figure 5.Comparison of test samples and training samples with arbitrary number of sources.
Figure 6 shows the performance comparison between RMSE and the number of sources.The experimental conditions in this paper are divided into two cases:(1)we setSNR=5dB,p=10 and the signals are independent.(2) we setSNR=15dB,p=10 and the signals are independent.The optimization algorithm is compared with MUSIC[12]algorithm and state-of-the-art methods [28,29].In addition,in Figure 6(a) and (b),500 independent trials were carried out under each source.As can be seen from Figure 6(a)and(b),when the noise of the array received signal is Gaussian colored noise,the RMSE of the four algorithms gradually increases with the increase of the number of sources.However,whenSNR=15dB,the DOA estimation accuracy of the optimization algorithm is better than the state-of-the-art methods and MUSIC algorithm.In addition,whenSNR=5dB,the performance of the proposed algorithm is the same as CNN[29]algorithm,which is better than DNN[28]algorithm and MUSIC [12] algorithm.The results show that the optimization algorithm can effectively improve the accuracy and robustness of DOA estimation model.
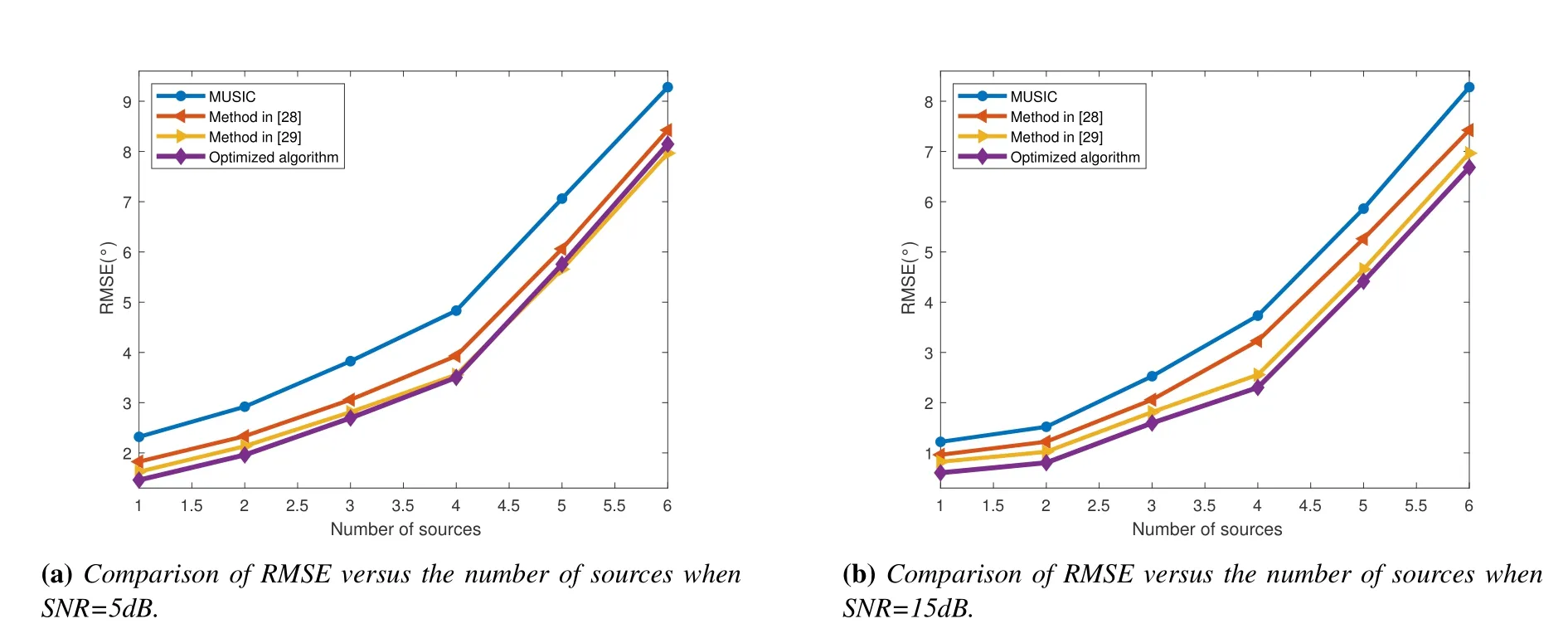
Figure 6.Performance comparison between RMSE and number of sources.
5.4 Effectiveness of Optimization Algorithm for Coherent Signals Processing
Due to the sound scatterers,multi-path signals and other factors in underwater acoustic channel,the coherent signals exist widely.The existence of coherent signals will lead to the rank deficiency of the covariance matrix.When MUSIC algorithm processes coherent signals,decoherence processing is needed.Standard decorrelation algorithms include spatial smoothing algorithm [45] and Toeplitz matrix reconstruction algorithm [46].Since spatial smoothing will introduce the array aperture’s loss,we can utilize Toeplitz reconstruction algorithm to obtain the decorrelation covariance matrix before estimating DOA.
MUSIC algorithm belongs to the traditional mathematical model,which needs to utilize the decoherence algorithm for DOA estimation.However,the DOA estimation algorithm based on neural network model has strong generalization and mapping ability,which not needs to utilize the decoherence algorithm for DOA estimation.
In addition,in order to improve the universality of neural network,this paper increases the training of coherent signals by neural network,which makes the training sample multiply.In this simulation,the frequency of coherent sources is 1kHz,the frequency of independent source is 1.5kHz,the number of array elementsp=10 and the inter-elementspace was set to be half of the wavelength.
First,we verify the convergence performance of the optimized PSO algorithm in the presence of coherent signals.This simulation is divided into two parts: (1)two sources,source 1 and source 2 are coherent signals.(2) Three sources,source 1 and source 2 are coherent signals,and source 3 is independent signal.As can be seen from Figure 7,compared with traditional BP-NN algorithm,the optimized PSO algorithm can minimize the loss of training and validation of the network and accelerate network convergence,which is the same as the independent signals.
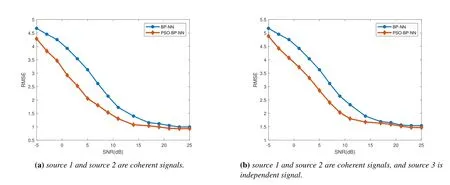
Figure 7.RMSE comparison between PSO-BP-NN and traditional BP-NN.
Finally,the statistical performance of PSO-BP-NN algorithm,MUSIC [12] algorithm,[28] and [29] algorithms are verified when the received signal noise is Gaussian colored noise.This simulation is divided into two cases: (1)two sources,source 1 and source 2 are coherent signals.(2) Three sources,source 1 and source 2 are coherent signals,and source 3 is independent signal.In addition,in Figure 8(a) and (b),500 independent trials were carried out under each SNR.We can see that when the signal is coherent,the experimental results show that after decoherence processing by [40],the algorithm proposed in this paper has higher accuracy,stronger robustness and universality than MUSIC algorithm and state-of-the-art methods.Obviously,with the application of decoherence technology,the DOA estimation accuracy of MUSIC algorithm is significantly reduced.
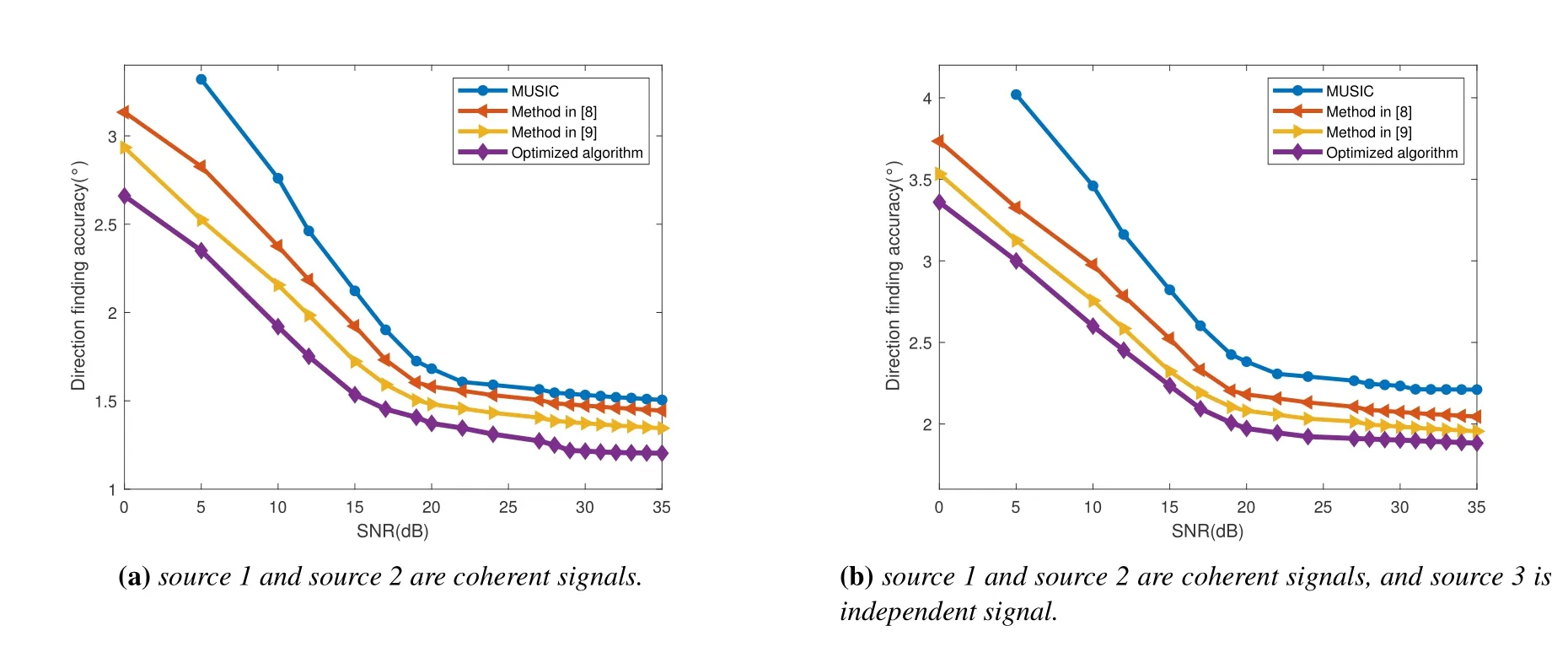
Figure 8.The statistical performance is compared when the received signal noise is Gaussian colored noise.
5.5 Comprehensive Simulation Experiment and Comparison
Figure 9 shows the effect of different training samples on DOA estimation accuracy.In this experiment,the number of array elements is set to be 10,the number of snapshots is set to 500,SNR is set to be 20dB.This simulation is divided into two cases:single source and double sources.(1) In the case of single source,the training samples were taken from [-90,90],and the step sizes are divided into 2°,0.5°and 0.1°,respectively.The testing samples were taken from[-90,90],with a step size of 1°.(2)In the case of double sources,the number of training samples is divided into three cases.1) the spacing between the double sources are 2°,7°,10°,20°,40°,and 60°.2)the spacing between the double sources are 2°,3°,5°,7°,10°,15°,20°,30°,40°,50°and 60°.3) the spacing between the double sources are 2°,3°,5°,7°,10°,15°,20°,25°,30°,35°,40°,45°,50°,50°and 60°.In the range of[-90,90],two samples with source spacings of 27°was randomly selected as testing samples.Figure 9 shows the effect of the number of training samples on the accuracy of DOA estimation.From Figure 9(c)and (d),it can be concluded that the higher the accuracy of DOA estimation is with the increase of training samples.
Figure 10 shows the statistical performance comparison when the received signal noise is Gaussian colored noise.In this experiment,we setp=10,the number of snapshots is set to 500 and the signals are independent.This simulation is divided into two cases: single source and double sources.In addition,in Figure 10(a)and(b),500 independent trials were carried out under each SNR.Due to the change of noise environment in methods [28] and [29],the DOA estimation accuracy of these two methods is reduced.We can see that the estimation accuracy predominance of the optimized algorithm is over state-ofthe-art [28,29] methods and MUSIC [12] algorithm,which indicates that optimized algorithm can effectively improve the accuracy of DOA estimation.
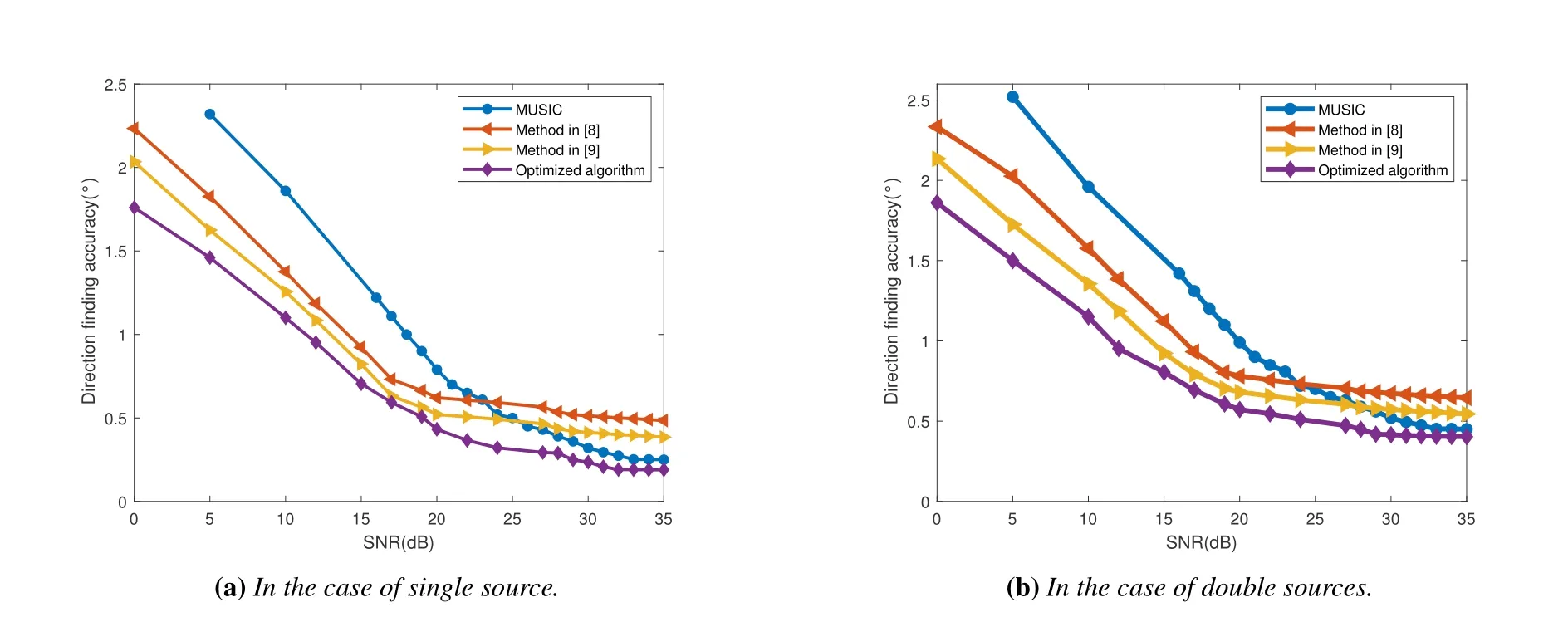
Figure 10.The statistical performance is compared when the received signal noise is Gaussian colored noise.
VI.CONCLUSION
This paper utilizes BP neural network to estimate DOA.Aiming at the problems existing in the traditional BP neural network,this paper proposes the following three improvements.First,the BP-NN algorithm is trained by gradient descent method,which is prone to land oneself in local optimum solution in the training process,thus affecting the accuracy of DOA estimation.To overcome this problem,this paper proposes to utilize PSO algorithm to optimize BP neural network,and improves the weight factor of PSO algorithm to form PSO-BP-NN algorithm.Second,in the actual underwater DOA estimation,the noise of the received signal is often not Gaussian white noise,but complex and changeable noise,such as Gaussian color noise.Then,this paper utilizes the high-order cumulant of the received signal to establish the training model,so as to effectively combat the complex and changeable underwater noise.Thirdly,in the actual environment,the number of received sources may be not single.Therefore,this paper raised a method which can process arbitrary number of received signals.The simulation results show that the three improvements can increase the accuracy of DOA estimation in Gaussian colored noise environment and improve the universality of DOA estimation.
ACKNOWLEDGEMENT
This work was supported by the following funds,Strategic Priority Research Program of Chinese Academy of Sciences,Grant No.XDA28040000 and XDA28 120000;Natural Science Foundation of Shandong Province,Grant No.ZR2021MF094;Key R &D Plan of Shandong Province,Grant No.2020CXGC 010804;Central Leading Local Science and Technology Development Special Fund Project,Grant No.YDZX2 021122;Science &Technology Specific Projects in Agricultural High-tech Industrial Demonstration Area of the Yellow River Delta,Grant No.2022SZX11.
杂志排行
China Communications的其它文章
- IoV and Blockchain-Enabled Driving Guidance Strategy in Complex Traffic Environment
- Multi-Objective Optimization for NOMA-Based Mobile Edge Computing Offloading by Maximizing System Utility
- LDA-ID:An LDA-Based Framework for Real-Time Network Intrusion Detection
- A Privacy-Preserving Federated Learning Algorithm for Intelligent Inspection in Pumped Storage Power Station
- Secure Short-Packet Transmission in Uplink Massive MU-MIMO Assisted URLLC Under Imperfect CSI
- An Efficient Federated Learning Framework Deployed in Resource-Constrained IoV:User Selection and Learning Time Optimization Schemes
