无线紫外光通信下基于改进人工势场法的无人机编队控制研究*
2023-12-09高运克唐宏伟高方坤丁祥罗佳强王军权
高运克,唐宏伟,高方坤,丁祥,罗佳强,王军权
(邵阳学院多电源地区电网运行与控制湖南省重点实验室,湖南 邵阳 42200)
现有的无人机编队控制方法主要有领航者跟随者(Leader-Follower)方法[1]、基于行为的方法、虚拟结构方法[2]、基于人工势场避障的方法[3]、基于一致性理论的方法等。各种方法各有优缺,广泛应用于无人机编队控制领域。
文献[5]将斥力势场函数拆分成分段连续的形式,以此避免编队避障过程出现的急促转弯和频繁大转角,通过增加虚拟障碍物避免出现局部极小问题,并利用Bezier 曲线特点对飞行轨迹进行实时优化;文献[6]结合了模糊控制算法,成功破坏了局部极小值位置的平衡状态,还基于无人机的相对速度和动态障碍物构造了相对速度势场;文献[7]提出提前生成预规划路径,弱化目标位置对无人机编队的引力作用,并在多条预规划路径中选定出能避免局部最优的一条路径,但该方法不适用于高速动态下的复杂环境;文献[8]通过设置碰撞预测机制,提出了基于传统人工势场避障算法并且能够进行安全避障的编队生成和保持算法,即通过改变无人机编队中虚拟领航者的相对位置来实现队形重构,从而完成编队安全避障;文献[9]将周围的其他无人机也视作动态障碍物,提出了一种不需要获知相邻无人机飞行信息也可进行无人机安全避障和编队控制的算法;文献[10]利用指数函数的特征,在平衡点处构造了对称且最大值有界的势场,在势场系数计算时能够考虑到无人机运动状态的条件限制,但该算法无法解决平衡点附近路径振荡问题,遇到动态障碍物的情况也不适用;文献[11]是基于无人机编队前进方向的向量来改进斥力产生机制,并设立虚拟引导点应对产生的局部最优问题;文献[12]通过对最大转弯角进行约束来缓解局部振荡问题,并优化威胁区的模型,但仍具有局限性。
现有人工势场避障算法少有综合考虑到无人机编队同时面对来自外部的局部极小值与路径振荡问题、以及邻近无人机这一动态障碍物产生编队内部撞机事件的可能性,在这个方向上值得进一步深入研究。
1.1 无线紫外光通信
由于无线紫外光通信(Uitraviolet Communications,UVC)[13]具有局域保密性好、抗干扰能力强、背景噪声小的优点,将其作为无人机集群运行时的通信手段,即使在复杂环境下,无人机集群也可以保持稳定通信并进行信息共享。
无线紫外光通信是发射装置发射出载有无人机状态信息的紫外光经大气信道中的气溶胶等微粒散射,最终被接收装置探测吸收,由于气溶胶等微粒散射作用,无线紫外光通信不仅支持直视通信,还支持非直视通信。而根据发射端光束的发射角和接收端的接收视场角关系,直视通信可以分为三种类型:如图1所示的(a)类通信方式、(b)类通信方式和(c)类通信方式[14]。
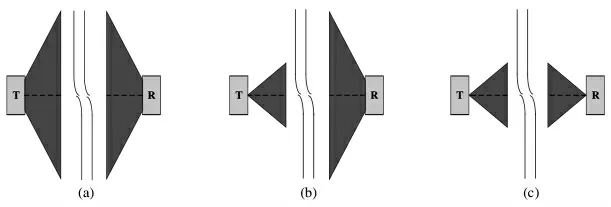
图1 无线紫外光直视通信
无线紫外光直视链路在大气自由空间下的功率损失呈现指数衰减,大气衰减可表示为e-Ker,自由空间路径功率损耗跟通信距离的平方成正比,即通信距离r越大,功率损耗越大,接收器接收到的能量与r2可以表示为信号接收器的接收增益为,其中λ是无线紫外光的波长,由此可得出无线紫外光通信链路直视通信情况下的接收光功率的表达式如式(1)[15]
可简化为:
其中,Pt是发射器发出的光功率;Ke是大气信道衰减系数;Ar是接收器的孔径面积。
在无线紫外光通信中,传输效率定义为发送功率与接收功率的比值,表征信号从发射端到接收端之间信号衰减的大小,传输效率可以表示为:
1.2 传统人工势场法
人工势场法是1986年Khatib[16]提出的理论,其基本思想是将整个环境看成一个巨大的人造势场模型,将在这个势场范围内的无人机、障碍物等看成质点,无人机在势场范围内会受到两种类型力的作用,其中无人机集群的目标点产生吸引力势场,而阻碍无人机到达目标点的障碍物则产生排斥力势场,无人机在吸引力与排斥力产生的合力作用下,从起点到达目标点。
在三维空间中,环境势场定义在三维空间0-xyz中,无人机的空间坐标可以表示为X=(x,y,z),目标点的坐标为Xg=(xg,yg,zg),碰撞威胁物的坐标为X0=(x0,y0,z0),无人机到达目标点之前一直受到目标点的吸引力影响,目标点的吸引力随着无人机距离的靠近逐渐减小,当无人机达到目的地,吸引力就会变成零,目标点产生的引力场函数为:
其中Ua(X)为引力场函数,ka为引力势场常系数,d(X,Xg)=‖X-Xg‖为无人机到目标点的距离。
无人机受到目标点的吸引力Fa(X)是沿着引力势场Ua(X)的负梯度方向,在无人机与目标点连线上并且指向目标点,即:
与引力场函数相似,斥力势场函数也是与无人机到障碍物之间的距离有关,设d0为无人机到障碍物的最大威胁距离,当无人机与障碍物的距离小于等于d0时,障碍物才会对无人机产生斥力作用,此时无人机不断靠近障碍物,受到的障碍物产生的斥力逐渐增大,由此得出障碍物产生的斥力场函数为:
其中Ur(X)为斥力场函数,kr是斥力场常系数,d(X,X0)=‖X-X0‖是无人机到障碍物的实时距离。
由公式(6)可推导出障碍物对无人机的斥力Fr(X),方向是沿着无人机与障碍物的连线上并指向无人机:
在人工势场中,势场函数定义为:
由拉格朗日方程和空间动力学可从公式(8)推出无人机在势场中受到目标点和障碍物的势场力为:
由于无人机在势场中不只受到单个障碍物的作用,所以公式(9)还不是引导无人机安全达到目标点的飞行方向指导力,势场中的无人机是靠着来自目标点的引力与多个障碍物产生的斥力的合力作为飞行方向,从而达到目标点,因此单个无人机所受到的势场力可以表示为:
2 改进人工势场法
正常情况下无人机按照公式(10)算法计算出的合力Fall(X)提供的飞行方向就能流畅地避开障碍物,成功到达目标集结点,但实际应用中不可避免会出现下面两种情况。
(1)局部极小值问题
在理想情况下,当无人机顺利到达目标点时,受到的吸引力和斥力的合力变成全局最小,但当目标点的吸引力与障碍物排斥力的合力在同一条直线上,大小相等方向相反时,此时无人机受到的势场合力为0,无人机主观以为到达了目标点而停止运行,这明显是不正确的,无人机被困在一个局部极小值区域内。
为了解决上述局部极小值现象,如图2所示,在无人机处于局部极小值的地方与目标集结点之间的法平面,计划通过在法平面上选择一个能产生水平方向力的附加势场,使无人机能与目标集结点连线垂直方向且同时平行水平面的方向移动,从而跳出局部极小值点。
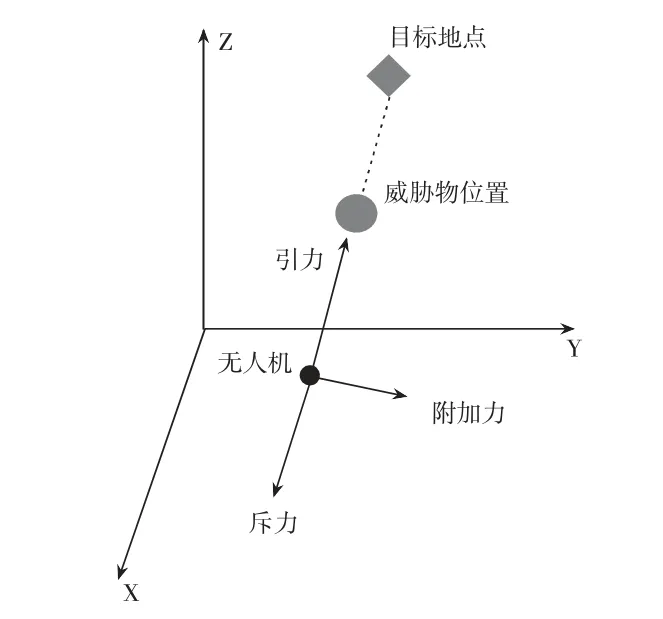
图2 附加势场示意图
附加势场函数为:
式中Xmin为无人机陷入极小值时的坐标,dadd是附加力作用的最远距离,k是一个正整数。
(2)局部路径振荡问题
当无人机在运行途中,在k时刻的位置为Xk(xk,yk,zk),此时目标点对无人机的吸引力大于障碍物的排斥力,处于主导地位,无人机会朝着目标点所在位置前进,但同时也在不断靠近障碍物,障碍物的排斥力逐渐增大,当来到k+1时刻,此时的位置是Xk+1(xk+1,yk+1,zk+1),障碍物的排斥力大于目标点的吸引力,此时障碍物产生的排斥力占据无人机运行方向的主导地位,无人机会向远离障碍物的方向飞行,同时远离目标点。在一段时间内排斥力和吸引力交替占据主导地位,导致临近路径点无人机受到的合力方向频繁发生变化,具体表现在无人机运行轨迹上产生振荡现象,无人机机群的振荡问题对集群冲击较大,很容易产生炸机现象,导致无人机集群系统崩溃,不得不予以重视。
如图3所示为无人机产生局部振荡问题时实际路径的情况,本文采用重新计算新合力的方法来应对振荡问题,假设无人机在k时刻的Xk(xk,yk,zk)位置发生振荡,按照正常的人工势场进行会根据当前目标点和障碍物的位置情况计算合力F1,通过合力作用到达k+1时刻的Xk+1(xk+1,yk+1,zk+1),当计算出下一路径点的合力F1之后,再与之前从k-1时刻到k时刻的合力F2一起来计算新的合力F3,无人机到达k+1时刻使用的合力由F2变成了F3,通过中和前后两个时刻点的合力方向进而减少实际合力的角度变化量,从而实时改善无人机局部振荡问题。
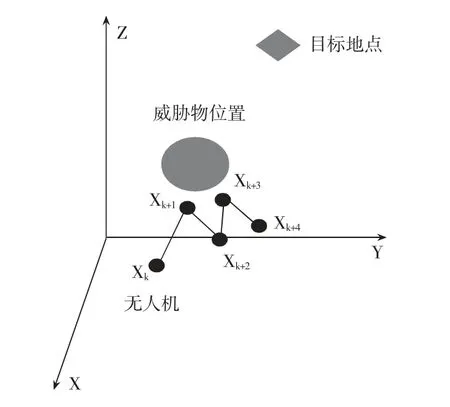
图3 路径振荡现象
加入二次计算合力的数学表达式如式(12)所示:
其中D是无人机在两个单位振荡路径点的实际飞行长度,Fk和Fk+1分别是人工势场法计算出来的到达位置Xk和Xk+1的合力,a和b是两个路径点的权重因子,其取值大小由二次合力的角度变化量△δ决定[17],并且a+b=1。
3 系统控制流程
对于传统人工势场中静态障碍物容易发生的局部极小值和路径振荡问题对人工势场进行改进,使用增加附加力和二次合力计算手段来应对局部极小值和路径振荡问题,系统流程如图4所示。
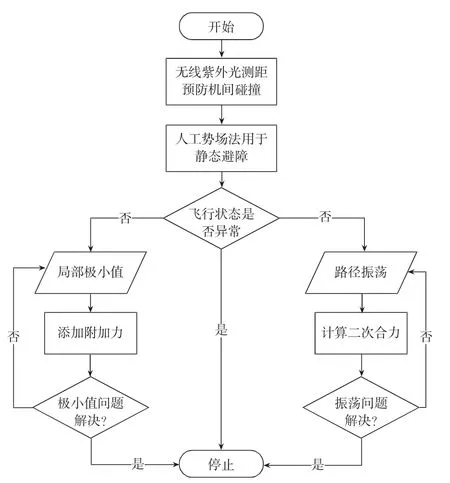
图4 系统流程图
4 系统实验及分析
对搭载人工势场算法的无人机集群进行仿真实验,仿真实验平台是Matlab2021a,通过人为构造局部极小值和路径振荡现象,分别使用传统人工势场算法和改进后的人工势场来进行对比实验,观察改进式人工势场算法(Improvement Artificial Potential Field,IAPF) 是否能有效解决局部极小值和路径振荡问题。仿真参数如表1所示。

表1 仿真通用参数选取
4.1 局部极小值问题仿真与分析
针对无人机飞行避障时经常出现的路径振荡问题和局部极小值问题,比较传统人工势场和改进人工势场,首先验证局部极小值问题是否成功,设定起始点在(0,0,0)、目标位置在(10,10,10)、碰撞威胁物(5,5,5),这个场景下无人机、目标点、威胁膨胀物会在飞行路径上连成一条直线,从而人为构成出局部极小值的现象,如图5所示为实验的具体情况。其中图5(a)是无人机在预定条件下分别按照传统人工势场法和搭载改进人工势场法计算出的全局飞行路径,图5(b)则是图5(a)中标注的“1”的放大情况,方便进行理论分析,图5(c)是无人机路径点与碰撞威胁物的距离情况统计,图5(d)是无人机行进路程点与目标集结点的距离统计。

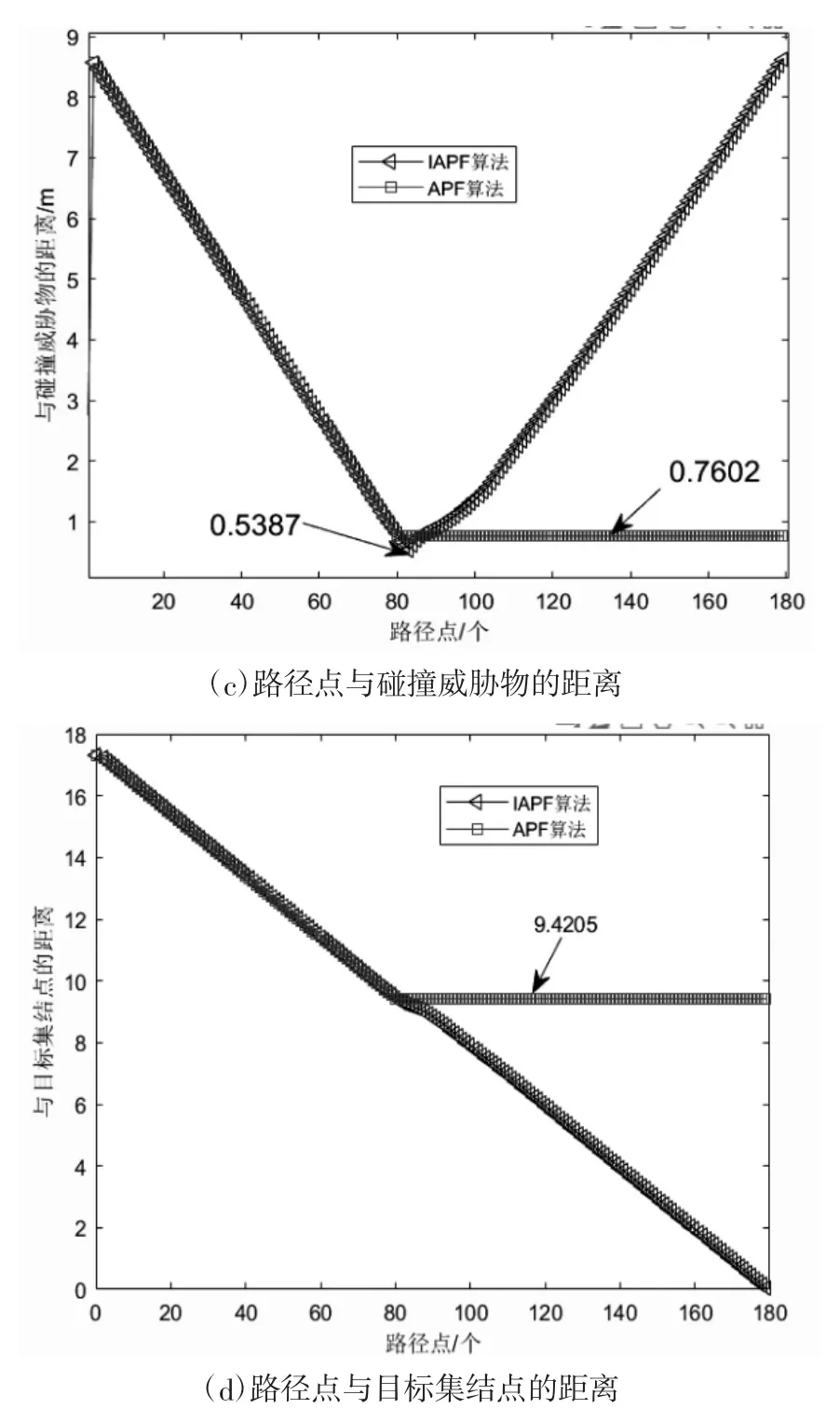
图5 局部极小值实验情况
从图5(a)和图5(b)中可以看出,在仿真实验刚开始时,距离碰撞障碍物较远,两种算法计算出的路径近乎一致,但传统人工势场算法航行到坐标(4.61,4.61,4.61)时,无人机飞行状态陷入了局部极小值点,没有能够成功绕过障碍物。而改进后的人工势场法在坐标(4.61,4.61,4.61)时同样进入到了局部极小值位置,此时通过计算与目标点之间的距离关系,判断出处于局部极小值状态,测试在当前位置与目标集结点之间连线的垂直方向,且平行于水平面的方向上增加附加力,附加力作用的路径长度是0.3m,作用完之后就消失,从图5(a)运行轨迹上很明显地看出附加力成功帮助无人机飞出了极小值点,摆脱了极小值状态。
从图5(c)和图5(d)无人机路径轨迹点与障碍物和目标位置的距离关系可知,传统人工势场是在距离障碍物0.760m时陷入了局部极小值,停止前进,而此时距离飞行任务目标位置还有9.420m,改进之后的人工势场算法同样在距离障碍物0.538m时陷入了局部极小值,在此时增加了附加力,使无人机成功跳出了局部极小值位置。
4.2 路径振荡问题仿真与分析
对路径振荡问题进行仿真实验,设定无人机起始位置在(0,0,0)、障碍物坐标在(18.5,18.5,19)、目标点坐标在(20,20,20),人为制造路径振荡问题的发生,通过观察传统和改进之后人工势场的运行情况,来验证改进人工势场能否解决路径振荡问题。如图6所示为记录仿真实验室的数据情况,其中图6(a)是无人机在预定条件下分别按照传统人工势场法和搭载改进人工势场法计算出的全局飞行路径,图6(b)则是在碰撞威胁物附件路径的放大图,图6(c)是无人机路径点与碰撞威胁物的距离情况统计,图6(d)是无人机行进路程点与目标集结点的距离统计。

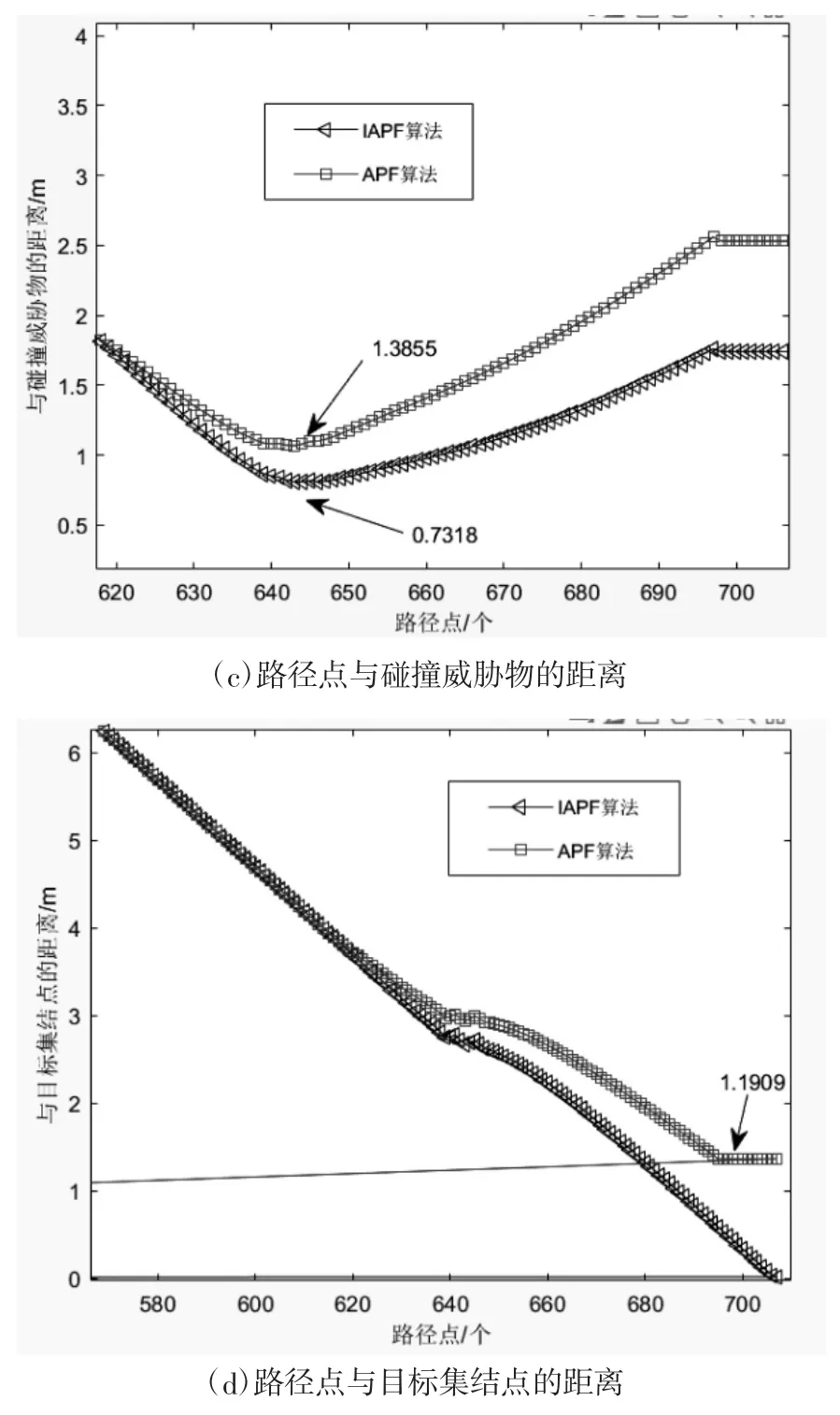
图6 路径振荡实验情况
由图6(a)和图6(b)可知,在实验开始阶段,距离障碍物和目标点较远的情况下,两种算法的路径曲线几乎一致,这是由于此时无人机受到的吸引力和排斥力大小方向基本相同,所以导致路径几乎重合。随着无人机的飞行,逐渐靠近障碍物和目标点,当无人机距离障碍物小于危险告警区域范围3m时,开始受到排斥力的作用,两种算法的路径点开始出现差别,当进入到障碍物3m范围时,会突然施加一个较大的且由障碍物指向无人机机身的斥力,在传统人工势场下的反映出现了较为明显的路径振荡现象,由于振荡问题的发生,最后并没有达到指定目的地,而改进后的人工势场算法,在识别到出现振荡现象的时候,进行了二次合力计算的改动,及时抑制了路径振荡问题,躲避障碍物的路径转角较为平缓,最终成功到达了目标位置。
在图6(c)和图6(d)中,当无人机来到路径振荡发生的路径点时,搭载改进人工势场算法有及时抑制振荡路径的持续,躲避障碍物的弧度较小,因此距离障碍物也较为接近,最近距离仅有0.731m,但此距离仍然大于碰撞距离0.3m,属于可接受范围。而传统的人工势场算法,无人机因不能及时抑制路径振荡问题而来回振荡,虽然最终以较大角度成功躲避了障碍物,但还是没有到达目标点,离最终的目标点仍然有1.19m的距离。
4.3 仿真实验结果总结
表2所示为对极小值实验和路径振荡实验的数据总结,当遇到极小值和路径振荡问题时,搭载改进人工势场算法能成功解决局部极小值问题和路径振荡,最终到达终点,但传统人工势场算法却不能到达最终目标点,任务失败。IAPF算法距离障碍物的距离虽然仅为0.538m,相比于APF算法小,但也在可控范围,能够保障机身安全。

表2 仿真实验结果
5 结论
本文从无人机集群实际工作环境出发,首先对复杂环境下无人机集群通信稳定难以维持的问题,利用无线紫外光通信背景噪声小抗干扰能力强等优势,将其作为无人机集群的通信手段来应对不同距离的邻近无人机,在保障无人机运行期间通信稳定的情况下减少机与机之间动态变化下的撞击事件。接着对于现实中经常出现的局部极小值和路径振荡现象进行处理,并通过改进人工势场法有效解决了问题,进行了相关的仿真实验,实验现象表明,搭载无线紫外通信和改进人工势场的无人机,不仅能在复杂多变的环境下保持通信,有效预防机与机之间动态变化下撞机事件的发生,对于局部极小值和路径振荡问题也能很好地解决,使无人机能够在稳定通信的情况下,还能完成动态静态障碍物避障任务,成功到达目标位置。
