基于新型部分积生成器和提前压缩器的乘法器设计

蔡永祺，李振涛，万江华,

（1.湘潭大学物理与光电工程学院，湖南湘潭411100；2.湖南毂梁微电子有限公司，长沙410000）

1 引言

2 Booth 编码器

在通用微处理器中，乘法是通过时钟控制一连串的“移位-加法”操作实现，将乘数的每一位分别与被乘数相乘得到部分积，再将所有部分积进行压缩求和[1]。对于需要做大量卷积运算的数字信号处理器，多次“移位-加法”操作会造成芯片资源浪费，所以需要设计专用乘法器提高乘法运算性能[2]。专用乘法器需要在1 个时钟周期内对2 个bit 位的输入作快速并行乘法，同时由输入输出寄存器锁存数据，配合流水线操作[3]。

由Booth 夫妇提出的Booth 算法[4]是目前最流行的优化乘法器的算法，其编码思想开启了乘法器部分积阵列产生模块研究史的新纪元。华莱士提出的用多个保留进位加法器组成的华莱士树[5]也是目前流行的部分积压缩求和结构。文献[6]中提出一种部分积符号位扩展方法，能够有效解决部分积压缩求和时位数扩展带来的面积浪费，减少了压缩求和过程中大量的符号位运算，但部分积的符号位仍有冗余。文献[7]提出用2 个3-2 压缩器组成1 个4-2 压缩器来缓解传统压缩器处理位数不够的问题，但在部分积压缩求和时会造成资源浪费。文献[8]提出了一种Booth 选择器，其输入信号的产生过程复杂，正逻辑门数多，延时较大。

为了能让Booth 编码乘法器具有更快的速度和更小的面积，本文在上述已有的一些算法及结构的基础上，提出了一种新的Booth 编码器及部分积生成器，并通过简化逻辑，将部分积结果在进入压缩结构前进行处理，设计得到部分积提前压缩结构，最终搭建了一个16 bit 有符号数乘法器。

Booth 编码是一种常用的优化乘法器的方法，其基本原理是通过减少部分积的数量来简化运算，典型的Booth 编码算法有基2 Booth 编码、基4 Booth 编码和基8 Booth 编码算法。基2 Booth 编码算法编码表简单，算法容易实现，但不能简化运算；基8 Booth 编码算法可以减少3/4 的部分积，但编码中有乘-3 的操作，电路难以实现；基4 Booth 编码算法[7]可以减少一半的部分积，并且电路容易实现。本文基于基4 Booth编码算法设计Booth 编码器，以优化乘法器性能。

在乘法运算中，乘数为B，被乘数为A，B 在处理器中以补码的形式存在，基4 Booth 编码算法是通过在乘数B 末尾添一位0 充当B-1，n bit 数B 和A×B为

对-2B2i+1+B2i+B2i-1进行基4 Booth 编码，即可将A×B的部分积数量降低到B 位数的一半，节省逻辑单元的使用。由式(2)可知，-2B2i+1+B2i+B2i-1有0、1、2、-1、-2 这5 种可能的结果，A×B 的部分积有0、A、2A、-A、-2A这5 种结果。设计Booth 编码器，对每组-2B2i+1+B2i+B2i-1进行基4 Booth 编码，编码结果如表1 所示，编码结果分别为S、Sbar、Sel1、Sel2、E0。S 为补偿位[6]，在进行乘负数运算时，需要对被乘数进行求补码操作，S 用来实现求补码的加1 操作以及控制被乘数是否需要取反；Sbar为S 的取反，Sel1、Sel2代表被乘数是进行乘1 还是乘2 的操作，都为0 时被乘数进行乘0 操作；E0在被乘数进行乘0 操作时起作用，同时作用于符号位扩展。

表1 基4 Booth 编码结果

基4 Booth 编码电路如图1 所示，该电路实现了对乘数B 的编码，电路输入信号Ba、Bb、Bc为乘数的连续3 bit，输出5 个编码信号S、Sbar、Sel1、Sel2、E0。目前芯片设计多用CMOS 电路，CMOS 为反逻辑输出，所以该电路全用反逻辑门来实现，以减少编码电路延时。

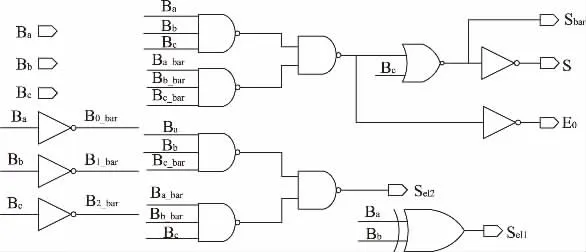
图1 基4 Booth 编码电路

3 新型部分积生成器

文献[8]提出的Booth 选择器结构如图2 所示，该电路有8 个输入，pp0[t]～pp3[t]为4 个部分积第t 位的可能值，需要对被乘数进行额外的计算方可得到该值；Sel0～Sel3是对乘数进行Booth 编码的结果，分别为A、2A、-A、-2A、0 的选择信号，用来选择正确的部分积可能值。该电路的被乘数需进行额外的计算，耗费大量面积，且使用大量正逻辑单元，增加了路径延时。

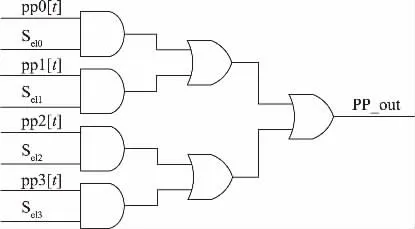
图2 文献[8]的Booth 选择器

针对上述Booth 选择器所带来的问题，本文提供了一种新的部分积生成方案，一次性完成部分积可能值的生成和部分积的选择。新型部分积生成器的电路如图3 所示，它共有7 个输入和2 个输出，S、Sbar、Sel1、Sel2是由Booth 编码电路产生的，Ai为被乘数的某一位，Aibar为Ai的反信号，M 为上一个部分积生成器所输出的Mout。输出Pi+1为部分积P 第i+1 位的结果，因为部分积最低位P0为补偿位，所以部分积生成器针对第i 位被乘数所生成的是第i+1 位部分积。Mout则将Ai生成的部分积可能值提供给下一个部分积生成器进行选择。

图3 新型部分积生成器的电路

该部分积生成器由2 个与或非门组成，AOI1 中的与或逻辑利用S 和Sbar来选择Ai或Aibar，实现乘数为负数时的取反操作，然后利用非逻辑取反，产生部分积可能值Mout，提供给AOI2 进行选择的同时还输出给下一个部分积生成器；AOI2 实现基4 Booth 编码算法的乘2 操作，该门的与或逻辑通过Sel1和Sel2对2 个部分积可能值进行选择，Sel1为高电平时选择AOI1 产生的部分积可能值，Sel2为高电平时选择上一个部分积生成器输出的Mout，最后非逻辑进行取反，输出部分积Pi+1。

其中X 和Y 为

被乘数进行取反操作后输入到该电路结构。该结构使用2 个与或非门实现对部分积可能值的生成以及选择，利用CMOS 反逻辑通过2 次取反得到正确的值；相较于文献[8]中的Booth 选择器，该结构使用更少的逻辑单元实现更多的功能，优化了电路的延时和面积。

4 部分积提前压缩器

部分积低4 位P[3:0]如图4 所示，P0为补偿位S，需要与P1进行压缩求和。最常用的压缩结构是华莱士树[6]结构，压缩单元使用半加器、3-2 压缩器以及由2个3-2 压缩器所构成的4-2 压缩器。由图4 可知，后续压缩过程需用半加器压缩P1与P0，产生保留位S0与进位C1，后续将C1与P2进行压缩。

图4 部分积低4 位

S0和C1的表达式为

本文对式(6)(7)进行简化，设计了一种低位提前压缩器，在部分积生成时就将P1和P0进行压缩，通过低位提前压缩器生成的新P[1:0]为

为了消除被乘数进行乘0 操作时部分积生成器所产生的错误的1，式(9)中对E0进行了或操作，可以在后续压缩进位中依次消除部分积生成器产生的1。部分积的低位部分在生成时已经被压缩，生成和压缩同时进行，减少了逻辑门的使用，从而使乘法器面积和运算延时减小。低位提前压缩器电路如图5 所示，图中3 个逻辑门就能实现部分积低位的生成、压缩。部分积低位示例如图6 所示，图中C1即P0，在后续过程中将与P2进行压缩、求和。

图5 低位提前压缩器电路

图6 本设计部分积低位示例

在所有部分积生成后进行压缩求和操作，每个部分积的位数对应的压缩权重不同，需要将所有部分积扩展至相同位数，文献[6]中的高位符号位扩展方法可以有效减少扩展操作以及压缩单元的使用。E 信号在部分积为正数时为高电平，扩展后的第1 个部分积的高3 位符号位P[19:17]即{E,E,E}，其他部分积的高2 位为{1,E}。第1 个部分积高3 位有很强的关联性，所以本文又提出了一种高位提前压缩器，利用其关联性，简化压缩步骤。

本文所设计的16 bit 有符号数乘法器经过Booth编码后共产生8 个部分积。将通过低位提前压缩器产生的第8 个部分积的C1与第8 个部分积的P2用半加器进行压缩，产生的进位为C2，正好与第1 个部分积的P17权重相同，可以在进入压缩树之前先将它们合并，由于第1 个部分积P[19:17]值只有{1,0,0}和{0,1,1}2 种，经过合并后不会产生进位，只会产生3 个保留位。高位提前压缩器将第1 个部分积低位所产生的C2与第8 个部分积的高3 位提前进行合并生成Pnew[19:17]，其逻辑表达式为

经过化简后只需要3 个逻辑门即可将4 个值进行合并，在提高效率的同时减少了压缩单元的使用，高位提前压缩器的电路结构如图7 所示。

图7 高位提前压缩器的电路结构

5 乘法器结构

将基4 Booth 编码器、新型部分积生成器、部分积提前压缩器运用至16 bit 有符号数乘法器，该乘法器经过基4 Booth 编码共生成8 个部分积，单个部分积生成流程如图8 所示。图中的Ba、Bb、Bc进入Booth 编码单元进行编码，A 的最低位A0与编码结果通过低位部分积提前压缩单元生成部分积P 的低2 位P[1:0]，被乘数高15 位A[15:1]与编码结果通过新型部分积生成单元生成部分积P[16:2]，并产生进位信号，进位信号与编码结果通过高位符号位扩展单元完成对部分积的符号位扩展，从而生成整个部分积结果。

图8 单个部分积生成流程

8 个部分积PP1～PP8 全部生成后，使用华莱士压缩树结构对其进行压缩求和，乘法器压缩求和流程如图9 所示。将8 个部分积分为2 组，PP1～PP4 为第1组，PP5～PP8 为第2 组，使用4-2 压缩器进行压缩[7]，PP1 的高位符号位和PP8 的C2进位通过部分积高位提前压缩单元压缩后再参与到第1 组4-2 压缩器。2组4-2 压缩器出来的结果进入到第2 级4-2 压缩器，最后用加法器进行求和，加法器的输出即为乘法最终结果。

图9 乘法器压缩求和流程

6 验证与综合

本文使用电路设计工具进行16 bit 有符号数乘法器的电路搭建，导出CDL 网表，通过脚本语言将CDL网表转换成门电路级别的Verilog 代码。用Verilog 描写测试文件，输入随机的16 bit 有符号数x、w 作为乘数和被乘数，输出定义为y_latch。然后给定一个乘法结果原型y_real=x×w，y_latch 和y_real 结果相同时赋予check 为高电平，其他情况为低电平。使用Verilog仿真工具进行仿真，波形如图10 所示，图中的check 信号为高电平，说明计算出来的结果与原型相同，证明本文设计的16 bit 有符号数乘法器计算功能正确。

图10 乘法器仿真波形

使用逻辑综合工具在28 nm 工艺下对其进行综合，本文中Verilog 代码是使用门电路搭建的，所以使用逻辑综合工具对设计进行唯一化处理，确保了乘法器数据的真实性。由综合报告可知，乘法器的关键路径延时为0.77 ns，时钟频率可达到1.3 GHz，总逻辑单元数为894 个，总面积为937.3 μm2，功耗为935.71 μW。本设计与文献[8]提出的Booth 选择器的参数对比如表2 所示，本设计与相似类型乘法器参数对比如表3所示。从对比结果可知，本设计在延时、总面积方面都有较大的优势。

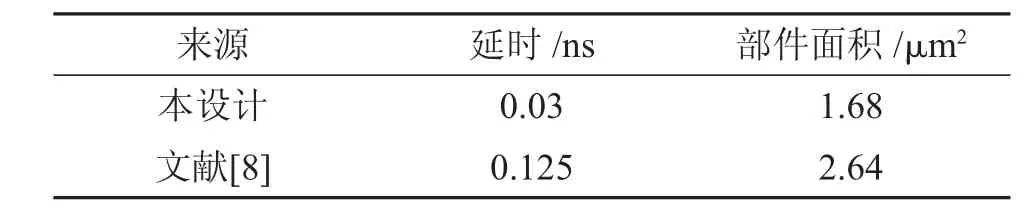
表2 本设计与文献[8]提出的Booth 选择器的参数对比

表3 本设计与相似类型乘法器参数对比

7 结论

本文设计了一种新型16 bit 有符号数乘法器，使用基4 Booth 编码，减少了一半的部分积；设计的新型部分积生成器结构简单，在节省逻辑单元的同时拥有更低的延时；设计了新型低位部分积提前压缩器，将8个部分积的低2 位在生成时就进行压缩；设计了高位部分积提前压缩器，将第8 个部分积的高位符号位先进行合并处理，再进入压缩结构，低位与高位的提前压缩器设计优化了压缩逻辑，减少了压缩单元的使用。与文献[8]相比，本文设计的乘法器关键路径延时降低了21.4%，总面积减少了49.6%，计算性能大大提高，该乘法器的实现思路可以很好地适用于现代乘法器。