秦岭林区红桦天然林直径分布建模与差异分析

牛永红,孙帅超,黄宏超,陈书军,曹田健*

(1.西北农林科技大学 林学院,陕西 杨陵 712100;2.生态仿真优化实验室,陕西 杨陵 712100;3.福建农林大学 林学院,福建 福州 350002;4.中国林业科学研究院资源信息研究所 国家林业和草原局森林经营与生长模拟重点实验室,北京 100091)

红桦(Betulaalbosinensis)是中国特有树种,其生长快,根系发达,在秦岭林区发挥着水源涵养、维持区域生态平衡等重要生态功能,是秦岭植被垂直带谱的重要组成部分[1]。目前对于红桦的研究已有许多,陈怀祥[2]研究了间伐对红桦各径阶林木生长状况的影响,林玥等[3]、缪宁等[4]以直径结构代替龄级分析了红桦的种群结构和空间分布格局,郭垚鑫等[1]、范得芳[5]利用直径结构划分发育阶段以分析红桦的群落稳定性及群落演变趋势。王连贺[6]利用林分结构因子和空间结构参数分析后发现,秦岭南坡红桦林树种空间大小分化差异明显,大部分树种属于劣汰木。因此如何更深入地了解林分结构,建立合适的直径分布模型对研究秦岭红桦天然次生林的生长经营至关重要。

林分直径分布,是林分内各种大小直径的林木按径阶的分配状态,是林分结构中最基本的一类结构[7],可以作为林分结构的表示,解释林分的未来生长潜力[4]。直径分布的形成原因取决于林木个体的生长差异,同时还受树种生长习性、环境条件和经营活动等因素影响[8-10],是控制林分密度和树种组成的重要指标。直径分布常借用一些理论分布函数来表征,包括正态分布、对数正态分布[11]、指数分布、Beta分布[12]、Gamma分布[13]、Weibull分布[14]和Johnson'SB分布[15]等。其中,Weibull分布因其形式简洁,易于计算参数和极佳的灵活性而被广泛用于研究林分直径分布[16],如火炬松(Pinustaeda)[17]、蒙古栎(Quercusmongolica)[18]、桤木(Alnusglutinosa)[19]以及松栎混交林[20]等不同树种和森林类型中。

Weibull函数的参数估计常使用参数预估法(PPM)和参数回收法(PRM),参数预估法从林分特征估计参数;参数回收法包括矩估计法和百分位估计法,分别从直径分布的矩和百分位数估计参数。结合不同模型拟合方法如最小二乘法(OLS)、极大似然法(MLE)、累积分布函数法(CDF)等拟合基于林分变量建立的关于Weibull 参数、矩或百分位数的回归方程[16]。在不同林分中的研究发现,参数估计法和模型拟合法的选择对于直径分布拟合效果有所差异:Ciceu等[21]认为基于矩估计法的PRM在参数估计表现上优于PPM;Cao[17]建立的CDF在估计火炬松直径分布中表现优于传统的OLS和MLE。Poudel和Cao[16]在CDF基础上后续提出了修正的累积分布函数法(MCDF),并得到了极佳的估计效果,但Schmidt等[22]在大桉(Eucalyptusgrandis)的研究显示MCDF法表现最差。因此,有必要根据不同林分类型选择合适的直径分布建模方法以提高对林分直径分布的估计精度,更细致地展示林分直径分布的变化趋势,探明造成林分直径分布的因素。

天然林林分状况复杂,影响直径分布的因素往往与林分内多个调控机制相关联[10],且随林分发育程度增加,直径分布也呈现出极大的异质性[23]。为探明秦岭红桦天然次生林直径分布规律,本研究基于秦岭林区181块红桦样地数据,拟解决以下研究问题:1)构建红桦天然林直径分布模型; 2)分析红桦天然林直径分布的差异。

1 研究区概况

研究区域设置在陕西省秦岭南坡中段的旬阳坝林区(103°58′-109°48′E ,32°29′-33°13′N)、火地塘林区(108°21′-108°39′E ,33°18′-33°28′N)以及黄柏塬林区(108°16′-108°86′E ,33°42′-33°50′N)。林区内地形复杂,坡度20°～35°,海拔1 600～3 071 m,土壤主要为山地棕色森林土,土层平均厚度约为50 cm。该区属于北亚热带气候类型,年平均气温9～10.5 ℃,年均降水总量915～1 050 mm,且集中于7-9月,年均湿度约77%,植物生长期6个月,平均无霜期199 d。区内多为天然次生林,森林类型属典型山地温带落叶阔叶林,主要成林树种为油松(Pinustabuliformis)、华山松(Pinusarmandii)、锐齿槲栎(Quercusalienavar.acutiserrata)、红桦(Betulaalbosinensis)、巴山冷杉(Abiesfargesii)、铁杉(Tsugachinensis)等。

2 材料与方法

2.1 样地数据

本研究采用样地数据来自于秦岭南坡的旬阳坝林区、火地塘林区和黄柏塬林区中立地条件相近,具有成片红桦分布的林分,包括2012-2013年设置的84块20 m×30 m调查样地[24],2013-2015年设置的66块[25]以及2021年设置的31块,共计181块红桦样地。样地调查内容包括树种、胸径、树高、枝下高、冠幅、优势木树高等林分调查因子信息,优势木按照1株/100 m2最高树选定。表1概括了各林区自然及林分调查因子。林区间海拔和气候差异较小,具有相似的自然条件,土壤为棕色森林土,厚度为50 cm左右[24]。林分调查因子方面,差异主要体现在平均直径(Dq)和林分密度(N)上,旬阳坝林区具有最小的平均直径和最高的林分密度(Dq=15.3 cm,N=1 072 株/hm2),而黄柏塬林区则具有最大的平均直径和最低的林分密度(Dq=20.4 cm,N=591 株/hm2),火地塘林区处于二者之间(Dq=18.3 cm,N=804 tress/hm2)。

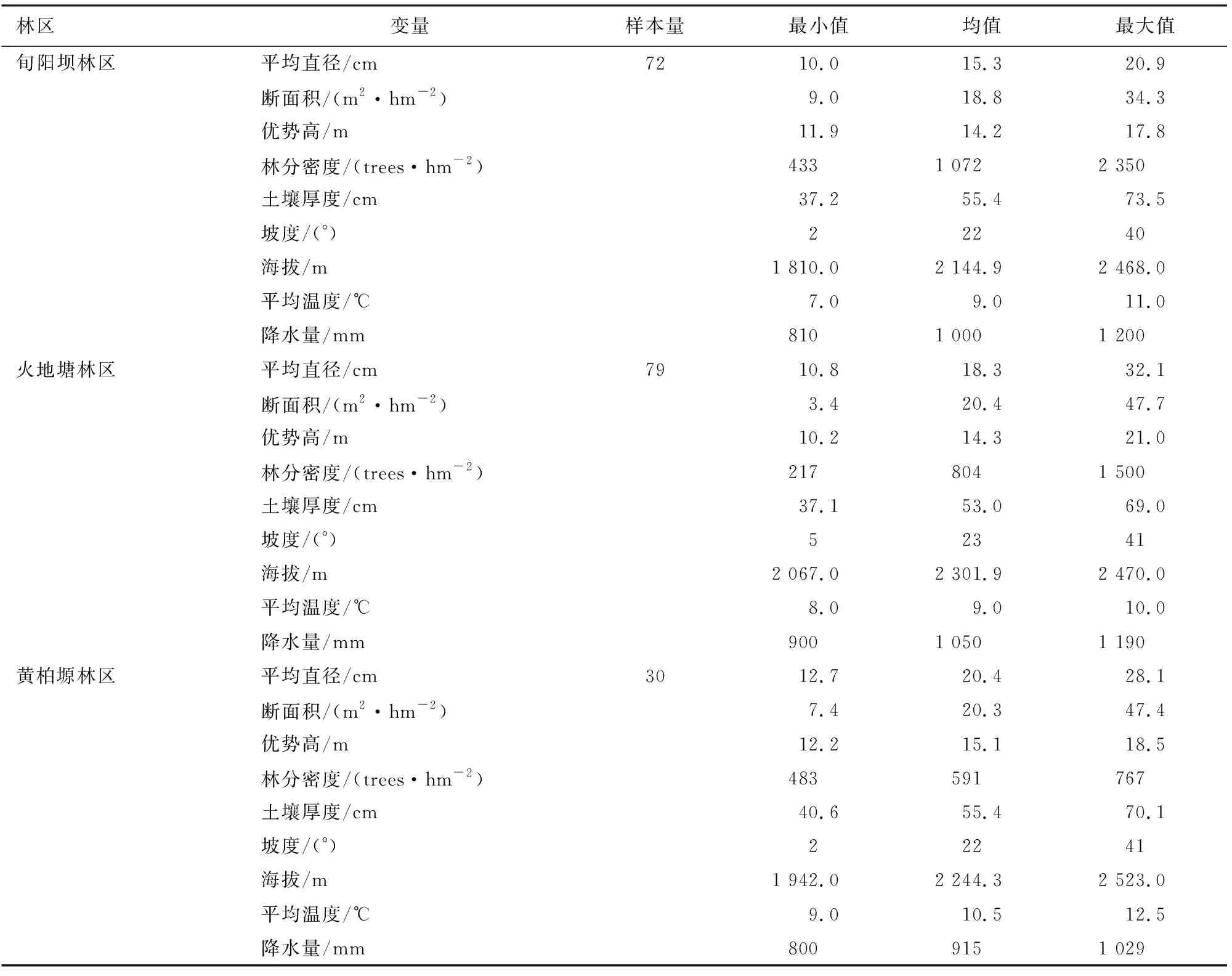
表1 各林区概况

2.2 直径分布模型的建立

2.2.1 分布函数的选择 本研究采用三参数Weibull函数来构建直径分布模型,其概率密度函数f(x)为

f(x)=

(1)

式中:x代表单木胸径实测值;γ1为位置参数,本研究根据起测胸径设置为5 cm;γ2为尺度参数;γ3为形状参数。

2.2.2 Weibull参数的预测 本研究采用矩估计法和混合估计法对Weibull参数进行预测,并对比不同参数预测法的性能。用来预测Weibull参数和直径的“矩”的回归方程如下

(2)

(3)

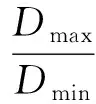
在矩估计法中,Weibull参数γ2和γ3由Dq和Dvar2个“矩“回收得到,其中Dvar由式(2)估计所得,后联立式(4)、式(5)获得参数γ2和γ3

(4)

(5)

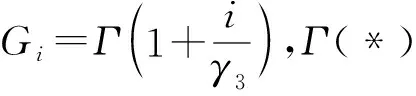
混合估计法则同时结合了参数预估法与参数回收法,形状参数γ3由式(3)计算得到,尺度参数γ2则基于参数γ3和林分平均直径Dq,利用式(4)计算获得。

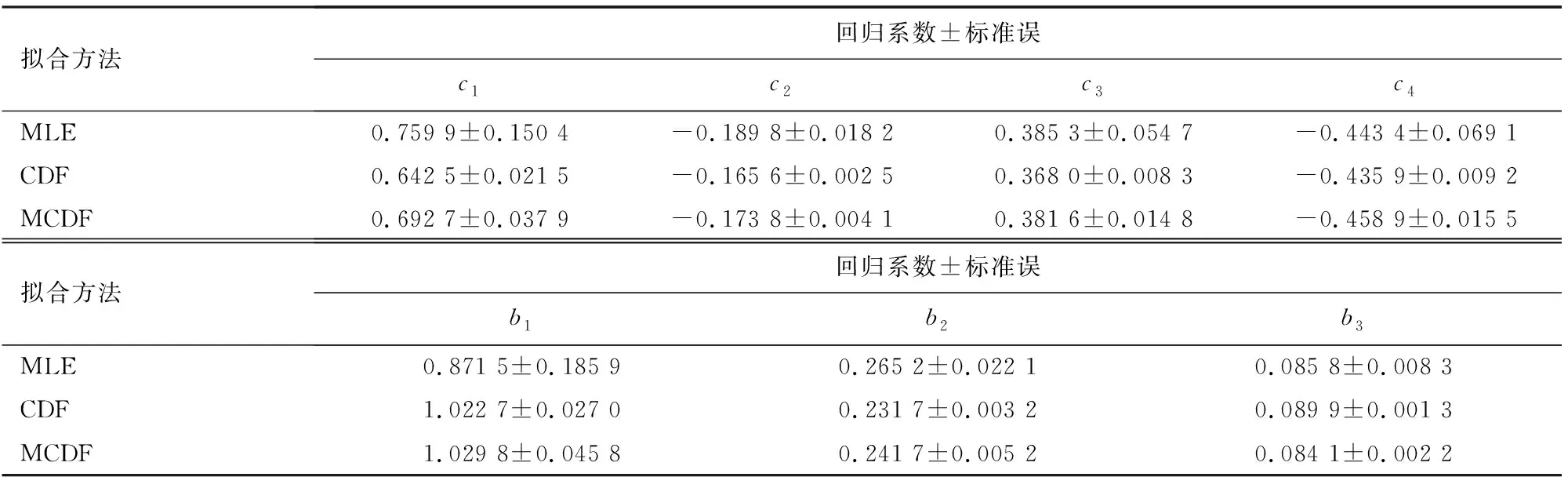
2.2.3 直径分布模型的拟合 本研究基于SAS软件中NLIN程序,采用极大似然估计法(MLE)、累计分布函数法(CDF)、修正的累计函数分布法(MCDF)对式(2)、式(3)的系数进行拟合,运行代码参考Sun等[20]为秦岭林区松栎林建立的直径分布模型。

极大似然估计法估计精度高,是最常用的模型参数估计法之一,通过极大化样地对数似然函数值之和,实现对模型回归系数的估计。目标函数为

(6)

式中:mi为第i个样地的林木株数;k为样地数;lnLi是第i个样地的对数似然函数。

累计分布函数法通过极小化每株林木的累计分布概率的实测值与预测值的平方差之和,实现对模型回归系数的估计。目标函数为

(7)

(8)

(9)

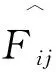
修正的累积分布函数法在累积分布函数法的基础上将每株林木进行2 cm径阶划分,使得每个径阶上界值的累计分布概率的实测值与预测值的平方差之和极小化。目标函数为

(10)

(11)

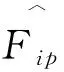
2.3 检验与评价

使用二折交叉验证,计算Anderson-Darling(AD,式中用AD表示)统计量、Kolmogorov-Smirnov(KS,式中用KS表示)检验值和负对数似然(-lnL)统计量指标,对建立的直径分布模型拟合精度和预测效果进行评价检验。各误差统计量指标数学表达式如下

ADi=-mi-

(12)

(13)

(14)

式中:uj=1-exp[-((DBHij-γ1)/γ2)γ3];mi为第i个样地的林木株数;DBHij为样地中按升序排列的各林木直径;lnL为Weibull分布函数的对数似然函数值。

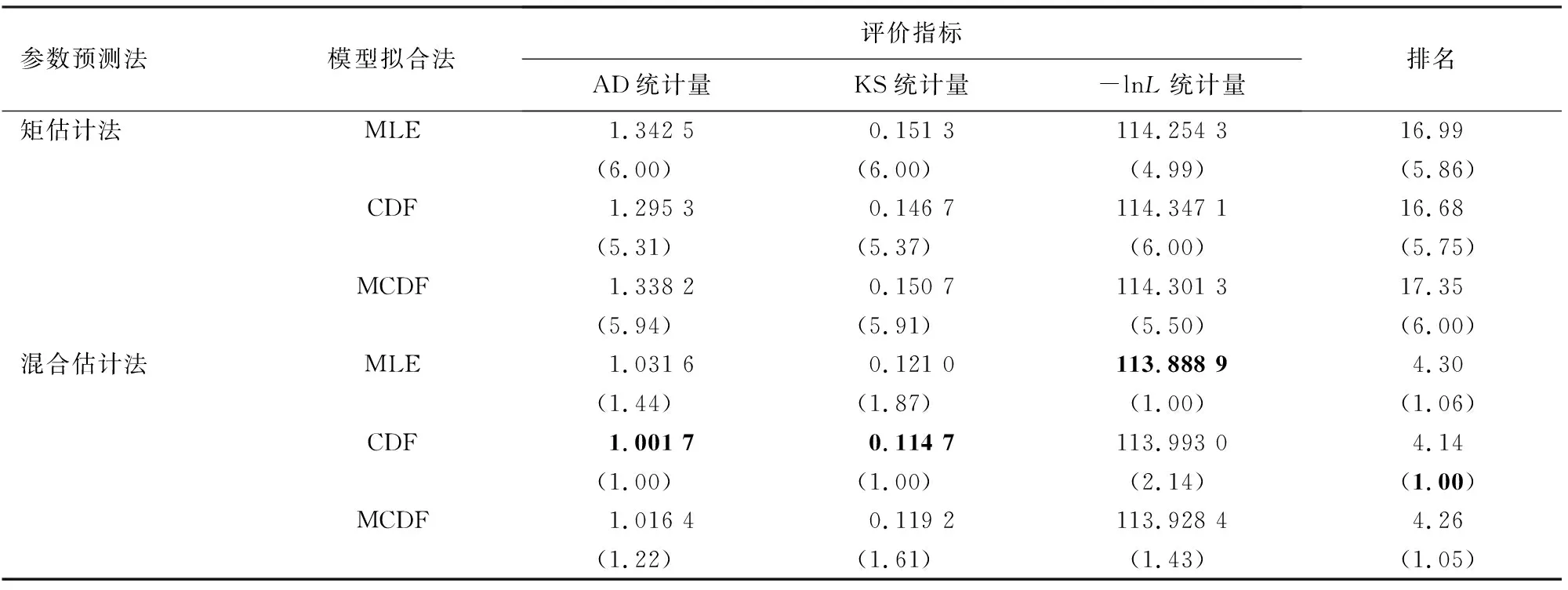
由于研究中采用了多种评价指标,不便于进行结果筛选。因此采用相对排名法获得所建直径分布模型的优劣顺序[16],采用式(15)计算不同误差统计量下的相对排名

(15)

式中:Ri为第i个方程的相对排名(i=1,2,…,e);e为评价的模型个数;Si为第i个模型的统计量值;Smax和Smin分别为Si的最大值和最小值。

Ri是介于1和e之间的数值,当Ri=1时,代表该直径分布模型表现最好,而Ri=e时,代表该模型表现最差。求得各模型在不同误差统计量下的相对排名后,根据相对排名之和得到最终评价排名,最终评价排名最高的直径分布模型为最佳直径分布模型。

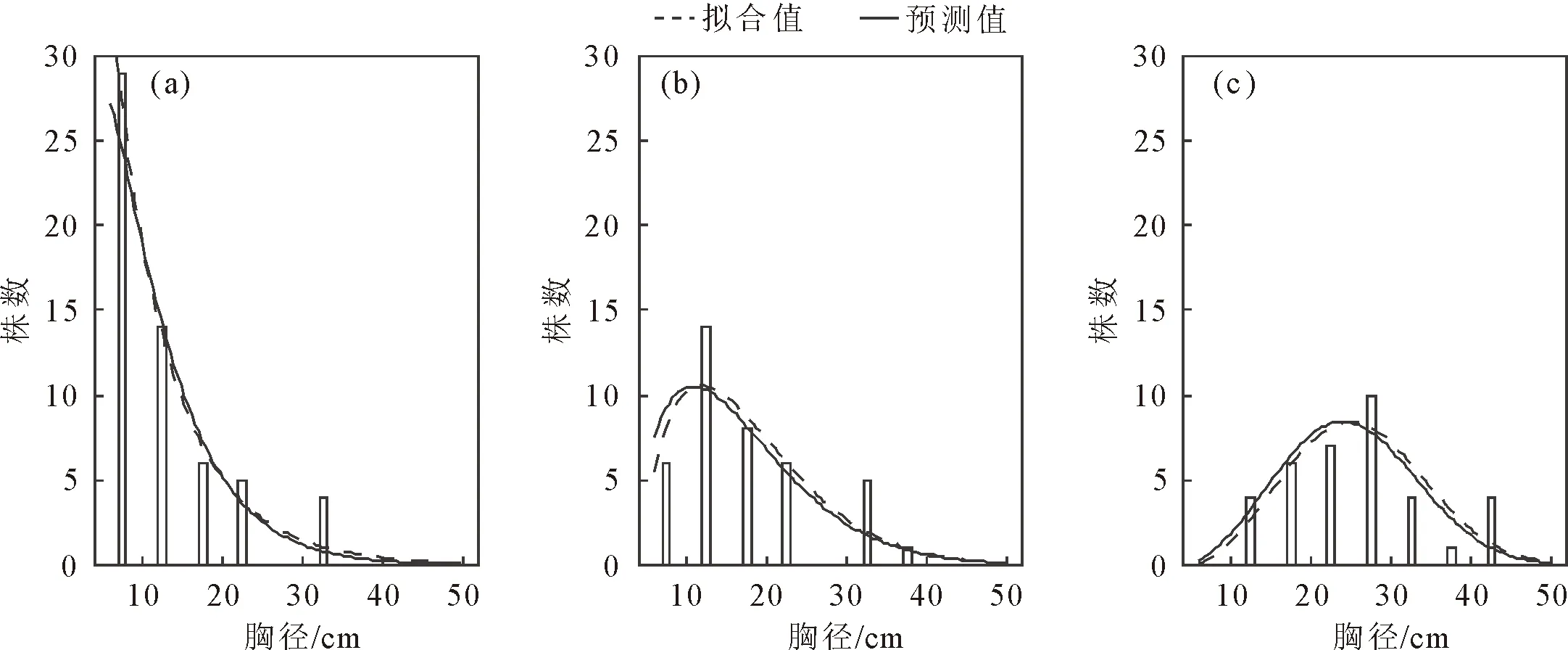
为验证模型预测效果,从各林区随机抽取1块样地,对比检验样地直径分布的Weibull函数拟合曲线与最佳直径分布模型的预测曲线。

2.4 影响红桦天然林直径分布差异的因素

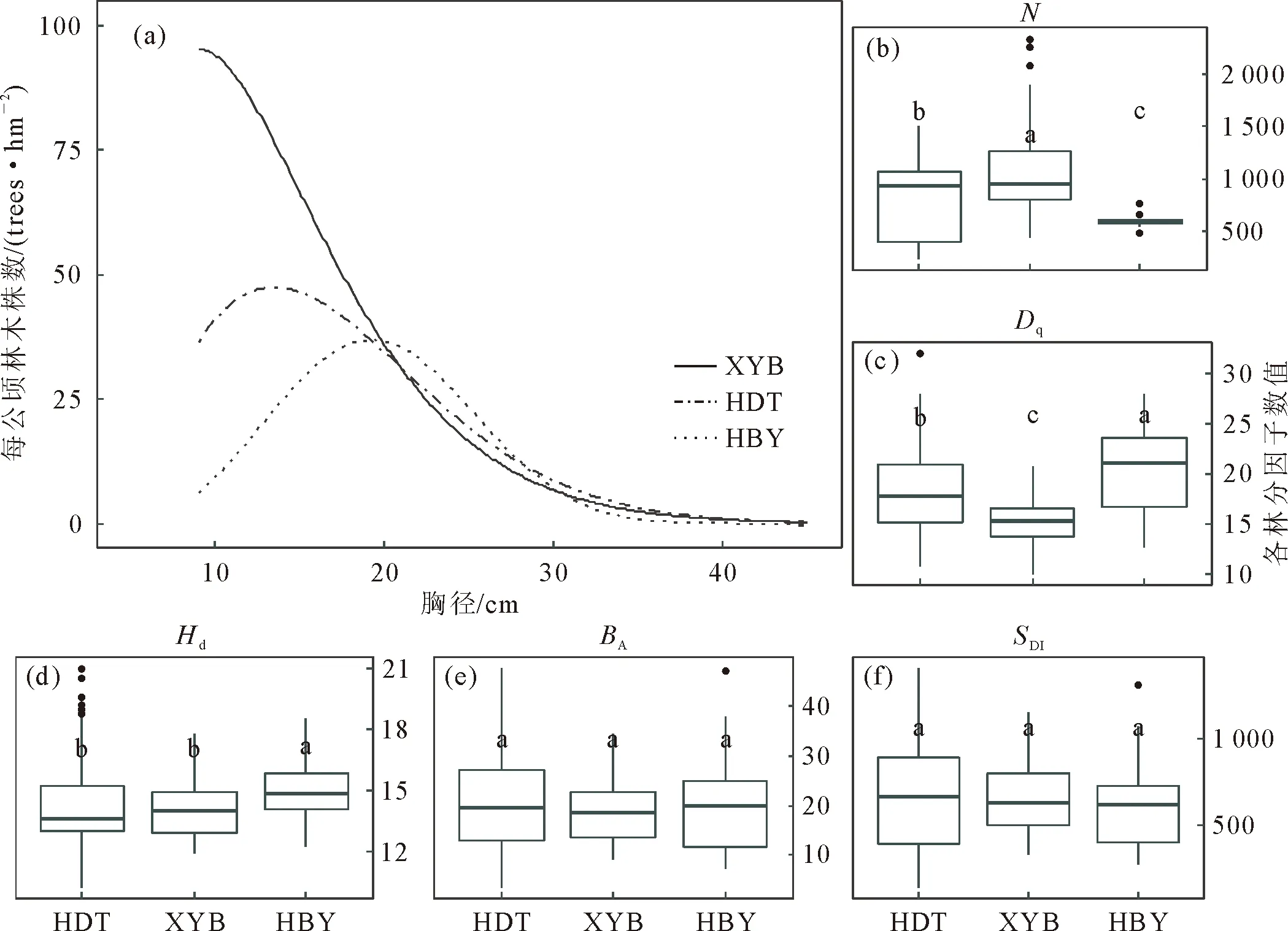
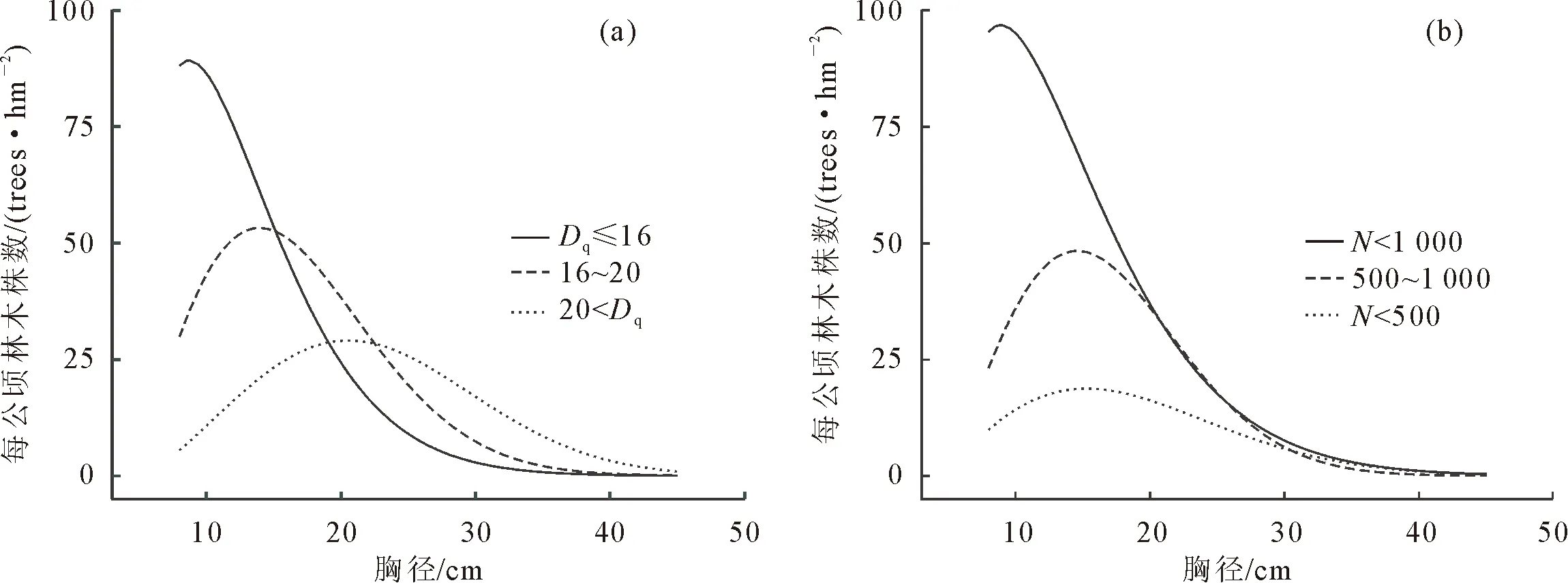
不同林区样地的林分条件各异,选择经Duncan检验后呈现显著差异的林分因子,利用所得直径分布模型进一步比较划分相关林分因子后直径分布曲线的差异,以探究造成红桦天然林直径分布差异的因素。分析样地数据范围,林分因子划分标准如下:基于林分平均直径(Dq)将样地划分为Dq≤16 cm、16 cm

3 结果与分析

3.1 不同林区的林分概况

对旬阳坝林区(XYB)、火地塘林区(HDT)和黄柏塬林区(HBY)的样地林分调查因子进行Duncan检验并利用Weibull分布函数拟合各林区平均样地的直径分布曲线(图1)。Duncan显著性检验结果显示,3个林区在林分株数与林分平均直径上存在显著差异(图1b、图1c)。林分株数上,旬阳坝林区(1 072±443 trees/hm2)显著高于火地塘林区(804±366 trees/hm2)高于黄柏塬林区(591±52 trees/hm2),但在林分平均直径上则相反,黄柏塬林区(20.4±4.6 cm)显著大于火地塘林区(18.3±4.3 cm)高于旬阳坝林区(15.3±2.3 cm)。在林分优势高方面(图1d),旬阳坝林区(14.2±1.6 m)与火地塘林区(14.3±2.3 m)的林分优势高无显著差异,但都显著低于黄柏塬林区(15.1±1.7 m)。然而,3个林区在林分断面积和林分密度指数上差异不显著(图1e、图1f),林分断面积依次为火地塘(20.4±9.7 m2)>黄柏塬(20.3±9.7 m2)>旬阳坝(18.8±6.1 m2),林分密度指数依次为火地塘(667±301 trees/hm2) >旬阳坝(667±209 trees/hm2)>黄柏塬(18.8±6.1 trees/hm2),这说明林区间林分整体竞争程度相似。林分因子间的异同使不同林区在直径分布上表现出明显差异,各林区平均样地的直径分布拟合曲线显示(图1a),旬阳坝林区(XYB)内存在较多胸径为10 cm的幼树,直径分布曲线近似于反J形;火地塘林区(HDT)幼树相对较少,林木株数主要集中于胸径10～20 cm,存在少量胸径为30 cm的红桦,呈现为正偏山状分布;黄柏塬林区(HBY) 10 cm以下的幼树较少,林区内多为20 cm以上的林木,近似于正态分布。

XYB为旬阳坝林区,HDT为火地塘林区,HBY为黄柏塬林区;N为林分密度(trees/hm2),Dq为平均直径/cm,Hd为优势高/m,BA为林分断面积(m2/hm2),SDI为林分密度指数箱线图上不同小写字母表示该因子在林区间差异显著(P<0.05)。

3.2 最佳直径分布模型的构建与检验

不同林区各样地的直径分布各异,针对181块红桦天然次生林样地的直径分布,筛选变量后得到回归方程(2)、方程(3),基于MLE、CDF和MCDF 3种模型拟合方法所得回归方程系数结果见表2。拟合结果表明,Weibull函数的形状参数γ3和林分中最大与最小胸径比值、林木密度负相关,和林分断面积正相关;林分中林木直径方差和林分中最大与最小胸径比值、林分平均直径皆正相关。此外,CDF拟合回归方程的各参数标准误平均为0.010 4,而MLE和MCDF各参数标准误平均分别为0.072 7和0.017 9,说明CDF拟合所得参数可靠性更高。

表2 不同拟合方法的回归方程系数值

利用交叉验证,计算所有样地在2种Weibull参数预测法和3种模型拟合法组合下各误差统计量均值,获得相对排名。根据相对排名进行最优直径分布模型的选择,模型综合评价结果见表3。对比2种参数预测法,矩估计法在各项误差统计量相对排名介于4.99～6.00,而混合估计法则介于1.00～2.14,基于混合估计法预测参数的直径分布模型总排名位列前三,相对排名之和为12.70,低于矩估计法排名之和51.01。对比3种模型拟合法,CDF表现最优,在不同参数预测法中相对排名均最高,相对排名之和为20.81;而MLE与MCDF总体表现差异较小,相对排名之和为21.29和21.60。因此,在对比各直径分布模型的不同统计量相对排名后,结果表明,混合估计法在Weibull参数预测上优于矩估计法,CDF在模型拟合上略优于MLE和MCDF,基于混合估计法预测参数,CDF拟合回归方程的直径分布模型相对排名最高。

表3 不同预测法和模型拟合方法组合下的统计量值

图2是从各林区中随机抽取3块样地的直径分布模型检验结果,结合混合估计法与CDF的直径分布模型能够较好地模拟反J形递减分布、正偏山状分布和正态分布等直径分布形态。模型对3块样地的预测结果与样地实际总株数平均相差3株,与拟合的直径分布曲线平均相差1株。以4 cm划分径阶后,模型预测结果与拟合的直径分布曲线在各径阶平均相差0.3株,与实际各径阶平均相差2株,且主要在7、11、15 cm等小径阶上误差较大,平均误差为3株。整体上看,模型对样地直径分布的预测曲线与直径分布拟合曲线在各径阶上偏差较小,但对个别径阶的实际株数估计效果欠佳。

(a)为旬阳坝林区3号样地:林分密度1 450 trees/hm2,平均直径12.1 cm;(b)为火地塘林区65号样地:林分密度1 100 trees/hm2,平均直径19.8 cm;(c)为黄柏塬林区165号样地:林分密度600 trees/hm2,平均直径27.1 cm。

3.3 影响林分直径分布的因素

选用上述研究中相对排名最高的基于混合估计法预测参数,CDF拟合回归方程的直径分布模型形式对划分林分因子后红桦天然林的直径分布进行拟合,获得不同林分因子下直径分布模型的参数值(表4)。

表4 不同平均直径和林分密度下红桦直径分布拟合结果

不同林分平均直径下的红桦林直径分布差异明显,平均直径在10～28 cm时,平均直径越大,分布曲线越左偏(图3b)。林分平均直径<16 cm时,林木株数主要集中在10 cm左右,直径结构近似反J形递减分布,而随着林分平均直径又不断增大,直径结构趋向正偏山状分布,当林分平均直径达到20 cm时,近似于正态分布,表现为小径阶林木大幅减少,胸径为20～25 cm的中径阶林木居多数,且径阶分布范围更宽,峰值降低。

Dq为平均直径(cm),N为林分密度(trees/hm2)。

不同林分密度下的红桦林直径分布差异明显,林分密度在200～2 300 trees/hm2时,林分密度越大,分布曲线越右偏(图3c)。各林分密度的红桦林径阶分布范围相似,差异主要体现在胸径为10～15 cm处的小径阶林木株数。林分密度在1 000 trees/hm2以上时,呈近似反J形递减分布,林木株数集中于10 cm左右的小径阶,在10 cm处的株数可达100株,是林分密度<500 trees/hm2林分的5倍。林分密度为500～1 000 trees/hm2与林分密度<500 trees/hm2时的直径分布曲线偏度相近,且均呈正偏山状分布,但在胸径为15 cm处的株数峰值上相差约2.6倍。

4 结论与讨论

4.1 直径分布建模方法

本研究对秦岭红桦林直径分布模型构建中,发现混合估计法较矩估计法在模型参数预测上表现更好,而累积分布函数法(CDF)在模型拟合上也优于极大似然估计法(MLE)和修正的累积分布函数法(MCDF),所得的直径分布模型取得了最高的相对排名。这与在其他林分研究中认为矩估计法往往是最佳选择的结果有所不同[16,21]。Sun等[20]在松栎混交林的直径分布研究中表明,尽管矩估计法在全林分水平表现最佳,但针对某一具体树种如锐齿槲栎而言,混合估计法则具有更好的性能。Gorgoso等[26]在毛桦(Betulapubescens)直径分布中也发现矩估计法不比百分位估计法效果更优。这或许意味着矩估计法在阔叶树的直径分布模型的参数预测上不占据优势,参数预测法在使用时应考虑适用树种不能一概而论。而百分位估计法虽然受到了一些研究者的青睐,但考虑到林木在林分中的地位会随时间发生改变[27],林木直径所处百分位不确定性较大,在进行长期预测林分直径分布时应谨慎考虑。

研究中采用的相对排名法对基于不同方法构建的直径分布模型误差统计量进行综合对比评价以选出最佳模型[17],但Bankston等[28]认为这种将多个误差统计指标汇总评价的方法或仅提供了一个不具备实际意义的排名,且会因误差统计量指标的选择而改变结果。因此,有必要提供各评价指标独立的排名对比,以便根据不同误差统计量或拟合优度指标的适用情景选择合适的方法构建直径分布模型,为科学地开展天然林经营提供理论依据和技术参数

4.2 影响林分直径分布的因素

利用所建立的直径分布模型,对不同平均直径和林分密度下红桦林的直径分布进行分析后发现,3个林区的平均样地的直径分布曲线受林分平均直径与林分密度影响较大(图1),在分布曲线上也表现出了一定相似性(图3a、3b)。林分平均直径代表了林木平均大小,与林分的发育阶段有关,而由于林分自然稀疏规律的存在,即生长在较高密度种群内的林木,由于竞争产生的密度抑制效应,林木个体会逐渐死亡[29]。这意味着随林分发育,林木大小增加,林分密度会相应降低。林分密度与林木大小是林内直径分布的关键变量,因此,自然稀疏规律通过调节平均直径与林分密度的关系作用于林分的直径分布,而影响自然稀疏的因素对林分直径分布也具有一致的效用。对于红桦的生产经营而言,可以适当增加森林干扰和人为干预[1],以调整林分结构发展方向,实现经营目标。

4.3 局限性

抚育间伐会对样地林分直径分布造成影响[30],旬阳坝林区部分样地曾于2012年经历过不同程度的下层伐[31],其直径分布曲线不同于林区内其他未间伐林分的反J形而是呈正偏山状分布,但该林区仍有足够数量未受严重人为干扰的样地数据用于构建直径分布模型,不影响本研究对红桦天然次生林直径分布的模型构建和影响因素分析结果。

此外,Bankston等[28]认为样地过小会影响对直径分布的估计精度,但鉴于在更大样地尺度条件下,直径分布的异质性会被掩盖,不同类型的分布曲线会相互平均[23]。因此,虽然用以建模的样地规格并不统一,多为20 m×20 m的矩形样地,但本研究认为小样地的直径分布对区域内林分因子差异的反应更为敏感,有助于探究影响直径分布的关键林分因子,而建模精度的缺失可以通过样地数量以弥补,并在更大尺度的红桦样地上对模型进一步验证调整。

需要注意的是,本研究仅考虑了将林分平均直径(Dq)和直径方差(Dvar)作为“矩”回收的形式[17],而根据所回收的“矩”和所构建的回归方程的不同模型会产生不同的性能表现[21,32],后续也应拓展其他直径分布的“矩”形式进行对比,同时还可嵌入增强回归算法进行变量筛选[33]或结合人工神经网络代替传统回归方程[34],利用机器学习方法提高直径分布模型的预测性能。

4.4 结论

本研究以秦岭林区红桦天然次生林为研究对象,基于Weibull分布函数,对矩估计法、混合估计法2种参数预测方法以及极大似然估计法(MLE)、累积分布函数法(CDF)、修正的累积分布函数法(MCDF)3种模型拟合方法在红桦天然林直径分布预测中的有效性进行评价。结果表明采用混合估计法预测模型参数并用CDF进行拟合的直径分布模型精度最高。林分密度和平均直径对秦岭林区红桦直径分布影响显著,平均直径越大、林分密度越小的红桦林分直径越接近正态分布,平均直径越小、林分密度越大的红桦林分直径则呈右偏或倒J形分布。