层流搅拌槽内柱状单颗粒运动特性的研究

2023-12-09李志鹏高正明

北京化工大学学报（自然科学版） 2023年5期

王超李志鹏高正明

(1.中石化(北京)化工研究院有限公司, 北京 100013;2.北京化工大学化学工程学院, 北京 100029)

引言

机械搅拌作为一种强化固液两相传质的重要手段,广泛地用于各种生产过程,如催化剂表面的非均相反应[1]、微生物罐中的发酵过程[2]、搅拌反应器内的结晶过程[3]等。固液搅拌的最低要求是使全部固体颗粒与液相充分接触,此时对应的搅拌转速称为临界悬浮转速Njs(单位为r/min)。该定义最早由Zwietering[4]提出。在此基础上,学者们针对多种搅拌体系建立了Njs的关联式,并评估了颗粒浓度[5]、液体黏度[6]、搅拌桨尺寸及安装位置[7]等不同参数对Njs的影响规律。

上述有关Njs的研究主要侧重于大量球形颗粒在搅拌槽内的宏观运动特性。在颗粒运动特性研究方面,Wang 等[8]在带有标准Rushton 涡轮的搅拌槽内对8 个球形颗粒的悬浮特性进行了分析,槽内流体流动状态为层流;结果表明,颗粒在各运动阶段参数(如轨迹和速度)的实验数据与模拟结果吻合良好,颗粒的悬浮过程受颗粒周围压力梯度力的影响。在过渡流搅拌槽中,张昆等[9]利用高速摄像技术对多种球形单颗粒的运动规律进行了研究,结合粒子图像测速技术直观地展现了不同条件下颗粒运动状态发生改变的过程,并认为流体的主体流动是引起颗粒悬浮的主要原因。

多数生产中的固体颗粒为非球形,其中具有代表性的是柱状纤维,该种形状颗粒常出现在生物发酵[10]、增强复合材料[11]、储能材料[12]等领域。在以木质纤维为原料的生物质转化中,多以釜内机械搅拌作为强化固液两相热质传递的手段[13]。在流体的裹挟作用下,搅拌槽内的柱状颗粒除了存在位移,还在空间上发生旋转。 Fan 等[14]在带有Rushton 涡轮的搅拌槽中研究了搅拌速度、纤维长径比和固含率对速度场和颗粒旋转方位的影响,发现在层流条件下,颗粒形状是引起颗粒速度和流体速度分布发生改变的重要原因。 Derksen[15]采用数值模拟方法研究了多种柱状颗粒的悬浮行为,结果表明长颗粒旋转方位趋于水平,而短颗粒的旋转是随机的。

目前,关于搅拌槽内非球形颗粒运动规律的研究还有待补充。在颗粒尺度上,充分认识单颗粒的运动行为,并将其规律用于宏观多相流流动中,对于改善固液悬浮效果、优化搅拌操作具有一定的指导意义。因此,本文对搅拌槽内柱状单颗粒的运动特性进行了研究,采用可视化技术量化了颗粒运动过程中的参数(如运动轨迹、速度、旋转角度等),并利用基于格子玻尔兹曼方法(lattice Boltzmann method,LBM)的直接数值模拟建立流固耦合,模拟结果与实验数据吻合良好,获得了颗粒周围的流场分布和压力分布。所得结果可为搅拌槽内非球形颗粒运动特性的研究提供参考,并作为生物质搅拌设备设计和操作的理论依据。

1 实验装置和方法

1.1 实验装置与物系

为减弱因槽壁折射而引起的图像失真、提高颗粒质心识别精度,所有实验均在透明的平底方形槽内进行,并采用圆盘桨产生稳定的径向流。实验装置的结构与尺寸见图1。槽体边长T=220 mm,液位高度H=T= 220 mm,圆盘直径D= 2R=T/2 =110 mm,桨盘离底高度C=T/4 =55 mm。笛卡尔直角坐标系原点(0, 0, 0)位于槽底中心位置,z轴与搅拌轴中心线重合。

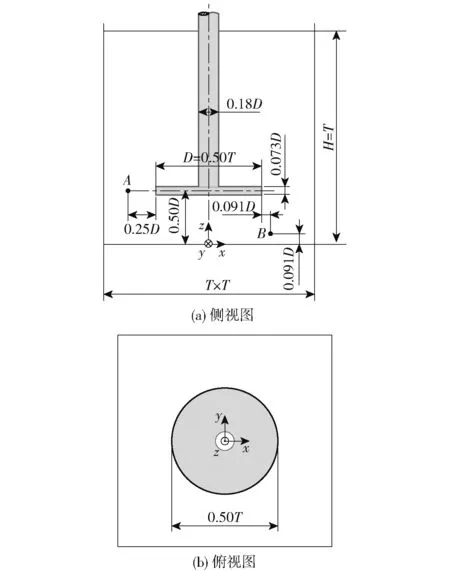
图1 实验装置的结构与尺寸Fig.1 Geometry and size of experimental equipment

以二甲基硅油(牌号为201-2000cst,上海树脂厂有限公司)为介质,密度ρ=965 kg/m3。靠近桨叶和槽底区域设置A、B 测温点,并利用MARS40 型旋转流变仪(德国哈克公司)测定硅油动力黏度μ。本文实验温度控制在(25.4 ±0.1) ℃,则μ为(1.90 ±0.004) Pa·s。

以聚四氟乙烯(polytetrafluoroethylene,PTFE)柱状颗粒为研究对象,密度ρp=2 210 kg/m3,直径dp=5.05、8.19、12.10 mm,长径比lp/dp范围为2 ～6,颗粒质心初始位置为(0, 0, 0.5dp)。为提升颗粒图像的识别精度,需降低搅拌体系的反光度,并增强图像对比度,因此在颗粒和搅拌桨/轴的表面均匀地喷涂了一层漆膜。

以搅拌雷诺数Re表征流体流动状态,以黏性Shields 数θ表示黏性力与净重力的相对大小,这两个无因次参数的计算公式如下。

式中,N为搅拌转速,r/min;g为重力加速度,m/s2;Sp为颗粒表面积,m2;Vp为颗粒体积,m3。

1.2 摄像系统与图像处理

图像采集系统如图2 所示。采用两台高速相机(丹麦丹迪动态公司)拍摄颗粒图像,并通过图像处理量化颗粒的运动过程。相机A 和B 分别置于槽侧面与底部,利用同步控制器完成A、B 相机的同步拍摄。以500 W LED 白灯作为系统光源,并使用半透明扩散板引导光源均匀地分布在整个拍摄区域内。 A、B 相机分辨率均为1 280 pixel ×1 024 pixel,帧率为100 fps,侧面与底部图像的解析率分别为0.15 mm/pixel 和0.14 mm/pixel。

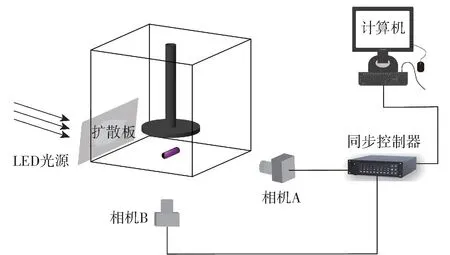
图2 图像采集系统Fig.2 Image collecting system

在Matlab(R2022a 版本)环境中处理相机捕获的图像,颗粒质心的识别过程如下:(1)通过数学形态学运算[16]预处理颗粒图像;(2)利用bwlabel 函数[17]寻找二值图像中的八连通域并连接这些区域;(3)使用regionprops 函数[18]度量上述八连通域的属性值,获得颗粒质心的像素坐标。

如图3 所示,定义颗粒方位角α和颗粒仰角β以量化颗粒旋转方位,其中α为x轴与颗粒长轴在x-y平面投影的夹角,°;β为颗粒长轴与x-y平面的夹角,°。具体计算如式(3)、(4)所示。

图3 柱状颗粒的方位角与仰角Fig.3 Azimuth angle α and elevation angle β of the cylinder

式中,i、j、k为颗粒质心坐标系中的单位向量。

2 数值模拟

2.1 格子玻尔兹曼方法

通过LBM 求解槽内流体的层流流动。 LBM 方法将流域离散为若干均匀的立方格,在一定时间步长内,处于立方格中心的流体粒子沿某个矢量方向迁移至邻近格子,并在格点发生碰撞,碰撞过程满足质量和动量守恒。通过求解玻尔兹曼输运方程,得到流体运动的宏观参数[19]。时间和空间分别用时间步长Δt和格子间距Δ表示。 LBM 涉及的物性参数具有“格子单位(lattice units,l.u.)”,根据网格解析率,可将带有“格子单位”参数等比例地转换为实际物理变量。

综上,格子演化过程可归纳如下。

1)流体粒子的迁移

2)流体粒子的碰撞(格子玻尔兹曼方程)

式中,Ni为流体粒子的质量密度;ci为第i个速度矢量;Ωi(N)为非线性碰撞算子,满足质量守恒和动量守恒

其中,fext为流体受到的外力。则流体运动的宏观参数可由式(9)、(10)计算。

式中,u为流体速度。

2.2 柱状颗粒的碰撞与受力

采用线性弹簧阻尼器模型(linear spring dashpot,LSD)[20]处理颗粒-壁面和颗粒-圆盘桨的碰撞。该模型将颗粒碰撞过程中产生的碰撞力Fc定义为弹性力Fel和阻尼力Fdamp的矢量和,其中弹性力和阻尼力又可分解为对应的法向力和切向力,Fc、Fel和Fdamp的单位均为N。

以颗粒-壁面碰撞为例,通过颗粒表面质点与槽内壁的间距,判断颗粒是否发生碰撞。当间距小于某个值时,向质点施加一个法向弹性力,防止颗粒与壁面重叠[21]。实验观察到柱状颗粒悬浮前会绕其长轴旋转,因此引入干摩擦力模型[20]处理作用于颗粒的滚动摩擦力。为增强接触力计算的收敛性,在LSD 模型中需设定阻尼力。对于球形颗粒,当颗粒与其他固体表面的间距小于Δ时,可采用亚格子润滑力模型求解间隙内的流体流动[22]。对于柱状颗粒,可借鉴球形颗粒的润滑力模型来解析两固体表面间的流体流动,从而实现阻尼作用[23]。

2.3 边界条件与流固耦合

为实现流体与壁面的无滑移条件,搅拌槽底部和侧壁采用半步长反弹格式[19],如图4(a)所示。槽内液面处为自由滑移边界,采用半步长镜面反射格式[24],如图4(b)所示。

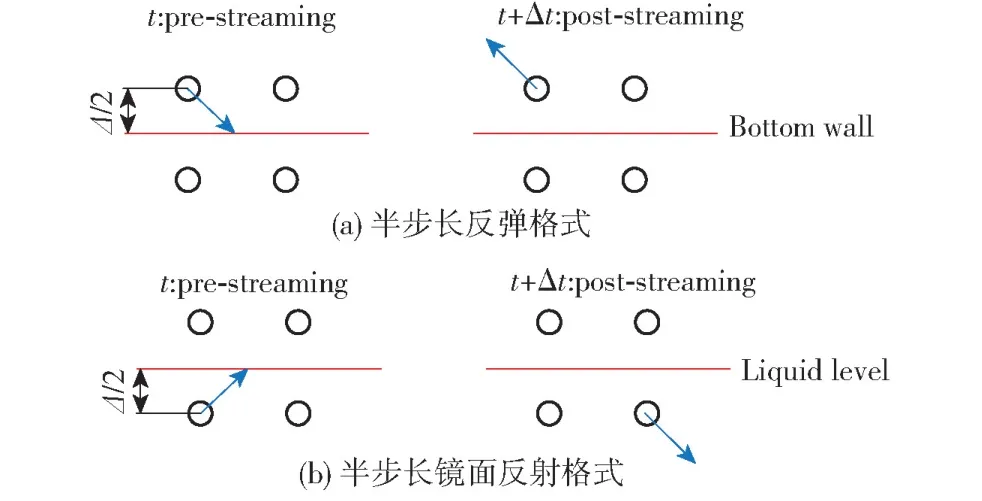
图4 两种半步长边界格式Fig.4 Two types of halfway boundary scheme

采用浸入边界法(immersed boundary method,IBM)处理运动物体的曲面边界[25]。以运动的柱状颗粒为例:在颗粒质心坐标系中,IBM 将颗粒表面离散成一群空间质点,根据质点与流体内插点间的速度差,对流体施加局部力以减小速度差异,由此实现无滑移条件,进而得到颗粒所受的水力学作用。颗粒表面质点完成流体受力传递后,结合颗粒净重力和碰撞力,求解颗粒线性运动方程(式(11))和旋转运动方程(式(12))[23],从而获得颗粒位置、位移速度和转动速度,由此实现流固耦合。

式中,up为颗粒质心速度,m/s;Fh为作用于颗粒的水力学力,N;ez为单位向量,其方向与颗粒重力方向一致;Ip为柱状颗粒转动惯量,kg·m2;ωp为颗粒角速度,rad/s;Th为作用于颗粒的水力学力矩,N·m;Tc为作用于颗粒的碰撞力矩,N·m。

2.4 四元数旋转矩阵

根据IBM 的处理方法,柱状颗粒所受水力学作用是由颗粒表面各质点的水力学力与力矩的矢量和求得,但颗粒表面的质点坐标是以柱状颗粒质心为参照系。为实现颗粒质心坐标系(xc,yc,zc)中的向量a与笛卡尔坐标系(x,y,z)中的向量b之间的转换,并解析颗粒的旋转过程,引入四元数旋转矩阵S[26]

式中,q0为四元数的实部;q1、q2和q3为四元数在3 个方向的虚部。

在模拟中,第m+1 次循环的四元数可表示为

式中,符号◦表示四元数乘法[27]。

3 结果与讨论

3.1 柱状颗粒的可视化运动与特性

柱状颗粒临界悬浮转速NLO(单位r/min)的确定过程如下:给定某个初始转速N0(单位r/min),使颗粒未悬浮;30 s 后,圆盘桨加速至某个转速N,若60 s 内颗粒未悬浮,停止实验;重复上述操作,每次将N增大2%,直至颗粒能在60 s 内悬浮,则该转速N定为NLO。其中,N0约为NLO的50%,各实验至少重复2 次。

临界条件下,3 种柱状颗粒的Re与lp/dp的关系如图5(a)所示。实验在相同温度和同种硅油中进行,则Re的变化可视为NLO的变化。当dp一定时,随lp/dp增大,Re最初有增大的趋势,这表明颗粒所受水力学力与其净重力正相关;当lp/dp＞4 或5时,Re的变化趋于平稳甚至下降,可推测出长颗粒周围的流场分布对其悬浮产生了影响。

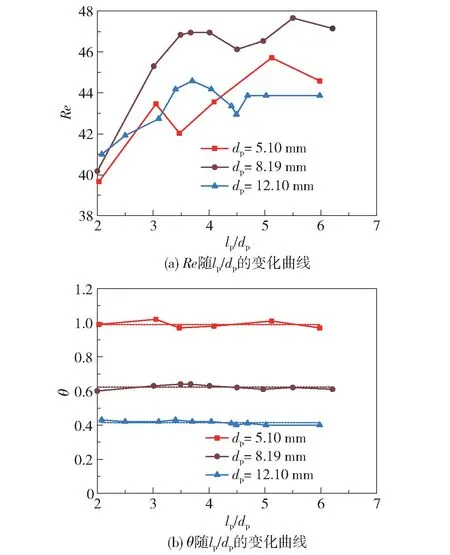
图5 颗粒悬浮的特征参数与颗粒尺寸的关系Fig.5 Relationship between suspension characteristic parameters and particle size

θ随lp/dp的变化如图5(b)所示。可以看出,对于同种直径的颗粒,θ几乎不随lp/dp的增大而发生明显改变。 Martino 等[28]的研究表明,柱状颗粒暴露于剪切流的截面面积对颗粒的初始运动产生影响。鉴于本文中的Re不超过50,流体流型为层流流动,则槽底附近的流体流动可近似为剪切流。根据θ的定义式,分母项为颗粒的净重力,分子项正比于颗粒受到的水力学力。图5(b)表明,随颗粒在流场中暴露面积的增大(或dp的增大),颗粒受到的流体水力学作用越强,离底悬浮所需的θ值越小。

根据颗粒运动状态的差异,将颗粒运动过程分为3 个阶段:①颗粒在流体的带动下于槽底中心区域发生微小移动;②颗粒某一端部离开槽底,其质心离底距离增大,逐渐上升至桨盘底部;③颗粒在桨盘底部区域运动,并由圆盘边缘甩入循环流区域。 1.2节所述的图像处理方法对于大颗粒能够取得较好的识别结果,因此后续仅讨论dp=12.10 mm 且lp/dp=2.08、3.10、4.04、5.98 柱状颗粒的运动特性。图6和图7 分别为dp=12.10 mm 且lp/dp=4.04 颗粒运动过程的实验图像和重复实验结果。在图6中,自桨盘开始加速,第一阶段耗时较长(约37 s),但仅需1 ～2 s 就可完成后续两个阶段。由图7 可知,颗粒在3 个阶段的运动参数具有良好的重复性,部分运动参数如下:①颗粒在槽底面的无因次运动轨迹(x/T和y/T);②无因次颗粒轴向质心位置(zp/C)随搅拌圈数(tN)的变化,其中zp为颗粒轴向质心位置,mm;③无因次颗粒上升速度(up,z/vtip)随搅拌圈数的变化,其中up,z为颗粒上升速度,m/s,vtip=πND为叶端线速度,m/s;④颗粒方位角(α)随无因次颗粒轴向质心位置(zp/C)的变化;⑤颗粒仰角(β)随无因次颗粒轴向质心位置(zp/C)的变化;⑥颗粒在桨盘底部区域的无因次运动轨迹(x/T和y/T)。定义颗粒在槽底的悬浮位置为颗粒质心轴向位置zp=1.0dp时刻,则颗粒悬浮位置(图7(a)中的星形符号)在两次实验中存在差异,这使得颗粒端部与圆盘桨底面的接触位置有所不同,如图7(f)所示,但颗粒仍有相同的运动趋势。桨盘的微弱晃动、颗粒与槽底之间表面粗糙度的随机性、颗粒形状不对称等因素可能是引起重复实验结果出现差异的原因。

图6 dp =12.10 mm 且lp/dp =4.04 颗粒运动过程的实验图像Fig.6 Experimental images of the motion process for the cylinder with dp =12.10 mm and lp/dp =4.04

图7 dp =12.10 mm 且lp/dp =4.04 颗粒的重复实验结果Fig.7 Results of two experiments for the cylinder with dp =12.10 mm and lp/dp =4.04

圆盘桨从转速为N0加速直至颗粒质心轴向位置达到zp=1.0dp过程中,颗粒在槽底的运动轨迹如图8(a)所示。在x-y平面上,不同颗粒的悬浮位置均不在槽底中心。无因次距离rb/T与lp/dp关系如图8(b)所示,其中rb为颗粒悬浮位置至(0, 0)点的距离,mm。由图8(b)可知rb/T与lp/dp线性正相关,即有rb/T=0.003 7(lp/dp) +0.009 1;拟合直线的截距大于0,表明即使颗粒长度较短,其悬浮位置仍会偏离槽底中心。

图8 dp =12.10 mm 颗粒在槽底中心区域的运动特性Fig.8 Motion characteristics of the cylinder with dp =12.10 mm moving over the center area of bottom wall

颗粒在离底悬浮阶段的运动特性如图9 所示。定义时间零点t=0 为颗粒质心轴向位置zp=1.0dp时刻,使用一阶导数的四阶中心差分公式计算颗粒上升速度和颗粒在桨盘底部的径向速度。

由于桨盘离底高度的限制(C=1/4T),lp/dp=4.04 和5.98 的长颗粒出现一端接触到桨盘底面、而另一端仍在槽底的情况,因此无因次轴向位置zp/C的最大值随lp/dp的增大而减小,且上升轨迹在tN=2.0 ～2.5 圈范围内的增幅趋于平缓(图9(a))。lp/dp=2.08 短颗粒能贴附于桨盘运动(zp/C=0.82),而lp/dp=3.10,4.04 和5.98 颗粒的zp/C最大值分别为0.75,0.74 和0.60,说明上述3 种颗粒与桨盘底部存在空隙,且空隙值与lp/dp正相关。

如图9(b)所示,颗粒上升速度up,z存在两个峰值。长颗粒(lp/dp=4.04 和5.98)的第一个峰值位于tN=1.28 圈,此时颗粒某一端接触槽底、另一端正悬浮上升;短颗粒(lp/dp=2.08 和3.10)在完全离开槽底面后,达到第一个峰值。在第二个峰值处,所有颗粒的运动状态均为一端触碰桨盘底面,并以该接触点为支点,另一端向桨盘底面旋转。

α变化360°表示颗粒从其初始位置旋转一圈。由图9(c)可知,旋转圈数随lp/dp的增大而减小。在图9(d)中,β随zp/C的增加先增后减,且在zp/C=0.46 处有最大值,该最大值与lp/dp负相关。当zp/C增至最大值时,β≈0,颗粒长轴平行于桨盘底面。

图10 为颗粒在桨盘底部区域的运动特性。在图10(a)中,首个数据点为颗粒一端与桨盘底部的碰撞瞬间。由于rb/T与lp/dp正相关,因此长颗粒的质心在桨盘底面的投影轨迹较短;对于lp/dp=2.08 的短颗粒,则随桨盘螺旋运动。由图10(b)可知,在同一无因次径向位置r/R处(其中r为柱状颗粒质心在桨盘底部投影的径向位置,mm;R为圆盘桨半径,mm),无因次颗粒径向速度up,xy/vtip随lp/dp的增大而减小;up,xy与叶端线速度vtip的差异随r/R的增大而增大,说明颗粒与桨盘间存在相对滑移,且滑移速度与lp/dp正相关。相比于其他颗粒,lp/dp=2.08 短颗粒的径向速度更接近于叶端线速度,说明lp/dp较小的颗粒的运动跟随性较好,与桨盘间的滑移速度较小。

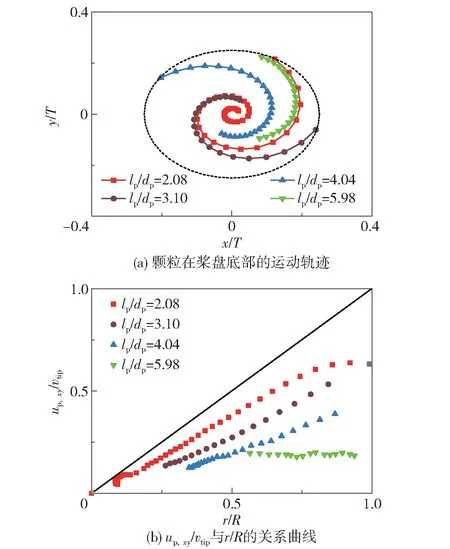
图10 dp =12.10 mm 颗粒在桨盘底部区域的运动特性Fig.10 Motion characteristics of the cylinder with dp =12.10 mm under the area of the disk

3.2 数值模拟结果

本文采用基于LBM 的直接数值模拟解析颗粒的运动过程。以lp/dp=4 的颗粒为例,考察网格解析率对模拟结果的影响。如图11 所示,分别取dp=6Δ、8Δ、12Δ和16Δ,则槽内流域网格数分别为1103、1473、2203和2943。模拟中的Re与实验结果相同。由图11 可知,在横轴取值相同的条件下,dp=6Δ的模拟结果相对于其余3 种解析率的结果存在差异,dp=6Δ下的上升轨迹、上升速度、方位角和仰角的最大相对平均偏差分别为1.62%、2.21%、3.32%和6.91%。为保证模拟精度并节约计算资源,确定网格解析率dp=12Δ。

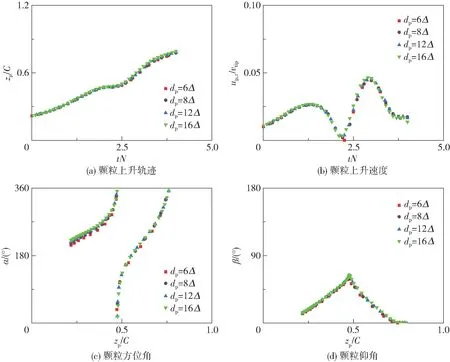
图11 lp/dp =4 柱状颗粒悬浮上升过程中,网格解析率对其运动和旋转方位的影响Fig.11 Effect of grid resolution on the motion and the orientation of the cylinder with lp/dp =4 during the lift-off process

zp/C=0.6dp时,槽内瞬态流场和压力分布如图12 所示。轴向流场与y=0 平面重叠,径向流场穿过颗粒质心且与z=0 平面平行,红色十字代表槽底中心位置。无因次压力标尺中,P为流体压力,Pa;P0为大气压,Pa。所用颗粒dp=12Δ,lp/dp=2、3、4 和6,且zp=0.6dp。由图12 可知,流场呈径向流特征,流动状态为层流(Re＜50)。远离槽底中心的流体流速较大,lp/dp=6 的长颗粒两端位于该区域,则颗粒受到的主体流动作用较强、悬浮所需的Re和θ较小。此外,径向方向的负压梯度减弱了颗粒表面水力学力分布的对称性,因此颗粒将偏离槽底中心悬浮。

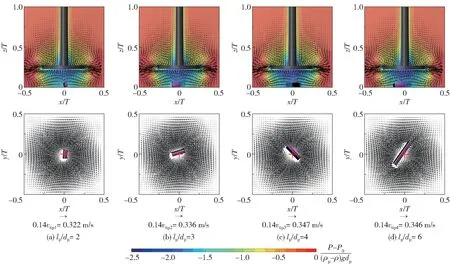
图12 搅拌槽内瞬态流场和压力分布Fig.12 Instantaneous flow field and pressure in the agitated tank

根据实验现象,以dp=12Δ且lp/dp=4 的颗粒作为典型示例,其运动特性的模拟结果与实验数据基本吻合(图13)。由图13(a)可知,颗粒悬浮位置的模拟结果与实验数据均偏离(0,0)点。由于颗粒与槽底间的表面粗糙度难以测量,且为了限制颗粒悬浮位置与(0,0)点的距离,模拟设定较大的切向弹性力和滑动摩擦力,因此运动轨迹的模拟结果较短。对于不含干摩擦力模型的结果,该条件下颗粒所受径向摩擦力较小,颗粒在相同时间步长内就能偏离(0,0)点而悬浮,则其运动轨迹较短、轨迹线的曲率半径较大。

图13 dp =12Δ 且lp/dp =4 颗粒运动特性的模拟结果与实验数据Fig.13 Simulated results and experimental data for the cylinder with dp =12Δ and lp/dp =4

颗粒悬浮上升阶段的对比结果如图13(b) ～(e)所示,可以看出颗粒上升速度up,z的模拟结果仍存在两个峰值。由颗粒悬浮过程中的流场和压力分布可知:(1)随颗粒某端部的上升,其上部和下部形成负压梯度,此压力梯度引起的力促使颗粒加速上升,如图14(a)所示;(2)在zp/C=0.37 处,出现首个up,z峰值,在颗粒端部靠近桨盘底面过程中,桨盘下方存在的负压区使颗粒减速上升,如图14(b)所示;(3)当zp/C=0.47 时,颗粒上端部接触桨盘底面,β达到最大值63.8°,up,z≈0,如图14(c)所示;(4)以颗粒上端部为支点,靠近槽底的下端部逐渐升高,并在压力梯度力的作用下加速上升,由此获得第二个up,z峰值,如图14(d)所示;(5)颗粒上、下端部基本平齐后(β=0),上部和下部基本无压力梯度,颗粒上升速度逐渐减小,如图14(e)所示。

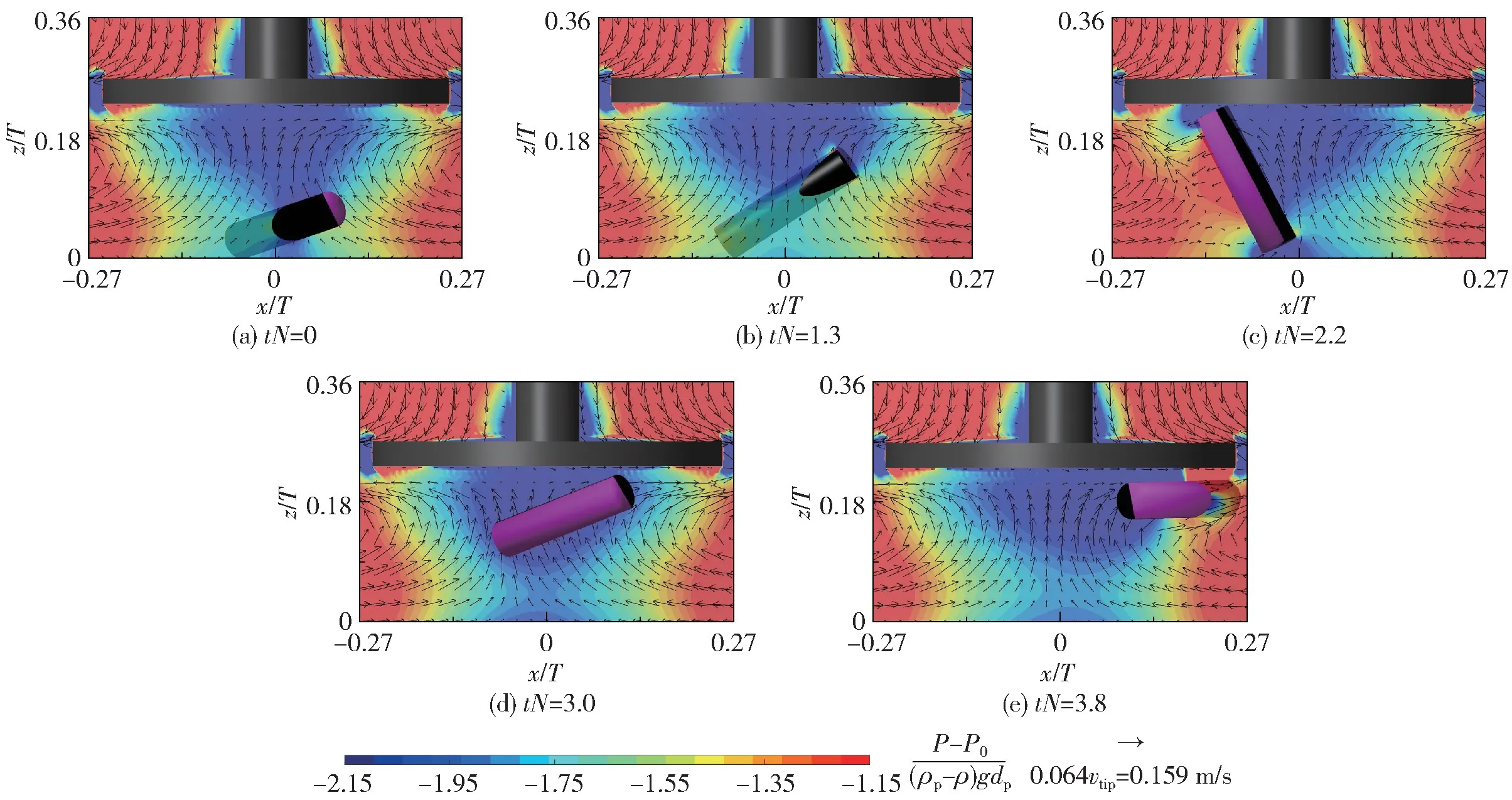
图14 dp =12Δ 且lp/dp =4 颗粒悬浮上升过程的瞬态流场和压力分布Fig.14 Instantaneous flow field and pressure in the lift-off process for the cylinder with dp =12Δ and lp/dp =4

颗粒在桨盘底部的运动轨迹如图13(f)所示。由于模拟时间步与实验时间存在差异,因此模拟和实验所得颗粒的运动轨迹有所不同,但具有类似的变化趋势。