基于统计分布信息的上市公司随机缺失数据的KNN 插补

李 夏,汪晓云,丁沈杰,张 玥

(安徽工程大学 数理与金融学院,安徽 芜湖 241000)

上市公司是我国企业中的优秀代表,是区域经济发展的稀缺资源,数量上只占全国企业数量的万分之一,但却是国家实体经济的“基本盘”。然而,上市公司财务数据缺失现象普遍存在,为上市公司财务状况的分析带来了挑战。

数据缺失不仅会降低数据的有效性,还会影响最终决策的准确性,因此对于缺失数据插补法的研究一直备受学者们的关注[1]。对于缺失数据的插补方法,可以分为两类:统计学插补法和机器学习插补法,而目前针对统计学插补法的研究要比机器学习插补法更加深入和广泛[2]。统计学插补法主要包括均值插补法、K 最近邻(K Nearest Neighbor,KNN)插补法、最大期望算法(Expectation Maximization algorithm,EM)插补法和多重插补法(Multiple Imputation,MI)等[3]。其中,KNN 插补法相对更稳定、准确性更高。KNN 插补法是一种基于相似测度的聚类算法[4],相似测度的选择会严重影响KNN 插补法的性能。由于相似测度有不同类型,这为该领域的研究留下了比较广阔的空间[5]。上市公司财务数据是由时间序列数据和截面数据结合而成的面板数据,而目前国内外的缺失数据插补法研究主要针对同一时期的截面数据或者同一个体的时间序列数据,对于面板数据的插补法研究尚处于起步阶段[6]。

面板数据兼具横截面和时间两个维度,因此包含更多的统计分布信息。传统KNN 插补法将数据空间视为欧氏空间,选择欧式距离来度量样本点间的毗邻关系,然而,高维数据空间一般是非欧的。因此本文将面板数据视为统计流形中的点,利用流形的测地距离来度量样本点间的邻近关系。考虑到统计流形上测地距离计算的复杂度,在KNN 插补法中,从多项式流形、参数假设检验、信息量这3个视角分别选择测地距离的近似测度:Cosine距离、Hotelling T2统计量和Jensen-Shannon散度,来度量样本间的相似性,并研究上市公司面板数据随机缺失状态下的插补效果。

1 KNN 插补法中3种度量

在高维数据空间中,欧氏距离不再适用,可以将高维空间近似为统计流形,用统计流形上的测地距离来度量数据点之间的邻近关系。由于测地距离计算复杂度高,很难获取其显式表达,因此本文用测地距离的近似测度:Cosine距离、Hotelling T2统计量和Jensen-Shannon散度来度量样本点间的相似性,距离越近,相似度越高。

1.1 Cosine距离

在统计流形中,距离的度量与欧式空间是不同的,一般都不是规则性的,也不像欧式空间需要对称,有很多距离都能够近似度量样本的相似性[7]。当有p和q两个分布时,将它们映射成统计流形上的多项式分布,用Cosine距离来度量数据间的距离。计算公式为:

1.2 Hotelling T 2 统计量

Hotelling T2统计量是一个无单位值,是t分布在多元条件下的推广,适用于度量高维数据之间的距离[8],计算公式为:

式中,n1和n2为样本容量;、S和分别为多元情况下的样本均值向量、样本方差-协方差矩阵和总体均值向量。

1.3 Jensen-Shannon散度

Jensen-Shannon散度来源于信息量,信息量是对事件的不确定性的度量,事件发生概率越小,信息量越大。当有p和q两个分布时,Jensen-Shannon散度是衡量q拟合p的过程中产生的信息损耗,信息损耗程度可度量两个分布之间的相似性,相同为0,相反为1。Jensen-Shan non散度是在Kullback-Leibler散度基础上引入的,和Kullback-Leibler散度相比,具有严格的对称性[9],取值范围是[0,1]。计算公式为:

2 实例与分析

上市公司财务数据属于面板数据,兼具横截面和时间两个维度。本文选择了107家上市公司2021年第三季度到2022年第一季度共3个季度的财务数据,其中多元金融板块有77家,商业银行板块有42家,保险板块有7家,共计321个样本。基于这些财务数据的统计分布信息,在KNN 插补法中,使用测地距离的近似测度:Cosine距离、Hotelling T2统计量和Jensen-Shannon散度,来度量样本间的相似性。

2.1 数据预处理

用Min-Max标准化对所有数值进行标准化处理[10],计算公式为:

式中,xi表示原始数据中的值;xmin和xmax分别表示该数据所在列中的最小值和最大值;x′i为标准化后的数值,取值范围为[0,1]。

2.2 实验结果

本文通过两个实验来测试基于统计信息下三种度量KNN 插补法的性能:一个是在同一缺失率下对它们的插补效果进行比较;另一个是在不同缺失率下,将它们与中位数插补法[11]、均值插补法[12]、缺失森林[13]、袋装法[14]、传统的KNN 插补法[15]这五种常用的插补方法进行比较。

(1)3种度量的KNN 插补法效果比较。本文选择在缺失率为12%的情况下,将样本数据随机挖空10次(不包括标签),生成10个随机缺失数据集,用10次实验结果的均方误差(Mean Square Error,MSE)和平均绝对误差(Mean Absolute Error,MAE)的平均值来衡量3种度量的KNN 插补法的性能稳定性,实验结果如表1所示。从表1可以看出,当缺失率为12%时,Cosine距离的MSE 和MAE 的平均值都是最大的并且误差也是最大的,它的MSE和MAE的平均值分别为5.164 7×10-3、1.549 4×10-2,对应的均方误差分别是7.545 9×10-4、1.620 4×10-3;其次是Jensen-Shannon散度,它的MSE平均值为3.804 5×10-3,误差为6.535 7×10-4;Hotelling T2统计量的MSE平均值是最小的,并且误差也是最小的,它的MSE 平均值为3.730 1×10-3,误差为5.927 9×10-4。由此可以看出,在缺失率较高的情况下,Hotelling T2统计量的KNN 插补法在这3种度量的KNN 插补法中插补的效果比较好,泛化性能比较稳定。

表1 缺失率为12%时3种相似测度的标准偏差

(2)与常用插补法的比较。考虑到当数据缺失率超过50%时,将有一定的概率使投影成为空集,因而本文将样本数据分别按照1%至15%,步长为1%的缺失率随机挖空(不包含标签),生成15个随机缺失数据集。将提出的三种度量的三种KNN 插补法分别与经典的、一流的五种插补法,即中位数插补法[11]、均值插补法[12]、缺失森林[13]、袋装法[14]、传统的KNN 插补法[15]进行比较,通过计算原始数据和插补后数据的MSE和MAE这两种统计指标来衡量这8种插补方法在不同缺失率情况下的插补效果,实验结果分别由图1、2所示。由图1、2可以看出,中位数插补法[11]、均值插补法[12]、缺失森林[13]、袋装法[14]和传统的KNN 插补法[15]这五种插补方法中,缺失森林方法效果最优,这是因为它可以直接用已观测到的完整部分数据集训练出的随机森林来预测缺失值,而不依赖于因变量的完整性[13];最差的是传统的KNN 插补法,而且其误差随着缺失率变大而陡增,说明其不适合填补缺失率大的缺失数据,这主要是因为在KNN 插补法的计算过程中,当缺失比例较大时,可能会出现大量数据连续缺失的情况,所以此时它很难对距离做出精确的测算,无法得出具体的插补结果。Cosine距离、Hotelling T2统计量和Jensen-Shannon散度这三种度量的三种KNN 插补法中,缺失率较低时,Cosine距离表现最优;缺失率较高时,Hotelling T2统计量表现最优。

图1 数据集插补结果MSE

由图1可见,当缺失率较低时,三种度量中,Cosine距离比较合适。当缺失率为1%~7%时,Cosine距离的MSE值与均值插补法比较接近,比Jensen-Shannon散度和Hotelling T2统计量的MSE 值要低,比缺失森林方法高出6.7‱;Jensen-Shannon散度的MSE值波动剧烈,是三种度量中表现最差的,比缺失森林方法高出5.5‰,比Cosine距离高出4.9‰。

随着缺失率的增大,当缺失率较高时,三种度量中,Hotelling T2统计量比较合适。当缺失率为8%~15%时,Hotelling T2统计量与袋装法以及均值插补法的MSE 值接近,比Cosine距离和Jensen-Shannon散度的MSE值要低,比缺失森林方法高出2.7‰;Jensen-Shannon散度的MSE 值波动仍然剧烈,是三种度量中表现最差的,比缺失森林方法和Hotelling T2统计量分别高出4.2‰和1.5‰。

由图2可以看出,当缺失率较低时,三种度量中,Cosine距离比较合适。当缺失率为1%~7%时,Cosine距离的MAE值与均值插补法比较接近,比Jensen-Shannon散度和Hotelling T2统计量的MAE值要低,比缺失森林方法高出2.3‰;Jensen-Shannon散度的MAE值波动剧烈,是三种度量中表现最差的,比缺失森林方法高出9.8‰,比Cosine距离高出7.5‰。

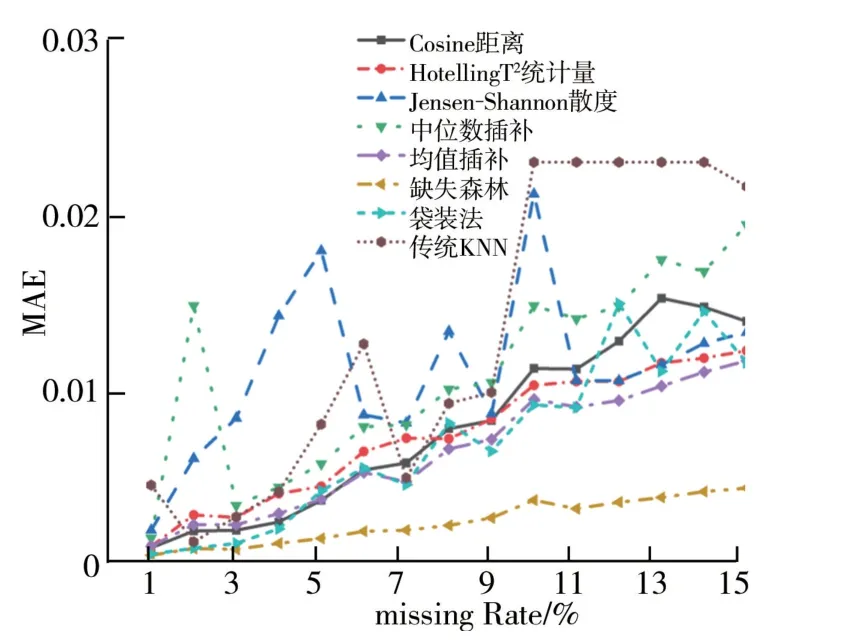
图2 数据集插补结果MAE

随着缺失率的增大,当缺失率较高时,三种度量中,Hotelling T2统计量比较合适。当缺失率为8%~15%时,Hotelling T2统计量与均值插补法的MAE 值接近,比Cosine距离和Jensen-Shannon 散度的MAE值要低,比缺失森林方法高出8.2‰;Jensen-Shannon散度的MAE 值波动仍然剧烈,是三种度量中表现最差的,比缺失森林方法高出1.1%,比Hotelling T2统计量高出2.9‰。

3 结论

缺失数据插补的理论及应用方面的研究成果近年来在统计、计量和医药等领域得到广泛的关注和应用。本文在国内外缺失数据插补的理论与方法的基础上,结合近几年来较新的缺失数据插补方法和面板数据的特点,提出了在KNN 插补法中,从多项式流形、参数假设检验、信息量这3个视角分别选择测地距离的近似测度:Cosine距离、Hotelling T2统计量和Jensen-Shannon散度,来度量样本间的相似性,并通过对107家上市公司的2021年第三季度到2022年第一季度共3个季度的财务数据进行随机缺失模拟,来测试基于统计信息下三种度量KNN 插补法的性能。主要有以下结论:Cosine距离、Hotelling T2统计量和Jensen-Shannon散度这三种度量的三种KNN 插补法中,当缺失率较低时,Cosine距离插补效果更优,略次于缺失森林方法;当缺失率较高时,Hotelling T2统计量插补效果最好并且具有良好的稳定性,弱次于缺失森林方法;Jensen-Shannon散度的误差波动性一直很大,但是在缺失率较高的情况下插补效果良好,这主要得益于在大样本数据的情况下,数据包含了更多的统计分布信息,参数假设检验和信息量这两个视角能够从统计分布角度更好地来考虑样本点间的邻近关系。