Chen 混沌系统数值仿真及其电路实现

蒋逢灵，刘贤群

（1.湖南铁路科技职业技术学院，湖南株洲，412006；2.湖南省高铁运行安全保障工程技术研究中心，湖南株洲，412006）

混沌系统是典型的非线性系统，具有随机性、遍历性以及初值敏感等特征，系统轨迹表现出及其的不确定性，非常适合于在安全通信[1]、密钥加密算法[2]以及图像处理[3]等方面中的应用，已经成为一门热门的学科研究。混沌系统经历了不同阶段的研究与发展，前期阶段主要关注混沌现象的揭示、混沌系统模型的搭建以及混沌理论的确定，而后期阶段的研究工作重点倾向于混沌模型的搭建与仿真、混沌理论的延伸以及混沌理论的应用等。随着计算机科学技术的发展，仿真技术已经成为科学研究中不可缺少的技术手段，利用仿真技术辅助科学研究，有助力缩短科学研究的周期，解决科学问题，降低科学研究的成本及风险[8]。Matlab/Simulink软件拥有强大的线性系统和非线性系统的分析功能，非常适合于混沌系统的研究，能够完成混沌系统的建模、仿真和分析等。并且混沌系统的动态仿真与电路实现，是认识混沌、应用混沌的基础。1983 年，美国华裔科学家蔡少棠教授首次提出了著名的蔡氏电路，证实了利用电子电路实现混沌现象的电路模型，开创了混沌电路产生混沌现象的先河[4]。随后研究者们利用电路元器件参数变化可调的便利，再通过运算放大器加减法、比例运算以及微分电路等实现了混沌电路，诞生了Chua’s 混沌电路[5]，Lorenz 混沌电路[6]、Chen 混沌电路[7]等混沌电路模型，这些研究成果为后来研究者研究混沌、分析混沌特性以及混沌应用提供了更多的参考价值。

根据Chen 混沌系统的微分方程，给出了系统方程的仿真建模流程，采用Matlab/Simulink 软件对Chen 混沌系统进行建模和仿真，通过观测器观测到了系统的混沌相空间吸引子和混沌时序图。最后利用电路原理，在Multisim 中搭建Chen 混沌系统模型进行电路实验仿真，结果表明系统存在混沌现象，实验结果进一步验证了混沌电路同样是混沌的，与前面动态仿真结果完全吻合。文中利用动态仿真和电路实现揭示了混沌现象，把抽象的混沌理论，复杂的混沌动态状态该仿真通过仿真软件简明、直观的展示，有利于为从事混沌理论及应用研究提供很好的参考价值，为混沌系统及实验教学提供了新途径。

1 Chen 混沌系统的Matlab 仿真

Chen 混沌系统，与Loren 系统、Chua’s 系统和Rssler 系统都是最具有代表性的混沌系统[9]，其中Chen系统的状态方程为：

其中x，y，z为系统变量，常数a，b，c系统（1）的参数，在电路实现中可以通过改变电阻的取值改变常数的值。

Matlab 数值仿真就是根据系统（1）的数学表达式通过软件程序的编写，将数学公式抽象化的理论知识通过计算机的处理图形化或者数值化，解决复杂问题的分析，但其缺点是受制于仿真速度较慢，以及无法演化系统的动态仿真过程，只能得到最终的输出结果。其具体的仿真思路如图1 所示，首先在Matlab 中编写M 文件，将系统状态方程的数学公式进行转换，通过编程语言设置参数和初始值等参数，输出系统图形，最后根据输出相图分析系统是否为混沌系统。

图1 Matlab 数值仿真流程

以整数阶Chen 混沌系统为例，在数值仿真参数设定中取系统（1）的初始值x(0)=10，y(0)=10，z(0)=10，a=35，b=3，c=28，在Matlab 中运行程序，输出Chen系统的三维相空间吸引子如图2 所示。

图2 Chen 系统三维相空间吸引子

2 Chen 混沌系统的Simulink 动态仿真

Simulink 是Matlab 软件中重要的组成部分之一，具有功能强大，使用简单方便的优点，是一种有效的可视化仿真工具，非常适合于动态系统的数学建模、仿真与分析，不需要编写大量复杂的程序，只需要根据系统表达式建立模块化模型，并且仿真效果直观，非常适合于复杂非线性系统的仿真分析。

Simulink 有数十种以上的功能集合，文中对系统（1）进行动态数值仿真主要用到Simulink 功能集中“Simulink Library Browser”，里面涵盖了系统建模、函数调用、运放、数学运算以及状态监控等功能。具体流程如图3 所示。

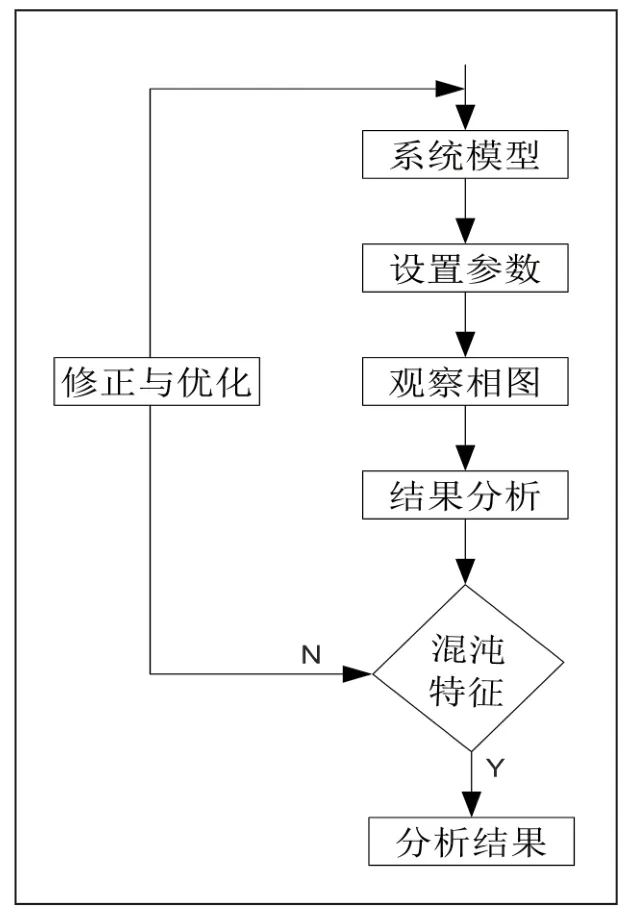
图3 Simulink 数值仿真流程

在Simulink中建立Chen 系统的仿真模型如图4所示。

图4 Chen 系统Simulink 数值仿真模型

图3 中Gain 表示数乘放大，对应系统（1）中的a，b，c，可以通过修改Gain 的值进行改变系统参数的值。Product 表示变量的乘法“X”运算，“1/S”表示积分。仿真设置参数a=35，b=3，c=28，运行仿真时间50，通过观测器观察系统的二维空间相图如图5所示，x，y 相的时序图如图6 所示，从图5 和图6 发现Chen 系统是混沌的。

图5 Chen 系统x-y 相图

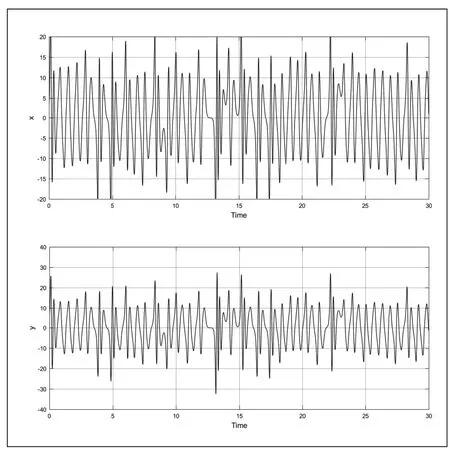
图6 x，y 的时序图

3 Chen 混沌系统的电路仿真

混沌系统的动态仿真研究是基于计算机仿真手段分析混沌特征的重要手段，而混沌系统电路实验是混沌系统在实际工程中应用需要解决的问题。混沌系统因为初始值敏感的特性，一点点细微的差别，导致结果天壤之别，对实际电路实验提出了极其苛刻的要求，需要高精度、高可靠的实验元器件。随着计算机技术的法阵，构造出很多辅助演示研究的仿真平台，其中Multisim 电路仿真平台就能很好地解决混沌电路的仿真问题，能够获得效果显著的系统仿真结果。

基于电路原理知识，根据Chen 混沌系统的数学表达式，利用运算放大器虚短和虚断的原理设计系统的电路模型，其中运算放大器（LF347BD）主要实现数学公式的加减计算、变量的反相器设计以及微分方程等运算，模拟乘法器AD633 实现Chen 混沌系统的非线性变量的运算如图7 所示。

图7 系统电路原图

运算放大器电压等级如图7 所示，取±18V。为了有效的对系统电路进行仿真实验，这里将输出变量的信号缩小到原理的1/10，设变量 u=10x1，v=10x2，w=10x3，其输出结果不会影响系统的性能，令u=x，v=y，w=z，则系统（1）变换为：

根据电路理论以及电器元器件的运算，设计出仿真电路为：

由式(2)和式(3)可得：

由式(4)和式(5)，取系统参数如表1 所示。

表1 Chen混沌系统电路参数

由Chen 混沌系统参数计算可得到a=35，b=3，c=28，在Multisim电路仿真中对电路进行仿真，通过示波器观察到系统（2）的二维及时序相图如图8～图11 所示，从图8～图11中可以看出，系统（2）是混沌的，与系统（1）仿真结果完全项吻合，验证了电路实验的可行性与准确性。

图8 x-y 二维空间相

图9 x 时序图

图10 y 时序图

4 结束语

根据Chen 系统动态方程，采用Matlab/Simulink 仿真软件实现了Chen 混沌系统的建模和动态仿真，给出了仿真建模的流程，并对模型进行仿真分析，系统确实存在混沌相图吸引子和时序图。最后在Mulitisim 中搭建Chen 混沌系统电路模型，设置合适的电路元器件参数，通过示波器观察系统是混沌的，并且电路实验结果与数值动态仿真结果完全相吻合。文中采用多种仿真软件对Chen 混沌系统进行动态仿真与电路实现，把混沌系统抽象化的问题具体直观化，在一定程度上弥补了科学研究者物理实现的短板，同时也为后续从事混沌理论及应用研究提供参考价值，为混沌系统和混沌实验研究提供新途径。