关于汽车板DP用钢流动曲线模型的研究

张东凯,李晓广,李弋坤,余亚克,穆康奇

(1.河钢集团邯钢公司,河北 邯郸 056000)

研究表明,汽车重量每减轻10%,汽车油耗和排放可以降低6%～8%[1]。当下国家积极推动双碳目标,汽车节能减排大势所趋,全球汽车产业正处于升级换代阶段,一方面新能源汽车迎合而上迅猛发展,另一方面,传统油车加快汽车零件材质强度升级。为了使汽车节能减排,轻量化是一种有效的途径。轻量化设计逐渐采用较薄的DP双向钢来替换厚重的普板。高强汽车板DP用钢常采用冷冲压或辊压成形工艺。成形前会进行成形仿真,分析成形性、减薄率及开裂风险等。流动曲线作为成形仿真材料卡片的一项重要输入参数,它决定着成形仿真的精度及可靠性。国内外很多学者对流动曲线模型进行了研究[2-8]。董伊康[9]采用6种流动曲线模型研究了HC420/780DP钢在大应变范围内的差异。Sebastian Dziallach[10]采用DIC和液压胀形设备对DP600大应变范围内的流动曲线模型拟合效果进行了研究。林启权[11]对比分析了BP神经网络模型和VOCE模型对DP980钢板的预测精度。熊鹏鹏[12]构建了深度神经网络硬化模型来预测DP780在不同的预应变下下的流动应力。李宏烨[13]采用8种流动曲线模型对中厚板材料的拉伸曲线进行了拟合,通过均方差和相关系数分析了拟合精度。刘国承[14]采用Swift模型、Voce模型、Swift-Voce模型研究了各向异性材料在塑性成形全段的变化过程。刁有凯[15]采用不同的模型对QP1180进行曲线拟合,用相关系数分析了拟合效果。

当下对汽车板DP用钢流动曲线模型的研究较少,且钢种数量单一,钢的强度在600 MPa左右,更高强度的DP钢研究更少。为了较系统地研究汽车板DP用钢流动曲线模型,选取了HC340/590DP、HC450/780DP、HC650/980DP、HC820/1180DP汽车板DP用钢。对于流动曲线模型,新构建了LOGSE流动曲线模型,同时引入成形仿真中常用的Combined Swift-Hockett-Sherby模型(简称Combined S-H模型)、Hockett-Sherby模型、 Ghosh模型、Swift模型,用这些模型对汽车板DP用钢的单向拉伸曲线进行拟合,分析了均匀塑性变形阶段的拟合效果。以DP600[10]单向拉伸曲线为拟合目标,结合该材质的液压胀形等效应力等效应变曲线,分析不同模型在大塑性变形阶段的变化趋势。

1 新流动曲线模型

构建了一种新的非饱和LOGSE模型,即

σ=σs+a·ln(1+b·εp)

式中σ为真应力,ε为真塑性应变,σs为屈服强度,a、b、p为大于零的拟合参数。

成形仿真常用流动曲线模型有Combined S-H模型、Hockett-Sherby模型、Ghosh模型、Swift模型,表达式如下:

Combined S-H模型在Swift模型和Hockett-Sherby模型之间引入权重系数α,通过调整权重系数来优化拟合曲线:

σ=(1-α)[C(ε+ε0)p1]+α[σsat-(σsat-σs)exp(-aεp2)]

式中:C、ε0、p1、σsat、a、p2为大于零的拟合参数。

Hockett-Sherby模型为饱和模型,随着塑性应变增大,真应力趋于定值,初始值为屈服强度:

σ=σsat-(σsat-σs)exp(-aεp)

式中:σsat、a、p为大于零的拟合参数。

Ghosh模型为非饱和模型,无初值:

σ=C(ε+ε0)p-D

式中:C、D、ε0、p为大于零的拟合参数。

Swift模型为非饱和模型,无初值:

σ=C(ε+ε0)p

式中:C、p为大于零的拟合参数。

2 均匀塑性变形阶段分析

对HC340/590DP(简称DP590)、HC450/780DP(简称DP780)、HC650/980DP(简称DP980)、HC820/1180DP(简称DP1180)进行单向拉伸试验,得到工程应力应变曲线和拉伸力学性能。采用LOGSE、Combined S-H、Hockett-Sherby、 Ghosh、Swift流动曲线模型对均匀塑性变形阶段的真应力-塑性应变曲线拟合。

2.1 真应力-塑性应变曲线

依据《GB/T228.1-2010 金属材料拉伸试验第1部分:室温试验方法》对DP590、DP780、DP980、DP1180进行单向拉伸试验,拉伸曲线见图1,力学性能见表1。由于颈缩现象导致抗拉强度后的曲线数据无效,所以先去除单向拉伸曲线中的颈缩数据,再提取有效数据的塑性变形,获取工程应力-塑性应变曲线,根据式(1)将工程数据转换成真应力塑性应变曲线,见图2。

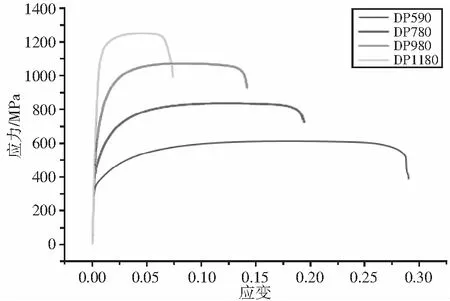
图1 不同牌号材料的拉伸曲线

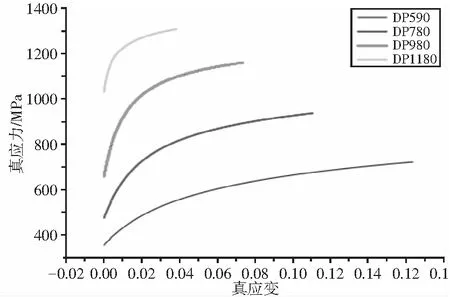
图2 真应力塑性应变曲线

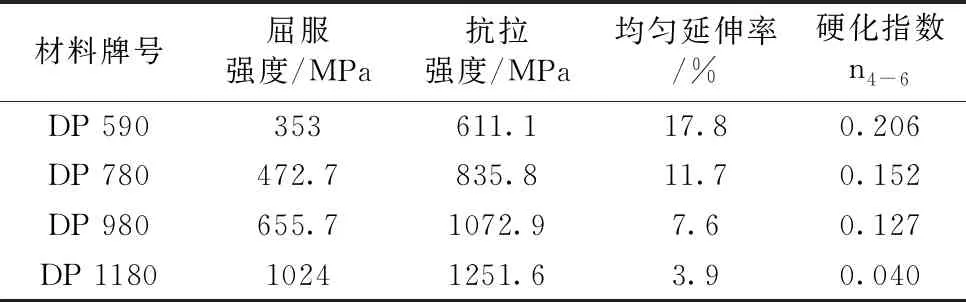
表1 拉伸力学性能

ε=ln(1+εE)

σ=σE(1+εE)

(1)

式中,σE为工程应力,εE为工程应变。

2.2 曲线拟合

根据真应力塑性应变曲线,采用上面的模型拟合,结果见图3。

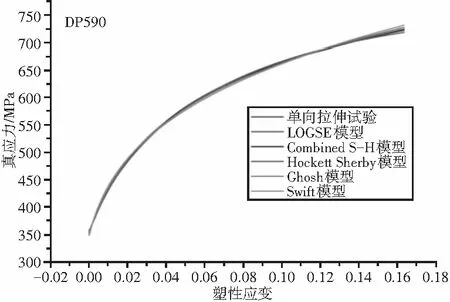
(a)

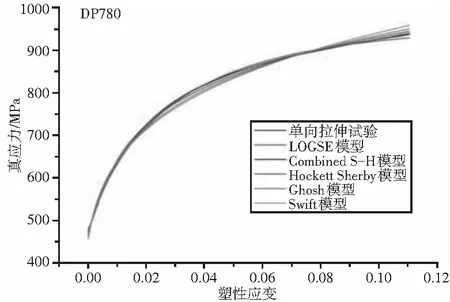
(b)

(c)

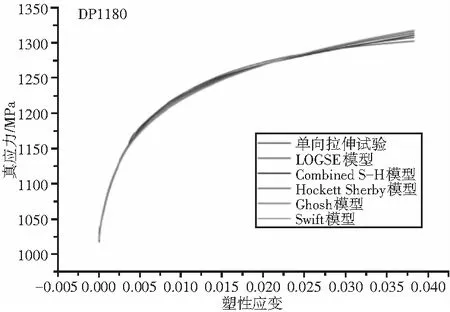
(d)图3 拟合结果

2.3 拟合分析

H.J.KLEEMOLA[6]等学者从均匀延伸率角度对流动曲线模型拟合精度进行了研究。李宏烨[13]等学者基于均方根和相关参数对8种模型拟合精度进行了研究。为了全面评价拟合精度,此次研究考虑了曲线拟合的起点、终点、误差绝对值及误差分布,即从均方根、相关参数、均匀延伸率及屈服强度四个方面分析拟合精度,得出了一些研究结果,为汽车板DP用钢在均匀塑性变形阶段的冲压成形仿真提供参考。

该书一上市就引起了大规模的哄抢，贾宝玉签名售书那天人山人海，道路交通阻塞，三百余名警察维持秩序尚不能平息混乱。几天的日报晚报更是刊登巨幅照片，轰炸报道。几乎被人遗忘的林黛玉再度成为小资敢爱敢恨的典范，她的旧诗词也一并被再版后摆上书店橱窗，被小资们竞相模仿。这天，贾宝玉被熙攘的找他签名的人潮挤得头昏脑胀，突然听到一曲《传奇》，时近时远，如梦似幻——原来林妹妹常唱给他听的，不禁心下黯然。与此同时，薛蟠投巨资包装的薛村，找人写歌，谱曲，用韩语演唱的《你在他乡还好吗》，不想被另一歌手抢先四川话翻唱，一时红遍大江南北。

2.3.1 均方根分析

均方根(RMSE)是拟合数据yi与试验值yi′偏差的平方与数据个数n比值的平方根,可以衡量一组数的离散程度,其计算公式如下。

(2)

根据式(2)计算拟合曲线与试验曲线之间的均方根,结果见图4。

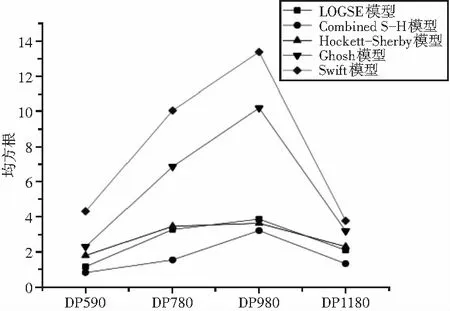
图4 不同模型拟合的RMSE

在图4中, Combined S-H模型的均方根最小,在1.7左右。LOGSE模型与Hockett-Sherby模型的均方根在2.7左右,相差不大。Ghosh模型的均方根在5.6左右,Swift模型的均方根在7.9左右。由于均方根越小,拟合曲线与试验曲线的拟合精度越高,所以对于以上四种DP钢,在均匀塑性变形阶段,模型拟合精度最高的为Combined S-H模型,其次为LOGSE模型和Hockett-Sherby模型,较次为Ghosh模型,最次为Swift模型。

2.3.2 相关系数分析

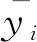
(3)

由式(3)得到的不同模型拟合的相关系数见图5。图中 Combined S-H模型的相关系数平均为0.9998,LOGSE模型的相关系数为0.9996,Hockett-Sherby模型为0.9995,Ghosh模型为0.998,Swift模型为0.996,模型的相关系数均大于0.98,说明模型都可以很好地解释均匀塑性变形阶段的应力应变曲线。

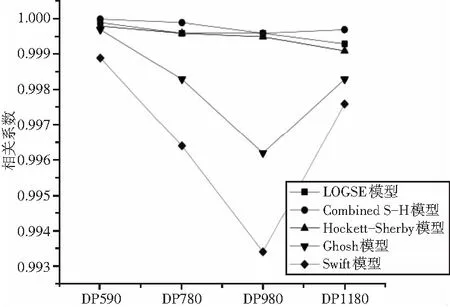
图5 不同模型拟合的相关系数

2.3.3 均匀应变分析

(4)

根据公式(4),由上述模型计算的均匀应变见表2,其与试验值的误差见图6。

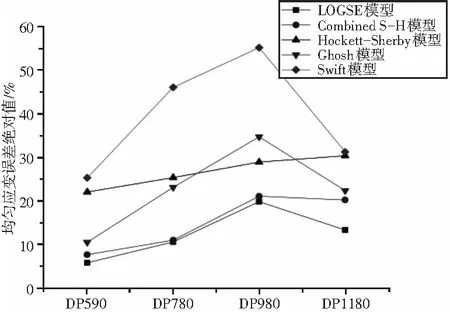
图6 不同模型拟合的均匀应变误差

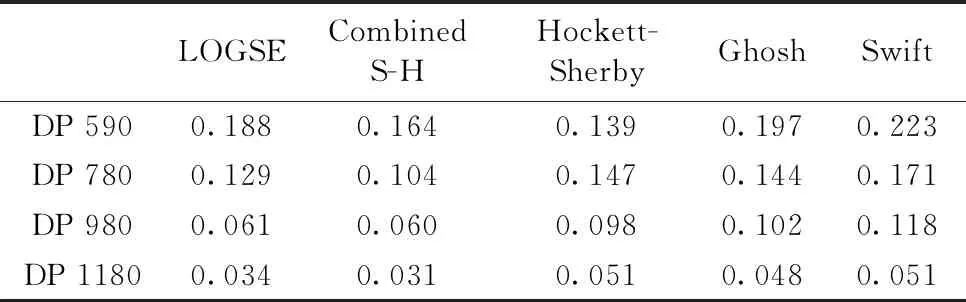
表2 流动曲线模型预测的均匀应变

从图6可以看出,LOGSE模型计算的均匀应变误差绝对值在5.8%到19.8%之间。Combined S-H模型计算的误差绝对值在7.6%到21.1%之间,Ghosh模型计算的误差绝对值在10.5%到34.7%之间,Hockett-Sherby模型计算的误差绝对值在22.1%到30.4%之间,Swift模型计算的误差绝对值在25.3%到55.2%之间。

LOGSE模型计算的均匀应变与试验结果最为接近,其次为Combined S-H模型,再次为Ghosh模型和Hockett-Sherby模型,Swift模型计算的均匀应变与试验结果相差最大,对DP980汽车板用钢的误差达到55%。

2.3.4 屈服强度分析

屈服强度是弹性变形和塑性变形的分界点,标志着材料开始出现塑性变形,它是成形仿真的一个关键参数。将ε=0代入流动曲线模型,便可计算得到屈服强度。

不同模型计算的屈服强度见表3。计算值与试验值的百分比偏差见图7,负号表示计算值比试验值小。

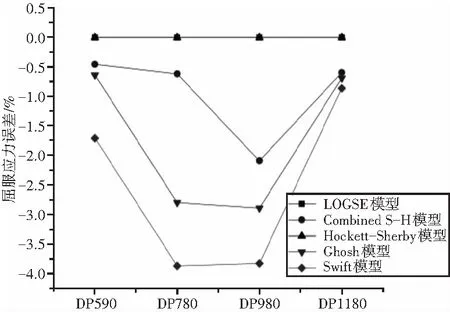
图7 不同模型拟合的屈服强度偏差

表3 流动曲线模型预测的屈服强度 单位:MPa

从图7可以看出,LOGSE模型和Hockett-Sherby模型计算的屈服强度误差为零,这由函数模型本身决定。Combined S-H模型、Ghosh模型、Swift模型的预测值相对于试验结果都偏小, 其中Combined S-H模型预测值误差在-2.1%到-0.5%之间,Ghosh模型预测值误差在-2.9%到-0.63%之间,Swift模型在-3.8%到-0.9%之间,模型误差值都很小。

3 大塑性变形阶段的流动曲线分析

在均匀塑性变形阶段(小于均匀延伸率的塑性变形),不同模型的相关系数都大于0.98,均方根在0～8之间,拟合精度都很高。但是,在大塑性变形阶段(大于均匀延伸率的塑性变形),流动曲线开始出现较大差异。

为了分析这些差异,以DP600[10]为研究对象,利用由液压胀形试验所测得的等效应力等效塑性应变曲线来延长由单向拉伸试验测得的均匀塑性变形曲线(曲线外推),见图8。

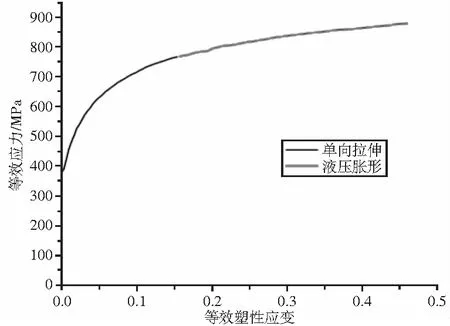
图8 曲线外推

将不同的流动曲线模型拟合图8中的单向拉伸均匀应变曲线,模型在大塑性变形阶段的曲线与液压胀形外推曲线的对比见图9。

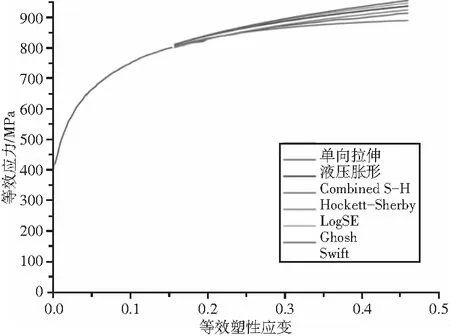
(a)

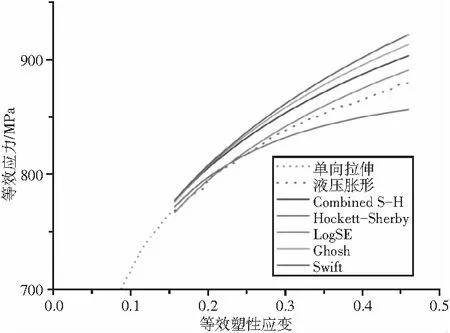
(b)图9 不同流动曲线模型比较

从图中可以看出,随着塑性应变加大,各个模型的应力变化差异越大。曲线从上到下依次为Swift模型、Ghosh模型、Combined S-H模型、LOGSE模型、液压胀形试验曲线、Hockett-Sherby模型。

大塑性应变阶段,Swift模型、Ghsoh模型、Combined S-H模型及LOGSE模型预测的结果都偏大,而Hockett-Sherby模型偏小。

不同模型计算得出的屈服强度、抗拉强度及均匀延伸率见表4,LOGSE模型和Combined S-H模型都较准确的计算出服强度、抗拉强度及均匀延伸率。

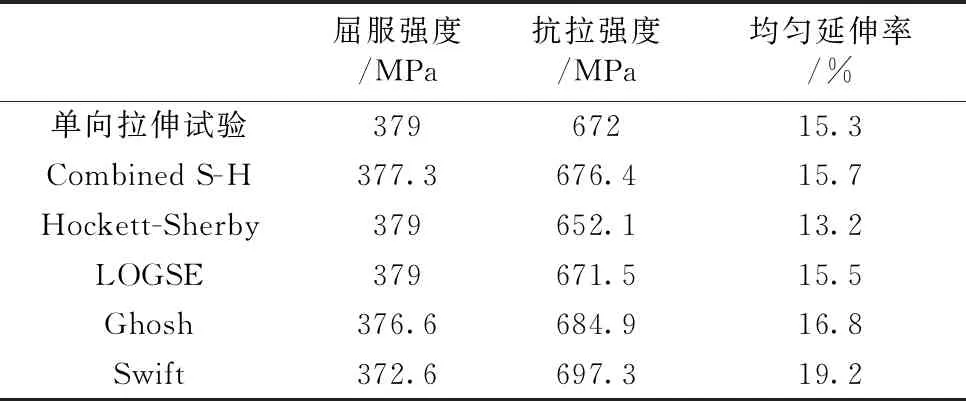
表4 不同模型计算的力学性能

模型与液压胀形试验曲线之间的差距可由均方根来反应,不同模型在大塑性变形阶段的变化与液压胀形试验所测的等效应力等效塑性应变曲线的偏差见表5。从表中可以看出,均方根最小的是LOGSE模型,其值为5.4,与液压胀形试验曲线最为接近。Hockett-Sherby模型对应的均方根为9.8, Combined S-H模型对应的均方根为15.9, Ghosh模型对应的均方根为20.6,Swift模型对应的均方根为24.6。

表5 不同模型的外推误差

结合图9和表5可以看出,汽车板DP600用钢在大塑性应变阶段,Swift模型、Ghsoh模型预测结果较差,Combined S-H模型次之, LOGSE模型和Hockett-Sherby模型预测结果较准确。

(a)

(b)

(c)

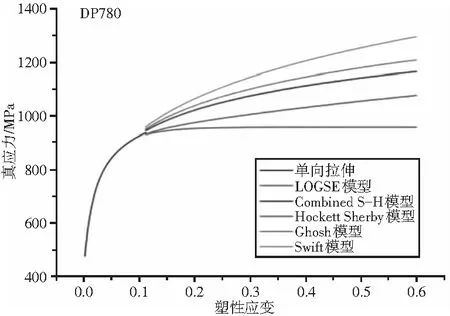
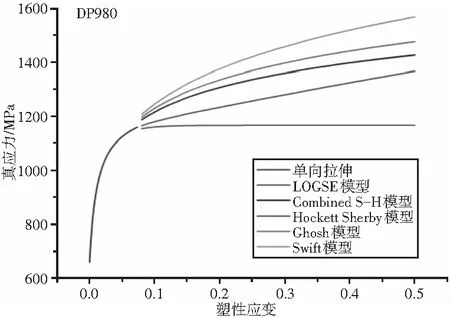
(d)图10 大应变阶段不同流动曲线模型比较

将不同模型对汽车板DP590、DP780、DP980、DP1180用钢单向拉伸曲线进行外推,结果见图10。从中可以看出,模型在塑性变形阶段出现较大差异,应力由大到小为Swift模型、Ghosh模型、Combined S-H模型、LogSE模型、Hockett-Sherby模型。结合图9和图10 为汽车板DP用钢成形仿真提供参考。

4 结 论

(1)构建了一种新的对数形式的流动曲线模型,即LOGSE模型,引入了4个参数。该模型在均匀塑性变形阶段和大塑性变形阶段都表现出很好匹配精度。

(2)采用LOGSE模型、Combined S-H模型、Hokcett-Sherby模型、Ghosh模型、Swift模型对DP590、DP780、DP980、DP1180汽车板用钢的拉伸曲线进行了拟合,可以发现:

在均匀塑性变形阶段,模型拟合精度都较高,相关系数都在0.99以上。均方根在1.1到13.4之间,拟合精度较高的为Combined S-H模型、LOGSE模型、Hokcett-Sherby模型,较差的为Ghosh模型,最差的为Swift模型。

在大塑性变形阶段,流动曲线模型差异逐渐拉大,但有一定的规律性。应力由大到小为Swift模型、Ghosh模型、Combined S-H模型、LOGSE模型、Hokcett-Sherby模型。

对于DP600,LOGSE模型曲线与液压胀形曲线最为接近,其次为Hockett-Sherby模型、再次为Combined S-H模型,较差的为Ghosh模型,最差的为Swift模型。