连续型机器人运动学的平面圆弧法建模与实验研究
2023-12-07高源臧红彬袁卫锋周军尹强李成佳蔡勇刘樾
高源,臧红彬,袁卫锋,周军,尹强,李成佳,蔡勇,刘樾
(西南科技大学 制造过程测试技术省部共建教育部重点实验室,四川绵阳 621010)
作为仿生机器人的一种,连续型机器人由多段 连续体关节组成[1],具有自由度多、灵活性好的特点,面对复杂的作业环境与狭小的工作空间具有其独特的优势。连续型机器人机械臂形状可以灵活改变,不仅可以在机械臂末端搭载不同执行器完成拾取和夹持等不同任务,还可以通过自身机械臂本体的弯曲,对目标进行缠绕并抓取[2]。因此,连续体机器人可广泛应用于受限空间作业[3],例如复杂的工业环境、自然灾害的侦测与搜救作业、核电站管道探测与维护以及人体微创手术等领域。
连续型机器人的运动学逆解一直是该类机器人运动学研究的难点问题之一,对机器人的动态特性分析、路径和运动规划、运动控制等[4]研究工作具有重要意义。逆运动学求解方法主要包括:几何法、数值解法和智能算法。数值解法通常需要计算机器人雅克比矩阵,并给定初始值进行迭代计算。这种方法存在计算量庞大,雅克比矩阵奇异等问题。智能算法主要问题在于计算速度慢、实时性差,且无法保障算法的收敛性。从求解复杂度来看,几何法具有精度高、计算快的特点,使其成为一种更优越的逆运动学算法[5]。
目前,国内外学者对连续型机器人运动学进行了大量研究,并取得了相应的研究结果。胡海燕等[6]设计了一种应用于结肠镜检查的连续型机器人,利用几何分析法建立了机器人的运动学模型。文献[7-9]设计了双枢轴结构的连续型机器人,解决轴向扭转问题并采用D-H 法建立了运动学模型。文献[10-11]针对民航飞机油箱复杂内部结构,仿照蛇脊椎结构设计连续型机器人,利用几何分析法建立运动学模型,并进行实物样机实验。目前大多数研究主要针对连续型机器人的机械系统设计和正向运动学分析,未对多级关节逆运动学问题进行研究。Qin 等[12]采用分层驱动原理,使单个连续关节中具有多个刚体关节,实现角同步运动,降低逆运动学求解复杂度。Godage 等[13-14]提出了采用模态形状函数(MSF)的连续体机器人运动学模型,并引入运动解耦特性求解逆运动学问题,该方法精确且避免了奇异性,但计算较为复杂。李旻翰等[15]提出了一种由三自由度局部并联机构组成的连续型机器人运动学建模方法,并借助雅克比矩阵在微分运动的水平上运用线性代数,求解其逆运动学数值解,该机构具有冗余自由度,仍然存在雅克比矩阵奇异、无数解等问题。方跃法等[16]设计了一种连续体并联抓取机器人,运用等效D-H 法建立起运动学模型,并求解其正、逆运动学解,该机器人仅有3 个自由度,其运动学逆解问题相对简单,具有封闭解,不具备通用性。赵志刚等[17]提出了一种气动连续体机器人关节结构,并采用修正的D-H 法建立了运动学模型,求解了正逆运动学解,但仅针对单级关节进行了运动学逆解,无法适用于多级关节的连续型机器人。因此,简单、高效求解连续型机器人多级关节复杂逆运动学问题的方法的研究仍需不断深入。
在此背景下,本文提出利用平面圆弧法建立连续型机器人的运动学模型。分别采用单圆弧和双圆弧拟合连续体机器人的弯曲形状,对其驱动空间、关节空间和操作空间的映射关系进行分析,并描述其工作空间。针对操作空间至关节空间的逆运动学问题中末端位置求解问题,该运动学模型利用圆弧法的几何约束,建立关节空间变量之间的数学关系,减少求解变量数量,降低求解难度。利用MATLAB进行运动学仿真与逆运动学求解,并制造原理样机进行实验,验证了运动学模型的正确性与逆运动学求解的有效性。
1 连续型机器人系统
图1 为本文所研制的连续型机器人系统,主要由驱动机构和连续型柔性臂组成,用于高约束和非结构化的复杂环境中。连续型柔性臂本体长度为L=609 mm,由3 段空间连续型关节组构成,每段关节组长度La=203 mm, 末端执行器长度Lb=110 mm。每段连续型关节组由7 个小关节体串联构成,其极限弯曲角度为1 20◦;构成3 段关节组的关节体直径分别为95 mm、80 mm、65 mm。
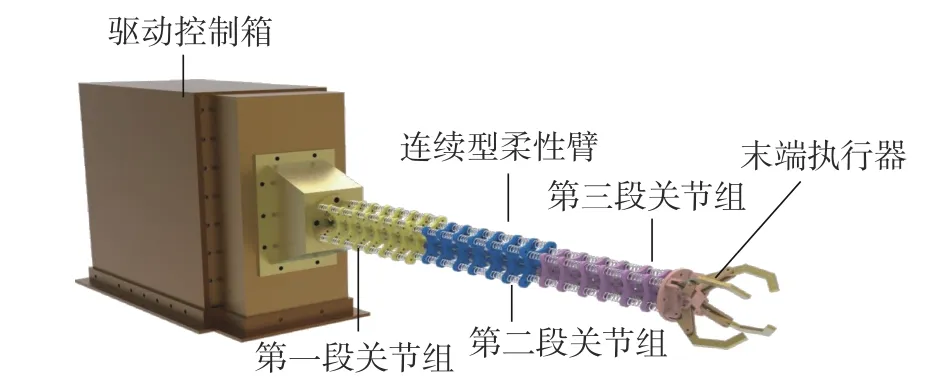
图1 连续型机器人系统Fig.1 Continuous robot system
关节体是组成柔性臂的基本单元,关节体之间采用具有两自由度的十字铰链连接。关节体的外边缘均布着12 个直径为3.5 mm 的过孔,每4 个间隔为 90◦的绳孔为一组,用于通过直径为2.5 mm 的驱动绳,每两个对应的绳孔之间嵌入有弹簧(压簧),驱动绳不仅要穿过关节体上的过孔,还需穿越关节体之间的弹簧内部。在关节体弯曲过程中,弹簧始终处于被压状态,以提高柔性臂的柔顺性。所使用弹簧的长度为30 mm,线径为1.5 mm,直径为10 mm。12 根驱动绳分为3 组,第一组驱动绳通过基座和第一段关节组后固定在第7 个关节上;第二组驱动绳通过基座和第一段、第二段关节组后固定在第14 个关节上;第三组驱动绳则通过所有关节组后固定在柔性臂末端关节体上。每组驱动线分别对连续型柔性臂每段关节组进行冗余驱动,实现每段关节组2 自由度弯曲运动。
2 连续型柔性臂运动学构建
本文采用一种平面圆弧方法建立运动学模型,建立连续型柔性臂的操作空间、关节空间和驱动空间之间的数学映射关系。该方法将柔性臂中心轴线弯曲形状视为二维平面中一条连续光滑曲线,将运动学问题从三维空间降维到二维平面,使得逆运动学求解具有高效性和有效性。对于该运动学方法,作出如下假设:
1)连续型柔性臂在弯曲时符合常曲率模型,为曲率相等的连续光滑曲线。
2)两关节间距足够近,驱动线在柔性臂弯曲过程中为等曲率的圆弧曲线。
3)弹簧具有很好的一致性,从而忽略弹簧自身误差造成的影响。
2.1 运动学模型构建基础
连续型柔性臂整体长度为L,其随体坐标系及各个变量定义如图2 所示。图2 中,设柔性臂初始位置竖直向上,以连续型柔性臂基座端面的圆心为原点,建立全局坐标系O1, 沿柔性臂轴向为x1,由原点指向基座端面上两个间隔为 90◦的绳孔的中点为y1,建立右手坐标系,则柔性臂初始末端坐标点为A=(L,0,0)。柔性臂在驱动绳的牵引下进行弯曲运动,柔性臂末端在全局坐标系中的位置点为EO1(xe,ye,ze), 根据点A、O1、E这3 点即可确定柔性臂形状曲线所在平面B。位置点E在基座标系中y1-O1-z1面的投影点为E0,则以全局坐标系的O1为原点,沿柔性臂轴向为x2方 向,OE0为y2方向,建立局部坐标系O2。 平面B则为局部坐标系O2中的平面,柔性臂中心轴线的弯曲形状即可视为平面B中的一条连续光滑曲线S。

图2 柔性臂三维空间弯曲运动模型Fig.2 Three-dimensional bending motion model of a flexible arm
本文后续的研究将针对平面B中的柔性臂形状曲线进行讨论。将基坐标系O1中的柔性臂末端位置点E(xe,ye,ze)通 过坐标转换后在坐标系O2中进行表达。如图2 所示,坐标系O2为 全局坐标系O1绕x1轴旋转角度φ 后所得到,坐标系O1到O2的转换矩阵为

2.2 坐标转换
连续型柔性臂本体末端位置点E(xe,ye,ze),在坐标系O1中 的位置描述为EO1, 在坐标系O2中的坐标描述为EO2。EO1与EO2的转换关系为
3 单圆弧曲线的运动学模型
本文在二维平面B 内对柔性臂进行运动学分析,首先以单圆弧曲线拟合柔性臂弯曲形状。如图3所示,柔性臂的几何形状由直线段H和圆弧段L0共同组成,关节空间的变量为h、 θ和R,其中h为直线段H的长度, θ为圆弧段L0的圆心角,R为圆弧段L0的半径。
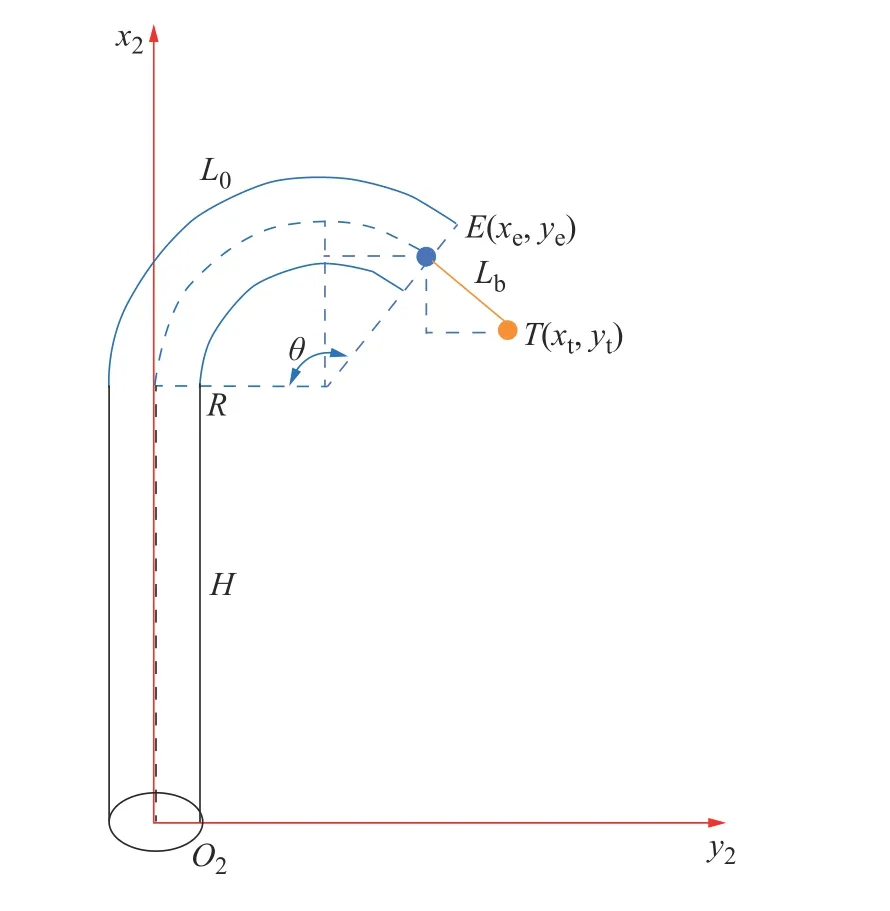
图3 柔性臂单圆弧弯曲运动几何模型Fig.3 Geometric model of single circular arc bending motion of a flexible arm
3.1 操作空间与关节空间的运动学分析
操作空间与关节空间的运动学分析即为柔性臂末端点EO2(xe,ye,ze)与 关节空间变量h、 θ和R之间的映射关系,可通过图3 的几何模型可以得到:

式(7)中的xe、ye、L已知,左边为关于 θ的一维函数,因此对 θ的求解是一维目标函数搜索问题。采用二分法进行搜索,以 θ的取值区间( 0,2π]作为搜索区间,搜索该区间内满足式(7)的 θ最佳解。当搜索得到 θ的最佳解后,将其代入式(8)和式(9)可求得关节空间变量R和h。
在实际工作中,柔性臂通过末端执行器完成抓取操作。如图3 所示,以目标点TO2(xt,yt,zt)作为末端执行器抓取范围中心的位置点,从柔性臂末端到执行器抓取中心点的距离为Lb= 110 mm,在图中以长度为110 mm 的直线段来表示。根据图3 中的几何关系可得:
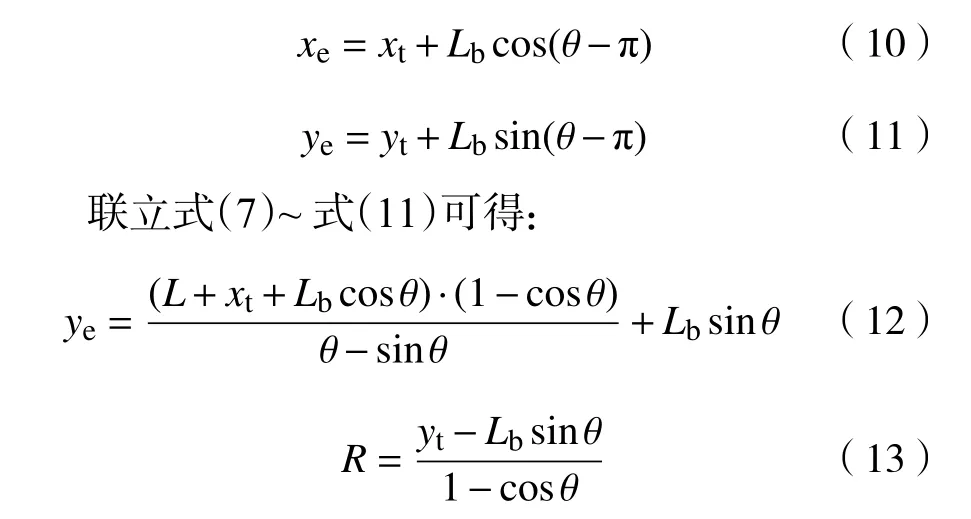
式(12)反应了独立关节变量 θ和目标点TO2(xe,ye,ze)位置的逆运动学映射关系,同样是关于θ的一维目标函数搜索问题,依然采用二分法进行搜索求解。考虑末端执行器后二分法计算过程更为复杂,但依然属于一维函数的计算,对该逆运动学算法的时间复杂度与空间复杂度影响较小。
柔性臂每段关节组存在极限弯曲角度,在得到满足约束条件关节空间变量h、 θ和R后,有必要验证θ 是否超过了每段关节组的极限弯曲角度。当θ 的解位于 [2π/3,4π/3],通过弧长公式可计算得到圆弧段长度L′, 若L′<203 mm,则超过单段关节组极限弯曲角度;当 θ 的 解位于 [4π/3,2π],计算得圆弧段长度L′, 若L′<406 mm,则超过了两段关节组极限弯曲角度,此时的h、 θ和R不能作为有效的解,应继续采用二分法求解。
3.2 关节空间与驱动空间的运动学分析
连续型柔性臂的弯曲运动是通过改变固定在每段关节组末端的4 根驱动线的长度而进行控制的。需要建立关节空间变量h、θ和R与驱动空间中各驱动线长度变化量的数学关系。柔性臂中心轴线的弯曲形状为平面内由直线和圆弧组成的曲线,驱动线的形状与柔性臂中心轴线相同,且柔性臂中心轴线与驱动线之间存在位置偏移量,故它们的圆弧段半径不同。因此各驱动线长度变化量 ∆lij为
式中lij为个驱动线长度,i为关节组序号,i=1,2,3,j为驱动线的序号,j=1,2,3,4,下同。
如图4 所示,在全局坐标系O1中的x1-O1-y1平面,柔性臂本体中心轴线以单圆弧曲线的形状弯曲,其末端位置点为EO1(xe,ye,0) ( 即角度φ= 0)。

图4 单圆弧弯曲驱动线示意图Fig.4 Schematic diagram of single arc bending driving lines
以第三段关节组为例,l31、l32、l33和l34分别表示第三段关节组的4 根驱动线长度。根据几何分析可得第三段关节组中各驱动线的长度为:
式(15)中di j为驱动线过孔到坐标轴z1的最短直线距离。如图5 所示,当末端位置点EO2(xe,ye,ze)未在平面x1-O1-y1内(即角度φ≠0)时,坐标系O2的坐标轴z2与 坐标轴y2可视为平面y1-O1-z1中的两条直线。
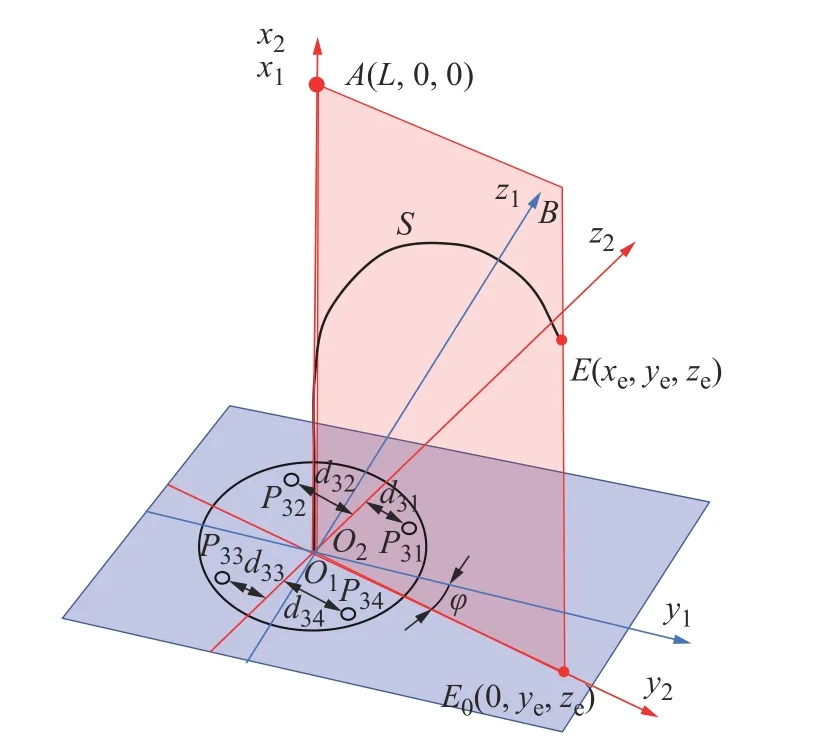
图5 柔性臂驱动线几何关系图Fig.5 Geometric relationship of flexible arm driving lines
各驱动线过孔在平面y1-O1-z1中的投影点为Pi j(0,yi j,zij) 。 如图5 所示,di j可由点Pij到坐标轴z2直线的最短直线距离求得,即
联立式(14)~式(16),即可得到第三段关节组4 根驱动线长度的变化量。由于柔性臂本体弯曲运动时并非每段关节组都弯曲呈圆弧状,在计算第一和第二段关节组驱动线长度变化时,首先分别比较h与2La、La关系,然后根据式(9)求得当前关节组的弯曲角度 θ′,利用式(14)和式(15)即可求得当前关节组4 根驱动线长度的变化量,即柔性臂关节空间至驱动空间的映射关系。连续型柔性臂驱动空间至关节空间分析为根据3 段关节组驱动线长度变化量求解关节变量h、 θ和R,联立式(15)与式(16)可以直接求解。
4 双圆弧曲线的运动学模型
在连续型柔性臂运动过程中存在关节组极限弯曲角度限制,使得在靠近柔性臂本体的目标点处单圆弧曲线无法拟合柔性臂实际弯曲形状。针对此问题可采用双圆弧曲线。双圆弧曲线由直线段H、圆弧段L1和 圆弧段L2组成,其中圆弧段和圆弧段弯曲方向相反,关节空间中的变量H、 θ1、R1、 θ2和R2,如图6 所示。根据柔性臂的驱动结构与理论假设,每段关节组由4 根驱动绳独立控制,使得每段关节组只能产生单圆弧弯曲运动。为更准确的拟合柔性臂实际弯曲形状,将双圆弧曲线的直线段H、圆弧段L1和 圆弧段L2分配到每段关节组。直线段H和圆弧段L1拟 合第一段关节组弯曲形状,圆弧段L2拟合第二和第三段关节组弯曲形状。
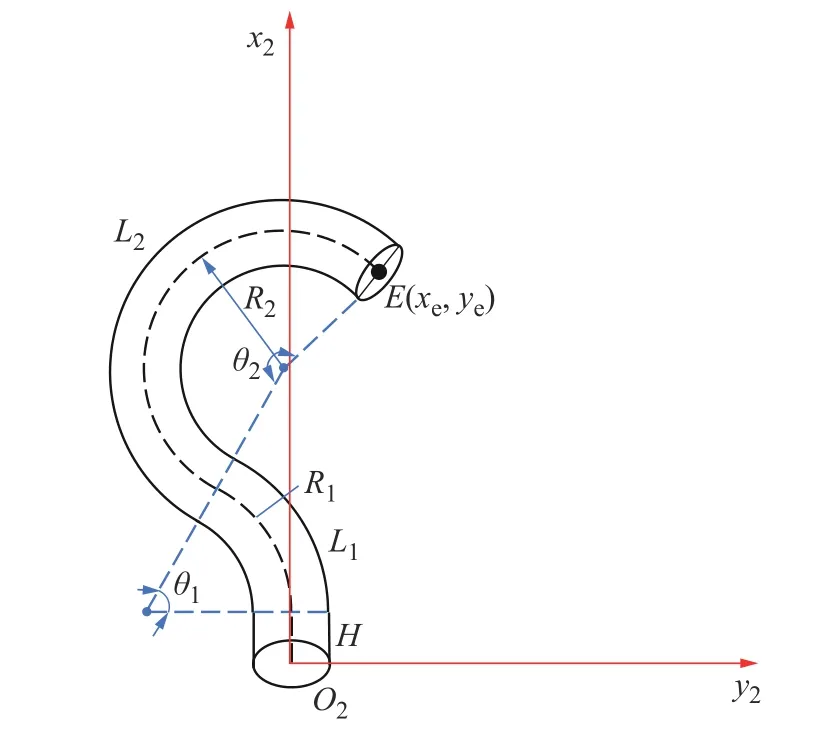
图6 柔性臂双圆弧弯曲运动几何模型Fig.6 Geometric model of double circular arc bending motion of a flexible arm
关节空间至操作空间的运动学映射关系即为已知关节变量H、 θ1、R1、 θ2和R2,求解柔性臂末端位置,如图7 所示。
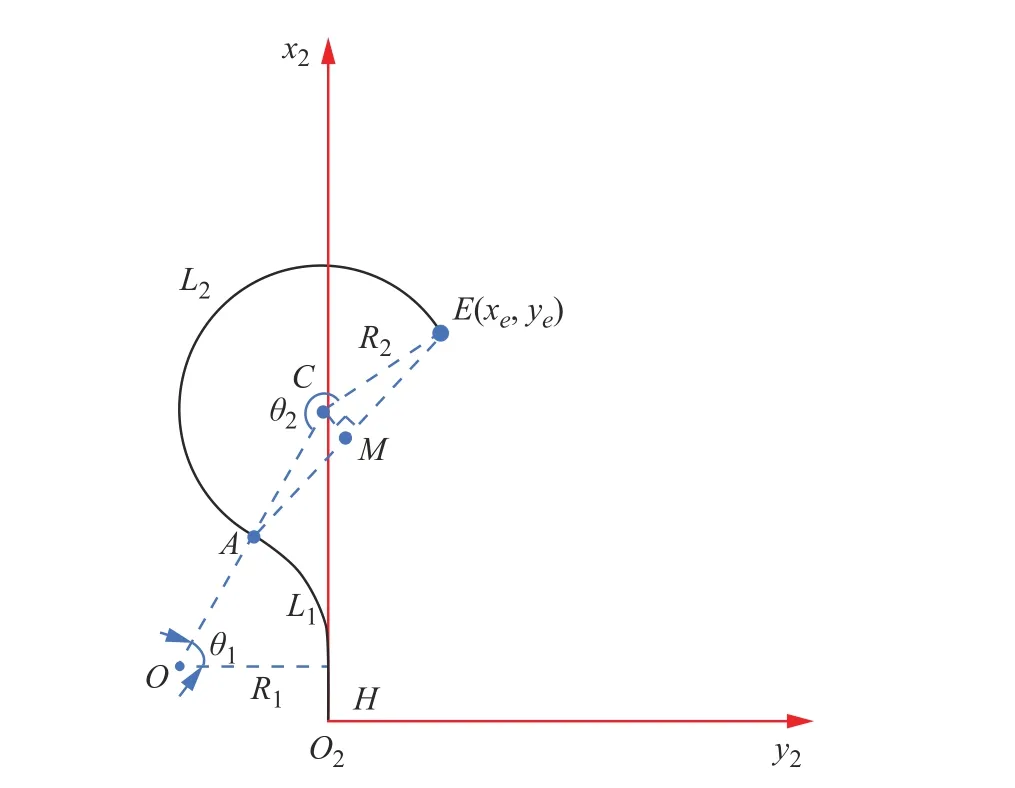
图7 双圆弧曲线几何关系示意图Fig.7 Schematic diagram of geometric relationship of double arc curves
4.1 操作空间与关节空间的运动学分析
根据几何约束可得:
式(17)和式(18)表示关节空间至操作空间的运动学映射关系。操作空间至关节空间的逆运动学分析则是在已知末端位置的情况下,对关节变量H、θ1、R1、 θ2和R2进行求解。根据图7 中的几何约束,得出关节变量之间的数学关系,减少求解参数数量,降低计算难度。其中关节空间变量与长度L的数学关系为
图7 中,设圆弧段L1的末端为点A,线段AE的中点为点M,圆弧段L1的 圆心点为O,圆弧段L2的圆心点为C,直线MC垂直于线段AE,关节变量H、θ1和R1已 知。那么点O的位置为 (H,-R1),点A的位置为 (H+R1sinθ1,-R1+R1cosθ1),可以得出直线OC的表达式为

直线OC与直线MC相交于点C,因此联立式(20)和式(24),求得点C的坐标xC和yC。结合平面内圆弧曲线的弦长公式与几何约束可得:

式(27)为R1关 于 θ1的几何约束关系。只需对独立参数 θ1进 行一维搜索,采用二分法进行求解。 θ1为第一段关节组的弯曲角度,决定着柔性臂的运动范围大小, θ1的 搜索区间为( 0,π/2]。在柔性臂系统运动测试时,为保证弯曲运动过程中末端位置的准确性,靠近驱动机构的柔性臂部分不产生弯曲运动,设定变量H=L/20。
在实际工作中,应用目标点坐标作为末端抓手的位置坐标求解关节空间变量。如图8 所示,目标点TO2(xt,yt,zt)为末端抓手位置。
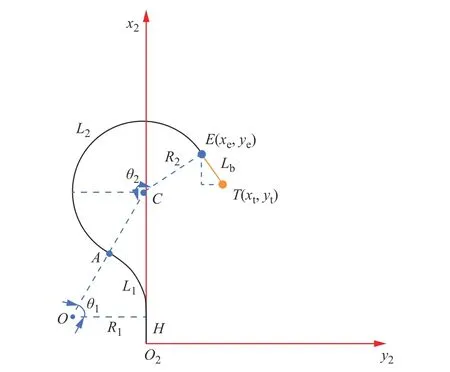
图8 双圆弧曲线形状下末端执行器几何模型Fig.8 Geometric model of an end effector in double arc curve shape
根据几何关系可得点TO2与点EO2的位置关系为:
式中Lb为柔性臂末端到执行器抓取中心的位置点的距离,Lb=110 mm。在实际工作中进行逆运动学解算时,为使得计算结果具有有效性与实用性,只需再计算式(28)和式(29)。
4.2 关节空间与驱动空间运动学分析
当柔性臂中心轴线以双圆弧曲线弯曲时,其关节空间与驱动空间的映射关系和单圆弧曲线运动学模型相似,需将式(15)替换为
5 工作空间分析
工作空间是连续型机器人末端点所能达到的位置的集合。基于上述运动学模型并结合连续型柔性臂的结构参数和关节弯曲角度范围,可遍历计算出柔性臂的工作空间。本文分别对单圆弧曲线和双圆弧曲线的柔性臂弯曲形状进行工作空间仿真分析。设平面B的旋转角 φ的 范围为 [0,2π],当柔性臂以单圆弧曲线弯曲时,可用式(4)和式(5)进行分析,其关节变量具体约束范围如下:
当柔性臂以双圆弧曲线弯曲时,可采用式(17)和式(18)进行分析,其关节变量具体约束范围如下:根据上述范围可分别确定连续型柔性臂末端点的空间位置范围,并采用软件MATLAB 分别绘制其工作空间。图9a)、图9b)分别为平面内单、双圆弧曲线弯曲时柔性臂工作空间;图9c)为柔性臂以单圆弧曲线弯曲和双圆弧曲线弯曲时三维工作空间范围。
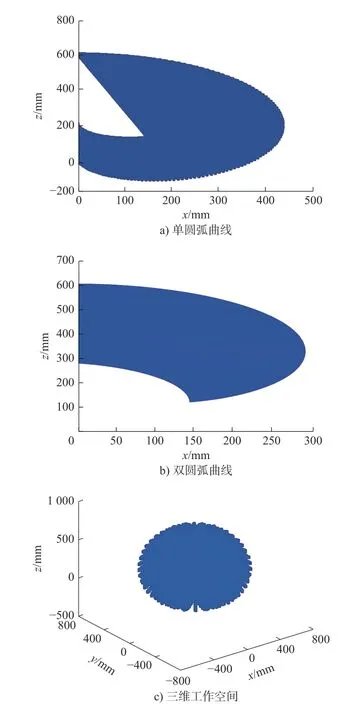
图9 柔性臂工作空间示意图Fig.9 Diagram of flexible arm workspace
根据仿真结果,在平面内单圆弧曲线和双圆弧曲线工作空间具有互补性和重叠性,结合两种方式可达到平面B内柔性臂结构尺寸约束下任意目标点,再结合平面B旋转角 φ的范围,可实现柔性臂优越的空间可达性;当目标点位于重叠区域时,从计算效率来看,应优先选择单圆弧曲线的求解方法。
6 仿真结果与样机实验
6.1 运动学仿真与实验
基于本文的运动学理论模型和柔性臂结构参数,在软件MATLAB 中分别进行单圆弧曲线和双圆弧曲线运动学模型仿真,并制造连续型机器人原理样机,将仿真结果在原理样机上进行实验验证。在初始状态下,柔性臂呈水平悬臂状态并且不发生弯曲,柔性臂末端执行器几何中心的坐标位置为[719,0,0]。单圆弧曲线模型弯曲角度θ ∈[4π/3, 2π]时,柔性臂3 段关节组均有弯曲运动,因此在旋转角度 φ ∈[0,2π], 弯曲角度 θ ∈[4π/3, 2π]的范围内,取采样点k=60,在无约束限制下,对柔性臂末端执行器位置和驱动线长度变化量进行仿真。仿真结果如图10 ~ 图12 所示,其中图10 为柔性臂末端执行器位置变化曲线,图11 为柔性臂第一段关节组4 根驱动线长度变化量曲线,图12 为柔性臂第二段关节组4 根驱动线长度变化量曲线。
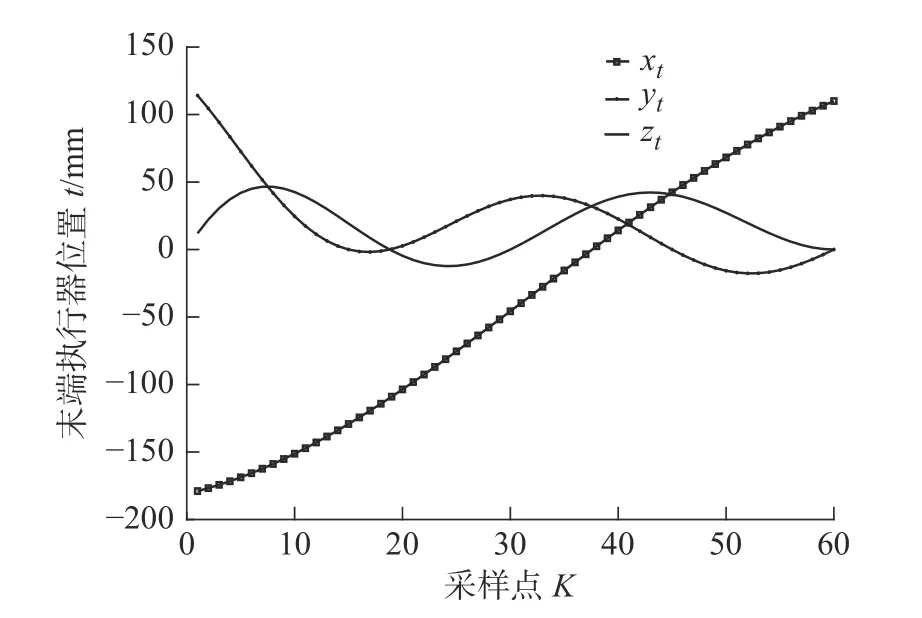
图10 单圆弧曲线柔性臂末端执行器位置变化曲线Fig.10 Position change curve of end effector of a flexible arm with single circular arc curve
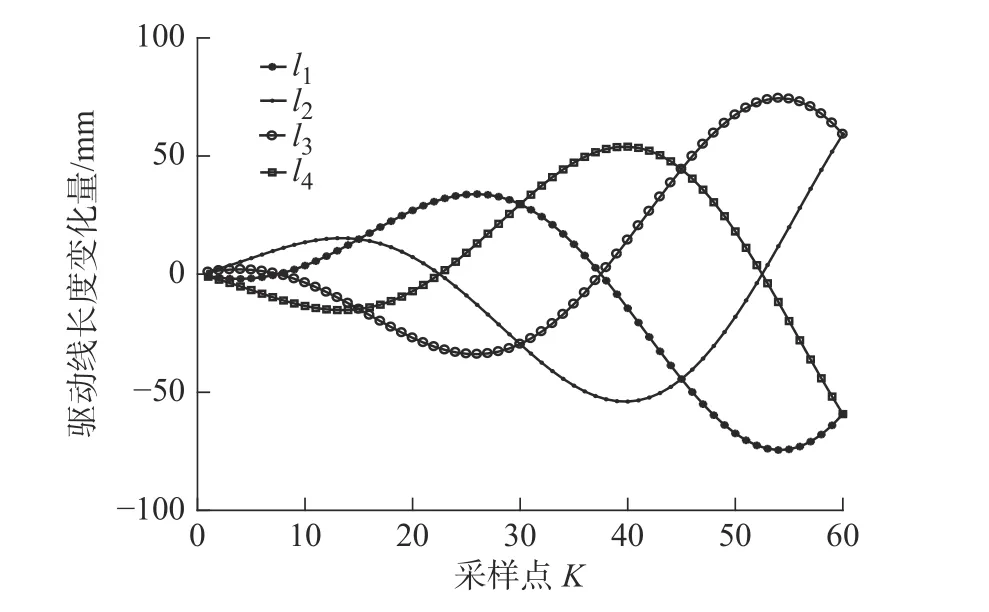
图11 柔性臂第一段关节组驱动线长度变化曲线Fig.11 Length variation curve of driving line of the first joint group of a flexible arm
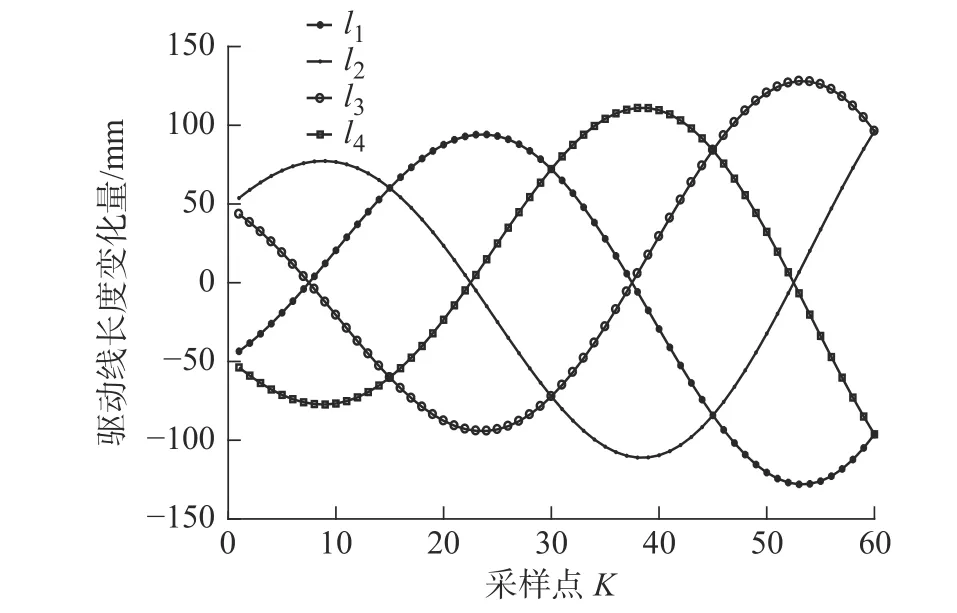
图12 柔性臂第二段关节组驱动线长度变化曲线Fig.12 Length variation curve of driving line of the second joint group of a flexible arm
对于双圆弧曲线运动学模型,在弯曲角度θ1∈[0, π/2],θ2∈[0, 4π/3], 旋转角度 φ ∈[0, 2π]的范围内,取采样点k=60,在无约束限制下,对柔性臂末端执行器位置和驱动线长度变化量进行仿真,图13为柔性臂末端执行器位置变化曲线,图14 为第二段关节组驱动线长度变化曲线。
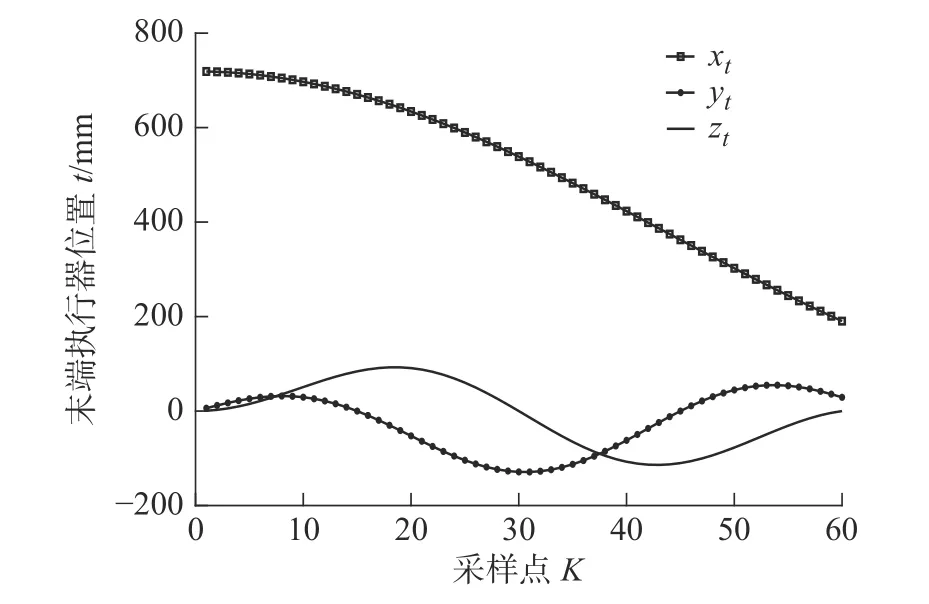
图13 双圆弧曲线柔性臂末端执行器位置变化曲线Fig.13 Position change curve of end effector of double circular arc flexible arm

图14 双圆弧弯曲第二段关节组驱动线长度变化曲线Fig.14 Length change curve of driving line of the second joint group of double arc bending
以单圆弧曲线运动学模型为例,将驱动线长度变化量作为输入量带入运动学模型以及原理样机中,对比柔性臂末端执行器位置的仿真值与实际值的误差。实验分4 种工况进行,其绳长变化量如表1所示,工况1 和工况2 为柔性臂以单圆弧曲线模型弯曲运动,工况3 和工况4 为柔性臂以双圆弧曲线模型弯曲运动,正负号分别代表驱动线拉回和放松。
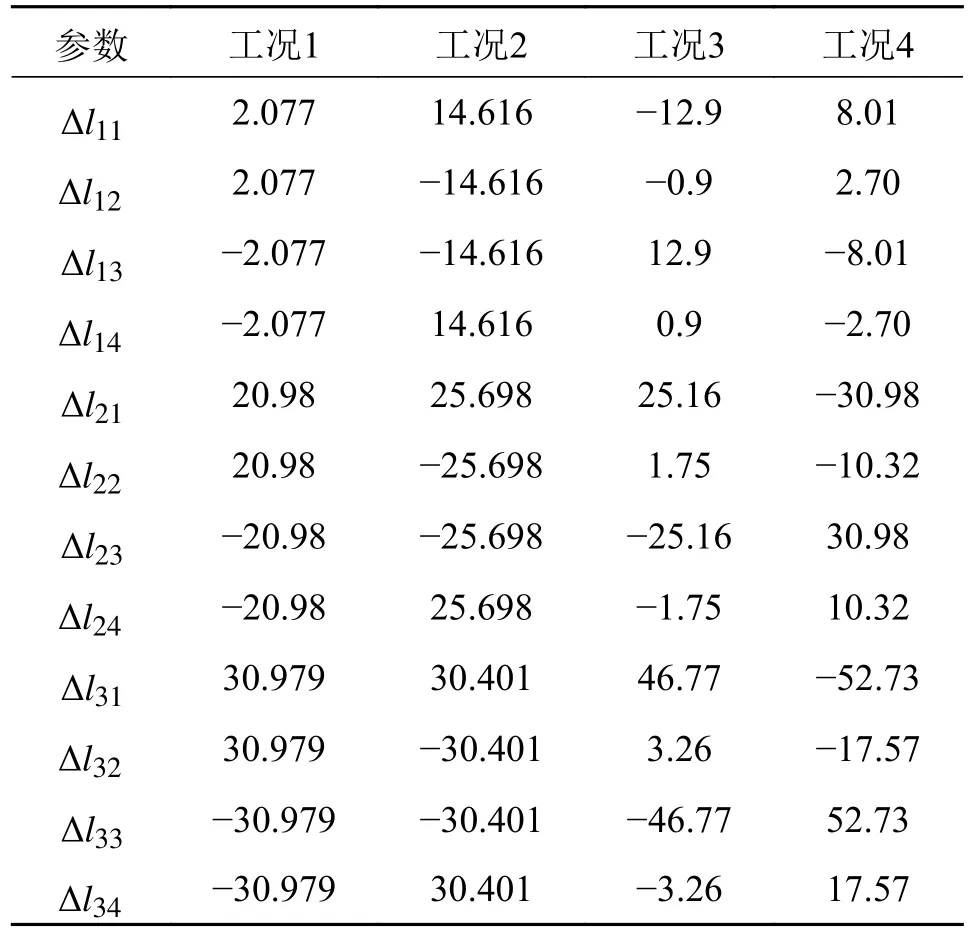
表1 4 种工况下的绳长变化量Tab.1 Rope length variation under four working conditions mm
将表1 数据带入原理样机测量末端执行器实际位置,并与仿真结果进行对比,结果如表2 所示。由表2 可知:4 种工况下柔性臂末端执行器位置的仿真值与实际值的最大误差为10.0 mm,最大相对误差为3.30%,符合当前绳驱动多关节连续型柔性臂的误差范围。对比结果表明,该柔性臂基于平面圆弧法的运动学模型具有正确性和有效性。
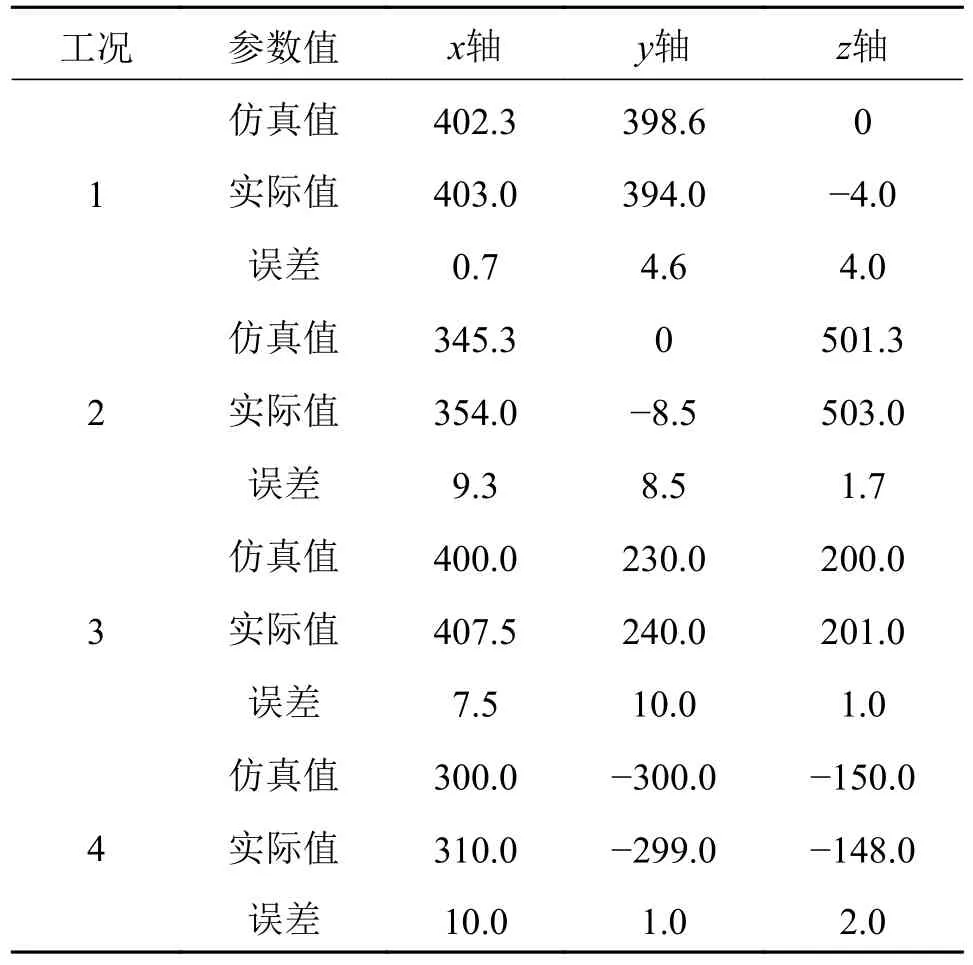
表2 4 种工况下仿真值与实际值Tab.2 Simulation values and actual values under four working conditions mm
为了测试连续型柔性臂在平面内的运动能力,根据本文所提出的运动学模型,利用设计制造的连续型柔性臂系统,分别以单圆弧曲线和双圆弧曲线进行平面内运动试验。试验结果如图15 所示,柔性臂能够以单圆弧曲线和双圆弧曲线在平面内的灵活运动。

图15 连续型柔性臂平面内弯曲运动试验Fig.15 In plane bending motion test of continuous flexible arm
6.2 逆运动学实验
为验证逆运动学求解的有效性和正确性,有必要进行原理样机实验。将空间中的一系列离散点作为柔性臂执行器抓取的目标点进行逆运动学求解,并且在求解得到关节空间变量后,根据关节空间至驱动空间的映射关系解算出驱动线长度变化量。将求解得到的驱动线长度变化量输入原理样机,测量其末端执行器位置,并与离散点位置的理论值进行对比。实验过程为先在柔性臂工作空间内随机取16 个目标点,再在y=345平面的一条光滑连续曲线上以10 为步长取16 个目标点,曲线表达式为
式中x的取值范围为[300,450]。
将以上32 目标点位置信息进行逆运动学求解得到其驱动线长度变化量,并在原理样机中进行弯曲运动测量其末端执行器实际位置数据,计算实际位置与理论位置的直线距离误差e1和e2。e1代表柔性臂工作空间内随机取的16 个目标点实际位置与理论位置的直线距离误差,e2代 表y=345平面内16 个点实际位置与理论位置的直线距离误差。根据e1和e2的值,绘制其误差曲线分别如图16 和图17所示。由实验结果可知,两个实验目标点的实际位置与理论位置直线距离误差均小于14 mm,误差主要由驱动绳受力变形、柔性臂加工装配误差和弹簧的一致性问题导致,从而在弯曲运动时柔性臂形状没有完全符合常曲率假设前提。此外,考虑到柔性臂自身的体积与重量,重力的影响也是误差产生的原因之一。因此,以上误差符合当前绳驱动多关节连续型柔性臂的误差范围,验证了逆运动学算法的有效性。后续工作有必要选择更好的驱动绳、弹簧和柔性臂制造材料,以提高柔顺性和减轻自重。
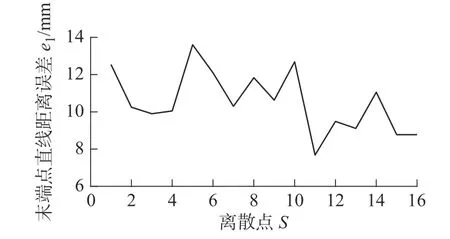
图16 随机取得16 个目标点的直线距离误差曲线Fig.16 Straight line distance error curve of 16 target points at random
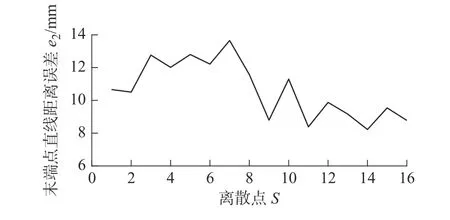
图17 平面y = 345 内目标点直线距离误差曲线Fig.17 Straight line distance error curve of target points in plane y = 345
7 结论
1) 采用平面圆弧法建立连续型柔性臂的运动学模型,分别利用单圆弧曲线和双圆弧曲线拟合柔性臂弯曲形状,建立几何约束关系分析操作空间、关节空间和驱动空间之间的映射关系,并针对逆运动学位置求解得出了一种简便的算法。
2) 对连续型柔性臂运动学算法进行了软件仿真以及原理样机实验,验证了运动学模型的正确性和逆运动学算法的有效性,并展示了连续型柔性臂良好的弯曲运动能力。
3) 平面圆弧法可在平面内拟合连续型机器人的运动位形,结合旋转角φ 使得机器人具有三维空间可达性,满足当前的应用场合。面对更为复杂的应用场景,需要机器人实现空间曲线位形,则为未来的拓展研究工作。
