培养小学生数学思维能力的实践探析

吴丽芳 （福建省仙游县盖尾连井小学）

数学学科既具有严密的逻辑性，还具备高度抽象性。基于这两种特性，学生在学习数学的过程中会感到困难、单调，甚至枯燥。为此，教师要立足小学生的年龄特点和学习规律，引导学生通过表象创设、数形结合等方式直观感知数学知识，不断引导学生通过观察、发现提升“四基”“四能”，促进和发展良好的数学思维能力。

一、激发兴趣，促进自觉思维

1. 激趣，放松心情促思考

教师要结合数学知识和学生特点，通过趣味性的方式营造浓厚的学习氛围，让学生在学习数学知识的过程中放松心情，激发学习数学的兴趣，自觉产生运用数学思维分析和解答问题的热情。例如，在教学人教版《义务教育教科书·数学》（以下统称“教材”）二年级上册“7 的乘法口诀”这节课时，教师可以通过组织“拍7”这一趣味性游戏帮助学生加深对7的乘法口诀的记忆，让全班学生以“开火车”的形式依次由1 数到70，数到7、含有7，以及7 的倍数的学生要拍手，数出错的学生表演一个小节目。随后，举一反三，让学生对8 的乘法口诀、9 的乘法口诀进行练习。通过趣味性的教学方式，学生不再感觉记忆乘法口诀是枯燥乏味的，对学习数学知识充满了兴趣，自主调动数学思维思考问题。

2. 激趣，乐于表达促思维

教师要善于营造轻松、和谐的交流氛围，借助直观的事物促进学生对所学知识进行感性认识，再进行数学算理有序表达的训练，让学生逐渐形成理性认知。例如，在教学教材四年级上册“平行四边形”这节课时，教师可以利用教室和生活中学生所熟知的一些物品，带领学生回想在哪些地方见过平行四边形，并引导他们积极研究、思考有关平行四边形的相关概念和特点。交流反馈时，教师引导学生积极回答问题，清晰地描述自己的理解和感受。有的学生说：“平行四边形的对边互相平行。”有的学生说：“平行四边形的对边也相等。”整节课上，学生的参与热情高涨，在轻松的氛围中不仅锻炼了学生的语言表达能力，还加深了学生对平行四边形这部分内容的感知和理解。更重要的是，通过和谐的课堂氛围和生活化的学习方式，让学生从中获得轻松、愉悦的学习体验，激发了学生的学习兴趣，同时发展了初步的数学思维能力。

二、具体表象，培养形象思维

1. 表象积累，激活学生思维

表象的积累对于学生理解概念、定理、法则等知识内容具有十分重要的促进作用。例如，在教学教材四年级下册“轴对称”这节课时，教学重点是让学生初步认识轴对称现象，并探索轴对称图形的性质与特点。在教学中，教师并没有直接按照教材内容引导学生了解相关的概念，而是给学生提供了一些图片，如京剧脸谱、展开翅膀的蝴蝶、双喜字形状的剪纸等图案，让学生将图片中的图案剪下来，尝试通过折叠、旋转、平移等操作探索图形的特点。经过不断的操作和总结，很多学生都发现沿着这些图案的某条线对折之后，直线两侧的部分可以完全重合。学生结合这一发现对教材内容进行了自主探究和思考，初步积累了轴对称的表象，对轴对称图形的特点有了初步了解。

2. 数形结合，开拓解题思路

数形结合是数学教学培养学生形象思维的重要途径。通过运用数形结合的思想方法，将抽象的内容化为形象，开阔了学生的解题思路，活跃了学生的数学思维。例如，在教学教材五年级上册“数学广角——植树问题”这节课时，教师可以出示题目：在长24米的小路一边栽树，每隔3米种一棵（两端都要栽），一共可以栽几棵树？学生解答后，出现了两种答案：8棵和9棵。此时，教师可以让学生画线段图（如图1）解题，从中发现规律。

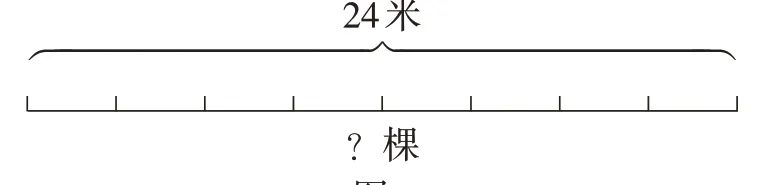
图1

学生通过画图发现当两端都要栽树时，栽树的棵树要比间隔数多1。这样通过数形结合的方式抓住了问题的本质，使学生的思路简明清晰，顺利解决问题。

三、重视想象，发展发散思维

小学数学教学注重发展学生的想象力，让他们学会多思考、多角度看待问题，进而培养发散思维。例如，在教学教材六年级下册“比例的应用”这节课时，教师出示问题：工厂实际每天能够生产250 件产品，比原计划每天生产的件数少了50，这批产品按原计划是3天完成，现在实际生产这批产品需要多少天？教师发现有的学生解题误列等式(250-50)x=250×3。教师把这个等式写在黑板上，并让这名学生说说为什么这样列式，再通过逐步解析和延迟设问的方法反向发问：“你是根据什么数量关系列出这个等式的？等式中的(250-50 )具体表示的是什么？你是怎样理解‘比原计划每天生产的件数少了50’的？(250-50 )能够正确表示出‘比原计划每天生产的件数少了50’这句话吗？要求原计划每天能够生产的产品应该怎样列式？(250+50 )与谁相乘才是正确的？”教师通过引导学生对上述问题的逐步思索、分析，将难点一步步拆解出来，让学生自己去探索分析每一步的含义，使学生在探索、分析中通过理解正确的解题思路，提高思维能力和想象力，培养学生良好的思维品质。

四、巧用迁移，促进思维转化

教师要结合具体的教材内容，立足学生的思维角度，遵循因材施教的原则，帮助学生实现从形象思维到逻辑思维的转化，促进学生的数学知识向更深处蔓延。例如，在教学教材一年级下册“找规律”这节课时，教师可以遵循循序渐进的原则逐步引导学生理解知识，并通过对数学知识的深入理解发散思维，达到举一反三的目的。教师可以借助多媒体呈现如图2 所示的图片，引导学生通过观察图片、发现“一组母鸡和小鸡的个数”的规律。随后，教师可以提出“如果接下来要再出示母鸡和小鸡时，应该是几只母鸡、几只小鸡呢？”的问题，引导学生从中发现规律。

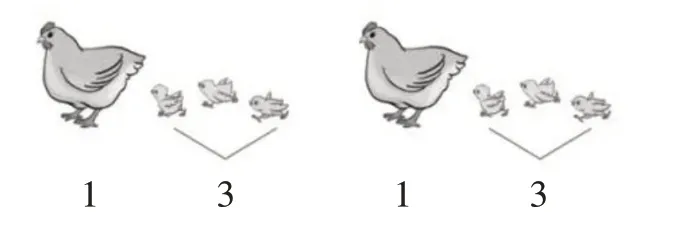
图2

在学生多次练习掌握规律之后，教师可以直接出示练习题，让学生找规律，填数，如“3，6，9，12，（ ）”“11，9，7，5，（ ）”。这样，学生逐渐从形象思维转化为逻辑思维，有效培养了相应的理解能力、推算意识和创新思维。

五、渗透思想，巩固思维能力

将数学思想渗透于小学数学教学中，既可以发展学生的数学思维能力，又可以促进学生问题解决能力的提高。教师应该深入挖掘教学内容中蕴含的数学思想，并将其渗透于学生的学习过程中，进一步强化实际的教学效果，从而发展学生的思维能力。例如，在教学教材三年级上册“分数的初步认识”这节课时，如果直接引导学生理解分数的概念，对于学生来说是比较抽象的。为此，教师可以尝试采用数形结合思想引导学生。教师可以先在黑板上画出一个圆形，用它代表一张饼，并引导学生了解单位“1”的含义。接着，将这张“饼”分成大小相等的2 份，然后指着其中1份告诉学生：“现在一张完整的饼变成了2份，对于其中的任意1份，也就是它的二分之一。”通过这种方式，使“二分之一”这个数量具有了特殊的含义，让学生对“二分之一”有了更加准确的理解。

小学阶段是学生形象思维向逻辑思维过渡的关键时期。教师应该巧用教学策略，创设多样化的教学情境，不断引导学生立足不同角度展开思考和想象，使其切实把握数学本质，循序渐进地达成学习目标，促进学生数学思维能力的发展。