面向时间序列有序分类的Shapelet 抽取算法

杨 骏，敬思远，钟 勇

(1.中国科学院成都计算机应用研究所 成都 610041；2.乐山师范学院电子信息与人工智能学院 四川 乐山 614000；3.中国科学院大学计算机科学与技术学院 北京 石景山区 100049；4.厅市共建智能终端四川省重点实验室 四川 宜宾 644000)

时间序列有序分类（time series ordinal classification, TSOC）是时间序列数据挖掘领域的一项重要任务。该任务旨在训练一个分类器，实现对类别标签有序的时间序列数据的自动分类。与传统时间序列分类[1]任务不同，TSOC 采用错分代价来衡量算法有效性。如在医疗辅助诊断系统中，将危重型病症错分成轻型病症的代价远高于将其错分成重型病症的代价。除了医疗辅助诊断外，本任务在金融投资、气象预测等领域都有重要应用。但目前关于该任务的研究非常少，尚处于起步阶段[2]。

基于Shapelet 的时间序列分类近年来受到学界广泛关注[3-5]。Shapelet 是指时间序列中具有良好分类能力的子序列，最早由文献[6]提出，它采用Brute-Force 算法搜索子序列，并用信息增益（information gain, IG）对其分类能力进行评价，最后利用计算得到的Shapelet 构造决策树。由Shapelet 构造的决策树具有非常好的可解释性。随后，文献[7]提出了ST（shapelet transformation）方法。该方法获得Top-K 个最优Shapelet，然后将原始时间序列转换到新的特征空间并采用传统方法训练分类器，使算法的分类能力大幅提升。但是，上述两类算法都采用暴力方法搜索Shapelet，计算效率低。为解决该问题，文献[8]提出了基于三角不等式的剪枝策略，以及提前计算距离的方法；文献[9]用符号聚合近似（symbolic aggregate approximation, SAX）表示时间序列，采用随机投射技术，计算最优Shapelet 集合；文献[10]提出了基于随机采样的Shapelet 抽取算法；文献[11]提出了基于随机采样的随机Shapelet 森林算法gRSF；文献[12]在上述工作基础上进一步改进，提出了压缩随机Shapelet森林算法CRSF。CRSF 采用SAX 表示时间序列，通过随机采样构建一个高质量的Shapelet 池，然后从池中随机选择Shapelet 生成决策树节点，提升了算法性能。近年来，基于Shapelet 构建深度学习模型也受到学界广泛关注[13-14]，但考虑到深度神经网络可解释性不足，本文不再详细介绍。

文献[15]提出了基于Shapelet 的时间序列有序分类算法。该工作主要提出了两项面向TSOC 的Shapelet 评价指标，Spearman 相关系数和Pearson相关系数。与IG 不同，这两项评价指标通过计算Shapelet 与时间序列的欧式距离和标签距离之间的相关系数来评价Shapelet。实验结果表明，评价指标与IG 相比有效地降低了算法的错分代价。但是，该方法中提出的Shapelet 评价指标都需要计算Shapelet 到时间序列的距离，计算效率较低。

本文提出一种基于覆盖集中度和覆盖优势度的Shapelet 评价指标CD-Cover（concentration and dominance of coverage），以及一种面向时间序列有序分类的Shapelet 抽取算法。该算法采用SAX 表示时间序列，通过随机采样Shapelet，使用CD-Cover指标评价Shapelet，抽取最终的Shapelet 结果集。然后，通过ST 方法将时间序列数据集转换到新的特征空间并训练有序分类器。最后，在UCR 和UEA 时间序列分类资源库[16]挑选适合TSOC 任务的11 个数据集上，采用CCR（correct classification rate）和Weighted-κ 两个指标对所提算法进行了实验验证。

1 相关理论及问题描述

通常，时间序列是按照固定时间间隔采集得到的数值型数据序列，可以表示为X=〈x1,x2,···,xm〉，xi∈R，m为时间序列的长度。进一步，将二元组T=〈X,c〉称为时间序列样本，c是时间序列样本的类别标签（简称标签）。D={T1,T2,···,Tn}为一个时间序列数据集，其中，n称为时间序列数据集的大小。Y={c1,c2,···,cQ}表示时间序列数据集D中所有样本标签的集合，Q是标签数。在TSOC 问题中，要求Q≥3， 且标签之间存在全序关系c1≺c2≺···≺cQ。

时间序列数据通常都是高维实数，不仅需要大量存储空间，而且计算代价也很高。文献[17]提出一种时间序列的SAX 表示方法，将数值型时间序列转换为符号型时间序列，可以达到数据降维、降低噪声、节省存储和简化计算等目的。SAX 表示方法的转换过程如下。

给定时间序列X=〈x1,x2,···,xm〉、动态窗口长度ω 和字母表Σ，将X平均分成段，得到其中为：

传统的Shapelet 是指时间序列的任意子序列，本文的候选Shapelet 是基于SAX 表示的时间序列，下面给出其定义。

定 义 1（候选Shapelet） 给定SAX表示的时间序列，称该时间序列的任意子序列为一个候选Shapelet，其中b和l分别表示候选Shapelet 在时间序列中的开始位置和长度，且

基于Shapelet 的时间序列分类，核心是找出最具代表性的候选Shapelet 集合，称为Shapelet 抽取。

文献[6]最早采用IG 对Shapelet 的分类能力进行评价。IG 也是当前研究和实践中最常用的Shapelet 评价指标。文献[7]提出了Kruskal-Wallis、F-statistic 和Mood's median 这3 种指标，并通过实验证明了其有效性。但上述指标没有考虑错分代价，在TSOC 任务中表现不佳。文献[15]提出了Spearman 相关系数和Pearson 相关系数两项指标，充分考虑了类别有序这一特征。但是，两项指标都需要计算Shapelet 到时间序列之间的距离，计算成本较高。

2 面向TSOC 的Shapelet 抽取算法

2.1 分类算法框架

本文设计的面向时间序列有序分类算法框架如图1 所示。首先，采用SAX 方法将数值型时间序列数据集转化为符号型时间序列数据集。然后，采用随机采样+布隆过滤+Shapelet 评价的策略，实现对Shapelet 的抽取。其中，随机采样+布隆过滤旨在提升算法效率以及进行预剪枝。该策略在文献[18]中已被验证有效。本文提出一种新的面向SAX 表示时间序列有序分类的Shapelet 评价指标CDCover。图1 中图标表示是否满足约束条件，如果不满足约束条件，继续采样和评价，否则，结束采样评价。接下来，算法对抽取出的Shapelet 进行自相似移除，降低特征冗余度。最后，选取指定大小的Shapelet 集合作为数据集的新特征，使用新特征对原始时间序列进行特征空间转换，并训练有序分类器。

图1 面向时间序列有序分类算法框架

2.2 Shapelet 评价指标CD-Cover

为提升Shapelet 评估效率，本节介绍一种适用于时间序列有序分类的Shapelet 评价指标CDCover。首先，给出覆盖、覆盖集中度和覆盖优势度的定义。

定 义 2 （覆盖） 给定一个SAX 表示的时间序列数据集和 一个Shapelets，的标签数为Q， 称 Φ(s)=〈λ1,λ2,···,λQ〉为s在上的覆盖。其中， λi为包含s的ci类时间序列样本数。

定 义 3（覆盖集中度） 给定Shapelets在时间序列数据集上的覆盖Φ (s)=〈λ1,λ2,···,λQ〉，Q为的 标签数。则s在上 的覆盖集中度c on(s)定义为：

式中， V ar(Φ(s))为 Φ(s)的 方差； Varmax为方差上界。根据方差性质可知，当覆盖取值平均分布在值域两端时取得最大值/，因此覆盖集中度的方差上界Varmax=(1-Q)24。从上述定义容易看出，con(s)取值范围为[0,1]，值越大，表明覆盖的方差越小，覆盖越集中。特殊情况下，如果s仅覆盖一类时间序列，则方差为0， c on(s)值 为1；如果s仅覆盖类别标签最小和类别标签最大的时间序列，且覆盖比率相同，则方差达到上界，c on(s)值为0。

换言之，覆盖优势度为类别最高覆盖率与次高覆盖率之差。覆盖优势度d om(s)的取值范围是[0,1]，值越大，表明覆盖的优势越明显。如果Shapelets仅覆盖一个类别的时间序列，则覆盖优势度为该类类别的覆盖率。

定 义 5（CD-Cover） 给定Shapelets和时间序列数据集D︿，s在D︿上的覆盖集中度和覆盖优势度分别为c on(s) 和 d om(s)， 则s的CD-Cover 评价值为：

式中， α是权重因子，用来调节覆盖集中度和覆盖优势度的权重，默认两者权重相同，即α 取0.5。如果覆盖集中度越高，则 c on(s)值越大；如果覆盖优势度越大，则 dom(s)越 大，并且， σ(s)取值范围为[0,1]。因此，如果CD-Cover 值越大，表明其分类能力越强。

下面，通过4 个算例来展示CD-Cover 指标的计算过程及其有效性。

算例1 时间序列数据集D︿ 标 签Y=〈1,2,3,4〉，即Q=4， 且每类时间序列样本数分别为 〈 5,5,2,2〉。如果给定一个Shapelets1， 且s1在 数据集上的覆盖Φ(s1)=〈4,1,0,0〉。 则计算可得， Var(Φ(s1))=0.17，而Varmax=(1-4)2/4=2.25， 所以，s1的覆盖集中度con(s)=1-0.17/2.25=0.924。根据定义4，覆盖率为Π(s1)=〈4/5,1/5,0/2,0/2〉，因此，类别1 覆盖率最高为0.8，类别2 覆盖率次高为0.2。所以，覆盖优势度d om(s1)=0.8-0.2=0.6。根据式（4），计算s1的 CD-Cover 为σ(s1)=0.5×0.924+(1-0.5)×0.6=0.762。

算例3 算例1 相同的时间序列数据集D︿中，如果给定Shapelets3， 在上 的覆盖Φ (s3)=〈1,1,0,0〉，则Var(Φ(s3))=0.125， con(s3)=1-0.125/2.25=0.944；s3在上的覆盖率Π (s3)=〈1/5,1/5,0/2,0/2〉，覆盖优势度为d om(s3)=0.2-0.2=0 。 因此，s3的CD-Cover值为σ (s3)=0.5×0.944+(1-0.5)×0=0.472。

通过以上算例可以发现，CD-Cover 的目标是找出最优的Shapelet。这些Shapelet 覆盖的时间序列集中在某个类别附近，且对该类时间序列有很高的覆盖比例。如果Shapelet 覆盖且只覆盖一个类别的所有时间序列，其CD-Cover 值为1。

2.3 基于随机采样的Shapelet 抽取算法

基于随机采样的面向时间序列有序分类的Shapelet 抽取算法核心步骤算法如下。

算法第1 行：根据参数 ω和 Σ将原始时间序列训练集D转换为SAX 表示的时间序列训练集。

算法第2、3 行：初始化Shapelet 结果集合S和布隆过滤器BF。本算法采用布隆过滤器检索当前候选Shapelet 是否已经出现并评价，如果此前已经出现则不再进行评价，提升算法效率[18]。

算法第4 行：进入循环，当计时器超过限定时间，结束Shapelet 抽取。

︿D算法第5、6 行：随机从 中选择一条时间序列，然后从该时间序列中随机抽取一个候选Shapelet。

算法第7、8 行：通过布隆过滤器判断Shapelets是否已经出现；如果已出现，则跳过CD-Cover值计算，重新进行Shapelet 采样。

算法第9、10 行：更新布隆过滤器，并计算候选Shapelets的CD-Cover 值。

算法第11、12 行：判断当前候选Shapelets的CD-Cover 值是否大于给定阈值ε，只有评估值大于ε，才将其加入S，保证抽取高质量Shapelet。

算法第13、14、15 行：判断抽取得到的Shapelet 集合大小是否大于预设数目N的两倍，如果满足条件，则从S中移除CD-Cover 值最小的候选Shapelet，同时将阈值 ε更 新为S中Shapelet 的最小CD-Cover 值。保留预设数N两倍数量的候选Shapelet 是后续还要从中移除自相似的Shapelet。

算法第16 行：首先从S中移除自相似的Shapelet。自相似Shapelet 指的是两个候选Shapelet取自同一条时间序列，且存在重叠部分。大量自相似的Shapelet 会造成特征空间冗余，降低算法分类效果。移除自相似Shapelet 的算法在文献 [12,19]中均有介绍。最后，返回剩余候选Shapelet 中CDCover 值最高的N个Shapelet。

2.4 时间复杂度分析

如果时间序列数据集D 的大小为n，所包含的时间序列长度均为m，SAX 窗口大小为 ω。则经过转换，采用SAX 表示的时间序列数据集D︿中包含n条字符形时间序列，每条长度均为t=「m/ω■。

在上述算法中，将原始时间序列转换为SAX表示时间序列的时间复杂度为O(nm)（第1 行），移除自相似算法的时间复杂度依赖于候选Shapelet的数量，该数量远小于时间序列数据集的大小n与长度m的乘积nm。因此，第1 行和第16 行的时间复杂度合计为O(nm)。

本文采用的随机采样框架设置了Shapelet 评价时间限制，通常应采用单位时间内的吞吐量来分析算法性能。但是，反过来，也可以通过分析抽取单个候选Shapelet 的时间复杂度来评价算法性能。Shapelet 抽取算法的主要时间开销为CD-Cover 值计算，需要判断候选Shapelet 是否存在于某条时间序列中。本文采用KMP 算法，其最坏时间复杂度为O(t)。在n条时间序列中进行字符串匹配，其最坏时间复杂度为O(tn)。该时间复杂度明显低于文献[15]提出的Spearman 相关系数和Pearson 相关系数的时间复杂度。换言之，在相同时间约束内，本文提出的算法抽取和评价的Shapelet 数量要远多于文献[15]提出的算法。

3 实验与分析

为了验证所提Shapelet 抽取算法的有效性，在公开数据集上进行实验，训练生成有序分类器，并采用不同指标来评价这些分类器的分类能力。

3.1 实验准备

3.1.1 实验环境和数据集

实验硬件配置为Intel Xeon Gold 5215 CPU（2.5 GHz 主频，8 核）和64 GB 内存。操作系统为Windows Server 2016。实验工具采用Python3.6.8、时间序列挖掘工具包sktime 0.9.0 和有序分类开源框架ORCA（ordinal regression and classification algorithm）[20]。ORCA 的运行环境为MATLAB 2018b。

从时间序列分类资源库UCR 和UEA[16]，根据以下条件筛选出11 个实验数据集：1）类别标签之间有明确的全序关系；2）类别数不小于3；3）时间序列长度相等。数据集的基本信息如表1 所示。

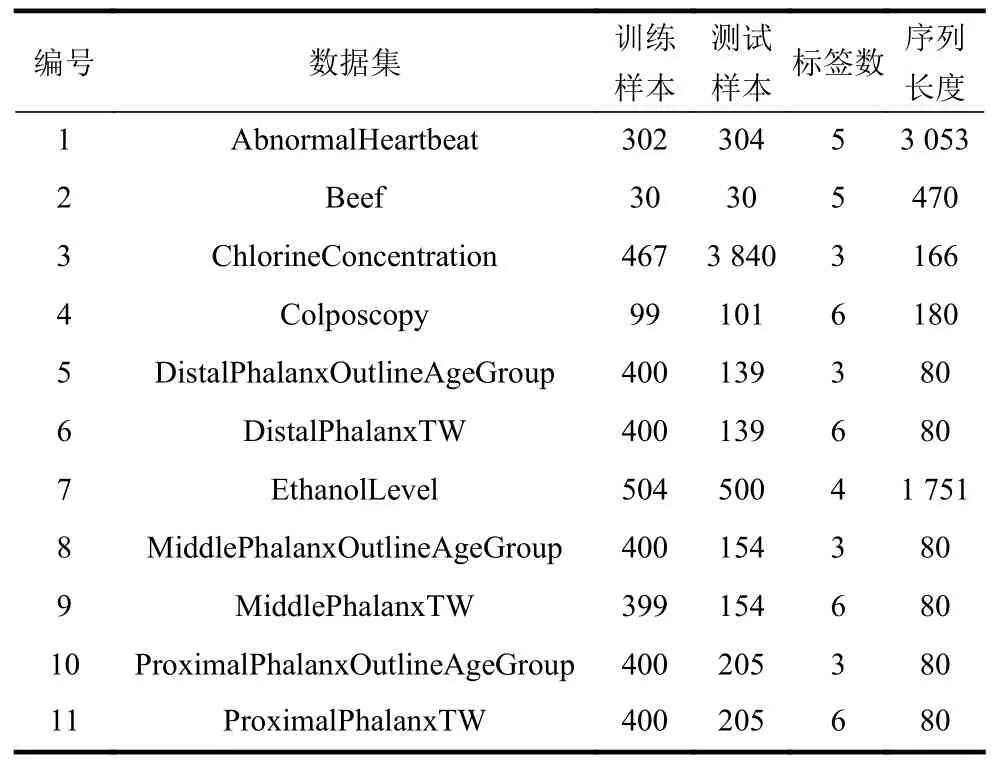
表1 实验数据集

3.1.2 有序分类器和评价指标

传统ST 方法将抽取的Shapelet 用于训练标准分类器，如支持向量机、随机森林等。但标准分类器没有考虑类别标签有序的问题。实验采用了3 种有序分类研究中常用的分类器SVC1V1[21]、SVOREX[22]和SVORIM[22]来验证本文所提Shapelet抽取算法。其中，SVC1V1 是标量分类器，SVOREX和SVORIM 是有序分类器，这些分类器的实现均来自ORCA 开源框架[20]。

实验采用CCR 和Weighted-κ 作为分类器分类能力的评价指标。前者是最常用的分类评价指标，但没有考虑类别标签有序的特征；后者是目前研究验证的、更适用于评价有序分类能力的指标[23]。CCR和Weighted-κ 分别由式（5）和式（6）计算所得。

式中，n是时间序列测试集大小；ci和分别表示测试集中时间序列样本Ti的实际标签和分类器预测标签； δ (ci,)是 Kronecker 函数，当且仅当ci和相同时，函数值为1，否则函数值为0。CCR 取值范围为[0,1]，值越大，表明分类器性能越好。

Weighted-κ 取值范围为[-1,1]，值越大，表明分类器的分类效果越好。

3.1.3 实验参数设置

实验中，本文提出的Shapelet 抽取算法的参数设置如表2 所示。其中CD-Cover 计算公式中的权重因子α 设置为0.5，换言之，设定覆盖集中度和覆盖优势度有同等的重要性；Shapelet 抽取过程中根据候选Shapelet 的CD-Cover 值是否大于初始阈值ε决定是否对其保留， ε设置为0.5。此外，SAX 的参数 ω和 Σ分别设置为1 和10。这样设置有两个理由：1）文献[12]通过实验证明该设置在大部分数据集上能取得较好的分类结果；2）本文主要是利用SAX 的符号表示能力，即将数值型时间序列转换为符号型时间序列，并不特别关注其对数据的维度约减能力。此外，训练有序分类器的时候，3 种支持向量分类器的惩罚参数和核函数参数都设置为相同的搜索范围 {10-3,10-2,···,102,103}，并采用5 折交叉验证，搜索最优参数组合。时间约束 τ设定为300 s。

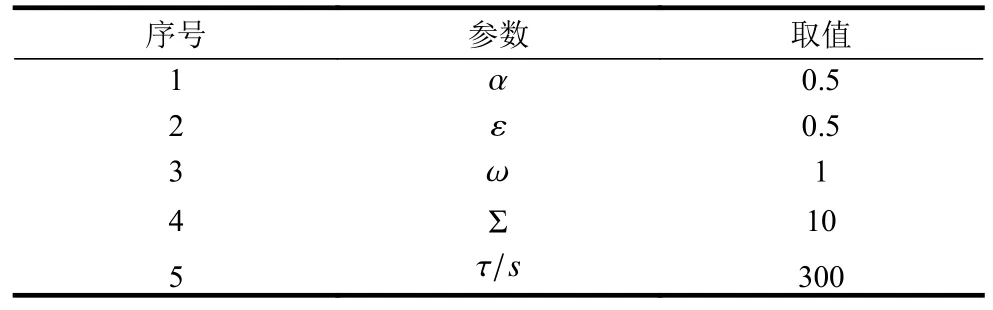
表2 实验参数设置

3.2 实验结果

本节首先验证所提CD-Cover 指标的有效性。实验将根据IG、Spearman 相关系数、Pearson 相关系数和CD-Cover 4 种评价指标抽取的Shapelet，分别用来训练3.1.2 节中的3 种分类器，然后比较4 种指标在实验数据集上的有序分类效果。由于算法具有随机性，为保证结果的公平性，CCR 和Weighted-κ 结果都取50 次实验的平均值。

1）CCR

采用3 种分类器SVC1VC、SVOREX 和SVORIM 在11 个数据集上进行实验，得到的CCR 结果如表3 所示，表中IG、 ρ、 γ和 σ分别代表IG、Spearman 相关系数、Pearson 相关系数和CD-Cover指标。对每个数据集而言，同一分类器不同指标的CCR 最高值用粗体标注。表格最后的“胜出”，表示采用当前分类器的4 种Shapelet 评价指标中，各指标在11 个数据集上取得CCR 最优分类结果的数据集个数。如采用SVC1V1 分类器结合IG 评价指标，分别在第2、第6 和第9 个数据集上取得3 次最优分类结果。“排名”表示采用当前分类器的4 种Shapelet 评价指标中，各指标在11 个数据集上取得的CCR 值的平均排名。例如，采用SVORIM 分类器结合Pearson 相关系数，在11 个数据集上的平均排名为2.55。CD-Cover 指标在3 种分类器上“胜出”的数据集都是6 个（超过数据集的半数），且在3 种分类器上的平均排名都最高，分别为1.77、1.91 和1.86。

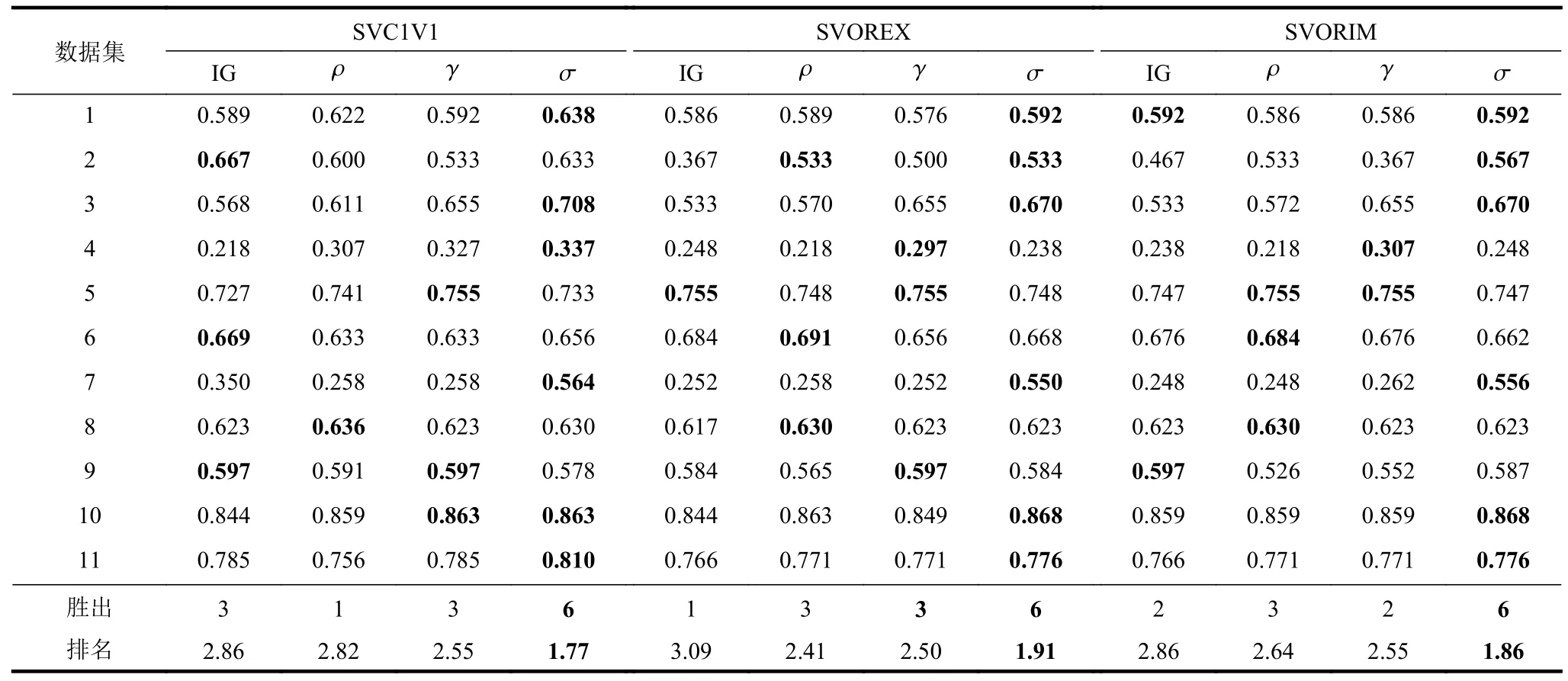
表3 不同Shapelet 评价指标的CCR 值

2）Weighted-κ

表4 给出了采用3 种分类器结合4 种Shapelet评价指标在11 个数据集上获得的Weighted-κ 结果。由表4 可知，在11 个数据集上，CD-Cover 指标在3 种分类器上分别取得了6 次、6 次和7 次最优的表现。同时，CD-Cover 指标在3 种分类器上都取得了最高的平均排名，分别为1.77、1.64 和1.50。

表4 不同Shapelet 评价指标的Weighted-κ 值

3.3 实验分析

为了更清晰地对实验结果进行分析，将3.2 节的实验数据绘制为散点图，如图2 所示。3 个散点图分别代表CD-Cover 与IG、Spearman 相关系数和Pearson 相关系数在3 种算法、11 个数据集上“一对一”比较的结果，每个散点图中散点数目合计33 个。图2 的横坐标和纵坐标分别表示采用CD-Cover 指标与对比指标得到的CCR 值。散点如果正好处于对角线上，表明采用两种指标得到的CCR 值相同；如果散点处于对角线右下方，表明采用CD-Cover 指标得到的CCR 值更优；如果散点处于对角线左上方，表明采用对比指标得到的CCR 值更优。从图2 可以发现，大多数散点处于对角线右下方，或者在对角线附近；明显处于对角线左上方的散点数目较少。

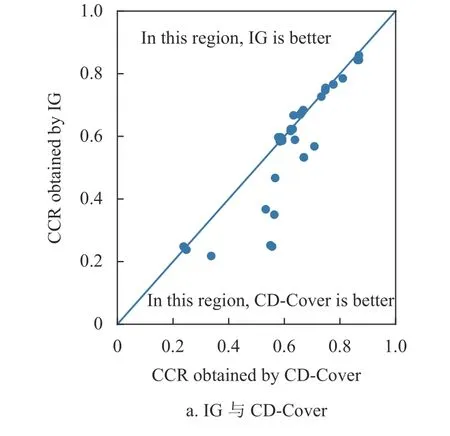
图2 CD-Cover 与3 个指标的CCR 值比较

图3 为采用CD-Cover 指标与采用3 个对比指标得到的Weighted-κ 值对比结果。图3 的横坐标和纵坐标分别表示采用CD-Cover 指标与对比指标得到的Weighted-κ 值。可以发现，图3 的大多数散点都处于对角线右下方区域，且相对图2 而言，偏离对角线更明显。图2 和图3 表明，与采用的3 种对比指标相比，CD-Cover 指标无论是CCR 还是Weighted-κ，都能得到更好的结果。

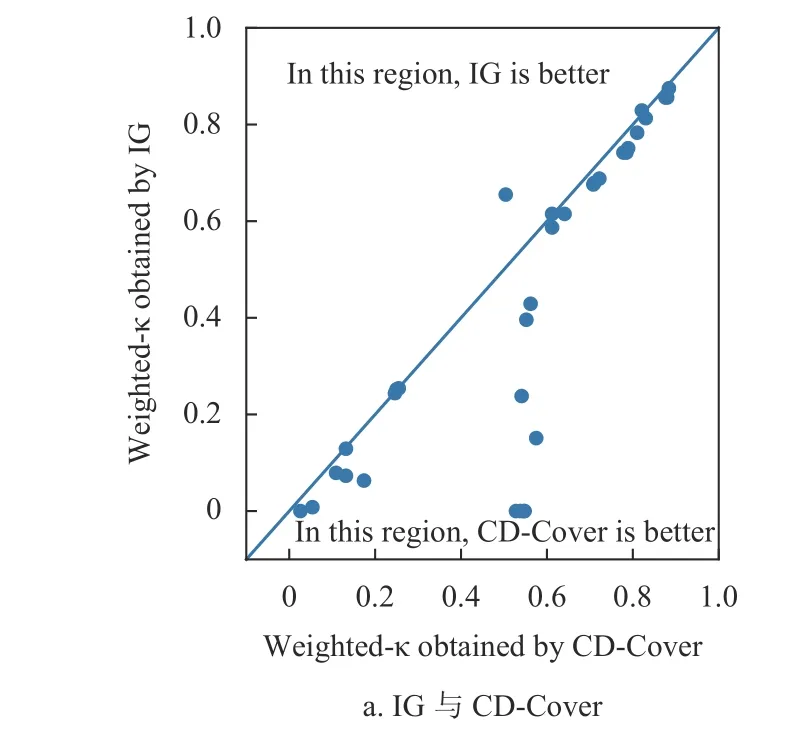
图3 CD-Cover 与3 个指标的Weighted-κ 值比较

3.4 计算效率分析

参与比较的仍然是3.3 节的4 种评价指标。区别在于，IG、Spearman 和Pearson 相关系数不需要将原始时间序列进行SAX 表示。有序分类器只选择SVORIM 分类器，分类器的评价指标选择Weighted-κ。基于不同Shapelet 评价指标的Shapelet抽取算法均持续运行20 min，并记录下每分钟的Weighted-κ 值。为保证稳定性，实验结果为50 次实验的均值，结果如图4 所示。

图4 的每个子图4a～图4k 分别对应单个数据集的实验结果。所有子图的横坐标均表示Shapelet抽取算法的执行时间（min），纵坐标表示基于不同评价指标抽取的Shapelet 训练的SVORIM 分类器，在测试数据集上获得的Weighted-κ 值。分析图4 可以发现：1）在不同执行时间内，基于CDCover 指标抽取Shapelet 训练分类器的结果，整体上优于其他3 种评价指标；2）基于CD-Cover 指标抽取Shapelet，在较短时间内就能获得高质量的抽取结果（Colposcopy 数据集为8 min，其余数据集均为2～5 min）。根据上述实验结果可知，本文所提的CD-Cover 评价指标在计算效率上明显优于其他3 个评价指标，因为给定相同时间限制，基于CD-Cover 指标的方法能够评估更多的Shapelet。

4 结 束 语

针对当前基于Shapelet 的时间序列有序分类研究中，采用Spearman 相关系数和Pearson 相关系数进行Shapelet 抽取时计算效率较低的问题，本文提出了一种基于SAX 表示时间序列的Shapelet 评价指标CD-Cover，以及一种基于随机采样的Shapelet 抽取算法。在11 个时间序列数据集上进行了实验。实验结果证明了CD-Cover 评价指标以及所提Shapelet 抽取算法的有效性，且展示了其在计算效率上的优越性。下一步将继续研究时间序列长度不相等的情况，并将算法扩展至多元时间序列，并结合实际应用对时间序列有序分类问题进行深入研究。