基于量子判别分析法的量子连续投资组合优化算法
2023-12-06陈柄任袁淏木吴涵卿李晓瑜
陈柄任,袁淏木,吴涵卿,吴 磊,李 鑫,李晓瑜
(1.建信金融科技有限责任公司 上海 浦东区 200120;2.四川元匠科技有限公司 成都 611730;3.电子科技大学信息与软件工程学院 成都 610054)
随着量子计算的发展,其在解决特定问题时的量子优越性正在体现出来。在理论方面,Shor 算法[1]在解决大素数分解问题时可以实现指数加速,这给现代密码行业造成了冲击。Grover 算法[2]可以二次加速数据库中的搜索问题。在实验方面,谷歌悬铃木超导量子计算机首次实现量子计算优越性。而中国科学技术大学的“祖冲之号”[3]和“九章号”[4]分别在超导和光量子计算机上进一步提升了性能。“祖冲之号”进行1.2 小时的取样任务需要超算花费8 年[3],而“九章号”的取样速度比经典计算机快1 024倍[4]。
现代金融学在解决一些特定任务时,需要极大的算力。这些算力主要被用于对历史数据的分析、高频交易、金融衍生品定价、投资组合优化以及风险管理等领域[5-7]。由于数据集的庞大,算法时间复杂度的略微提升,都会对运算时间造成严重影响。除此之外,金融学中的算法对时间异常敏感,耗费几小时或几天生成的算法可能不再实用。因此,这种特性也激发出金融学与量子计算的结合[8-10]。
本文提出了一种基于量子判别分析法(quantum linear discriminant analysis, QLDA)的投资组合优化方案,求得无目标利润下马科维茨均值方差模型[11-12]的最优解。该解在所有满足条件的投资方案中达到夏普率[13]最大。对比经典方法,可实现准指数加速。
1 马科维茨均值方差模型
投资组合优化可以描述为如下问题:投资者将一笔资金进行投资,在初期用来购买一些证券,然后在末期卖出。投资者需要在众多证券中选择哪些证券进行购买,并决定分配在这些证券上资金的份额。投资者有两个决策目标:收益率最高;风险最低。马科维茨均值方差模型[11-12]针对投资组合优化问题的建模表示为:
式中,w=(w1,w2,···wN)T,N表示可投资资产数量;wi表 示投资第i个资产的资金占总资金的份额,其解空间是连续的,因此这种模型被称为连续马科维茨均值方差模型; Σ代表收益率的协方差矩阵,大小为N×N维;E(r)为每个资产收益率的期望; µ为预先决定的收益目标。马科维茨均值方差模型的目的在于在给定收益目标后,求得一种资产配置方案使得投资风险最小。
对于不设置收益目标,只追求最大利润风险比的投资者,该模型可以转化为:
也可以转化为:
如果利率r代表资产利率减去无风险利率的净值,式(2)的目标函数被称为夏普率[13],其代表投资人每多承担一分风险,就可以多拿到几分超额报酬。夏普率是衡量一个投资方案优劣的重要指标之一。式(3)的线性形式更加普遍运用于各个优化模型中[14-16],其中 λ ∈[0, 1] 表示风险偏好,其值越大,投资策略更加偏向于考虑风险。
马科维茨均值方差模型在不同的市场或假设下也会有细微的差别。如在一个只允许做多,不允许做空的市场下,wi被约束在[0, 1]间。而在允许做空的市场下就没有这个假设。在小额投资中,wi不认为是第i个资产的资金占总资金的份额,而是购买第i个资产的手数。在这种情况下,wi是离散的,这种模型称为离散马科维茨均值方差模型。其约束条件将会调整为。在允许做空市场中wi∈{-1,0,1}, 而在不允许做空的市场中wi∈{0,1}。D为所有资产的总手数。连续型的马科维茨均值方差模型被广泛应用于实际场景,投资机构根据其结果精度,配置与精度相对应的资金规模。离散型的马科维茨均值方差模型更贴近真实情况,因为在股票市场中,投资者必须以“手”为最小单位,进行购买。离散模型可以通过增加可能离散解的个数来逼近连续模型,但算法的时间复杂度会大大提升。
求解连续马科维茨均值方差模型的经典算法包含拉格朗日乘子法[14]、混合灰色关联度法[15]、遗传算法[16]。这些算法的前提(需要)计算收益率的协方差矩阵,时间复杂度为ON2M,其中M为历史时间节点数。在求解拉格朗日乘子法时,需要计算矩阵乘积和求逆,其时间复杂度为O(N3)。因此这些算法的时间复杂至少是多项式级别的。而求解离散马科维茨均值方差模型的确定性经典算法是Brute-Force 算法,其时间复杂度为O(2N)。除此之外,GW 优化[17]算法被认为有解决离散马科维茨均值方差模型的潜力,GW 算法可以以多项式时间解决相似的最大割问题,其近似比可以达到最优解的80%[18]。即使对于马科维兹模型的延伸模型[19],求解离散问题也是一个NP 完全问题[20-21]。
解决马科维茨均值方差模型的最著名的两个量子算法是量子退火(quantum annealing, QA)[22-23]与量子近似优化算法(quantum approximation optimization algorithm, QAOA)[24-25]。这两个算法都通过解决组合优化问题来解决离散马科维茨模型。QA 利用量子的隧穿效应,进而加速优化时间[26-28]。DWave 量子退火机可以实现伊辛模型的优化。伊辛模型哈密顿函数表示为:
而将组合优化问题式(3)写为二次型形式后,可以发现该模型恰好就是伊辛模型。QAOA 将可行解编码为量子态后放入量子参数线路(quantum parameterized circuit, QPC)[29],然后利用变分量子特征值求解算法,运用经典的非线性优化器求得最优参数,最后对量子态进行测量。除这两个算法外,文献[30]基于HHL 算法,设计出复杂度为poly(log(NM))的组合优化算法[31],而文献[32]将马科维兹模型规约为二阶锥优化,然后用量子优化算法求解,其时间复杂度是O(N1.5)。
2 量子线性判别分析
2.1 线性判别分析模型
线性判别分析(linear discriminant analysis,LDA)是一种监督学习下的降维方法[33]。假设数据集是F:M×N,数据表示为 {xi∈RN: 1 ≤i≤M}。这M个数据被分在k个类中。记第c个类数据的均值为µc, 记所有数据的均值为x¯。则有类内散度矩阵SW和 类间散度矩阵SB分别为:
LDA 的目的是寻找一个N×K特征矩阵V,使得降维后的M×K数据FV类内散度矩阵足够小,类间散度矩阵足够大。因此LDA 问题变成求解优化问题:
在此将特征矩阵V转化为特征向量w分析这个问题。上述问题的对偶问题可以变为:
这是因为式(7)中w可以随意缩放,对于任意常数k满 足J(w)=J(kw)。 因此增加条件wTSWw=1后,依旧与原问题等价。该问题使用拉格朗日乘子法求解:
将上式对w求偏导后,得到KKT 条件:
对比式(7),上式等价于:
根据式(7)、式(10)和式(11)得到w就 是最大特征值所对应的特征向量。然后进行进一步转化:
问题转变为求解厄米特矩阵最大特征值所对应的特征向量:
因此,如果想求解特征矩阵V,就需要求解式(13)最大的K个特征值对应的特征向量v,然后将其转化为向量w后,拼接为V。
2.2 厄米特链积
文献[34]提出了一种方案来求解厄米特矩阵的特征向量,这种方案称为厄米特链积(hermitian chain product, HCP)。HCP 的线路如图1 所示,与HHL 算法十分相似,其目的是将f1(A1)I(f1(A1))†编码于量子密度算子内。
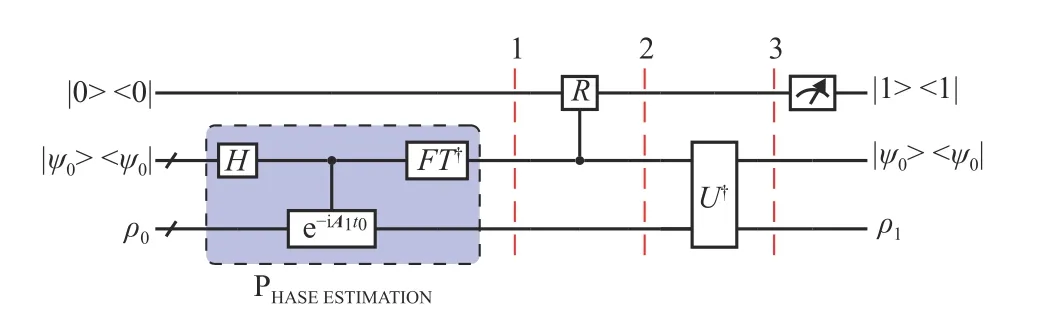
图1 HCP 线路图
量子线路的初态被储存在3 个寄存器中,第1 个储存器储存单量子比特 |0〉;第2 个寄存器可以设计任意态为初态,在理论计算上没有区别;第3个寄存器储存可变的密度算子 ρ0, ρ0在第一轮中为:
量子线路被分为3 部分,第一部分是相位估计门[35-36],其哈密顿模拟的哈密顿量就是厄米特矩阵A1。 相位估计门可以将矩阵A1的特征向量与其特征值进行纠缠。第二部分是一个控制旋转门,其旋转角度与函数f1有关,第三部分为第一部分的逆操作。最后测量第一个量子比特,如果结果为1,那么第三寄存器的密度算子则为ρ1=f1(A1)I(f1(A1))†。
如果以 ρ1作 为第三寄存器的输入,以A2和f2作为参数构造HCP 线路,那么第三寄存器的量子态表示为ρ2=f2(A2)f1(A1)I(f2(A2)f1(A1))†。这与式(13)的形式一致。
2.3 密度矩阵指数化算法
在量子判别分析[34]中,散度矩阵SW和SB通过量子随机存储器(QRAM[37-38])编码为密度算子:
式中,A和B是配平常数。而在厄米特链积中,SW和SB需 要 作 为 哈 密 顿 算 子 e-iSWt和 e-iSBt而 非 密度算子输入给相位估计门。因此,需要使用量子主成分分析(quantum principal component analysis,QPCA)[39]算法中的密度矩阵指数化算法(density matrix exponentration, DME)将密度算子转化为哈密顿量。
DME 算法的线路如图2 所示,其输入态包含n个 辅助态ρ( 被指数化的态)和一个目标态 σ(被作用于哈密顿模拟e-iρt的态)。n越大模拟精度越高。其时间复杂度为, ϵ代表误差。

图2 DME 算法线路图
整个电路由n个以交换门为哈密顿量的模拟组成,模拟时间为 Δt=t/n。S表示量子交换门。该算法基于公式:
接着利用Hadamard 引理可以得到:
因此利用交换门的哈密顿模拟可以实现密度算子的指数化。最后根据Trotter 公式[40]将上述算法递归n次后,对第一个量子比特取偏迹后为e-iρtσeiρt。因此通过复制多个密度算子,可以将其指数化。
相位估计算法使用控制下的哈密顿模拟,DME 算法也证明出,将交换门S变为控制交换门就可以实现控制哈密顿模拟的操作[39]。
3 基于QLDA 的量子投资组合优化
3.1 模型规约
首先将式(7)按照式(2)中的均值方差构造,其模型变为:
因为该模型将解w编码为量子态的概率幅,受量子计算限制,其模平方和为1。为方便书写,记R=E(r)E(r)T。 这里E(r)表 示净利率。然后将R,Σ和R1/2Σ-1R1/2谱分解得到:
式中,xi是 时间节点i时N个股票的利润向量。根据谱分解,不难看出这3 个矩阵是半正定的厄米特矩阵。使用QLDA 方法可以求解式(19)。接着将式(19)规约为式(2),并证明以下定理。
定理 如果已知式(19)的解,那么在多项式时间内可以求得式(2)的解。
在证明之前首先引入模型:
进而有如下引理。
引理1 如果有解w满足式(19),那么w或 -w其中之一满足式(21)。
证明:使用反证法进行证明,如果w或 -w都不满足式(21),那么存在w′满 足,使得下列两式之一成立:
将不等式左右取平方,有:
则w不满足式(19)条件的最大值,与原假设矛盾。
引理2 如果有解w满足式(21),那么有解u=满足式(2)。
由于目标函数的缩放性质,解乘以一个正常数时,取值不变。因此:
之后,记:
根据式(25)和式(26),式(28)满足:

3.2 基于QLDA 的投资组合优化算法
结合第2 部分内容,使用QLDA 计算投资组合问题。
1)使用QRAM 按照式(20)将矩阵R与 Σ编码为密度算子。其构造方法由文献[30]给出。
2)使用DME 算法将密度算子转化为关于R与Σ的控制哈密顿算子,以此构造HCP 线路。
3)使用HCP 算法,其链长为2,参数为f1(x)=x-1/2,A1=Σ,f2(x)=x1/2,A2=R。结 果 得到形式为R1/2Σ-1R1/2的密度算子。
4)使用DME 算法将R1/2Σ-1R1/2密度算子转化为控制哈密顿算子,并以此构造相位估计算法,并且以R1/2Σ-1R1/2作为密度算子输入。测量占比最多的量子态则对应最大特征值的特征向量v。
5)使用DME 算法将R转化为控制哈密顿算子,并构造HHL 线路,输入的函数为f1(x)=x-1/2,输入的量子态为v。 输出的量子态w满足R1/2w=v。
6)使用Swap-Test 方法[41]或经典方法计算vTE(r)≥0, 然后用经典方法计算最优配置。
资产配置的信息在这个过程中被提取在概率幅中,如何将其概率幅提取为经典信息是量子计算的解决难题。一种直观的方法是对量子态进行M次测量,然后统计每个基态的次数Mi。 那么有|vi|=。文献[30]给出一种判断vi的符号的方法,利用E(ri)的 符号来判断vi的符号,它的意义是对于正利润股票进行做多,对负利润股票进行做空。这在大多数情况是正确的,但是对于相关性比较强的股票组合,会存在误差。配置态 |v〉的其他作用包括计算风险 〈v|Σ|v〉或 者计算 〈v|v′〉来衡量其他投资策略的优劣。这两个算法无须测量都可以使用Swap-Test 方法[41]来计算。
在投资组合模型中,R只有一个非0 特征值,而 Σ也不一定满秩,也可能存在多个0 特征值。为了避免这些0 特征值带来的干扰,本算法在控制旋转门中规定一个下限κ ,小于κ 的特征值将不会引起目标比特的翻转,进而在最终测量结果为1 时,不会出现小于 κ特征值的基矢。特别地,在这种情况下,一个带有0 特征值矩阵A的逆表示为:
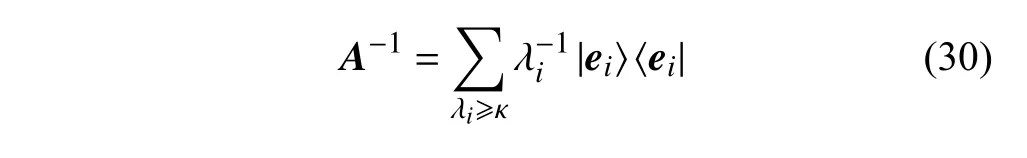
式中, λi为A的 特征值;ei为 λi的特征向量。
3.3 性能分析
基于QLDA 算法可以实现准指数加速。考虑误差项,其总时间复杂度与QLDA 一致,为O(poly(log(MN))/ϵ3)。其中将数据存储到QRAM 的时间复杂度是O(log(NM));HCP 算法不计入误差项其时间复杂度也是O(log(NM));DME 算法的时间复杂度是O(n), 因为与N无关,被认为是常数项;相位估计算法的时间复杂度是O(poly(log(MN)));HHL 算法的时间复杂度是O(log(NM));Swap-Test 算法的时间复杂度是O(log(N))。因此所有的量子算法可以实现指数加速。但在最后一步,还需要将vi求 和,这一步的复杂度是O(N)。考虑到目前应用投资组合资产种类小于100,即使将这个值扩大到 106,普通的经典计算机也可以瞬间完成,因此,这部分时间可以忽略不计。
在QRAM 中,算法需要提前将数据存储在经典RAM 中,然后使用Oracle 查询获取感兴趣的数值,这一部分的准备时间是O(NM)且是一次性的,对比其他算法也可以实现二次加速。
表1 描述了不同投资组合优化问题算法的时间复杂度。由于部分算法分析时间复杂度没有考虑误差项,因此在比较时认为误差项为常数项。数,即迭代线路的深度。从表中可见QLDA 算法与HHL 算法维持在同一水平。HHL 方法虽然没在文中特别说明,但也需要对向量上的每个元素进行求和,以满足约束条件。此表没有对消耗量子比特数目进行对比,这是因为QLDA 和HHL 需要使用Oracle 利用辅助比特构造QRAM,而二阶锥优化、QAOA、QA 需要重复算法,其消耗的量子比特难以估算。

表1 不同投资组合优化算法的对比
在制备QRAM 过程中,QLDA 与HHL 算法消耗的量子比特是一致的。在算法过程中,HHL 需要求解 3N个线性方程组,其HHL 线路需要的量子比特大致是HCP 的3 倍。因此QLDA 算法相比HHL 更加经济。
4 结 束 语
本文基于QLDA 的HCP 算法与QPCA 的DME 算法设计了无预先获利目标下的量子投资组合优化算法,算法可以求得满足最大夏普率的投资组合方案解,并且其算法的时间复杂度约为poly(log(NM)),相比于经典解决方案可以达到准指数加速。这在投资组合优化场景中,可以使投资组合优化算法所考虑的股票数量大大提高。
然而,本算法和诸多基于DME 的算法在实施时有着局限性。DME 算法需要n>100时,才有逼近指数化算子的效果。最后需要重复n次HCP 实验来获得n个R1/2Σ-1R1/2算子才可以实施相位估计算法。那么一开始在QRAM 中准备R, Σ的数量时将达到O(n2)。 尽管在理论分析中因为n与资产数量N无关,所以被认为是常数项,但在试验中这个常数值将达到1 04,是不可忽视的。如何在真实量子计算机上完成DME 算法也是挑战之一。
