碳纤维复合材料钻孔工艺与分层损伤研究

2023-12-06胡奎福徐春艳尹文潇余金桂

数字制造科学 2023年4期

胡奎福,蔡鹏,徐春艳,尹文潇,余金桂

(1.凌云科技集团有限责任公司技术中心,湖北武汉 430040;2.凌云科技集团有限责任公司复材中心,湖北武汉 430040;3.武汉理工大学机电工程学院,湖北武汉 430070)

碳纤维增强树脂基复合材料(carbon fiber reinforced polymer/plastic,CFRP)具有质量轻,比强度、比刚度高,耐腐蚀、耐疲劳性能好,可设计性强(通过改变层片的取向与顺序而改变复合材料的弹性特征和刚度特征,以满足结构的需要)等优点,广泛应用于航空航天等领域。在飞机中,复合材料构件的装配经常采用铆接和螺纹连接形式,制孔是飞机复合材料结构装配连接过程中一个必不可少的环节,而制孔质量直接影响连接结构的承载性能。虽然复合材料具有一般金属所不具备的优点,但它也存在许多弱点:脆性大(延伸率仅1%～3%)、层间强度低、抗撞击能力差[1]。因此在钻削过程中,容易出现孔的出入口纤维劈裂及孔内壁周围材料的分层[2],分层是导致工件报废的最主要原因。

Phadnis等[3]针对钻削的三维有限元仿真进行了初步研究,通过改变切削速度及进给速度,模拟了不同条件下的钻削力、扭矩、分层等,并且指出设计合理的CFRP损伤模型可以得到更为准确地仿真结果。Catalanotti等[4]通过设定CFRP的4种损伤失效模式,并建立有效的材料模型,实现了切屑形成过程中的材料损伤分析。Isbilir等[5-6]建立了CFRP的钻削仿真模型,研究了进给、转速等工艺参数与钻头几何参数对切削力和损伤的影响,并实现了对钻头结构的优化设计。Liu等[7]探索了一种尺度-跨度模型方法来模拟在钻进过程中CFRP的结构力学响应和动态渐进破坏行为。针对层间损伤,首次提出了一种基于新损伤演化规律的修正细观失效准则的动态渐进破坏理论。在建立的尺度-跨度理论模型的基础上,对CFRP的钻削行为进行了数值模拟。结果表明,所建立的尺度-跨度模拟模型与试验结果吻合较好,能够真实模拟CFRP钻进过程中预制孔的各种损伤行为。鲍永杰[8]研究了轴向力对制孔缺陷的影响,发现随着轴向力的增大,分层与撕裂程度增大;贾振元等[9]研究发现:切削深度和纤维角度影响纤维变形深度,即切深越大,纤维变形深度越大,更易产生加工损伤,随着纤维角度增加,纤维变形深度减小;Onawumi等[10]在钻削CFRP/Ti时使用超声振动作为辅助,发现超声振动可以减小切削力。近年来计算机技术飞速发展,有限元分析软件的功能日益完善,同时,CFRP价格昂贵且不易加工,因此使用有限元分析软件模拟CFRP加工的方法得到了推广。有限元分析被广泛应用于工程和学术研究中,但对CFRP加工过程中分层损伤的模拟研究较少。

笔者采用ABAQUS有限元分析软件,基于Hashin失效准则,及双线性Cohesive损伤模型中的BK(born and karman)失效准则,对CFRP层合板的分层损伤进行模拟。研究钻头转速及进给量对分层损伤的影响,为工艺参数选择提供参考。

1 试验方案

采用有限元模拟方法研究钻削工艺参数(进给量和钻头转速)对复合材料层合板分层损伤的影响,确定平面复合材料制孔过程的最优钻削工艺参数。使用硬质合金钻头在CFRP层合板上钻直径为2.5 mm的通孔,板厚为3 mm,因此设定钻头行程为3.6 mm,保证横刃可以钻出工件底层。

综合考虑现场工具配备及制孔工艺要求,在仿真中主轴转速控制在700～6 000 r/min范围内,取4个转速值(2 700 r/min,3 800 r/min,4 500 r/min,6 000 r/min);进给量控制在0.02～0.06 mm/r范围内,取3个进给量值(0.02 mm/r,0.04 mm/r,0.06 mm/r),共进行十二组试验。每一组钻孔试验完成后,提取钻削过程中稳定钻削状态下钻削力(扭矩和轴向力)的平均值和钻孔完成后的分层因子,分层因子Fd的表达式为:

Fd=Dmax/D0

(1)

式中:Dmax为孔加工后层间破坏区域最大处的孔直径;D0为所要加工的孔直径。

2 有限元仿真

2.1 钻头模型和CFRP层合板模型的建立

采用ABAQUS有限元软件建立CFRP层合板的钻削模型时,先建立CFRP层合板,圆板半径为10 mm,厚度为3 mm,层数为25层,入口层和出口层厚度为0.11 mm,其余23层厚度为0.12 mm,铺层角度如图1(c)所示。由于入口层、出口层分层损伤最严重,因此仅在在复合材料层合板上、下表面铺层处分别设置了Cohesive界面层a、b,厚度为0.01 mm。

图1 CFRP钻削模型及铺层

CFRP的失效准则采用Hashin准则,Hashin损伤模型中考虑了4种不同的损伤引发机制:纤维拉伸、纤维压缩、基体拉伸和基体压缩[11-12]。

钻削模型及铺层如图1所示。建立钻头模型时,由于钻头直径较小,且有限元仿真对钻头表面的网格质量要求较高。因此,先使用Solidworks建立钻头模型,再导入前处理软件Hypermesh中划分网格(网格密度设定为0.2),最后导入ABAQUS中,得到孤立网格的钻头模型。在进行钻头与CFRP层合板的装配时[13],钻头中心与层合板中心对齐,钻头轴线与Z轴平行,在钻头横刃与层合板间预留0.1 mm的间隙,保证钻削起始时钻头不会直接与层合板接触。

2.2 材料参数

钻头使用标准麻花钻,麻花钻的几何参数如下:钻头直径D=2.5 mm,螺旋角β=30°,横刃斜角Ψ=50°,顶角2φ=120°;麻花钻的力学性能参数包括杨氏模量E=210 000 MPa,泊松比μ=0.25,密度ρ=8.3×10-9t/mm3。CFRP层合板的力学性能参数如表1所示,设定Cohesive界面单元的损伤稳定粘性系数为0.000 01。

表1 CFRP层合板力学性能参数

2.3 边界条件和网格划分

CFRP层合板利用扫略网格的方法进行离散化,单元类型为八节点减缩积分连续壳单元(SC8R)。Cohesive界面层采用为边布种的方式进行离散化,单元类型为三维八节点粘性单元(COH3D8)[14],在设置Cohesive层时将最大刚度退化系数设定为0.98,以增加计算收敛性。当材料刚度下降率SDEG值达到0.98时,表明Cohesive单元已经失效,失效单元被删除后形成分层损伤。

对中心半径为3 mm的区域使用边布种的方式进行网格细化,CFRP层合板模型的边界条件为外周固定。钻头采用自由网格划分方式,将麻花钻设为刚体,单元类型设定为三维四节点四面体单元(C3D4)。沿钻头钻进方向设置钻头的角速度和进给速度,同时限制其他两个方向的位移和转动。

3 结果分析

3.1 钻削过程应力分析

图2为CFRP层合板钻削过程仿真不同阶段的示意图。CFRP层合板的钻削加工过程大致可分为3个阶段。

图2 CFRP层合板钻削过程中Mises应力变化

阶段I为初始阶段,即钻头横刃接触层合板到主切削刃完全钻入层合板的过程;图2(a)中钻头横刃刚钻入层合板时,属于Ⅰ阶段。阶段Ⅰ中主切削刃首先使钻入口处纤维层剥开,然后把它切断,这种剥离是产生分层的重要原因,该阶段中切削面积不断增大,轴向力增长较快。

阶段II为主切削刃完全进入层合板内切削的过程,副切削刃开始切削孔壁材料;图2(b)中钻头主切削刃已完全进入层合板,属于阶段Ⅱ。阶段Ⅱ切削面积不变,轴向力数值上下波动,变化不大,该过程中待切削材料层不断减少,材料刚度降低。

阶段III为钻头横刃到达层合板底部层至主切削刃完全钻出的过程;图2(c)中横刃已钻出层合板底层,图2(d)中钻头主切削刃已完全钻穿层合板。当钻头横刃接触到最底层纤维时,给了底层纤维一个向外推的力,使得钻出口处纤维层与基体分离,导致钻出口处纤维层出现分层、撕裂等缺陷。随着横刃和主切削刃逐渐钻出层合板,切削面积减小,轴向力逐渐减小,直到钻头完全钻穿层合板,轴向力慢慢趋于零。

3.2 钻削工艺参数对分层损伤的影响

如图3和图4所示,钻头开始钻入后轴向力和扭矩均由零逐渐增大,其中轴向力增大的幅度快一些;当钻头主切削刃全部钻入层合板时轴向力和扭矩达到最大值,在钻头未钻出前一直保持这一稳定状态。钻头钻出过程开始后轴向力和扭矩均开始下降,直到钻头完全钻出变成零,其中扭矩的下降较轴向力的下降要滞后。钻削过程中轴向力和扭矩都有一定的波动,其中扭矩的波动量更大,且波动频率更快。

图3 不同钻削工艺参数下扭矩随钻削深度的变化

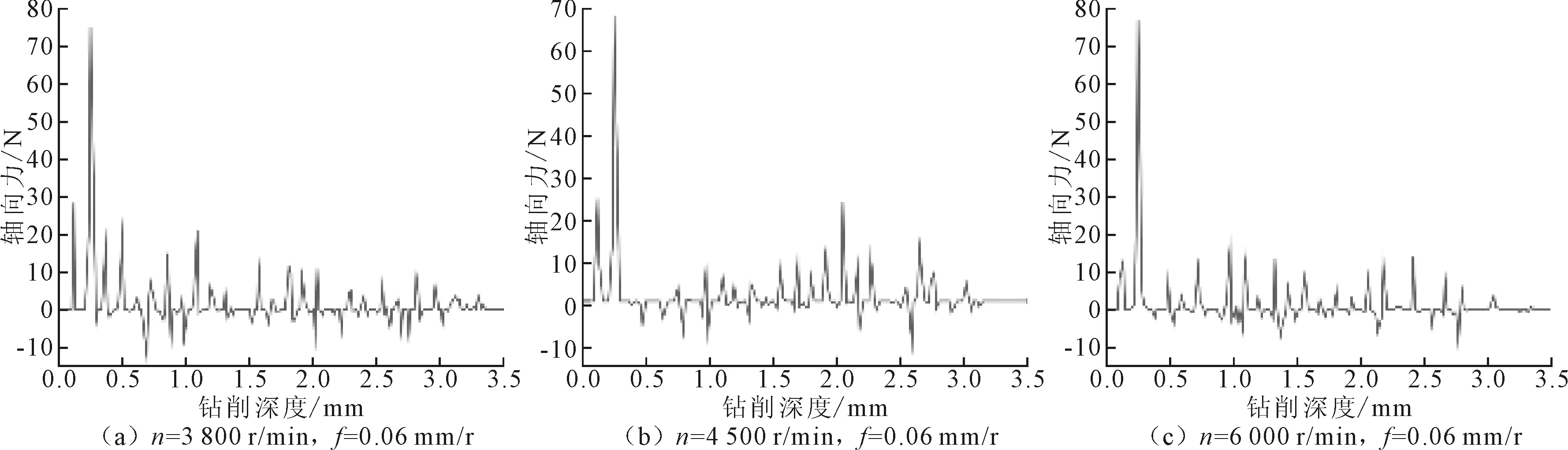
图4 不同钻削工艺参数下轴向力随钻削深度的变化

图5为钻孔后上表面、下表面铺层界面损伤结果。分层损伤集中在孔周,复合材料层合板在下表面铺层界面处的分层损伤较上表面铺层界面处的损伤更为严重,因此提取下表面铺层界面处的分层因子作为参考。

图5 不同钻削工艺参数下钻孔后上、下表面铺层界面损伤结果

不同钻头转速条件下复合材料层合板钻削过程中平均扭矩、平均轴向力与进给量的关系如图6所示。从图6可知,控制转速不变时,进给量越大,平均扭矩、平均轴向力越大;这是因为随着钻头进给量的增大,切削刃单位时间切削的材料增加,故钻头受到的摩擦力因而增大,导致轴向力有增大的趋势,分层因子随之增大。控制进给量不变时,转速越大,平均扭矩、平均轴向力越大。这是由于随着转速的增大,切削速度和进给速度增大,单位时间材料去除量增加,导致轴向力和扭矩增大,分层因子随之增大。