基于操作分析 注重量感培养
2023-12-06邵爱珠董燕菲
文|邵爱珠 董燕菲
一、习题展评
●习题一
1.习题内容
选择合适的方法画角:分别画一个50°和135°的角,并说说你选择什么工具画角()
A.直尺 B.量角器
C.三角尺 D.圆规
2.能力指向
考查学生对一般的画角方法的掌握情况,能正确运用量角器画指定度数的角,另一方面也考查了学生对三角尺上各个角的认识,以及用特殊角进行灵活拼组的能力,发展学生的空间想象能力。
3.学情分析
对城乡结合部某校四年级88名学生进行了测试。统计结果如下表:

角的大小画图工具正确人数画50°的角画135°的角画图人数画图人数正确人数量角器88886969三角尺001919
测评数据显示,100%的学生选择用量角器画50°的角,正确率100%。78.41%的学生选择用量角器画135°的角,正确率100%。说明学生用量角器画角的基本技能掌握扎实,另有21.59%的学生选择用三角尺画135°的角,正确率100%,这些学生能发现135°是一个由90°角与45°角合并而成的特殊角,可以借助三角尺进行组合画角。
学生作品如图1:

图1
●习题二
1.习题内容
你能读出下面各角的度数吗?试一试。
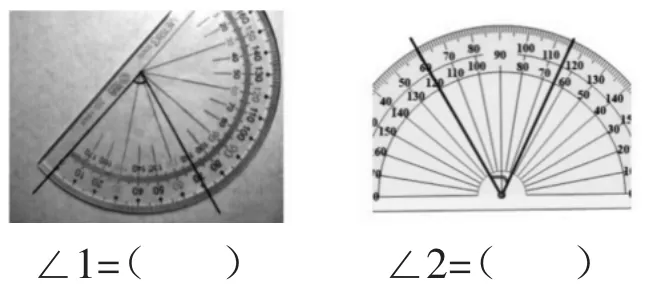
2.能力指向
考查学生在量角器上正确读出角的度数的能力。图中两个角没有一条边在水平位置上,这对学生来说度量是有困难的,尽管度量∠2 的量角器是标准的水平位置摆放,但并不是从0 刻度线开始度量,这些因素都给学生正确读出角的度数设置了障碍。通过检测,考查学生能否真正掌握角的度量本质,发展学生的量感。
3.学情分析
通过检测发现:当角的一边与0 刻度线重合时,100%的学生能正确读出角的大小;当角的两边都没有与0 刻度重合时,81.82%的学生能正确读出角的大小。通过访谈了解到,学生将之前用断尺测量物体长度的经验,巧妙迁移到∠2 的度量,有的通过10°、10°地数,得到∠2 的度数,还有的用“最终刻度减起始刻度”的方法,算出∠2 的度数。由此发现学生对于读量角器上度数掌握得比较扎实。
当角的两边在任意刻度时,有近五分之一的学生读取数据存在一定的困难,有部分学生根据角的边所对的刻度,直接错读成60°、65°、115°、120°等,他们仅仅把一般的量角方法进行了迁移,同时也反映出这部分学生对锐角、钝角的表象没有充分建立,从而没有真正理解度量本质。
●习题三
1.习题内容

2.能力指向
考查学生灵活测量角的能力,借助工具度量与计算角的大小相结合,进一步发展学生的量感和推理能力。
3.学情分析
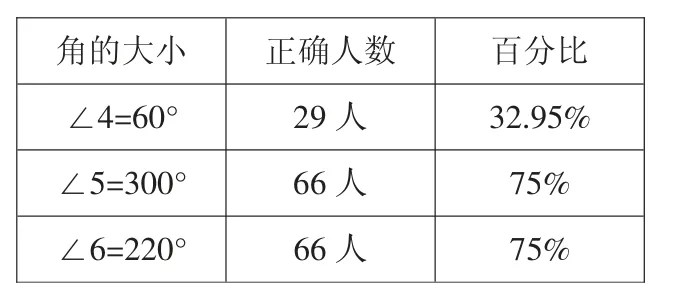
角的大小正确人数百分比∠4=60°29 人32.95%∠5=300°66 人75%∠6=220°66 人75%
测评数据显示,学生用量角器量60°角时,度量的正确率仅32.95%,远远低于画角和读数的正确率,有55 位学生的度量结果是63°、65°,存在3°~5°的误差,还有4 位学生测量结果是115°、120°等,这一结果引起了我们的好奇:∠4 是一个标准的锐角,且一条边在水平位置上,为什么学生无法准确测量呢?通过访谈发现,存在两方面原因:原因一,如图2-1 技能方面,当角的两边所画长短不同时,学生没有将边延长,只是通过粗略的估计得到结果;原因二,如图2-2 概念方面,学生对角的认识与理解不够到位,在用量角器度量时,只关注对应边与刻度重合的位置,而忽略了角的大小。
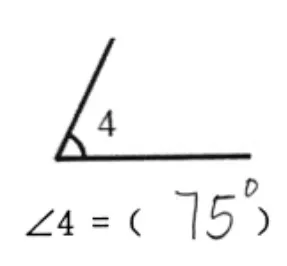
图2-1
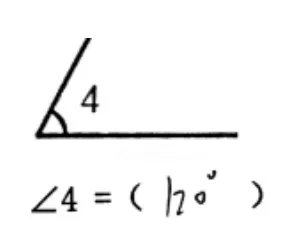
图2-2
对∠6 度量结果做了专项分析,根据学生解答的具体表现,划分为五个水平层次:

水平层次具体表现水平0无从下手或直接空着。测量∠6 对应的劣角,结果小于90°。水平1images/BZ_34_1126_1488_1391_1667.png测量∠6 对应的劣角,结果大于90°。水平2images/BZ_34_1127_1803_1415_1990.png将∠6 分割成“平角+锐角”,分别测量再相加,结果正确。水平3images/BZ_34_1033_2123_1512_2334.png用“周角-钝角”的方法测量∠6,结果正确。水平4images/BZ_34_1030_2537_1512_2774.png水平层次人数百分比水平033.41%水平133.41%水平21314.77%水平31314.77%水平45663.64%
数据显示,水平0、1、2 的学生占了21.6%,说明这些学生对∠6 的大小无法正确识别,还有个别学生对钝角、锐角的表象认识不清晰,致使无法解决问题;75%左右的学生能得到正确结果,其中15%左右的学生能基于已有知识,将优角分割,转化成一个平角与一个锐角之和,通过分别测量再相加的方法,得到∠6 的度数,有64%左右的学生用周角减对应的劣角,得到∠6 的度数。通过访谈了解到,这些学生都发现了∠6是一个比平角大、比周角小的角,用量角器无法直接测量∠6,于是将未知的∠6 转化成已知的角的和(差),从而解决问题,具有较强的量感以及一定的推理意识。
二、教学建议
1.动静结合,完善角的认识
关于“角”的定义有两种不同的方式:一是静态描述,也就是教材中呈现的“从一点引出两条射线所组成的平面图形叫作角”;二是动态描述,即“一条射线绕着它的端点从一个位置旋转到另一个位置所形成的平面图形叫作角”。教学时可以借助活动角,固定其中一边,然后缓缓旋转另一边,使学生清晰观察到角产生以及变化的过程,观察到角的始边与终边。通过化静为动的教学呈现,丰富对角的感知,加深对角表象的理解。
2.先估后量,增强空间观念
先估后量是解决一部分学生将量角器内外刻度圈混淆的问题而采用的比较好的方法。用量角器量角前,先根据角的大小估计度数。学生最熟悉的是以直角为参照对象,估出大于90°或小于90°,再根据一些特殊角的大小,估出度数。接着再用量角器量,同时再次验证估的是否接近。这样先估后量不但培养了学生的量感,同时也更有利于形成角的大小的表象,增强空间观念。
3.加强沟通,感悟度量本质
学生在学习角的度量之前,已有一定的度量经验,已经储备了用直尺测量线段的长度、用单位面积测量物体表面的经验。角的度量虽然与长度、面积等有着明显的不同,但其度量本质是相同的,都是用测量单位去度量的过程。因此在学生掌握基本的角的度量方法基础上,要注重变式练习,呈现非标准化测量练习,以打破思维定势,感悟度量本质,提升学生思维能力,为后续学习奠基。
