基于连接关系动态的复杂网络外同步控制

陈金彪, 王银河*, 汤 晓

(1.广东工业大学 自动化学院, 广东 广州 510006; 2.广州亚俊氏真空科技股份有限公司, 广东 广州 510006)

0 引言

一个复杂动态网络通常是由相当多数量的动态节点相互连接构成,这种节点间错综复杂的连接关系组成了网络的拓扑结构.近些年来,关于复杂动态网络的拓扑结构和节点动态行为的研究受到众多学者的关注.尤其是针对复杂动态网络同步问题的探讨已经成为网络科学研究领域内的研究热点.

复杂动态网络同步主要分为内同步和外同步.内同步[1-9]是将网络中的每一个节点看作为动态系统,在同一个网络中呈现出节点状态趋同的集体动态行为,例如多锤桩振动系统(网络)中的振动桩锤(节点)之间相位和速度同步[9].外同步则关注不同网络之间对应节点间状态的趋同行为,而不关注一个网络内的节点动态行为,例如卫星网络(驱动网络)和地面网络(响应网络)之间的频率同步[10].

在复杂动态网络外同步的研究中,网络的拓扑结构是其中一个重要议题.在利用代数图论方式对复杂动态网络进行建模时,可以利用实数作为加权值来量化节点间的连接强度,由此形成了加权复杂动态网络,其拓扑结构可以用其实数加权值构成的连接关系矩阵定量描述.目前针对具有定常连接关系矩阵的复杂动态网络(连接关系是时不变的)的外同步已有许多研究成果[11-13],随研究的深入,有关时变拓扑的网络外同步取得许多成果[14,15].

值得注意的是,某些现实网络的拓扑结构变化还有可能受到节点的状态变化影响.例如在工业卷绕系统中,平带的张力(连接关系)因电机的转速(节点的状态)的变化而变化[16,17]; 神经网络中神经元的突触(连接关系)因神经元(节点)发生Gamma震荡产生易化[18].所以,连接关系的变化与节点的状态有关,因而可以视为节点状态变量的函数,将所有的连接关系在整体上视为一个系统,并利用其辅助实现外同步.

受上述讨论的启发,本文在研究网络外同步时,认为每一个复杂动态网络都可以看作是由节点子系统和连接关系子系统耦合而成的组合系统,借助连接关系子系统来辅助节点子系统实现网络外同步,其中连接关系的加权值可以视为连接关系子系统的状态变量,因而网络连接关系矩阵可视为连接关系子系统的状态矩阵,其变化不仅是时变的而且也受节点状态变化的影响.特别地,当连接关系子系统辅助网络节点子系统实现外同步后,此时的网络拓扑结构也会呈现出某种特定的形式,不同形式的网络拓扑对应于不同的网络背景要求.换句话说,在连接关系辅助节点实现外同步的同时,使网络自身的拓扑结构呈现出事先指定的形式具有非常重要的现实意义.例如,星型结构常用于计算机网络中,能使网络内的设备便于集中管理和故障诊断[19];小世界特性的网络结构有较高的聚合性和较短的平均路径长度[20].研究发现,大脑结构和功能网络具有小世界特性,有更快的信息传递速度,更强的计算能力[21].所以,在进行网络外同步控制时,针对网络的需求选择合适的拓扑结构有助于提升网络整体性能.

综合上述考虑,本文研究下面的网络外同步问题:考虑两个网络(驱动和响应网络),在驱动网络的动态连接关系未知的情况下,为响应网络设计合适的节点控制器和网络动态连接关系,使驱动和响应网络对应节点间的状态实现外同步,同时,响应网络的最终拓扑结构能按照事先指定的方式呈现.

上列问题的实质是利用响应网络的动态连接关系辅助实现驱动响应网络之间的外同步,并且保证响应网络的最终拓扑能够按照事先指定的方式呈现,这类问题在现有的文献中鲜有讨论.针对这类问题,文献[22,23]研究了网络外同步控制问题,但不涉及网络拓扑布局分析;文献[24]实现了一类网络结构平衡控制,但不关注节点状态同步;文献[25]不仅实现了网络外同步,而且响应网络拓扑呈现位驱动网络拓扑表现形式,但响应网络的拓扑表现并不是独立的,需按照特定的形式呈现,并且与驱动网络拓扑有关.由此可以看出,针对上列问题的完全解决方案鲜见于报道.

基于以上讨论,与以往文献相比,本文主要有两点优势:(1) 在对复杂动态网络的认识上,本文将网络的所有连接关系在整体上视为一个动态子系统(另一个是节点子系统),利用响应网络的连接关系子系统辅助两个网络之间对应节点的状态实现外同步;(2) 在控制策略合成方面,在驱动网络的时变动态连接关系未知有界的情况下,为响应网络的节点子系统设计自适应控制器,为连接关系子系统设计动态耦合结构,以此不仅能够保证实现网络外同步,而且能够使响应网络的最终拓扑按照事先指定的方式呈现.

1 模型描述和基本假设

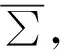
(1)

(2)

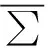
注1通过驱动响应网络模型中,可以看出本文提出的网络模型由非线性项和耦合项组成,其中的耦合项中不仅含有网络内部节点的耦合,还存在网络间节点的耦合,这种形式体现出了复杂网络的复杂性.

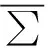
(3)

(4)

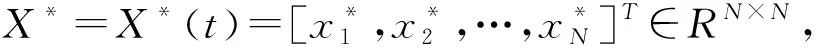
假设1引入的外部辅助矩阵信号X*是有界的,且状态可测.

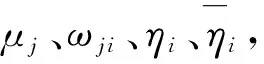
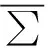
若假设2成立,容易验证下列不等式成立:

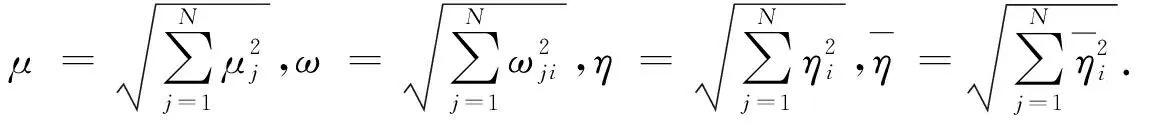
2 外同步控制设计

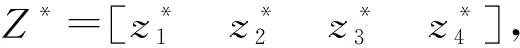
(5)

式(5)中:λ1是正的可调参数,P1和P2为待设计项.

自适应律和响应网络连接关系更新律如下:

(6)

(7)

式(6)、(7)中:λ2、ρ是正的可调参数.

由E=Z-Y和方程(3)、(4),得误差系统方程:

(8)

将节点自适应控制器(5)代入式(8)可得误差闭环系统动态方程:

(9)

考虑如下正定函数:

(10)

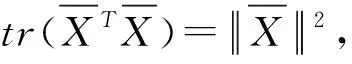
(11)

(12)

由自适应率(6)、连接关系更新率(7)和不等式(12)得

(13)

(14)

不等式(13)可以被重写成以下形式:

(15)

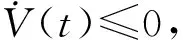
(16)

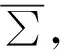
注5定理1的使用步骤如下:

step1 考虑驱动网络∑的节点系统(1),验证非线性函数fi(yi,t)、耦合函数hj(y,t)以及连接关系lji(y,z,t)是否有界,否则定理1失效.

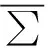
step3 确定外部辅助矩阵信号X*,判断是否状态可测且有界.

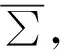
3 数值仿真

选择连接关系矩阵:

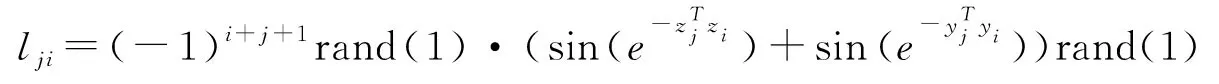
选择连续非线性向量函数:

选择WS小世界网络模型作为外部辅助矩阵信号,其中N=50,K=6,P=0.3.

注6WS小世界网络模型生成步骤如下:

step1 选一个具有N个节点的环状最近邻耦合网络,每个节点都与它左右相邻的各K/2个节点相连,K是偶数.

step2 把网络每条边保持一个端点不变按概率P重连除自身外的另一个端点,其中不可重连.

由上述步骤生成的小世界模型如图1所示.

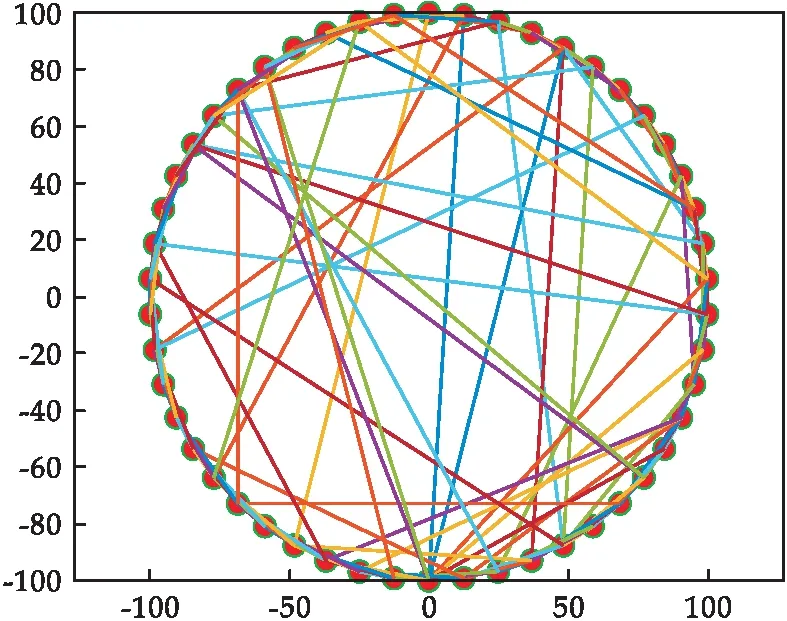
图1 小世界模型

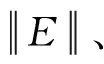
图2 误差范数的响应曲线

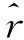
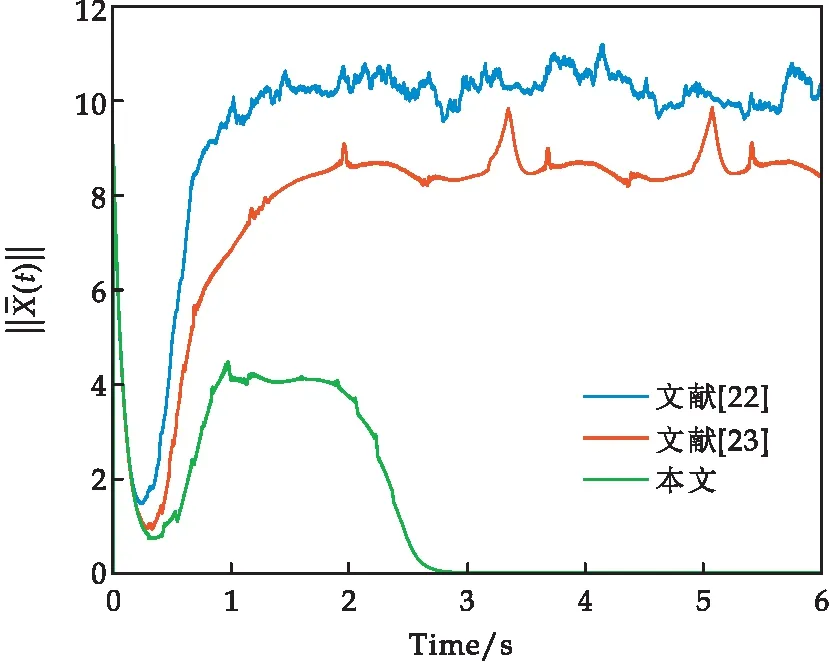
图3 连接关系误差范数的响应曲线

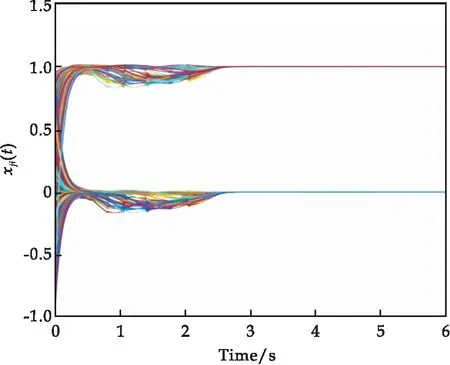
图4 本文连接关系xji的状态响应曲线

图5 本文参数估计量的响应曲线

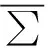
4 结论

本文针对一类节点动态和拓扑结构相互耦合的复杂网络外同步问题,通过给定的外部辅助矩阵信号,并基于节点动力学和lyapunov稳定性理论为响应网络构造动态连接关系和自适应控制器,实现驱动网络与响应网络间的外同步.结果表明响应网络的拓扑结构能够按照预先设定形式呈现,同时实现网络外同步,最后通过数值仿真验证了本文的有效性.但是本文仅考虑耦合无时滞以及网络节点内连的情况,但实际工程中时滞系统和网络间的互联情况也是广泛存在的.因此,本课题组后续的研究工作将会围绕以上问题展开探讨.