基于响应面分析法的多通道烘缸换热性能分析与参数优化
2023-12-06董继先郭浩增乔丽洁
董继先, 郭浩增, 王 莎, 乔丽洁, 王 博, 刘 欢
(1.陕西科技大学 机电工程学院, 陕西 西安 710021; 2.西安航空职业技术学院 自动化工程学院, 陕西 西安 710089; 3.陕西科技大学 材料科学与工程学院, 陕西 西安 710021)
0 引言
烘缸是造纸工业中重要的设备之一,对于提高烘缸的换热效率这一问题,提升烘缸内部的冷凝水排放是一个重要的解决方案,为此,多通道烘缸这一烘缸结构被提出[1],并于后续的研究中进行了优化[2,3],具体结构如图1所示,其目的在于利用蒸汽压力排出烘缸内部的大部分冷凝水,并在后续的研究中,多通道烘缸在换热性能提升的优势得到了证实[4].

图1 多通道烘缸结构示意图
对于多通道烘缸的研究方面,由于烘缸实际工作的状态为绕水平轴线转动,研究难度相对较大,因此部分学者首先基于静止状态下烘缸进行了实验研究.Yan Y等[5]对静止状态下多通道烘缸矩形水平流道的流形进行了研究,得出在未转动的条件下,低质量流速出现塞状流、波状流等流形,而高质量流速下则是环状流和波状流为主而没有出现塞状流,其流型与已有的流型图基本一致,并得出了与实验吻合较好的已有的换热和压降关联式;随后又对不同的通道结构参数对烘缸换热特性的影响进行了研究[6],得出多通道烘缸的建议通道数量为150~200,横截面长宽比为1∶3,间距比为1∶1~1∶3时,烘缸的整体换热性能最佳.乔丽洁等[7,8]则对静止状态下多通道烘缸流道冷却参数对换热性能的影响进行了研究,得出蒸汽质量流速增大或用于模拟湿纸幅的冷却水质量流量增大时,烘缸的整体的换热系数都会提升,但随着冷却水质量流量的增大,换热系数出现了波动,因此增大蒸汽质量流速是实现换热效果提升的较好方案;后续又对通道内的压降情况分别用分相流和均相流模型予以研究[9],结果表明均相流模型不适用于通道内压降的计算,并筛选出了相对较好的压降契合模型;并对U型截面通道的流型分布情况和流动特性进行了研究[10],得出环状流出现的最佳正其质量流量与冷却水质量流量分别为35 kg/(m2·s)和198 kg/h.董岩等[11,12]对于不同的截面形状对换热性能的影响也进行了研究,得出了换热面积相同的情况下,U型截面的流道换热效果优于其他截面形状的流道.
基于静止状态多通道烘缸研究,王莎等[13,14]设计了多通道烘缸的旋转实验台,并进行了应力分析和模态数值分析,确保了实验台的机械安全性,随后又以该实验台为基础,对旋转状态下多通道烘缸的换热性能与压降的研究[15,16],得出换热系数随雷诺数、旋转雷诺数与入口蒸汽温度的变化规律,以及压降随蒸汽质量流速,旋转雷诺数的变化规律,并对旋转状态下的换热系数和压降给出了新的拟合公式,有较好的吻合度.张树林等[17]对旋转状态下,冷却水侧的参数变化对烘缸换热性能及压降的影响进行了研究,指出通道平均换热系数随冷却水质量流量的增大而增大,压降则随之减小并稳定于以定值.
由上可见,对于多通道烘缸换热性能方面的研究已经较为成熟且丰富,对于烘缸换热系数与各参数间的关系进行了深入研究并得出了适合的关系式,但所得关系式往往参考变量多,形式复杂,难以以直观地方式明确得到换热系数随各参数的变化趋势,从而难以对烘缸换热性能进行可行的优化操作.
响应面分析法是通过设计合理的有限次数试验,建立一个包括各显著因素的一次项、平方项和任何两个因素之间的一级交互作用项的数学模型,精确研究各因素与响应值之间的关系,快速有效地确定多因素系统的最佳条件.相比基于相似性原理的无量纲关系式,响应面分析法得出的多元二次多项式形式更为简洁,可以更直接的把握各自变量与因变量的函数关系,更容易进行优化处理.为探究烘缸换热性能的优化方向与具体的优化参数,本文选取转速和蒸汽质量流速为代表变量,利用响应面分析法,对烘缸的换热性能与二变量间的关系进行研究,并得出具体的参数优化区间.
1 实验原理
实验针对多通道烘缸中发生冷凝换热的两相部分进行研究.考虑到烘缸尺寸等参数的差异,要对换热系数、蒸汽质量流速和转速三个参量进行无量纲处理,同时考虑实验过程中可能出现的热损失,以保证结果的准确性和可推广性.
(1)无量纲换热系数,采用对流换热常用的努塞尔数Nu为代表:
(1)
式(1)中:Dh为蒸汽侧通道的水力直径,m;λH为蒸汽侧流体两相热导率,W·m-1·K-1:
(2)
式(2)中:λg,λl分别为当前温度下饱和汽与饱和水的热导率,W·m-1·K-1;x为当前流体的干度,即质量含汽率,其计算方法如下:
(3)
式(3)中:h′与h″分别为当前蒸汽侧温度下的饱和水比焓与饱和气比焓,kJ·kg-1,均根据当前蒸汽侧流体温度查表获得[18];h为当前蒸汽侧流体的比焓,kJ·kg-1,由于流道中各位置的比焓根据能量守恒定律,因此可通过计算冷却水侧的吸热量对其进行计算:
(4)
式(4)中:hi+1为目标位置的流体比焓,kJ·kg-1;hi为目标上一位置的比焓,kJ·kg-1;cp为冷却水的定压比热容,kJ·kg-1·K-1;qm,c为冷却水的质量流量,kg·s-1;Tc,i+1和Tc,i则是对应的冷却水温度,K.
式(1)中:hs为蒸汽侧对流换热系数,W·m-2·K-1,具体计算方式由牛顿对流换热公式获得:
(5)
式(5)中:As为换热面积,m2;Ts为当前蒸汽侧温度,K;Tw为对应的换热壁面温度,K;Q为换热热量,kJ;根据能量守恒定律,在热损失较小可忽略不计的情况下,蒸汽侧放热热量等于冷却水侧吸热量,即:
Qi=cpqm,c(Tc,i+1-Tc,i)
(6)
(2)无量纲流速,以流道中的气相雷诺数Reg为代表:
(7)
式(6)中:G为流道内流体的质量流速,kg·m-2·s-1,为当前通道内流体质量流量qm,s,kg·s-1,与流道横截面积A,m2,的比值:
(8)
式(8)中:μg、μl为流道内流体的气相动力粘度(Pa·s),其具体值为当前温度下的饱和水蒸气动力粘度,由当前蒸汽侧温度查表获得.
(3)无量纲转速,以旋转雷诺数Reω为代表,该无量纲参数由Morris提出并用于旋转状态下的换热系数关系式计算[19,20],其计算公式如下:
(9)
式(9)中:ω为流道旋转的角速度,rad·s-1;νH为流道的两相运动粘度,m2·s-1,其计算公式如下:
(10)
式(10)中:νg和νl分别为当前温度下饱和蒸汽与饱和水的运动粘度,m2·s-1,可根据当前蒸汽侧温度查表获得.
(4)热损失方面,考虑到热损失过程接近于管外强迫对流换热,因此基于管外强迫对流换热公式[21]即可计算热损失,具体公式如式(11)所示:
(11)
式(11)中:Nuloss为强迫对流换热的努塞尔数;ha为热损失的对流换热系数,W·m-2·K-1;L为流道长度,m;λa为空气热导率,W·m-1·K-1;Rea和Pra分别为空气的雷诺数与普朗特数,可以根据转速和当前室温温进行查表.
2 实验设计
根据理论部分,需要测量的物理量包括蒸汽侧流体、冷却水和换热壁面的温度、蒸汽侧质量流量,同时设定实验台转速.具体设计的实验台的结构如图2所示.
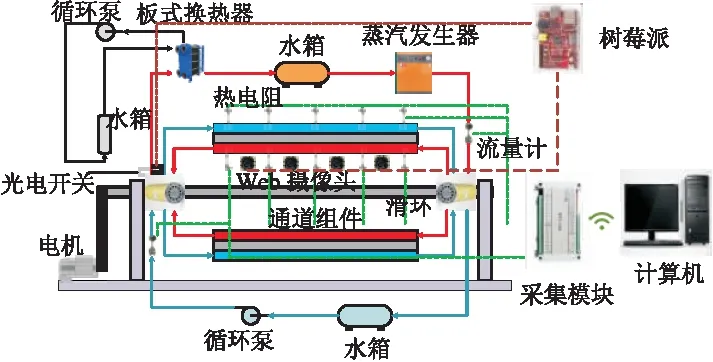
图2 实验台结构示意图
实验台由机械系统、流体循环系统和传感器系统三大部分组成,机械系统包括最基础的支撑结构部分旋转电机,其中电机的转速由相连的变频器进行控制,并经过折算得到对应的转动角速度.
流体循环系统包括蒸汽发生器、连接管路、分布滑环、流道板、换热器、循环水泵、储水箱、滤水系统等部分组成.蒸汽由蒸汽发生器产生,冷却水由冷却水泵泵出,经管道分别送至实验台两侧的分布滑环,分布滑环保证实验台在转动情况下,蒸汽和冷却水可以顺利被送入送出流道板,蒸汽和冷却水在流道板中进行热交换后,由分别由各自对侧的滑环流出,送入换热器进行冷却,蒸汽侧冷凝水经过滤后流入发生器水箱,冷却水侧冷水则进入冷却水箱,分别进入下一次的循环.流道板除了正反两侧的蒸汽/冷却水流道外,流道周围有凹槽安装隔热的密封条,如图3所示;同时整个流道板和蒸汽侧进口段管路均有厚度在1~3 cm的隔热棉包裹,最大限度的减少热损失.经计算,实验台的热损失小于2%,可以忽略不计.最终搭建完毕的实验台如图4所示.

图3 流道板结构示意图

图4 实验台实物图
本实验所用传感器系统是采集各种参数数据的部分,主要包括PT100热电阻、流量计、信号采集卡三部分,热电阻的排布如图5所示,分布于整个流道板上,共分为三组,分别测量蒸汽侧流体、冷却水侧流体和两侧中间的换热壁面的温度.蒸汽侧和冷却水侧的流道入口均设有流量计测量两回路的流量.热电阻的信号则由采集卡采集,并通过Wi-Fi传输至计算机.

图5 热电阻排布示意图
本实验台所使用的传感器精度如表1所示,实验台的结构尺寸参数如表2所示,实验的具体参数如表3所示.具体的实验步骤如下:

表1 传感器精度表

表2 实验台结构参数

表3 实验参数表
(1)接通所有用电设备电源,蒸汽发生器预热,连接所有无线传输模块,测试各传感器读数是否正常.
(2)打开所有管路,调整冷却水流量;调整蒸汽发生器温度至设定值,微调流量控制阀至蒸汽质量流量达到实验所需大小.
(3)启动电机,通过变频器控制当前转速,待传感器读数基本稳定后开始采集数据.
(4)数据采集完成后,调整电机转速或蒸汽流量,继续下一组数据的采集,直至所有实验组数据采集完毕.
(5)断开所有用电器电路,确认电源总闸关闭;蒸汽发生器带压排污,关闭进水口,排空进水水箱;保持冷却水持续供应至实验台完全冷却,关闭所有管路.
(6)所采集的数据经Excel预处理后,交予Python做进一步处理,绘图,得出所需方程.
3 实验结果与优化分析
3.1 实验结果
实验结果以Reg和Reω为坐标的三维散点图展示如图6所示.由图6可知,提高蒸汽质量流速对换热性能有整体上的提升,而在两较高的质量流速下,随着转速增大,换热性能亦随之提升,但在流速较低时,Nu基本只随Reω变化而出现小幅波动,而没有大的明显变化,可见流速较低时,转速对换热性能的影响是相对有限的.由于本实验只针对出现冷凝换热的部分进行研究分析,没有冷段的温度数据参与计算,因此本实验所得的Nu整体上要大于文献[15]中所得的结果,但所得变化规律基本与文献[15]中所描述的一致.
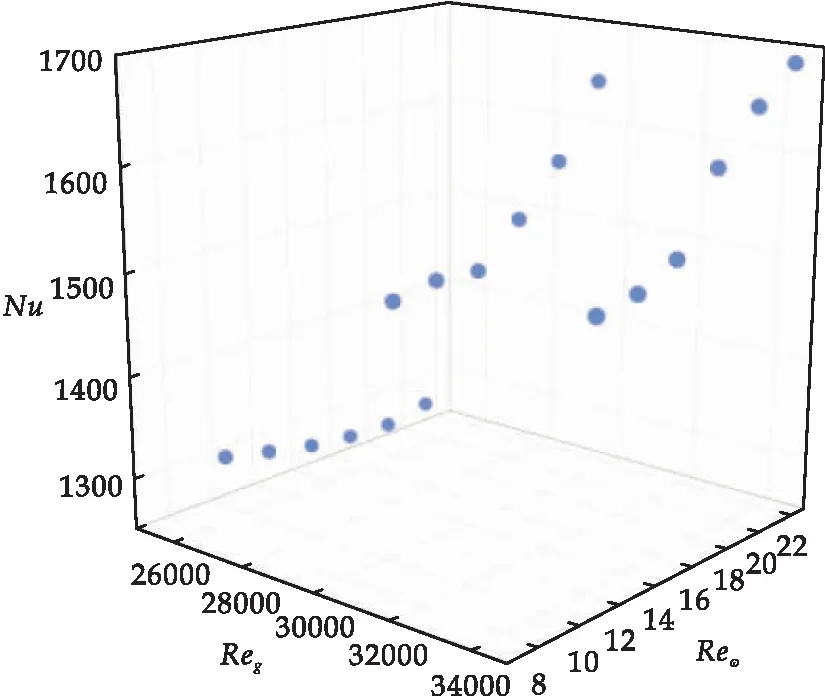
图6 Nu随Reg和Reω变化的三维分布图
图6较好地表现了实验所得的换热性能的变化情况,但要总结换热性能随转速和蒸汽质量流速的变化规律,优化对还需要对数据进行进一步的处理与分析.
3.2 响应面的构建
图6展示的实验结果表明,因变量Nu与自变量Reg和Reω并非二维线性关系,因此构建响应面的拟合函数采用二次多项式,如公式(12)所示:
(12)
式(12)中:bi为拟合系数,ε为误差.视所有一次项和二次项均为不同的一次自变量,则可将该二元二次多项式化为多元线性多项式:
(13)
式(13)中:xi为公式12中对应的各一次项与二次项变量.由于Reg与Reω以及相关二次项变量的数量级相差过大,因此为保证结果的精度,降低拟合误差,对各自变量采用标准化处理,即:
(14)
式(14)中:μi、σi分别为xi训练值的均值与标准差.最终线性回归方程为:
(15)

表4 回归方程的方差分析

表5 回归系数的估计值与标准误
由此可列出回归方程为:
(16)
或:
(17)

图7 对Reg和Reω的响应面
3.3 基于响应面的优化分析
为了对Reg和Reω进行优化分析,令式(17)分别对Reg和Reω取一阶偏导,可以得到:
(18)
令式(18)两式分别等于零并联立求解,我们可以得到驻点,但函数在驻点处的Hessian矩阵为不定矩阵,因此该驻点为鞍点而非极值点,方程在该区间内最大值即为Reg和Reω均取最大时的值.由此可见,在当前实验区间内,保证尽可能高的质量流速和转速是获得高换热性能的必要条件.
Reg*=237.09Reω,c+2.93×104
(19)
(20)
式(19)、(20)中:Reg*与Reω*分别表示两变量的最优值;Reg,c与Reω,c分别表示两变量取区间内定值.
3.3.1 定Reω下的参数优化分析


图8 Reg*关于Reω的函数图像

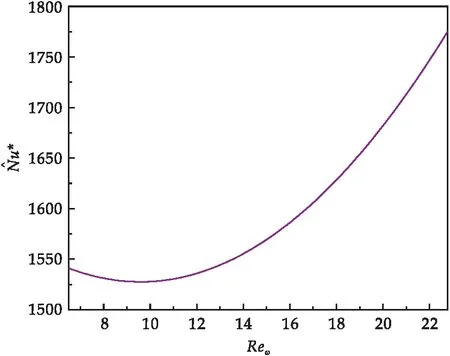
图9 关于Reω的函数图像
3.3.2 定Reg下的参数优化分析


图10 不同Reω*条件下关于Reg函数图像

(21)
3.3.3 当前区间的综合优化分析


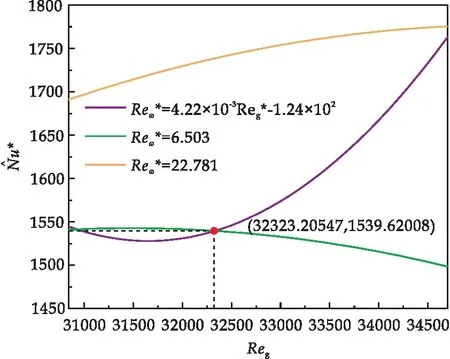
图11 不同优化方案的对比
根据以上分析,可以得出当前区间内多通道烘缸换热系数的最终的优化结果.当转速一定而蒸汽质量流速可调时,质量流速应至少保证气相雷诺数Reg不小于30 841.80;若质量流速不能保证Reg大于32 323.21,则相比维持当前所能达到的转速,保持较低的转速能获得更好的换热效果;在能够保证Reg大于32 323.21的情况下,维持Reg的取值满足式(19)的条件可获得最大的换热系数.
当蒸汽质量流速一定而转速可调时,若质量流速对应的Reg小于26 286.71,保持区间内最低转速可以获得最佳换热效果;当Reg大于26 286.71时,保持区间内最高转速可令换热系数达到最大.当转速与蒸汽质量流速均可在当前区间内调整,则同时保持区间内最大的转速和质量流速方可获得区间内的最优换热系数.
然而对于实际生产,除了考虑以上因素外,还要考虑工艺、能耗、设备损耗等因素,以获得最符合实际情况的最优换热系数.
4 结论
综上所述,可得出如下结论:
(1)蒸汽的质量流速较低时,转速对于换热性能的提升影响很小;而在高蒸汽质量流速下,转速对于换热性能的提升影响要大于蒸汽质量流速的影响,蒸汽质量流速的增大只有在转速达到一定值的情况下才有意义.
(2)当转速一定时,质量流速应至少保证气相雷诺数Reg不小于30 841.80;当质量流速不能保证Reg大于32 323.21时,转速应当降低;在能够保证Reg大于32 323.21的情况下,维持Reg的取值满足对应的线性关系,这样可获得最优的换热系数.
(3)当蒸汽质量流速一定时,若质量流速对应的Reg小于26 286.71,保持区间内最低转速可以获得最佳换热效果;当Reg大于26 286.71时,保持区间内最高转速可令换热系数达到最大.
(4)烘缸的实际蒸汽质量流速与转速应为获得尽可能高的换热性能服务,但也应在考虑实际工况与成本问题后,做出最优方案.
