核心立结构 整体建概念
——整合视域下“万以内数的认识”单元教学的思考与实践
2023-12-06沈丹妮吴利敏
沈丹妮, 吴利敏
(1.宁波市江北外国语学校,浙江 宁波 315000;2.湖州师范学院 理学院,浙江 湖州 313000)
0 引 言
2022版《新课程标准》强调了数概念本质的一致性.近几年,“单元整合”“整体视域”等热词进入了一线教师的课堂.借此契机,笔者以人教版二年级《数学》下册第七单元“万以内数的认识”为例进行单元内容、知识版块的整合教学,以期在思考中优化教学,在实践中突破困境,从而让教学更有厚度,让学习更有深度.
1 深度剖析,现状透视
核心素养导向的教学,强调课程内容的内在联系,突出课程内容的结构化,探索发展学生核心素养的路径[1].因此,核心素养导向的教学要体现结构性、整体性和一致性.“整数”的学习离不开数位、计数单位、位值制、十进关系这些概念,而且“小数与分数”的学习依然以计数单位为核心.可见,整数、分数、小数的关系是通过计数单位这个核心概念关联的,计数单位是打通数概念学习隔断墙的核心知识.在整数认识范畴教学中,“万以内数的认识”单元更为全面、正式、系统地引入了计数单位、数位等概念.因此,本单元的学习举足轻重,上承百以内数的认识,下启更大数、小数、分数的认识.然而,目前的教学仍存在以下问题.
1.1 学教起点差异化,矛盾凸显
学生已有的认知水平是开展教学的起点,因此教师需要基于学习前测对学情展开精准分析,进而思考教学方向.笔者对宁波市某学校二年级学生(80人)进行前测,测试内容为万以内各数的认识及相关计算,结果见表1.
现实起点:分析表1发现,学生对万以内数的大小比较、写数、近似数等有较高的学习起点.这是基于学生对“百以内数的认识”内容学习经验的积累和学习方法的迁移自然生成的.然而,学生对“千”“万”这些更大计数单位的表象建立是非常模糊的.随着计数单位的扩展,学生对相邻计数单位之间的十进制进率并不清晰,不确定是否可以将十进制关系正向迁移至较大的计数单位.虽然学生能够计算整百、整千数的加减法,但在算理理解上并没有建立计数单位与运算的本质关联.可见,“千”“万”这些计数单位的出现,给学生对数概念意义的理解带来了一定的挑战.

表1 前测结果反馈表
逻辑起点:教材将万以内数的认识、整百整千数的加减、解决问题作为单元的重难点,但没有凸显“千”“万”作为新的计数单位这一难点,对“千”“万”的认识和理解也没有强化.如果教师仅局限于教材,而忽视学生的现实起点,均衡用力安排教学,就会造成万以外更大计数单位教学的断层,从而导致学生无法用计数单位这一核心概念来认识小数和分数,以及他们之间的内在关联,也不利于学生结构化思维的形成.
1.2 教材内容模式化,感知模糊
小学数学整数概念在教材中的分布较分散,各知识点之间存在着许多交叉和相似.整数教学分解到每一册、每一节课中,以一个个知识块的方式呈现.这一螺旋式的呈现让学生经历以“一”“十”“百”“千”“万”为单位的学习历程,感受逐一计数和按群计数,在计数中构建新的计数单位.但在每一阶段的学习中,教材的呈现都是均衡分布的.而从前测学情可知,学生对“千”“万”计数单位的感知容易与之前的计数单位混淆,仅靠一课时的学习是远远不够的.本单元的教学内容是对计数单位这一核心概念的理解、运用与应用.这些内容在知识结构的内在序列上是整体贯穿、紧密相连的,而教材却将他们分多课时进行教学,无疑使原本点状的知识更加分散,打破了学生认数体验的完整性.
模式化的内容分布,往往会使教师在教学结构性上缺乏完整性,内容上缺乏对知识的整体把握,忽视“点”背后知识之间的本质关系.教学内容的模式化也容易导致教学的模式化,从而导致学生难以借助计数单位开展主动学习,无法将知识结构化,学生的学习无法达到见木又见林的效果.
1.3 学习材料固定化,体验单薄
纵观整数教学教材对学习材料的使用,笔者发现本单元还是局限于小方块和计数器.对“一”“十”这样较小的计数单位,学生在生活中经常用到,数感相对容易建立,因此能够较好地利用小棒展开学习.而“百”“千”“万”这样的计数单位的认识借助方块或计数器也确实简洁、实用,但由于学生在生活中用得较少,所以无法充分感知数的具体表象.因此,学习材料的固化、单一会使学生的体验单薄、局限,不利于数感的形成与发展,也很难将抽象的数逆向转化到生活中.片面固定的学具难以帮助学生经历“具象—抽象—具象”的数概念学习的过程.
2 深度构思,聚焦整合
单元整合并非简单地将几部分内容删减或叠加,而是需要关注各知识点的共同要素,打破课时甚至单元之间的壁垒,重新安排学习内容,从而改变原有的教学体系,为学生提供一个更加开放、系统的知识体系.
2.1 把握根本,重组单元例题
在“万以内数的认识”中,虽然数概念的“细枝末节”较多,无论是数数、数的组成、数的读写、大小比较,还是整百整千数的加减法,都是指向同一个核心概念——计数单位.基于此,笔者立足这一核心概念,将“万以内数的认识”的相关例题进行重整,见图1.
2.2 建构框架,重整单元序列
确定本单元两大核心内容,即认识计数单位和理解计数单位,并根据教材编排确定计数单位的运用教学,见表2.

表2 整合前后的课时安排
重整后,本单元以“计数单位”为核心,以认识计数单位、理解计数单位、运用计数单位为脉络,以“认识千、万”“万以内数的读写”为重点课例,以“生活中的千千万万”为主题活动课,兼顾解决问题能力的培养和计算技能的训练.除新授课、练习课、复习课外,还设计了“主题活动课”“反馈与评价”“教学跟进”.“主题活动课”结合数概念展开实践,以激发学生学习兴趣,培养学生数感;“反馈与评价”检测评价教与学;“教学跟进”反馈检测结果,以及时查漏补缺,适当拓展.
2.3 锚定方向,重制单元目标
基于教学内容统整及学生起点,保证内容完整,体系螺旋上升,笔者重新调整了单元目标,见图2.

图2 重整后的单元教学目标
3 策略优整,笃行致远
单元整合并非一蹴而就,它需要以核心素养为导向,基于学生立场,从整体视角深入研究教材,紧扣数学本质,对知识进行系统地联结、统整、重构,更需要在实践中探索课堂教学改革下的有效策略与方法.
3.1 打通素材壁垒,借势而为
3.1.1 学材对比,沟联本质
学生的作品是教学的优质素材,显示学生的真实起点,接近认知发展区.通过对不同学生作品的对比与研讨,教师更能够顺应学生的认知结构展开教学,从学生作品中来再到学生认知中去,将学生认知的“平衡—不平衡—平衡”充分可视化.
例如,在“认识计数单位千、万”的课堂导入中,“用你喜欢的方式表示1273”的学生典型作品见图3.

图3 “用你喜欢的方式表示1273”的学生典型作品
教师可以让学生分别介绍自己的想法,引导观察比较各种方法之间的异同:①号作品用小方块一百一百地计数,但对计数单位“千”没有从“百”主动迁移过来;②号作品已初具“千”为计数单位的雏形,感受到用计数单位的累加来表示数的意识;③号作品最接近计数器的模型,意味着学生通过前期“百”“十”“一”计数单位的学习,能够对更大的计数单位产生正向迁移;④号作品虽然是错误的,但是在③号作品的基础上更显抽象与简洁.4个典型作品真实地反映出学生对“千”这一新计数单位从模糊到清晰再到抽象的过程,思维水平逐级进阶,充分展现出学生立场的“真”、素材的“实”.
3.1.2 横纵融合,内化核心
提供材料:大米、黄豆、小方块,让学生数一数、摆一摆,表示出1,10,100,1 000,10 000.
同类异数:让学生用同一种材料表示不同的数,通过数数表示出1,10,100,1 000,10 000,以此作同种材料的横向对比,深刻感受计数单位的视觉和体验冲击.
同数异类:让学生用不同种材料表示1 000,10 000,通过纵向对比感受用不同材料表示相同数的区别和联系.
教师充分利用材料让学生进行横向和纵向对比分析,在同类材料的不同数量中产生对不同计数单位形象的认知;在不同类材料摆同一个数中,让学生自然形成更清晰的计数单位表象.
3.2 优化教学路径,顺势而行
3.2.1 多元表征,丰富认知
对数的多元表征有助于学生丰富对数的表象的建立,尤其对“千”“万”这样的计数单位及大数的现实意义,通过对不同的表征形式进行整合,有利于提升学生的整体感知,丰厚认知,发展数感.
生活经验表征:学生学习“数”的概念是一个主动的、复杂的过程,教学需要随着学生知识经验的不断累积而加以深入和扩展[2].所以,教师应积极利用生活中的数学素材,让学生对数学产生熟悉感和亲切感;将教学内容与现实生活相联系,让学生能够真正理解“数”的概念并能正确运用.
教材中计数器、方块图的表征方式单一,教师可通过深入挖掘生活中的素材进行表征,拓宽学生数的认识.例如,在主题活动课中,教师可围绕“1 000粒黄豆有多少?”这个任务驱动展开活动探究,让学生经历数数的过程,进而通过呈现与对比,多元感受一千.
直观模型表征:教学并不是教教材,而是用教材,教材中对“千”“万”的认识局限于小方块,虽然提供了素材,但依然让学生难以对一千、一万有强烈的感知.学生在生活中缺乏对数大数的经验,数100、200、300……的感觉与数1,2,3……的感觉差不多,对大数满十进一也是模糊的.因此,教师可将1 000个小正方体组成的大正方体拆成一面一面,变成一面方块墙,见图4.

图4 方块墙表征数值
给每个小正方体按顺序标上数字,那么第一个面就是1~100,有100个数.学生根据“第二个面要用到哪些数?”依次数出“101,102,103……109,110”,并用计数器演示“满十进一”.再依次数出“111,112……119,120”,并用计数器同步演示.通过全班齐数、同桌数的方式,将教材中的计数模型进行联通,不仅能使计数单位的表象更清晰,还能使计数单位间的进率更外显.

图5 计数器演示“满十进一”
数学符号表征:数学符号表征是思维发展的高阶水平,不需要借助图形或模型来理解数的意义,可以让学生个别说、同桌说、集体说“( )个千,( )个百,( )个十和( )个一组成( )”,用数学语言表征数的组成,让学生写数、读数进行数字表征.
3.2.2 化错为“措”,生成位值
“化错”是教师利用合适的方法和科学的手段,促使学生意识到自己的学习错误,并积极从自身寻找错误的原因,将错误转化为学习动力,促进学生进步的教学策略.例如,在教学认识“千”“万”中,教师可通过让学生自主观察1273作品,暴露学生起点的不完整性和错误.对学生错误的呈现结果,教师可通过化错让学生当堂评价和及时修正优化,从而促使学生立场学习的自然生成.
师:这幅作品(图6),你能看懂吗?

图6 数值演示作品图
生1:可以,合起来就是1372.
生2:有错误,这里的70画得比200还要大!
师:有数位,但计数单位之间的关系没有正确表示,数学追求严谨,怎么纠正?
学生同桌讨论,尝试修改.
生:把1 000平均分成10份,1份就是1个百,2份就是200;把100平均分成10份,1份就是1个十,7份就是70;最后把10平均分成10份,1份就是1个一,3份就是3.
用图呈现平均分的过程,见图7.

图7 平分过程图
追问:从自主创造的这张图中,能得到什么?
生1:10个百是一千.
生2:相邻两个计数单位的进率是十[3].
学生对“满十进一”虽然难以正向迁移,感受模糊不清,但教学就是让学生经历从模糊到清晰的过程,让学生将错就错达到柳暗花明,将旧知调动起来用于新知探索,进而深刻理解位值原理.
3.3 借力素养立场,乘势而起
3.3.1 数形互估,发展数感
估计是发展学生数感的重要方法.数与形密不可分,通过“以形估数”“以数估形”,让学生充分理解“数”和“形”的双重特征,实现彼此转化和融合,才能更好地发展数感[4].
以数估形:如图8所示,让学生根据已知价格的手机和“荣耀”手机价格的特征,估计这部手机的价格.学生通过数的组成可以快速判断出数的大小,再根据图形的高度展开思考、想象、比划……多种方式展开估计,估出数后再进行整体观察,感受数的大小,进一步完善数的认知,多层次地发展数感.
以形估数:根据已知图形的高度和数的部分特征,进行推断和估计,并展开说理,在数与数的比较、思考、辨析中发展数感,见图9.
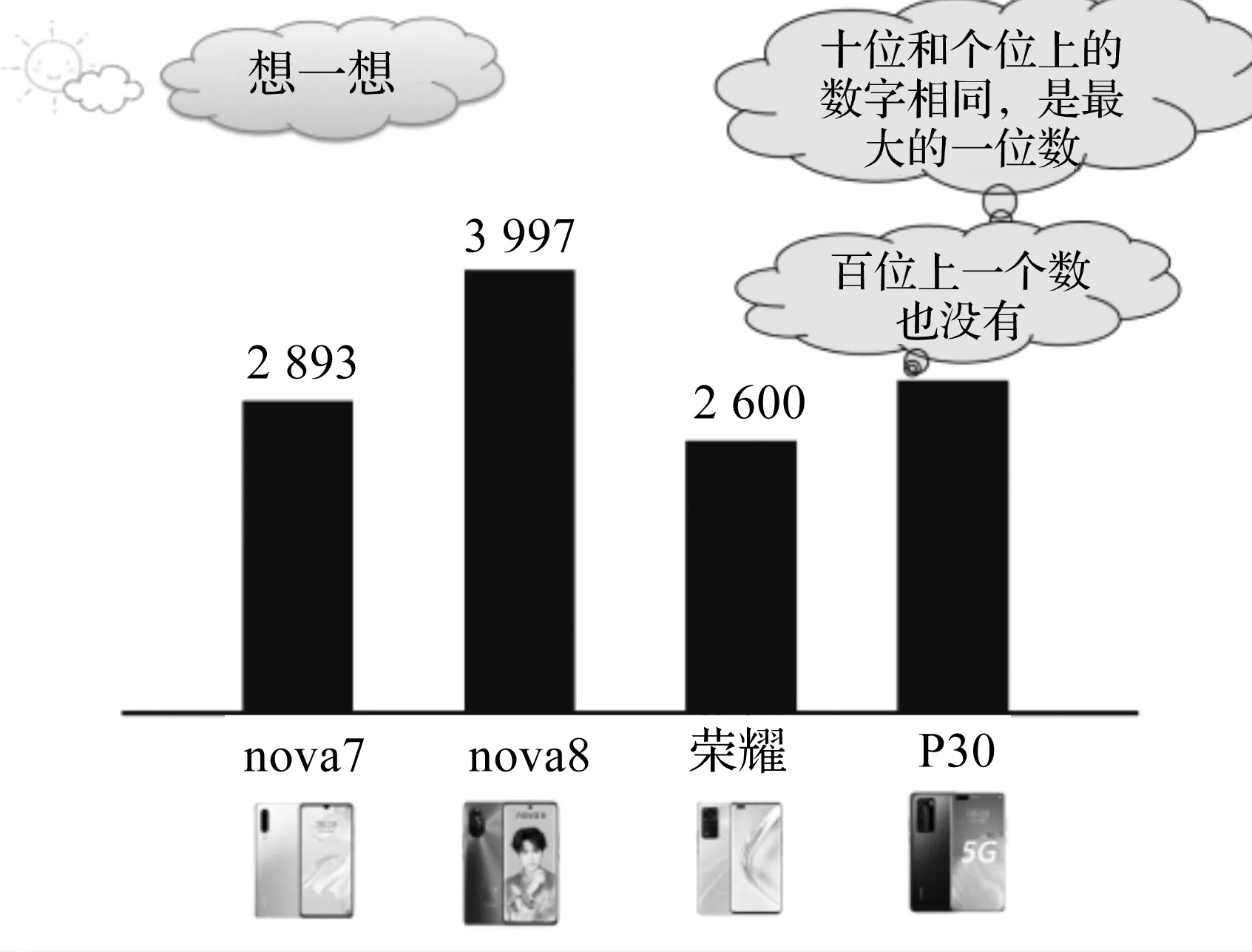
图9 题图
总之,数形互估能够正向与逆向共通,操作与思辨并行,多角度地借助形与数进一步发展数感.
3.3.2 多维转化,培养推理
数学是一门推理的学科,而通过多种维度的转化可以将推理的过程可视化.在认识“万”的过程中,如果只通过观察和想象,是难以更好地建立表象的.因此,在10 000的操作活动中,教师可鼓励学生借助100,1 000来展开推理.为让学生更好地体验推理过程,利用“称重大米”将“数”转化成重量,让学生根据1 000粒大米的重量推出10 000粒大米的重量.同理,“平铺大米”则是将“数”转化成面积,“瓶装大米”则是将“数”转化成体积,通过这样可视化的过程培养学生的推理意识[5-6].
4 结 语
将“计数单位”这一核心概念立于核心位置,开展“万以内数的认识”的单元整体教学,不仅可以让教师将零散的知识点串联成线,还可以让学生对“数”的认知呈现可迁移、可持久的学习状态,更有利于学生建构完整的“数的认识”知识体系,通过有结构的教、有关联的学,实现深度学习.
