Vibration analysis of circular Janus MoSSe plates

Liu Xinjie Wang Lifeng

(State Key Laboratory of Mechanics and Control for Aerospace Structures,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

Abstract：The vibration behavior of Janus monolayer molybdenum sulfoselenide (MoSSe) was studied based on molecular dynamics (MD) simulations and the finite element method (FEM).MoSSe plates were simulated by FEM through the incorporation of intrinsic strain caused by lattice mismatch to the double-layer plate model.The vibrations of circular MoSSe plates with free boundaries and a clamped edge were determined by MD simulations and FEM.In addition,the effects of plate size,strain,and pressure on the natural frequency of the plates were investigated.The results showed that the natural frequency of the circular MoSSe plate with free boundaries gradually decreased with increasing plate size.Furthermore,a significant discontinuity in frequency was observed due to bowl and tube warpage when the diameter reached 8.6 nm.The MD simulation and FEM calculation results were consistent in terms of the natural frequencies of the circular MoSSe plates of different sizes.In addition,the effects of strain and pressure on the natural frequency determined by the two methods were consistent for small deformations.The vibration of the MoSSe plate could be well predicted by the double-layer plate model.

Key words：Janus monolayer molybdenum sulfoselenide (MoSSe); molecular dynamics (MD); warpage; natural frequency

Since the discovery of graphene,two-dimensional (2D) materials have attracted considerable research attention owing to their remarkable mechanical,electronic,and thermal properties[1-8].In addition to graphene,2D transition-metal dichalcogenides (TMDs)[9-12]have garnered considerable attention owing to their unique physical and chemical properties.The mechanical,electrical,optical,and thermal properties of molybdenum disulfide (MoS2),a typical TMD material,have been extensively explored[13-16].In recent years,2D heterostructures composed of vertically stacked 2D materials with distinct properties have exhibited novel characteristics[17-18].Molybdenum sulfoselenide (MoSSe) possesses a structure similar to heterostructures,even though it is composed of a single material.In a recent study,Lu et al.[19]completely replaced the top-layer S atoms in MoS2with Se atoms.The Janus structure of MoSSe was confirmed through scanning transmission electron microscopy and energy-dependent X-ray photoelectron spectroscopy.The presence of vertical dipoles was confirmed through second harmonic generation and piezoresponse force microscopy measurements.Zhang et al.[20]controlled the sulfide action to replace the top Se atoms of monolayer molybdenum diselenide (MoSe2) with S atoms,while the bottom layer of Se atoms remained unaffected.Through this method,a Janus monolayer MoSSe structure was formed,comprising three layers of atoms from top to bottom,namely sulfur,molybdenum,and selenium.Idrews et al.[21]used hybrid density-functional theory calculations to investigate Janus monolayers and their associated van der Waals heterojunctions.They discovered that MoSSe is a direct-bandgap semiconductor.Indirect-bandgap semiconductors can be converted into direct-bandgap counterparts using external electric fields.In direct-bandgap semiconductors,electrons can directly excite or de-excite by the absorption or emission of photons with no involvement of phonons in the processes.This property renders them more suitable for manufacturing optoelectronic devices.Dong et al.[22]investigated the planar and vertical piezoelectric properties of monolayer and multilayer MXY structures (where M=Mo or W,and X/Y=S,Se,or Te) based on ab initio calculations.Under substrate influence,uniaxially strained MXY structures exhibited high in-plane piezoelectric polarization but significantly weaker out-of-plane piezoelectric polarization.Conversely,laterally strained multilayer MXY structures exhibited substantial out-of-plane piezoelectric polarization.These studies highlighted the applicability of MXY structures in smart nanodevice applications.Kandemir et al.[23]employed first-principle computations to investigate the structural and phononic properties of MoSSe monolayers.They utilized out-of-plane anisotropy to demonstrate the unique vertical pressure effect on the vibrational characteristics of Janus materials due to the asymmetric structure of Janus MoSSe monolayers.Pham et al.[24]developed ultrathin graphene/MoSeS and graphene/MoSSe heterostructures and studied their structural and electrical properties and the effect of vertical electric fields on these heterostructures.These designed heterostructures were intended for applications in nanoelectronic and optoelectronic devices.

Studying the vibration of nanoscale structures is imperative owing to the crucial role of vibration behavior in the functionality of smart nanodevices.Jiang et al.[25]investigated the nanomechanics and vibration behavior of graphene sheets,employing a 2D plate model that accounted for varying sizes and boundary conditions.The simulation results highlighted the accuracy and efficiency of the 2D plate model,demonstrating its potential as a promising alternative for modeling nanomechanics and analyzing the vibration of graphene sheets when compared with several well-established experiments and equivalent theoretical models.Akgöz et al.[26]investigated the free vibration of a single-layered graphene sheet positioned on an elastic matrix.They derived the governing equation of motion using the thin plate theory in conjunction with Hamilton’s principle.Kitipornchai et al.[27]employed a continuum model to assess the vibration of multilayered graphene sheets,revealing that varying the number of layers can lead to various resonance modes.Zhang et al.[28]explored the vibration frequency of rippled single-layered graphene sheets and identified that introducing functional groups,defects,carbon nanotubes,and surface wrinkles can induce significant frequency shifts in pristine single-layered graphene sheets.Zhang et al.[29]investigated the thermal vibration of rectangular monolayer black phosphorus based on an orthotropic plate model and molecular dynamics (MD) simulations.MD simulations and the orthotropic plate model,combined with the law of energy equipartition,provided insights into the root-mean-square amplitude of rectangular monolayer black phosphorus.Through MD simulations and a continuous plate model,Yi et al.[30]investigated the vibration behavior of single-layered hexagonal boron nitride and explored the effect of an electric field on the intrinsic frequency.Zhang et al.[31]employed the circular Mindlin plate model to analyze the vibration of circular single-layered MoS2.The findings indicated that for very small plate sizes,particularly at higher-order frequencies,the natural frequencies computed by the Mindlin plate model aligned more closely with those determined by the MD method than those computed by the Kirchhoff plate model.Thus,it is necessary to reveal the dynamic behavior of the Janus monolayer MoSSe structure.

To the best of our knowledge,the vibration behavior of Janus MoSSe has not been studied yet.Therefore,MD simulations and the finite element method (FEM) are employed to investigate the vibrations of Janus monolayer MoSSe,considering free-boundary and clamped-edge conditions.In addition,the effects of size and the initial stress are studied.

1 Vibration Analysis of the MoSSe Plate with MD Simulation

The atomic structure of Janus monolayer MoSSe features a sandwich-like arrangement with selenium,molybdenum,and sulfur atoms spanning from the upper to lower layers (see Fig.1).The Stillinger-Weber (SW) potential,recently formulated for various MX2structures (M=Mo,W; X=S,Se,Mo) and their alloys and lateral heterostructures,is adopted here[32].Thus,the interatomic interactions within the Janus monolayer MoSSe are described using the SW potential function.

(a)

The mechanical properties of the monolayer in the zigzag and armchair directions are determined through MD simulations using a square sheet under periodic boundary conditions; the monolayer thickness is set at 0.324 nm.The model is subjected to stretching along a single direction,and during this process,stresses in the tensile direction and strains in the nontensile direction are recorded.The resulting stress-strain curves for the armchair and zigzag directions are shown in Fig.2(a).The red solid line represents the stress-strain curve for stretching along the armchair direction,while the black dashed line corresponds to stretching along the zigzag direction.The relationship between strains along the armchair and zigzag directions during uniaxial tension is shown in Fig.2(b).The red curve shows the relationship between the zigzag-direction strain (vertical coordinate) and armchair-direction strain (horizontal coordinate) during stretching along the armchair direction.Furthermore,the black curve shows the relationship between the armchair-direction strain (vertical coordinate) and zigzag-direction strain (horizontal coordinate) during stretching along the zigzag direction.Within the linear range,stresses in both directions exhibit nearly identical behavior at equal strains.For small tensile strains,Poisson’s ratio values are almost identical for both directions.For simplicity,the material can be treated as isotropic.Young’s modulus is taken as the average of the two directions,yielding 230.4 GPa,and Poisson’s ratio is similarly averaged at 0.23.

(a)

The natural frequencies of the circular MoSSe plate with a clamped edge and free boundaries can be determined using the MD software Large-scale Atomic/Molecular Massively Parallel Simulator[33].Initially,the boundaries of the MoSSe plate are set as free boundaries.The equilibrium state of the structure is achieved by the steepest descent method combined with the conjugate gradient approach for energy minimization.Thereafter,MD simulations are performed using the NVT ensemble,and a temperature of 300 K is maintained using a Nose-Hoover thermostat with a time step of 1 fs for 5 ns.During the calculation related to the free-boundary case,the linear and angular momentums of the model are constrained to zero to avoid rigid-body displacements.The positions of the selected MoSSe atoms are recorded at every 100 steps.Subsequently,vibrational frequencies are computed by fast Fourier transformation (FFT).Fig.3(a) shows the out-of-plane displacement of a sulfur atom selected from the MoSSe circular plate with a clamped edge.The thermal vibrational spectrum corresponding to the atom’s displacement derived by FFT is shown in Fig.3(b).Each peak in the spectrum represents a natural frequency of the MoSSe plate.In addition,the figure shows the vibration modes obtained by MD simulation.A periodic force is applied to the MoSSe plate with a frequency similar to the plate’s natural frequency.Once a steady state is reached,vibration modes corresponding to the natural frequency can be observed.

(a)

During computations with free-boundary conditions,with the increasing diameter of the circular plate,the natural frequencies of each order gradually decrease while maintaining a relatively continuous trend.However,a discontinuity arises when the diameter reaches 8.6 nm (see Fig.4).The MD simulation reveals alterations in the morphology of the MoSSe plate after relaxation.As the model size increases,the warping transforms from a uniformly curved bowl shape into a tubular structure with warped ends,and the extent of warping intensifies.The MD simulation results indicate that at a diameter of 8.6 nm,a shift from bowl-like warping to tubular warping occurs.For diameters greater than 9.0 nm,a complete transition to tubular warping occurs.To validate the rationality of this outcome,a continuous medium model is employed to simulate the MoSSe plate,and its vibration frequency is computed for comparison with the MD simulation results.

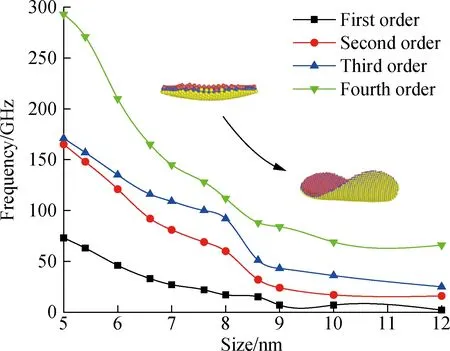
Fig.4 First-to fourth-order natural frequencies of molybdenum sulfoselenide circular plates with different diameters

2 Continuum Mechanics Model for Vibration of the MoSSe plate

From the calculations discussed in the previous section,a discontinuity is observed in the natural frequencies of the MoSSe circular plate with free boundaries.Furthermore,two distinct warping morphologies,bowl and tubular warping,are identified.FEM analysis is conducted to investigate the vibration behavior of the MoSSe plates.For meshing,a free tetrahedral mesh is used.Convergence results are achieved with regular or high meshing densities,where the minimum cell size is set to 0.04 nm,maximum cell size to 0.55 nm,and maximum cell growth rate to 1.4.A circular composite plate comprising of two sublayers is used to analyze the warpage of the Janus monolayer MoSSe structure.These two sublayers are closely integrated,forming a unified structure.The upper layer represents the molybdenum-selenide structure,with a thickness of 0.171 nm,while the lower layer represents the molybdenum-sulfur structure,with a thickness of 0.153 nm.The strains due to lattice mismatch (εMo-S=(αMoS2-αMoSSe)/αMoS2,εMo-Se=(αMoSe2-αMoSSe)/αMoSe2) are incorporated into the corresponding sublayer as the initial state[34-39],whereεMo-SandεMo-Serepresent the strains in the Mo-S layer and Mo-Se layers,respectively,andαMoSSe,αMoS2,andαMoSe2represent the lattice constants of monolayers MoSSe,MoS2,and MoSe2,respectively; the relevant parameters are listed in Tab.1.After warpage,the natural frequencies of the plates with different boundary conditions are calculated.The FEM calculation results show identical transformations of the warpage morphology (see Fig.5).Both methods yield the same warpage patterns and dimensions of warpage-pattern changes,which verifies the rationality of the model.The natural frequencies of the plates with free boundaries calculated by these two methods are shown in Fig.6.The first four natural frequencies obtained by both methods decrease with increasing plate size.When the diameter of the MoSSe circular plate reaches 7 nm,the second-and third-order frequencies obtained by FEM overlap.

Tab.1 Material parameters

(a)

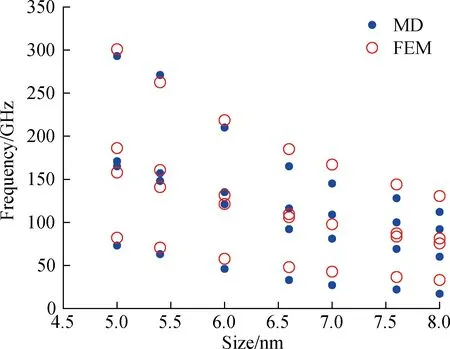
Fig.6 First-to fourth-order natural frequencies of the molybdenum sulfoselenide shallow spherical shell with free boundaries

The warpage morphologies change when the diameter of the circular plate reaches 8.6 nm,similar to the calculation results with free-boundary conditions.To analyze circular plates with clamped edges,the diameter is maintained at <8.6 nm to ensure the persistence of bowl-like warping.The calculation results of the first eight natural frequencies of the shallow spherical shell,which is formed by warping a circular plate with a diameter of 7.5 nm,are shown in Fig.7.The frequencies obtained by the two methods are consistent.Furthermore,the vibration modes are obtained by FEM.

Fig.7 First eight natural frequencies and modes of the shallow spherical shell formed by warping the circular plate of the Janus MoSSe structure with a diameter of 7.5 nm

To further investigate the effect of plate size on the vibration frequency,circular plate models of MoSSe with diameters of 4.5 to 8.1 nm are established.The natural frequencies of the MoSSe plates with clamped edges are shown in Fig.8.The natural frequency decreases with the increasing diameter of the shallow spherical shell.Furthermore,the discrepancy between the results obtained by the two methods decreases with increasing plate size.Overall,the two methods provide consistent results,and the double-layer plate model can well predict the warpage and natural frequency of the MoSSe circular plate.

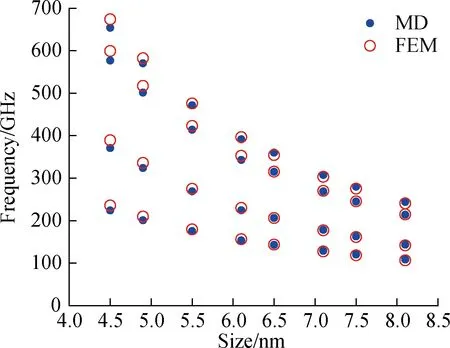
Fig.8 First-to fourth-order natural frequencies of the molybdenum sulfoselenide shallow spherical shell with a clamped edge

3 Vibration Analysis of the Circular MoSSe Plate with Initial Stress

In this section,the effect of the initial stress on the natural frequency of the MoSSe circular plate after the warpage is investigated.

To analyze the effect of tension on the vibration of the Janus MoSSe structure,a MoSSe plate model with a diameter of 7.5 nm under different strains was established.Thereafter,uniaxial and radial stretching cases were investigated.Uniaxial stretching was performed along the armchair and zigzag directions (see Fig.9(a)).The natural frequencies of the MoSSe plate with a clamped edge after uniaxial stretching are shown in Fig.9(b).A new frequency emerges from the original second-order frequency due to the asymmetry introduced by the strain in the two orthogonal directions.In the unstretched case,the properties along the zigzag and armchair directions exhibit similarity.Therefore,the second-order frequencies corresponding to the zigzag and armchair directions are the same.However,stretching induces an asymmetry between these orthogonal directions,leading to differences in natural frequencies.Thus,the original second-order frequency splits into a lower and higher natural frequency.The difference between the second-and third-order frequencies gradually increases with increasing strain.Furthermore,the fourth-order frequency also gradually increases,but the first-order frequency decreases until the strain reaches 0.04 and then gradually increases.Stretching along the armchair and zigzag directions yields the same effects on the natural frequency.Fig.10 shows the effect of radial stretching on the natural frequency.The first-order frequency decreases until the strain reaches 0.15 and then gradually increases,and higher-order frequencies increase as the strain increases.Although the same trend is observed in the FEM calculations,the consistency between the two results is predominantly maintained only when the strain is small.For larger strains,the frequencies determined by FEM increase at a higher rate than that determined by MD,and when the strain reaches 0.03,a substantial discrepancy exists between the two results.

(a)

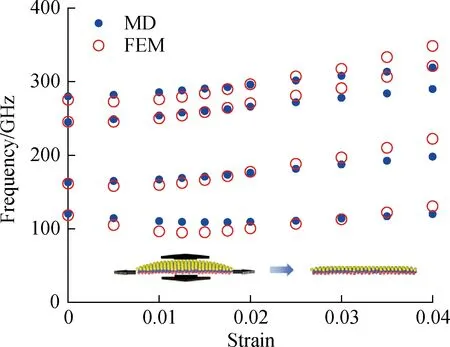
Fig. 10 Effect of radial stretching on the natural frequency

Fig. 11 First three natural frequencies of the molybdenum sulfoselenide shallow spherical shell with z-directional pressure

Finally,the effect of pressure on the natural frequency is investigated.The boundary of the plate is fixed after sufficient warping before pressure application.The frequency obtained by the MD simulation dramatically increases in the pressure range of-0.073 to 0.146 GPa and slowly increases for pressure greater than 0.146 GPa (see Fig.11).When the pressure value is positive,the pressure aligns with the upward direction in Fig.11,and when the value is negative,the pressure aligns with the downward direction.Under low pressure values,the results obtained by the two methods are consistent,and under large pressure values,a substantial discrepancy occurs between the two results.

4 Conclusions

1) The analysis of vibrations in the MoSSe circular plate with free boundaries reveals a distinct frequency discontinuity.This phenomenon is associated with the presence of two warpage patterns,a finding that is successfully reproduced in FEM calculations.

2) The natural frequencies of the MoSSe circular plate with a clamped edge obtained by the MD method and FEM are consistent.The discrepancies between the results of these two methods decrease with the increasing size of the MoSSe structure.The comparison reveals that the vibrations of the circular MoSSe plate are well predicted by the double-layer model.

3) The effects of strain and pressure on the natural frequency are also investigated.The frequencies obtained by FEM and the MD simulation are consistent under sufficiently small deformations.However,under larger deformations,the frequencies determined by FEM are higher than those determined by the MD simulation.