基于遗传算法优化的模糊PID恒温水浴控制系统*

陈月婷 马晓 王飞 赵玉成 / .山东省计量检测中心；.山东省计量科学研究院

0 引言

恒温水浴被广泛应用于各类温度计、密度计、黏度计等计量器具的检定和校准，其温度控制系统控制加热装置和制冷装置对槽体内液体进行加热和制冷，并辅以循环系统确保槽体内液体达到并保持设定的温度[1]。作为一种温度实验设备，其温度偏差、温度均匀度和波动度是恒温水浴的主要性能[2-3]。而对温度控制系统而言，调节时间、超调量和稳态误差是评价温度控制系统的重要指标。传统的PID 控制虽然能够实现恒温控制，但是存在一些无法克服的缺陷，如：无法处理温度信号延迟滞后、超调量过大等问题，致使温度控制准确度不高，调节时间过长。

近年来，许多专家将模糊控制和传统比例积分微分控制（proportional-integral-derivative control，简称PID 控制）相结合，充分利用模糊控制对系统模型的依赖性小、响应速度快等特点，弥补传统PID控制的不足，取得了较好的效果[4-5]。但模糊PID 控制的模糊控制规则往往依赖专家经验或者通过大量实验获取，这也限定了上述方法的应用。

针对上述问题，本文提出了一种基于遗传算法（GA）的模糊控制规则优化方法，以温度控制系统的调节时间为评价函数，通过迭代优化获取温度控制效果较好的模糊控制规则。该方法可有效降低模糊控制规则对专家经验的依赖性。仿真实验表明，在模糊PID 温度控制中采用基于遗传算法优化的模糊控制规则，可在提高动静态特性和控制准确度的同时，提高恒温水浴的工作效率。

1 恒温水浴温度控制系统的组成与工作原理

恒温水浴温度控制系统的功能主要包含对槽内液体的调温和恒温。本设计选用的主控制器为可编程逻辑控制器（简称PLC 控制器），其结构主要包括：PLC 控制器、显示/设置单元、温度变送器和温度传感器、循环装置、加热装置和制冷装置等[6]。恒温水浴的控制原理图如图1 所示。

图1 恒温水浴的控制系统原理

其中，PLC 控制器获取温度传感器采集到的液体温度，计算液体温度与显示/设置单元设定温度值的偏差和温度偏差变化率，进一步利用模糊控制规则，通过模糊PID 控制算法得到PLC 的输出控制信号，使用固态继电器的通断实现对加热装置、制冷装置和循环装置的控制。具体工作原理为：当前采集的温度值低于设定值时，PLC 根据存储的模糊控制查询表，控制加热装置工作，提高液体的温度；当前温度值高于设定值时，PLC 根据存储的模糊控制查询表，控制制冷装置工作，降低液体的温度。此外，为保证恒温水浴内液体温度的均匀性，在加热装置或制冷装置工作的同时，打开循环装置，而如果当前温度值在设定值上下波动幅度很小，则加热、制冷装置循环工作，使恒温水浴内液体温度经过控制系统调节后达到设定的温度值。

根据上述恒温水浴的工作过程，可以看出，用于PLC 对执行机构控制信号的模糊控制规则在控制系统中起到非常重要的作用。为减少模糊控制规则对经验的依赖性，有必要设计一种优化算法，实现智能获取最优的控制规则，这是本文研究的主要内容。

2 模糊控制

将恒温水浴的当前液体温度与设定温度的差值(E，即温度偏差）和温度偏差变化率（EC）作为模糊控制器的输入，PLC 对执行机构的控制信号（U）作为模糊控制器的输出[7-8]。因此，模糊控制规则表可表述为如式（1）所示的3 元组。

考虑恒温水浴的实际工作情况，假设E和EC的变化区间为[-70 ℃,70 ℃]，为满足控制准确度和便于计算，E、EC和U模糊集论域定义为[-6,6]，共13 个等级；模糊量的语言值设为7 挡，即：NB、NM、NS、ZO、PS、PM 和PB。

从上述论述可以看出，所设计的模糊控制规则表设定了温度控制系统49 种输入，而每种输入对应的输出为7 种。即将模糊控制规则看作模糊控制器的解，其值域（解空间）的规模为343。本文采用遗传算法求解满足控制要求的模糊控制规则表。

采用Mamdani 模糊推理方法，求解模糊的过程选用重心法，将推算结果整理成模糊控制查询表。

3 基于遗传算法模糊规则的优化方法

遗传算法不需要建立参数和目标函数的显示关系，仅仅通过适应值函数对控制参数的评价来判别空间解的优劣[9-10]，常用于求解工业问题的近似解。在本文中，利用调节时间构造适应值函数评估解的质量，采用随机多点交叉和随机多点变异保持样本的多样性。

3.1 遗传编码和解码

本文是针对U进行编码优化。如前所述，U包含7 个模糊状态，因此，U可采用3 位二进制串进行编码。由于PLC 的输入信息包含E和EC，且每个输入包含7 种模糊状态，所以模糊控制规则共定义了49 种模糊状态的输入组合，因此，将模糊控制规则表定义为遗传算法的个体，其编码长度为147（49×3）。对应的解码过程为将长度为147 的二进制编码，按长度3 解码为49 个模糊控制器的输出状态值，其解码表达式如式（2）所示：

式中：s——对应解码后的模糊状态；

bi——二进制串第i位上的值（0 或1）

需要注意的是，式（2）的值域为0 ～7 的整数，即8 个状态，大于实际的状态数量7，在此采用边界吸收策略，即解码后的6 和7 位为相同控制状态。模糊量的语言值与解码值对应关系如表1 所示。

表1 模糊量的语言值与解码值对应关系

3.2 适应值函数

在研究中，适应值函数用于评测个体（模糊控制表）的优劣，是遗传算法执行“优胜劣汰，适者生存”的基本准则。在温度控制中应尽量减少调节时间，因此，定义如式（3）的适应值函数，适应值函数示意图如图2 所示。

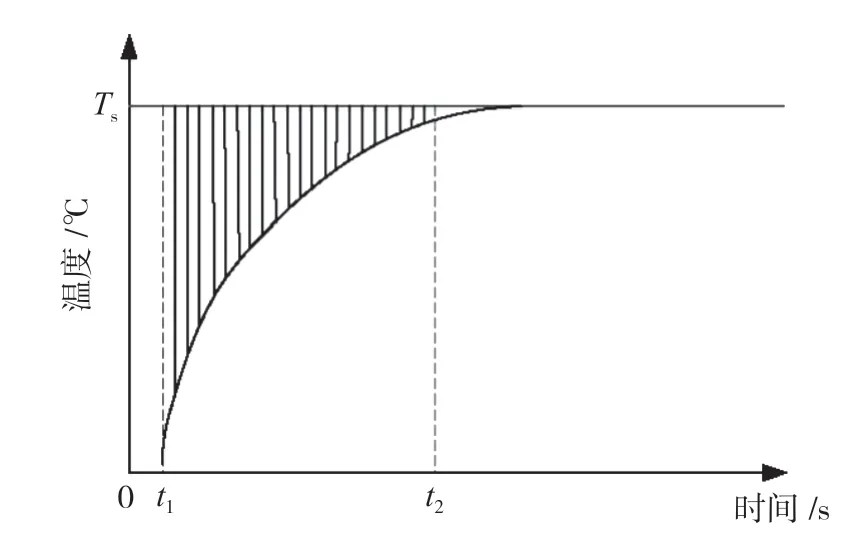
图2 适应值函数示意图

式中：f(x)——图2 中阴影区域的面积；

t1——温度开始变化的起始时间；

t2——液体温度与设定温度之差小于ε时的时间；

TS——恒温水浴设定的温度；

T(x)——温度变化曲线

根据图2 所示，如果温度控制时间越短，阴影部分的面积就越小，对应个体（模糊控制表）的温度控制效果就越好。根据上述的编码机制和适应值函数，就是在147 维空间中寻找满足上述适应值函数最小值所对应的模糊控制规则。

4 模糊PID控制在恒温水浴中的实现

设计的模糊PID 控制器是指当系统在初始启动阶段，温度偏差为液体的当前温度减去设定值，偏差变化率为零，此时采用模糊控制器；当进入稳态阶段时，设温度偏差的绝对值小于ΔT时，偏差和偏差变化率都较小，此时采用PID 控制器。采用这种控制模式能够克服传统PID 控制器在响应快速和超调上必须采取折衷的做法，使系统响应具有快速性和稳定性的特点。

为了提高系统响应的速度，用查表的方式实现恒温水浴温度的模糊控制。先将得到的模糊控制查询表以DB 数据块方式存入PLC 的内存中，然后通过存储器间接寻址的方法访问DB 块中所存储的模糊控制查询表中的数据。

5 仿真对比分析

5.1 遗传算法的收敛性分析

利用MATLAB 进行仿真实验，遗传算法的种群数量为20，迭代次数为30 次，个体交叉和变异概率分别为0.8 和0.05。每代最优个体的适应值函数值如图3 所示（适应值采用最大值归一化）。

图3 最优个体适应值变化曲线

通过上述过程可以看出，最优个体的适应值在第27 代后将不再发生改变，即进化过程在27 代收敛为局部最优解，所以设置最大迭代次数为30。需要注意的是，并不是所有进化过程都会在27 代后收敛于最优个体，但大部分情况如此，所以最大迭代次数在本研究中是经验值。

5.2 不同策略的温度控制系统变化曲线

为了进一步验证采用遗传算法优化后模糊控制规则表的模糊PID 控制优于传统的PID 控制和模糊PID 温度控制，进行了3 组仿真实验：传统PID 控制、模糊PID 控制、利用本文算法优化后的最优模糊控制规则表的模糊PID 控制。设水浴液体的初始温度为10 ℃，水浴设定的目标温度为20 ℃，ΔT为0.5 ℃。3 组仿真的温度控制曲线如图4 所示。

图4 3 种策略的控制曲线

根据图4 所示结果，基于GA 的模糊PID 控制系统的峰值时间约为570 s，模糊PID 控制小于600 s，传统PID 控制约为600 s。基于GA 的模糊PID 控制的超调量为0，模糊PID 控制的超调量小于传统PID控制。由此看出基于遗传算法优化的模糊PID 控制在3 种控制方式中的峰值时间最短，超调量最小，而且响应速度也比较快。

通过对比分析得出采用遗传算法优化模糊控制规则后的模糊PID 控制器得到了较高的控制准确度，明显提升了系统的整体控制效果，是一种有效的控制策略，在恒温水浴的温度控制系统中有较强的可行性，能够有效地改善系统性能。

6 结语

针对目前模糊PID 控制在恒温水浴温度控制过程中存在依赖专家经验等缺点，提出一种基于遗传算法模糊控制规则表的优化方法。该方法对模糊控制器的输出状态进行编码，以系统的调节时间构造适应值函数，通过遗传迭代求解最优的模糊控制规则表。仿真结果表明，该基于遗传算法优化后的温度控制系统可以获得快速、稳定、超调量小的控制效果，全面改善系统的动静态性能，满足控制要求。