纬编针织机编织过程中三角振动响应特性

戴 宁, 梁汇江, 胡旭东, 陆哲昊, 徐开心, 袁嫣红, 屠佳佳, 曾志发

(1.浙江理工大学 浙江省现代纺织装备技术重点实验室, 浙江 杭州 310018; 2.浙江理工大学 纺织科学与工程学院(国际丝绸学院), 浙江 杭州 310018; 3.浙江康立自控科技有限公司,浙江 绍兴 312500; 4.浙江恒强科技股份有限公司, 浙江 杭州 310018)

纬编针织机是一种在织针与三角的相互作用下,完成退圈、垫纱、弯纱、成圈等工艺的专用纺织设备[1]。如何提高纬编针织机运行状态的自感知、故障的自诊断能力是行业内研究的重点。近年来,有关纬编针织机状态及故障检测相关的研究也在逐步展开,覃善霖等[2-3]以电磁式选针器为研究对象,分别通过检测电磁线圈通断过程中电流的变化及刀头摆动规律,实现了电磁式选针器短路、断路及刀头异常故障的自诊断;Ma等[4]基于逆压电效用实现了压电式选针器选针过程中驱动梁的正反摆动;更进一步地,Peng等[5]基于压电陶瓷摆动过程的压电效应,在压电式选针器驱动梁摆动过程的同时实现了其位置的自检测;李军等[6]利用频闪原理,设计了选针器频率检测系统,实现了对选针器刀头故障的有效检测。以上研究是从选针器(电磁式、压电陶瓷式)状态的实时检测层面展开的,在一定程度上提高了选针机构运行状态的自感知、故障的自诊断能力。

戴昱昊等[7]、Heravi等[8]通过红外感光原理,设计并开发了各自的红外光电监测系统,分别实现了纱线状态的在线检测以及纬编针织机喂纱过程中纱线波动幅度的变化规律。此外,Li等[9-10]引入故障树分析法以及统计学规律法,提高了纬编针织机纱线张力大波动、断纱、走纱等故障诊断的准确率。以上研究是从纱线检测执行器状态的实时检测层面展开的,在一定程度上提高了送纱机构的自感知、故障的自诊断能力。在纬编针织机其它关键机构的自感知、故障自诊断能力提高的相关研究上,胡旭东等[11]将密度电动机的检测装置集成于一块电路板上,实现了密度电机位置的在线检测。

上述研究虽然从一定程度上提高了纬编针织设备自感知、故障自诊断的能力,但是其研究主要针对单一品种的执行器(选针执行器、纱线检测执行器、密度调节执行器等),通用性较差。当执行器的种类参数发生改变(如纬编针织机选用压电式选针器替换电磁式选针器或者纱线及织物品种改变)时,检测方式需要重新研究、调试,且即使各个执行器检测结果均正常,也无法保证纬编针织机的终端控制环节——出针方式准确,故从单一执行器的层面提高纬编针织机性能往往具有很大的局限性。纬编针织机编织的过程,实际上是织针撞击三角并沿三角轨道面作受迫升降运动的过程[12]。张华等[13-14]通过对纬编针织机编织过程进行动力学建模发现,织针针踵在撞击三角瞬时会产生振动,故由此可得,撞击过程三角同样会产生振动,且振动频率与针筒转速、出针方式相关。

本文结合纬编针织机编织过程中织针与三角间的受迫运动特性,设计编织过程三角振动响应特性测试平台,将压电陶瓷(PZT)贴于压电三角表面,形成“三角+PZT”耦合体,得到耦合体在不同转速、不同针法下的振动特性曲线,所得编织过程中三角的振动特性(振幅、频率)与转速、出针方式的数学关系对从振动层面实现纬编针织设备编织过程中工作状态及故障的实时检测具有一定借鉴意义。

1 工艺分析

织针的走针轨迹主要由选针器刀头动作及三角工作状态确定,进而形成各种纬编组织织物,织针内嵌于针筒左右两侧壁内,随针筒做圆周运动。在选针器刀片及三角的共同作用下,织针在织物编织过程中主要走埋针及出针2种轨迹。在出针轨迹下,织针未撞击到三角前以速度V1水平运动,撞击三角后以速度V2继续沿斜面运动,并引起三角沿各个方向的衰减振动,如图1所示,故不同的出针方式及针筒转速将影响三角的振动响应特性。

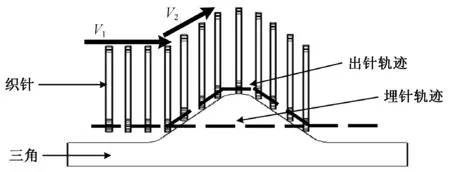
图1 编织过程织针沿三角受迫运动简图Fig.1 Diagram of forced movement of knitting needles along cam during knitting process

2 平台搭建

编织过程中,在针筒的带动下,参与编织的织针不断撞击工作三角引起其表面应激振动,其振动基频与织针撞击的频率一致,选用绍兴某纺织装备生产车间型号为RFSM20无缝内衣机为研究本体,将PZT粘贴于三角表面,形成“三角+PZT”耦合体对织针撞击频率进行捕获。由纬编针织机编织工艺可知,与织针发生撞击作用的三角主要有集圈三角、退圈三角、降针三角、成圈三角等,这4类三角与织针撞击作用本质上一致。为方便在研究本体上安装PZT传感器以及获取较强的振动信号,将PZT安装于退圈、中间针三角组件中,靠近降针三角位置,进而对织针撞击频率进行分析。图2示出“三角+PZT”耦合体的整体示意图、局部示意图、实物图。

图2 “三角+PZT”耦合体结构示意图Fig.2 Schematic diagram of "cam + PZT" coupling structure.(a) Overall schematic; (b) Partial schematic; (c) Physical map

由图2可知,PZT矩形薄片通过粘胶薄层贴附于降针三角上表面,导线1、2通过焊点1、2分别焊接于PZT矩形薄片上表面及降针三角上表面,织针沿退圈三角上升至退圈高度后,撞击降针三角下表面,并沿其下表面相对针槽做竖直下降动作。织针撞击降针三角瞬间产生冲击波,冲击波沿各个方向传播,使“三角+PZT”耦合体产生垂直于表面的应激振动,由于PZT矩形薄片的压电效应,可将此时织针与三角的撞击信号转换为同频率的电信号[15]。

3 三角振动响应特性

将图2中所示的导线1、2接入高性能示波器中,所研究对象RFSM20无缝内衣机正常编织最高转速为80 r/min,故在0～80 r/min的转速范围内,以10 r/min的时间间隔进行采样,不同转速下织针撞击“三角+PZT”耦合体时的振动电信号如图3所示。

图3 不同转速下织针撞击“三角+PZT”耦合体瞬时振动电信号特性Fig.3 Electrical signal characteristics of instantaneous vibration of knitting needle impacting "cam + PZT" coupling body at different speeds

对比图3(a)～(h)可知,织针撞击三角瞬间,振动电信号幅值在较短时间达到最大值,随后逐渐衰减到0,且衰减时间周期基本一致,均在200 μs左右,与撞击速度无关。纬编针织机的织针撞击三角的频率与针筒转速及出针方式有关,其中,在针筒转速为80 r/min,全出针模式下撞击频率最大,以RFSM20无缝内衣机(针数为1 152)机型为例,此时其撞击频率为1 536 Hz,即当前针位2次因撞击产生的振动时间间隔至少需要约651 ms,振动电信号持续时间远小于最高撞击时间间隔,相比选针器周期更可忽略不计,故理论上不同转速、不同针法下对应的振动电信号满足现有纬编针织机的实时性和灵敏性要求。

当织针针筒转速按10 r/min阶梯递增时,图3中所示曲线的振幅值逐渐递增,由两刚体碰撞理论可知,撞击瞬时,织针与三角间的冲击力与速度成正比,故当转速增加时,冲击力也逐渐增大,最终导致“三角+PZT”耦合体瞬时振动电信号最大幅值增大。

纬编针织机的织针随针筒作圆周运动,其链条及花型动作按针位进行控制,当织针速度稳定时,每枚织针在各时刻的针位确定,本文实验设置1×1、1×2、 1×3、2×2、平针等常见针织针法。在平针针法下,对“三角+PZT”耦合体瞬时的振动电信号进行测量,其结果如图4所示。图中浅色矩形波信号为当前路选针控制信号,其频率大于或等于1个针位移动时间的倒数且只与无缝内衣机总针数及针筒转速相关,蓝色线为“三角+PZT”耦合体瞬时的振动信号。对比图4(a)～(h)可知,“三角+PZT”耦合体检测到的振动频率及振动幅值与针筒转速成正相关,其大小与选针频率相等。

图4 平针针法时“三角+PZT”瞬时振动电信号特性Fig.4 "cam + PZT" instantaneous vibration electrical signal characteristics with flat needle method

当纬编针织机设置1×1针法、1×2针法、1×3针法、2×2针法时,“三角+PZT”耦合体瞬时振动电信号测量结果如图5～8所示。

图5 1×1针法时“三角+PZT”瞬时振动电信号特性Fig.5 "cam+PZT" instantaneous vibration electrical signal characteristics with 1×1 stitching method

图5～8所示橙、蓝曲线的定义与图4中橙、蓝曲线的定义一致,研究本体所用选针器为16段选针器。当纬编针织机做1×1针法时,当前路选针器选针数据为0b1010101010101010;当其做1×2针法时,当前路选针器选针数据为0b1001001001001001;当其做1×3针法时,当前路选针器选针数据为0b1000100010001000;当其做2×2针法时,当前路选针器选针数据为0b1100110011001100;当前路选针器选针数据中,二进制“1”代表选针器对应刀头向上摆动,对应织针出针,此时织针撞击三角,“三角+PZT”耦合体可检测到振动信号;二进制“0”代表选针器对应刀头向下摆动,对应织针埋针,此时织针针踵埋入针槽,“三角+PZT”耦合体无法检测到振动信号。故当做1×1针法(见图5)时,选针频率是“三角+PZT”耦合体检测所得振动频率的2倍;当做1×2针法(见图6) 时,选针频率是“三角+PZT”耦合体检测所得振动频率的3倍;当做1×3针法(见图7)时,选针频率是“三角+PZT”耦合体检测所得振动频率的4倍;当做2×2针法(见图8)时,选针频率是“三角+PZT”耦合体检测所得振动频率的4倍。对比图4～8中橙、蓝2条曲线可知,纬编针织机出针方式确定后,选针频率与振动频率的比值关系一定,如下式所示:

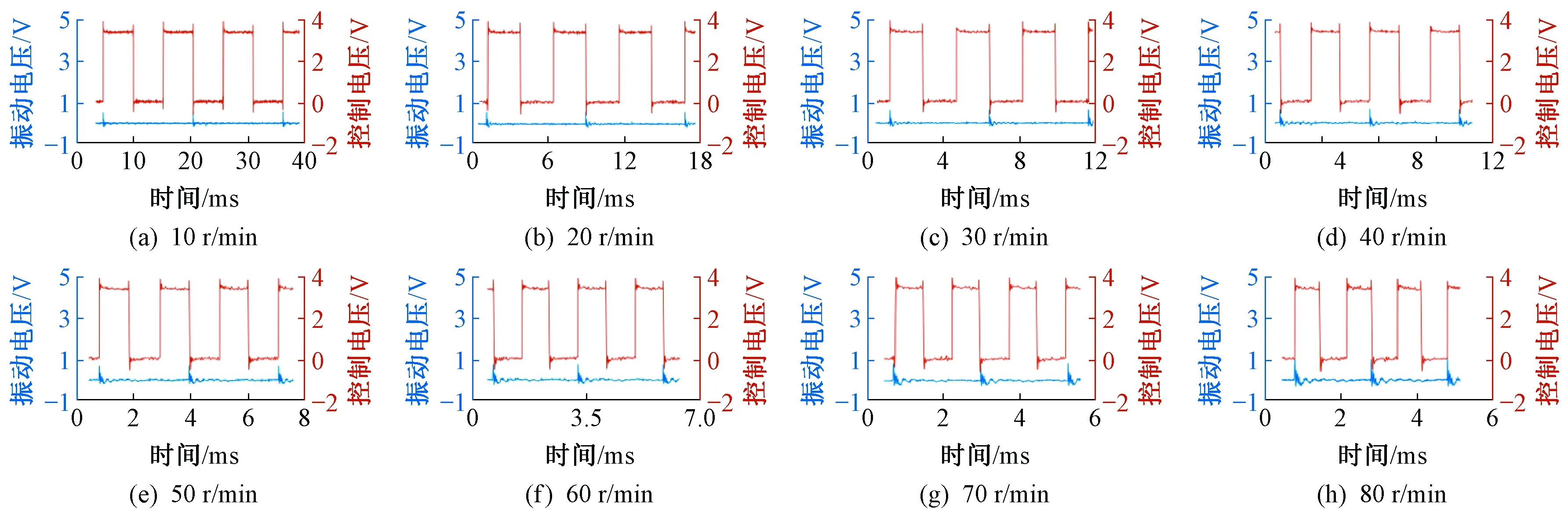
图6 1×2针法时“三角+PZT”瞬时振动电信号特性Fig.6 "cam+PZT" instantaneous vibration electrical signal characteristics with 1×2 stitching method

图7 1×3针法时“三角+PZT”瞬时振动电信号特性Fig.7 "cam+PZT" instantaneous vibration electrical signal characteristics with 1×3 stitching method

图8 2×2针法时“三角+PZT”瞬时振动电信号特性特性Fig.8 "Cam+PZT" instantaneous vibration electrical signal characteristics with 2×2 stitching method

式中:f为在出针方式为n时,耦合体检测所得振动频率,Hz;F为选针频率,Hz;n1,n2为出针方式的组合整数变量。

可见:当n2=0时,代表全出针,此时选针频率与“三角+PZT”耦合体检测所得振动频率相等;反之,当织针做n1×n2针法时,选针频率是“三角+PZT” 耦合体检测所得振动频率的(n1+n2)倍。利用这一规律结合纬编织针机花型工艺,可实现特定出针方式下的提花编织故障诊断。同理,对图4～8中相同转速下的振动曲线幅值最大值取平均值,并绘制其在不同针法下与针筒转速的关系曲线,如图9所示。可以看出:不同针法下,振幅最大值与针筒转速曲线几乎重合;且随针筒转速的增大而增大,其振动幅值仅与当前时刻针筒转速有关,而与具体针法无关。

图9 振幅-转速曲线Fig.9 Amplitude-speed curve

对图4～8中所测不同转速下的振幅最大值进行拟合,结果如图10所示。

图10 振幅拟合曲线Fig.10 Amplitude fitting curve

由图10可知,当纬编针织机的针筒转速在0～80 r/min的范围内增加时,“三角+PZT”耦合体检测所得振动信号最大值呈线性递增。这表明当针筒转速增加时,织针撞击在三角上的力增加,可利用振动信号最大值与振动转速的规律曲线,从振动的层面对纬编针织机编织过程转速的迟滞性及稳定性进行在线检测。

4 结 论

纬编针织机作为纬编织物生产的专用设备,其编织过程中工作状态及故障的实时检测对提高其编织性能和稳定性具有重要意义。本文结合纬编针织机编织过程实际是织针沿三角轨道做受迫运动的通用工艺本质,搭建纬编针织机编织过程三角振动响应特性测试平台,得到“三角+压电陶瓷(PZT)”耦合体在不同转速、不同针法下其振动特性(振幅、频率)与转速、出针方式的数学关系,主要得到如下结论。

1)织针撞击三角瞬间,振动电信号幅值在较短时间(相比选针器周期可忽略不计)达到最大值,随后逐渐衰减到0,且其衰减时间周期基本一致,均在 200 μs 左右,与撞击速度无关,故理论上可根据“三角+PZT”耦合体的振动衰减特性,实现在5 kHz以内撞击频率下的故障检测。

2)纬编针织机全出针状态时,选针频率与“三角+PZT”耦合体检测所得振动频率相等;反之,当织针做n1×n2针法时,选针频率是“三角+PZT”耦合体检测所得振动频率的(n1+n2)倍,故利用这一规律结合纬编织针机花型工艺,可实现特定出针方式下的提花编织故障诊断。

3)不同针法下,“三角+PZT”耦合体检测所得振动信号最大值随针筒转速线性递增,而与具体针法无关,故可利用振动信号最大值与振动转速的规律曲线从振动的层面对纬编针织机编织过程转速的迟滞性及稳定性进行在线检测。