基于概率密度函数的织物染色侵入动力学分析

2023-12-05姜绍华梁帅童裴刘军张红娟王际平

纺织学报 2023年10期

姜绍华, 梁帅童, 裴刘军, 张红娟, 王际平

(1.上海工程技术大学纺织服装学院, 上海 201620; 2.上海市纺织化学清洁生产工程技术研究中心, 上海 201620)

流体的动压、界面效应和织物结构显著影响织物的染色过程[1]。织物内部在任意时间和空间上的染料浓度的预测,是科学研究和实际生产中不可缺少的关键技术。此外,非水介质染色相关理论、工艺和配套技术发展迅速[2-4];但很多织物内部的染料浓度分析和评估仅取决于初始和最终状态,且缺少必要的相界面信息,而相界面信息对于诸多非水介质染色体系至关重要,因此有必要开发一个包含织物结构信息和界面效应的模型来预测织物中的染料浓度。

织物的染色过程通常是染料与织物材料之间的物理、化学作用随时间变化的连续过程,因此织物中的染料浓度是时间和位置的函数[5]。此外,织物在染色过程中自身的结构对其物理性质如密度、孔隙结构等有着较大影响,进而影响纤维与染液的液-固界面特性,如黏度、表面张力等,这些性质在织物内部流动和物质转移过程中都起着至关重要的作用[6-7]。以棉织物染色过程中的染料转移过程为例,染料分子溶于水中,经过水的流动与织物纤维接触,染液在纤维表面形成扩散边界层,进而染料分子通过扩散边界层向纤维内部扩散[8]。

由于织物中纤维间孔隙尺度约为10-6m,因此纤维与染液之间的相互作用主要由毛细作用力主导[9],毛细作用广义上是指固体与流体之间的界面相互作用产生于液体内部的凝聚,所以纤维间的染液流动以哈根-泊肃叶定律描述的毛细管效应为主[9]。随着X射线显微层析成像技术的发展,三维成像技术[10-11]已成为研究多孔介质中孔隙尺度过程的方法。应用先进的后处理程序和同步加速器显微成像技术,研究人员可实时成像甚至慢速观察流动过程,并从孔隙空间的界面提取相关的材料参数[12-13],如接触角等。与其它天然多孔介质不同的是,纤维仅依靠摩擦形成了相对稳定的毛细管[14]。有研究人员使用纤维取向概率密度函数开发了基于毛细管假设的模型[15-16],结果表明:织物结构和毛细管流动半径影响流速;同时,毛细管流动半径取决于纤维半径和纤维体积分数。

本文研究的目标是构建织物内部一维毛细管流速v(x,t)和染料质量浓度c(x,t)预测模型。基于这些模型,以C.I.活性红195和棉织物为例,通过给出初始条件和边界条件来验证数值解,并讨论了纤维体积分数、接触角、表面张力和流体黏度的影响。

1 织物中的毛细管流动和浓度模型

基于纤维取向概率密度函数对织物的毛细管半径建立数学模型,从而推导出毛细管流动模型和浓度模型。x代表织物坐标,x=0和x=L分别代表织物的起点和终点。

哈根-泊肃叶(Hagen-Poiseuille)方程是一种经典的描述由压力驱动的毛细流动方程[17]:

(1)

式中:Q为体积流量, m3;t为时间, s;rc为平均毛细管流动半径,取值为4.14×10-6m[18];μ为流体黏度,取值为8.9×10-4Pa·s[15];x为流动距离, m;∑p为流动总压力,Pa,其计算公式为

∑p=pc+pd+pg

(2)

式中:pc为毛细管压力, Pa;pd为动压, Pa;pg为重力导致的静压, Pa。计算公式分别为:

(3)

(4)

pg=-xρg

(5)

将式(2)～(5)代入式(1)得到:

(6)

式中:γ为流体表面张力,取值为0.072 N/m[15];θ为接触角[15],取值为0.7 rad;ρ为流体密度,取值为997 kg/m3;u为流体初始流速, m/s;g为重力加速度,取值为9.8 m/s2。

(7)

根据Washburn和Trabi的结果,当u=0时,得到式(7)的解析解[9,17]:

(8)

式中,L为织物总长,取值为0.1 m。

染液沿着由织物纤维形成的毛细管在织物中流动,基于纤维取向概率密度函数[16]给出平均毛细管流动半径rc的计算公式:

(9)

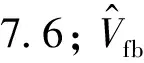
(10)

流体内的染料质量浓度c(x,t)[19]为

(11)

式中:φfab为织物孔隙率,取值为0.812 9;v为染液流速, m/s;c为染料质量浓度, g/L;D为质量扩散系数, m2/s;Sdep为染料在纤维上的沉积速率,g/(L·s)。

2 织物表征和模型参数

2.1 织物表征

织物是纤维、空气、水分的复合材料,然而在实际计算中,空气和水分经常被忽略,一块织物仅视为干纤维的集合。孔隙率φfab是式(11)的核心参数之一,它可用复杂的仪器测量,也可通过下式计算得到:

(12)

织物比表面积(Assa, 1/m)为

(13)

式中:df为纤维直径[18], 取值为1.33×10-5m;lfb为纤维长度, 取值为0.01 m;N为纤维数量。

如前所述,纤维质量Mfb约等于织物质量Mfab,那么纤维数量为

N=Mfab/(ρfbVfb)

(14)

式中,Vfb为单根纤维体积, m3。

织物的厚度参照ISO 5840—1996《纺织品和纺织制品厚度的测定》,采用Y9141D型数字式织物测厚仪(宁波纺织仪器厂)测量。

2.2 扩散率和沉积率

流体中分子的质量扩散系数D由斯托克斯-爱因斯坦(Stokes-Einstein)方程[20]定义:

D=kbT/(6πμr)

(15)

式中:r为染料分子半径[21],取值为10-10m;kb为斯特藩-玻尔兹曼(Stefan-Boltzmann)常数,取值为5.67×10-8W/(m2·K4);T为流体温度,取值为313.15 K。

式(11)中的沉积速率Sdep可通过下式[22-23]估计:

Sdep=kφfabc

(16)

式中,k为沉积速率系数, 1/s,其计算公式为

k=ceEAssau。

式中:ce为纤维表面系数,取值为0.1[24];E为保留系数,取值为0.01[24]。

2.3 实验验证

使用YG87型毛效测试仪(宁波纺织仪器厂)进行实验验证。将宽度为2 cm的干燥纯棉织物试样垂直悬挂在毛效测试仪上,然后以极缓慢速度使试样下降以达到准静态过程,使式(7)和(10)中的u≈0。毛效测试仪中装有0.03 g/L的活性红195溶液,其温度维持在40 ℃。测试环境温度为21 ℃,相对湿度为60%。本文研究使用了由Testmaterials B.V.测试中心生产的CN42标准白色棉织物。活性红195染料由上海Adamas-Beta试剂有限公司提供。使用相机记录了15 min的毛细流动过程,然后使用Datacolor 800分光测色仪(美国Datacolor公司)对样品颜色进行了测量和比较。纯棉织物样品均使用了FOM 71 CLS滚筒洗衣机(瑞典伊莱克斯公司),采用ISO 5A洗涤程序进行3次预洗以避免内应力和杂质的影响,并放置在恒温恒湿箱内在相对湿度为60%,温度为25 ℃的条件下干燥、平衡备用。

2.4 边界条件、初始条件和数值求解

在t=0时织物任何位置的毛细管流速v和染料质量浓度c均等于0,即v(x,0)=0,c(x,0)=0。入口处的初始质量浓度c(0,0)为0.03 g/L。计算时间间隔为0～900 s,即15 min。速度v(x,t)直接由式(10) 定义,同时Fries给出了u=0的解析解[22-25]。使用COMSOL 5.5 提供的一般形式边界偏微分方程求解器求解式(11)的数值解[26]。

3 结果与讨论

3.1 预测和实验结果的比较

使用分光测色仪测量t=900 s时样品织物的K/S值以表征染料质量浓度,对数据进行归一化处理来消除颜色和质量浓度单位的差异。表1列出不同时刻织物中染液流动距离的模型预测值与实验测得值及相对误差。图1示出预测值与实验结果的流速和质量浓度对比。

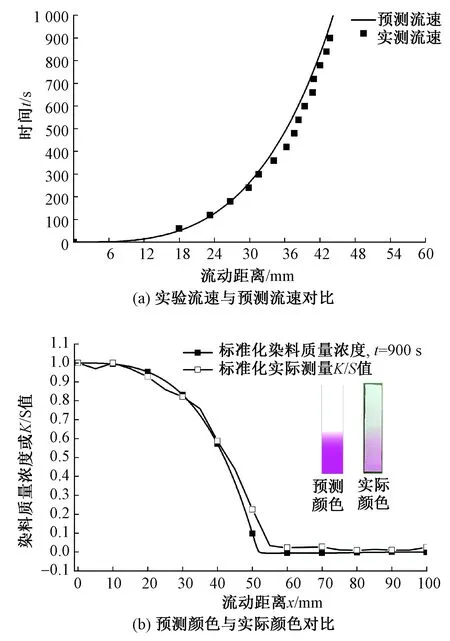
图1 预测值与实验结果对比Fig.1 Comparison of predicted values and experimental results.(a) Flow rate comparison between predicted and experimental measurements; (b) Concentration comparison between predicted and experimental measurements

表1 模型误差Tab.1 Model prediction error

由表1可知,数值模型预测值与实验结果的误差均在4%以内,模型精度较高,可较好地模拟不同时刻织物内染液的流动距离。从图1可看出,实验测得流动距离与模型计算所得流动距离的变化趋势相同,误差较小,在质量浓度预测方面,预测颜色与实际颜色变化趋势相同,误差较小。

3.2 织物中活性红195质量浓度

图2示出当t=10,60,120,300,900 s时活性红195在x=0～L范围的质量浓度分布。可以看出,质量浓度c随着时间的增加而增加。在较早的阶段,例如在t=10～120 s时,质量浓度分布c(x,t)比300 s和900 s更陡峭,意味着此时染色部分与未染色部分的分界线更为明晰。

图2 不同时刻下织物不同位置的染料质量浓度分布Fig.2 Concentration distribution at different position under different moments

3.3 纤维体积分数的影响

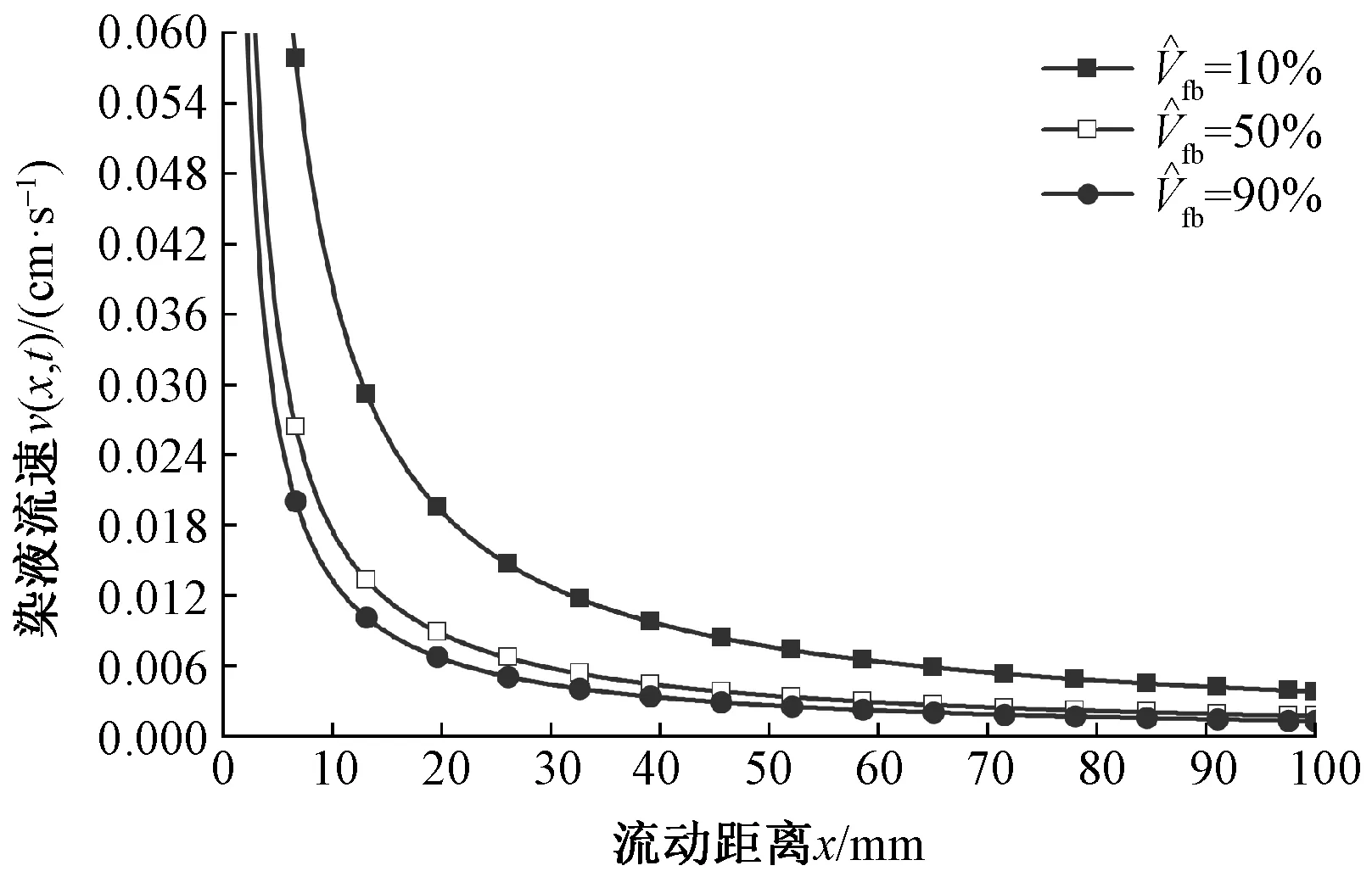
图3 纤维体积分数对v(x,t)的影响Fig.3 Effect of fiber volume fraction on v(x,t)

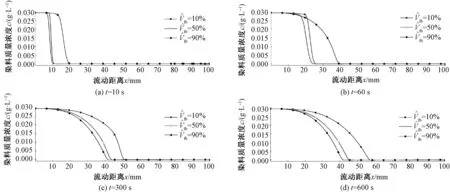
图4 纤维体积分数对c(x,t)的影响Fig.4 Effect of fiber volume fraction on c(x,t)

3.4 接触角θ的影响

图5、6分别示出接触角θ对流速v(x,t)和质量浓度c(x,t)的影响。其中θf值为0.7 rad。对于v(x,t),随着θ的增加,织物内部的染液流速逐渐减小。当θ>π/2时,界面将形成向上凸出的液面。在这种情况下,不会发生渗吸过程,如θ=2.5θf结果所示。此外,在流动的初始阶段,即当t=10 s和60 s时,在不同的x位置,接触角越大,质量浓度c(x,t)越低。

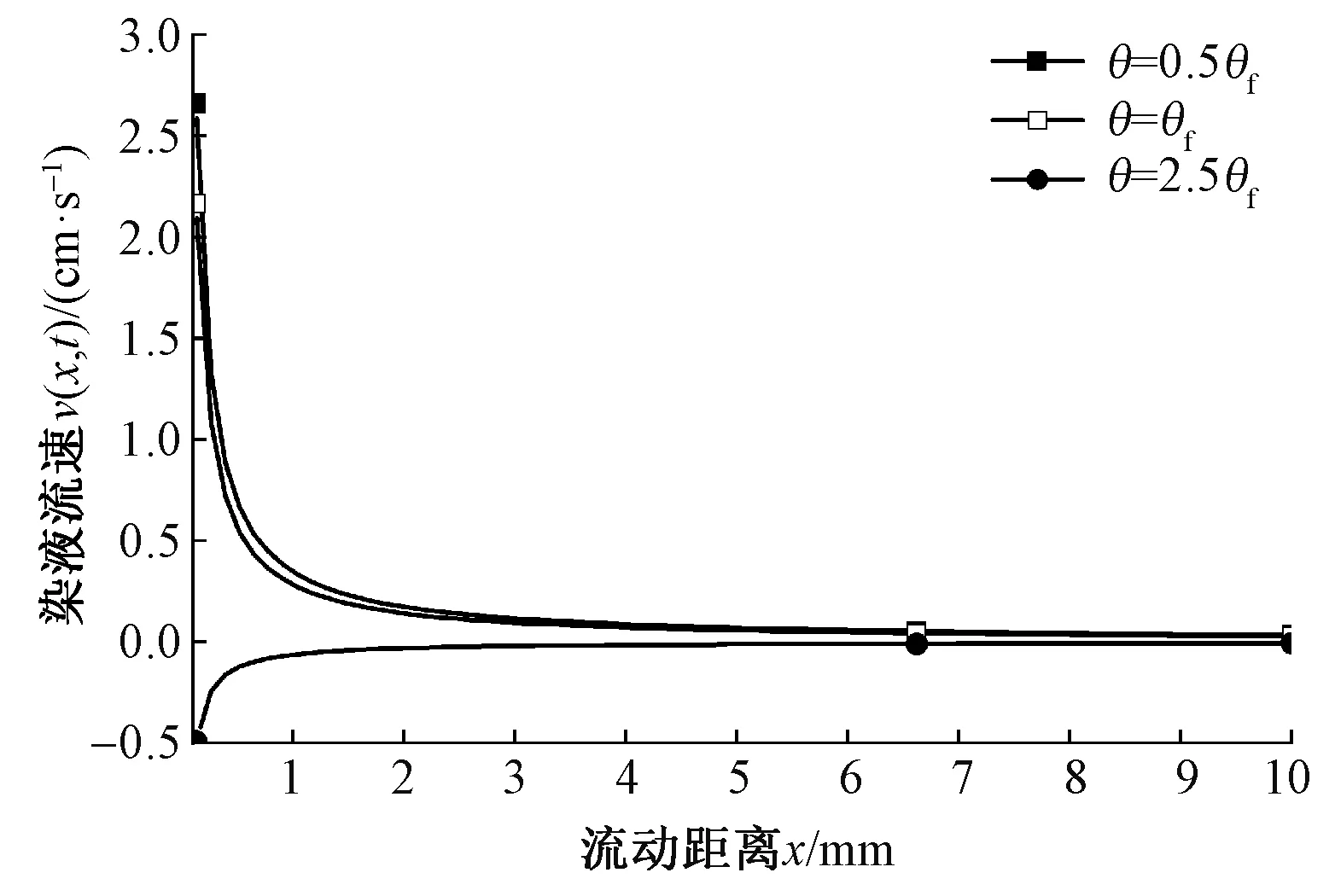
图5 接触角θ对v(x,t)的影响Fig.5 Effect of contact angle θ on v(x,t)

图6 接触角θ对c(x,t)的影响Fig.6 Effect of contact angle θ on c(x,t)

3.5 表面张力γ的影响

本文研究比较了不同表面张力0.5γf、γf和2γf的计算结果。其中γf取值为0.072 N/m。图7、8分别示出流体的表面张力对织物中染液流速和染料质量浓度的影响。可以看出,随着表面张力的增加,织物中的染液流速增加。在流动的初始阶段t=10 s 和60 s时,较大的表面张力会导致更高的质量浓度。到了t=300 s,0.5γf所对应的质量浓度逐渐超过了γf的计算结果。在最后t=600 s时,0.5γf对应的质量浓度已经完全超过γf。

图7 表面张力γ对v(x,t)的影响Fig.7 Effect of surface tension γ on v(x,t)

图8 表面张力γ对c(x,t)的影响Fig.8 Effect of surface tension γ on c(x,t)

3.6 黏度μ的影响

图9、10分别示出黏度μ对质量浓度c(x,t)和流速v(x,t)的影响。可以看出,随着黏度μ的增加,织物中的染料流速逐渐降低。在织物空间x∈(0,L)中,黏度μ越大,织物中的染液质量浓度越低。就时间t而言,当黏度较低时,织物中的染料质量浓度c(x,t)上升得更快。当流体黏度较大(μ=10μf)时,织物内的染液流速较慢,进而导致织物中的染料扩散也比较缓慢。