基于灰色系统理论的筒子纱卷绕密度测量误差预测

2023-12-05周其洪韩伟龙岑均豪

纺织学报 2023年10期

周其洪, 韩伟龙, 陈鹏, 洪巍, 岑均豪

(1.东华大学纺织装备教育部工程研究中心, 上海 201620; 2.东华大学机械工程学院, 上海 201620;3.广州盛原成自动化科技有限公司, 广东广州 511400)

筒子纱卷绕密度是影响筒子纱染色质量的关键因素[1]。当筒子纱卷绕密度过小时,纱线太松,容易重叠且相互纠缠,成形不好难以染色[2];当筒子纱卷绕密度过大时,染液流体对筒子纱的渗透性较差,染色后的筒子纱内外色差较大[3]。因此,提升筒子纱卷绕密度的测量精度具有重要应用价值。

目前筒子纱卷绕密度的测量主要采用人工法和仪器法。人工法主要是使用游标卡尺等测量工具手动测量筒子纱的外形参数,运用数学公式和筒子纱的质量计算卷绕密度[4]。该方法存在测量精度差,效率低等问题。仪器法包括接触式仪器法和非接触式仪器法。接触式仪器法主要是将硬度测试仪的探针插入到筒子纱内部,通过测量各层纱线的硬度来间接估测卷绕密度[5]。这种测量方法会对筒子纱的纱线结构造成一定的破坏,测量精度不高。非接触式仪器法主要有机器视觉法和激光扫描建模法。机器视觉法主要是利用工业相机获取筒子纱的侧面轮廓,通过图像分析计算筒子纱的体积,再配合纱线的质量计算筒子纱的卷绕密度[6]。该方法具有测量效率高和保持筒子纱纱线结构完整的优点,但当筒子纱表面轮廓存在凹凸不平的特征时,测量精度将会降低。激光扫描建模法主要是使用激光传感器采集筒子纱的外形轮廓和质量传感器采集纱线的质量,通过数据处理计算筒子纱的卷绕密度[7]。激光扫描建模具有测量效率高和测量精度稳定的优点,符合当下高质量生产的需求。在实际生产中,使用激光扫描建模的筒子纱卷绕密度测量方法其采样周期和步进电动机的脉冲频率要根据需求进行调整,导致无法直接了解新的采样周期和脉冲频率对测量精度的影响。为进一步提高该方法的测量精度,需通过分析测量参数与测量误差之间的关系,并采用合适的预测模型对测量误差进行预测。

考虑到测量参数和测量误差之间存在较大的复杂性和不确定性,可视为数据信息不全面的灰色系统。适合本研究的模型主要有灰色预测模型和BP神经网络预测模型。灰色系统理论是一种研究小数据、贫信息不确定性问题的方法[8],通过对部分已知的信息进行分析,推测出未知部分的信息。BP神经网络方法需要的数据量较大,计算量也更大[9],不是很适合本研究,因此,本文选择灰色系统模型对卷绕密度的测量误差进行预测。经典的灰色系统模型为GM(1,1),该模型主要针对单一变量进行分析[10];对于包含多因素变化的灰色系统需要建立GM(1,N)模型进行系统关联预测[11],以提高预测精度。多变量GM(1,N)模型在短期预测中表现出较强的预测精度[12-13],结合实际应用情景对模型做出相应修改以达到更优的预测效果。

本文利用灰色关联分析测量参数来满足灰色建模要求,结合实际建模参数间的非线性关系,提出使用经过背景值优化和分数阶累加生成优化的多变量GM(1,N)幂模型进行建模和预测,再引入粒子群算法优化求解幂模型的最优幂指数,得到拟合效果最佳的建模参数。在经典多变量GM(1,N)模型中引入幂指数使影响因子变量对主行为变量序列产生非线性的影响,使用线性结构的背景值优化方法使模型的拟合精度提高,使用分数阶累加生成优化使模型的预测精度得到进一步提高。

1 多变量灰色GM(1,N)幂模型

1.1 GM(1,N)幂模型的基本形式

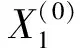
(1)

式中:a为系统发展系数;bi为驱动系数;λi为影响因子变量的幂指数。令:

(2)

(3)

1.2 GM(1,N)幂模型的缺点分析

在实际使用传统多变量灰色GM(1,N)幂模型建模和预测的过程中发现,该模型只针对理想条件下的数据预测精度高,并不具有普适性,存在如下 2方面不足。

为解决传统多变量GM(1,N)幂模型存在的缺陷,本研究在优化的GM(1,N)幂模型中引入线性结构优化的背景值来重新推导时间响应式,引入分数阶累加生成来解决区间预测缺少前置条件的问题,引入粒子群优化算法进行幂指数自适应寻优;并将基于粒子群优化算法求解优化GM(1,N)幂模型记为PSGM(1,N)幂模型。

2 多变量PSGM(1,N)幂模型优化

2.1 模型灰色关联度分析

灰色关联分析法是通过分析样本参数中蕴含的规律,用样本参数中规律的趋向度来评判参数间的关系度[14]。如果关系度值大于0.5,那么说明参数间具有较强的灰色关联性,适合用于灰色建模[15]。

以实际测量计算得到的卷绕密度测量误差数据为主行为变量序列x1=(x1(1),x1(2),…,x1(n)),影响测量误差的各个因素,如激光传感器的采样周期、步进电动机的脉冲频率等作为影响因子变量序列xi=(xi(1),xi(2),…,xi(n)),i=2,3,…,m。其中:m-1为影响因子变量的数量;n为主行为变量序列的数量。

Li(k)=

(4)

式中:k=1,2,…,n;i=2,3,…,m;ρ为灰关联系数的辨别值,取0.5。

利用计算得到的灰关联系数Li(k),通过式(5)获取灰色关联度值Ri。

(5)

式中,Ri代表影响因子变量序列xi对主行为变量序列x1的相关程度,值越大说明影响因子变量序列对主行为变量序列影响程度越大。通过灰色关联分析,判断采样周期、脉冲频率和参数K对卷绕密度测量误差的影响程度。

2.2 模型背景值优化

在实际应用过程中,影响因子变量序列的变化幅度存在较大的情况,如继续使用式(2)进行建模,将会大大降低预测精度。为解决这种情况带来的误差,使用式(6)的线性结构对传统的背景值生成方式进行优化。

(6)

式中,γ为待定系数。

将线性结构优化生成的背景值代入GM(1,N)幂模型式(1)中得:

(7)

对式(7)进行求解得到优化GM(1,N)幂模型的时间响应式:

(8)

2.3 模型分数阶累加生成优化

r阶整数累加算子式为

X(r)(k)=

(9)

式中,k=1,2,…,n。

为适应区间内预测,采取将r阶整数累加算子式优化为r阶分数累加算子式生成数据序列区间内的新序列。具体通过使用Gamma函数Γ(n)来实现:

(10)

2.4 幂模型参数优化

考虑到幂指数的取值与拟合结果之间没有确切的函数关系,将最小平均绝对相对误差作为评价模型拟合效果好坏的标准。通过这种方式,将求解模型最优参数转化为求解最优非线性优化模型,并在评价模型拟合效果的过程中计算出幂指数和灰参数。评价模型拟合效果的适应度函数核心式为

(11)

(12)

式中:t为迭代次数;w为惯性系数;c1和c2为加速系数;r1和r2为[0,1]区间内的2个随机数。

使用PSO算法进行最优幂指数求解,步骤如下。

步骤1 按粒子群规模初始化种群,明确优化目标为求解最优幂指数,用幂指数设定迭代条件,设定最大迭代次数M,并对所有粒子属性初始化。

步骤2 根据式(12)对每个粒子的速度和位置进行迭代更新。

步骤4 把每个粒子当前位置的适应度值与个体最优位置的适应度值进行比较,以此获取当前种群最优的适应度值。

步骤5 当达到循环终止条件时停止循环,并输出最优结果,否则转到步骤2继续迭代更新。

粒子群优化算法求解优化GM(1,N)幂模型具体求解流程图如图1所示。

图1 粒子群算法优化GM(1,N)幂模型Fig.1 Particle swarm optimization GM (1, N) power model

3 筒子纱卷绕密度测量误差预测

3.1 灰色建模前处理

在使用激光扫描建模测量筒子纱卷绕密度时,影响测量精度的因素包括2个数据采集装置上的外部参数和1个数据处理程序中的内部参数,分别为:激光传感器的采样周期、步进电动机的脉冲频率和重合点自动剔除算法中的累加参数K。激光传感器的采样周期和步进电动机的脉冲频率共同决定了采集到的筒子纱外部轮廓数据点的数量和点与点之间的距离,数据点的特征决定了筒子纱外部轮廓的拟合效果,直接影响到数据处理结果;重合点自动剔除算法中的累加参数K决定了数据降噪处理后噪声点的剔除效果,影响数学建模时卷绕密度的计算。

本文研究选取了3种不同密度规格的筒子纱:卷绕密度标准值为0.381 g/cm3的筒子纱A,卷绕密度标准值为0.411 g/cm3的筒子纱B和卷绕密度标准值为0.361 g/cm3的筒子纱C。在标准实验环境中分别采集了10组原始数据,如表1所示。将前7组数据作为建模数据,后3组数据作为预测数据。筒子纱A的平均直径为200 mm,质量为1 591 g,筒子纱中纱线平均高度为148 mm,筒管的质量为 128 g, 筒管的直径为66 mm;筒子纱B的平均直径为188 mm,质量为1 584 g,筒子纱中纱线平均高度为 157 mm, 筒管的质量为124 g,筒管的直径为 66 mm; 筒子纱C的平均直径为205 mm,质量为 1 590 g, 筒子纱中纱线平均高度为 148 mm, 筒管的质量为124 g,筒管的直径为66 mm。

表1 筒子纱卷绕密度测量误差及相关影响因素Tab.1 Measurement error and related influencing factors of bobbin winding density

为分析各影响因素和测量误差的相关性强弱,对建模数据进行灰色关联度分析,结果如表2所示。各影响因素都对测量误差存在着较强的相关性,灰色关联度值均大于0.5,满足灰色建模的前提条件,因此,选取脉冲频率、采样周期和参数K这3个因素研究测量误差具有合理性。

表2 灰色关联度值Tab.2 Gray associativity value

3.2 灰色预测模型建立

为对比分析,本文将分别建立经典多变量GM(1,N) 模型、传统多变量GM(1,N)幂模型和多变量PSGM(1,N)幂模型对3种不同规格筒子纱的卷绕密度测量误差进行预测,分析比较这3种模型的建模精度和预测精度。基于表1中的建模数据分别建立 3种灰色模型,通过对建模数据进行训练得出8～10组预测数据,与表1中后3组实测数据进行对比验证,得到3种模型的误差分析结果,如表3所示。

表3 3种多变量灰色模型对卷绕密度测量误差的模拟和预测结果Tab.3 Simulation and prediction results of winding density measurement error by three multivariable grey models

通过模型的定义,分别求解得到3种灰色预测模型的建模参数和时间响应函数。

1) 经典多变量GM(1,N)模型。

A:a=0.174 962,b2=-0.515 936,b3=0.503 788,b4=0.334 878。

B:a=0.262 218,b2=-0.318 934,b3=0.465 395,b4=0.241 033。

C:a=0.164 061,b2=-0.468 142,b3=0.462 881,b4=0.305 006。

2) 传统多变量GM(1,N)幂模型。

A:a=-0.240 608,b2=-10.227 26,b3=12.331 97,b4=-1.514 65,λ2=-0.952 416,λ3=-0.939 594,λ4=-2.471 19。

B:a=-0.234 294,b2=-11.667 2,b3=13.683 9,b4=-1.237 249,λ2=-0.824 079,λ3=-0.771 271,λ4=-0.852 936。

C:a=-0.240 562,b2=-24.651 02,b3=24.555 22,b4=0.436 428,λ2=-1.364 39,λ3=-1.404 708,λ4=-1.628 032。

3) 多变量PSGM(1,N)幂模型。

A:a=0.057 236,b2=-0.987 618,b3=0.325 170,b4=1.162 383,λ2=-7.181 310,λ3=3.113 668,λ4=0.053 126。

B:a=0.010 864,b2=-1.077 918,b3=1.548 953,b4=0.829 195,λ2=-0.999 157,λ3=1.209 710,λ4=1.571 737。

C:a=-0.018 98,b2=-0.815 084,b3=0.172 959,b4=1.244 397,λ2=-5.416 54,λ3=3.754 956,λ4=-0.041 565。

从表3可看出,在建模精度方面,筒子纱A、筒子纱B和筒子纱C的经典多变量GM(1,N)模型的平均相对误差分别为28.45%、23.06%和30.15%;使用传统多变量GM(1,N)幂模型得到的平均相对误差分别降为2.15%、2.49%和2.16%;使用经过粒子群算法优化后的多变量PSGM(1,N)幂模型的预测平均相对误差进一步降为2.05%、0.40%和0.74%,建模精度显著提高。

从表3还可看出,在模型预测方面,优化后的多变量PSGM(1,N)幂模型的预测精度明显高于另外2种模型。筒子纱A、筒子纱B和筒子纱C的多变量PSGM(1,N)幂模型的预测平均相对误差分别为2.78%、2.26%和2.44%,经典多变量GM(1,N)模型的预测平均相对误差分别为14.98%、6.94%和17.40%,传统多变量GM(1,N)幂模型的预测平均相对误差分别为5.28%、4.58%和4.70%。多变量PSGM(1,N)幂模型、经典多变量GM(1,N)模型和传统多变量GM(1,N)幂模型的预测平均误差分别为2.49%、13.11%和4.85%;相比于经典多变量GM(1,N)模型,多变量PSGM(1,N)幂模型和传统多变量GM(1,N)幂模型的预测精度分别提升了81.0%和48.6%。

综上所述,经过粒子群算法优化后的多变量PSGM(1,N)幂模型,在建模精度与预测精度方面都优于另外2种模型,表明优化后的模型具有更高的实际应用价值,更适合筒子纱卷绕密度测量误差的预测。

3.3 密度测量误差校正

为保证激光扫描建模的筒子纱卷绕密度测量方法在采样周期、脉冲频率和参数K改变后的测量精度,提出使用密度测量误差校正的方法提高密度测量的准确性。密度测量误差校正方法是在卷绕密度测量值y的基础上加上密度测量误差预测值e,得到校正后更精确的卷绕密度值y′。

采用多变量PSGM(1,N)幂模型分别对表1筒子纱A、B和C中数据序号为8、9、10的3组数据进行测量误差预测,求解得到的密度测量误差预测值分别为:筒子纱A,e8=0.039 179 g/cm3,e9=0.043 626 g/cm3,e10=0.048 827 g/cm3;筒子纱B,e8=0.043 367 g/cm3,e9=0.048 187 g/cm3,e10=0.054 181 g/cm3; 筒子纱C,e8=0.038 212 g/cm3,e9=0.042 981 g/cm3,e10=0.048 133 g/cm3。结合卷绕密度测量值y利用密度测量误差校正法,求解得到卷绕密度测量误差校正结果,如表4所示。表中精度提高率计算方法为:卷绕密度校正值与卷绕密度测量值的绝对误差除以卷绕密度精确值。