分布式螺旋桨倾转角度对机翼气动性能的影响*

廖逸枭， 郑敏， 章录兴， 余发源， 段焰辉

1.中山大学航空航天学院，广东 深圳 518107

2.中山大学系统科学与工程学院，广东 广州 510275

随着飞机制造商和航空公司越来越注重燃油效率、环境保护以及飞行可持续性，绿色航空这一概念越来越受到世界范围内研究者的重视。电推进飞机因碳排放少、噪声低等优点获得广泛研究，成为未来飞行器的重要发展方向之一。分布式电推进构型在气动和推进效率的额外增益，使得该构型具有更大的发展潜力。

近年来，分布式电推进技术得到广泛研究，相关概念也被陆续提出（孔祥浩等，2018）。美国国家航空航天局（NASA）发布的X-57 验证机在机翼前缘安装分布式高升力螺旋桨，在起降阶段通过滑流作用大幅提高机翼升力，显著改善了机翼的低速特性（Stoll et al.，2014）。

在对分布式电推进飞行器的气动设计以及优化过程中，Viken et al.（2017）发展出一种较优翼型提高了分布式前缘动力飞机在巡航时的气动特性。Litherland et al.（2017）设计了一种可折叠的分布式螺旋桨，在飞行器巡航时折叠螺旋桨桨叶减小了巡航阻力。Deere et al.（2017）研究了分布式螺旋桨旋转方向组合对升力系数的影响，结果显示相同旋转方向且与翼尖涡流旋转方向相反的分布式螺旋桨能显著增加升力系数。Fei et al.（2018）研究了螺旋桨桨盘相对机翼的几何位置对机翼的气动特性的影响。Litherland et al.（2021）对分布式螺旋桨飞机进行了一系列的风洞实验测试，测试结果显示，螺旋桨桨叶在动态折叠过程中能平稳运行。

Takallu et al.（1992）研究了螺旋桨滑流对带前缘缝翼和克鲁格襟翼的多段翼的影响，测试了螺旋桨在垂直、水平位置的变化和相对机翼的倾转对机翼的气动影响，风洞实验结果显示螺旋桨倾转提高机翼升力系数的效果最好。分布式电推进飞行器主要通过前缘升力螺旋桨产生的滑流提高机翼在起降阶段的升力系数，因此，研究螺旋桨倾转对分布式电推进飞行器在起降阶段时的气动特性的影响有较大意义。在对螺旋桨桨盘倾转的气动特性研究中，对分布在机翼前缘的螺旋桨产生的滑流流场计算是全机气动数值模拟的重点。

对此，国内外学者做了大量对螺旋桨滑流的数值模拟工作。Whitfield et al.（1983）将螺旋桨简化为一个作用盘面模拟滑流效应，数值结果与实验结果对比较好。Conway （1998）提出一个准确的隐式方法用以求解作用盘周围流场。Strash et al.（1998）提出基于动量-叶素理论的作用盘模型用以研究螺旋桨滑流效应，数值计算结果与风洞实验数据结果匹配。近年来，随着CFD 理论的日渐完善，N-S 方程逐渐应用到螺旋桨的数值计算中。Veldhuis et al.（2000）基于N-S 方程，分别采用作用盘方法和完整桨叶模型下的准定常方法，对SR-3先进桨扇/短舱模型进行计算，两种方法的计算结果和风洞实验结果相近。李博等（2008）推导了螺旋桨等效盘模型的相关气动计算公式，建立了考虑多因素的较通用的等效盘模型，使用该模型进行三维流场计算，与真实实验数据结果吻合较好。杨小川等（2014）基于非定常Euler 方程，综合动态拼接结构网格技术和双时间步推进方法，通过对某单独螺旋桨的计算，验证了该方法的可行性。

对于涉及计算螺旋桨滑流对下游机翼的作用时，尽管完整桨叶模型方法能够提供更多的流场细节，但是需要建立具体的桨叶模型并划分网格，效率较低。作用盘/等效盘模型具有计算速度快，求解简便的优点，在只关注定常解的前提下进行快速评估非常有效，因此，本文在确保计算准确的前提下，使用作用盘/等效盘模型作为螺旋桨数值模拟的基础方法对分布式螺旋桨进行数值模拟，并与实验结果比对。在X-57 验证机型迭代过程中的某款构型的基础上，分别对起飞和降落构型下的滑流效应进行分析。分析了螺旋桨倾转角对机翼的有效升力系数的影响，计算了起飞或者降落阶段相对更优倾转角。

1 数值模拟方法

1.1 控制方程

流场中直角坐标系下微分形式的三维N-S 方程为

其中Q为守恒变量矢量，E，F，G为对流通量矢量，Ev，Fv，Gv为黏性通量项，J为源项，计算式如下

以上各式中，ρ，u，v，w，p，e和h分别表示气体密度、速度矢量在x，y，z坐标方向上的分量、压力、单位质量的总能和总焓。fx，fy，fz为体积力在直角坐标系下的各分量，在不涉及等效盘的边界计算时一般为零。

对流场的计算基于雷诺平均N-S方程，为了能够较为准确地模拟在气动分离等复杂流动，湍流模型采用SST（shear stress transfer）k-ω模型，该湍流模型对大迎角下高升力复杂外形流场模拟性能较好（Tang et al.，2016）。

本文主要研究螺旋桨滑流影响下的机翼起降构型气动特性，机翼和螺旋桨轮毂附近马赫数较低，流动为不可压缩流；螺旋桨桨尖附近处于跨声速状态，流动为可压缩流。在低马赫数下，基于密度的方法求解可压缩流动方程容易出现计算不收敛的情况，因此，本文采用低速预处理方法来进行流场数值模拟，以提高低速状态下计算的收敛性。

1.2 等效盘数学模型

本文采用的等效盘模型将螺旋桨桨叶旋转运动所扫过的区域假想为一个没有厚度的圆盘，该圆盘前后气流与螺旋桨前后气流参数相同，从等效盘前后流入、流出的气流按时间平均、稳态处理来模拟螺旋桨工作，即这个圆盘对气流具有和螺旋桨桨叶相同的作用效果。根据螺旋桨的流动特点，分析等效盘气流参数的变化时，需假定：流体不可压；流动是定常的（稳定的）；等效盘前后压力是不连续的；轴向速度是连续的；周向速度不连续。

在距离桨叶中心为r 处取一长度为dr的桨叶剖面为研究对象，剖面如图1所示。

图1 螺旋桨桨叶剖面来流和气动力示意图Fig.1 Propeller section with relative velocities and forces

当前合速度V为螺旋桨桨盘来流与自身旋转来流的叠加。由安装角αg和来流角αi，可得当前桨叶截面的有效迎角αe。作用于当前微元段的升力Ld、阻力Dd、拉力Td和扭矩Qd分别为

其中ρ为气流密度，V为实际来流速度，c为当前微元段的翼型弦长，r为当前微元段距离旋转轴距离，CL，CD为微元段的升、阻力系数，需要提前根据实验数据或者CFD计算获取。

螺旋桨在旋转过程中，等效盘模型将桨叶微元段对流场的作用等效为时间平均的作用，通过对等效盘边界体积力的计算，带入控制方程源项J对流场进行迭代求解。值得注意的是，当前计算得到的体积力仅仅是螺旋桨桨盘的边界对气流作用，整体来看，流场的其他位置并未有这样的体积力作用。

假设桨盘在直角坐标系中，如图2（a）实线所示，其中-z方向为来流方向，螺旋桨桨轴所在直线与z方向直线重合。

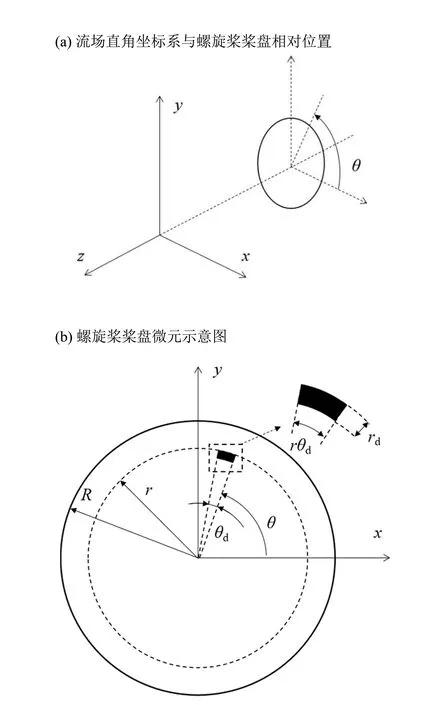
图2 螺旋桨桨盘和微元坐标系示意图Fig.2 Element of propeller disk in coordinate system

在螺旋桨桨盘中取一矩形微元，如图2（b）所示，其中dr为微元径向长度，rθd为微元周向长度，θ为微元段与x轴正方向的夹角。r为微元与圆心的距离，R为桨盘半径。

假设螺旋桨桨叶数量为N，长度为dr的桨叶剖面受气流的作用力为F，满足F=在一个周期内该矩形微元对气流作用的平均力为

将作用在气流上的体积力转换到直角坐标系

具体的等效盘求解过程如图3所示。

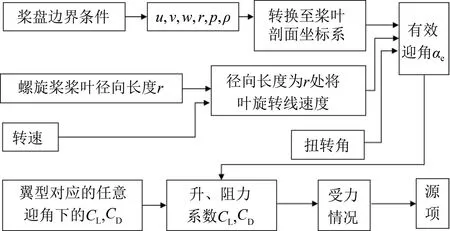
图3 等效盘模型求解流程示意图Fig.3 Solve flow chart of the actuator model method

基于等效盘的螺旋桨数值模拟方法本质上是将非定常流动的螺旋桨滑流通过在时序上的平均转化为定常流动，无法真实模拟螺旋桨转动过程中的流场细节。等效盘方法基于二维桨盘，忽略了三维效应，例如螺旋桨桨尖的涡流等复杂流动。本文通过修正系数的方式对螺旋桨旋转产生的涡流影响进行修正。

2 螺旋桨验证

算例主要参考X-57验证机单个分布式前缘螺旋桨的实验数据（Litherland et al.， 2017）和系列计算数据（Borer et al.， 2020），在不同前进比下验证本文等效盘方法的推力系数和功率系数的计算准确性。

2.1 研究对象

该型螺旋桨可收放，在起降阶段时工作，飞行器巡航时桨叶向桨轴折叠以减少飞行阻力，提高巡航效率。该螺旋桨外形参数如表1所示。其中桨毂直径为螺旋桨轴到桨叶的连接结构直径，3/4扭转角β3/4为螺旋桨桨叶在螺旋桨轴心到3/4螺旋桨半径处的扭转角度，通常将其作为桨距值，因此用于衡量桨叶的整体扭转。

表1 螺旋桨外形参数表Table 1 Profile parameters of the propeller

使用无厚度圆盘模拟螺旋桨，网格总量约53万，如图4所示。

图4 单个螺旋桨网格示意图Fig.4 Grids of single propeller

2.2 气动计算结果对比

选取5个不同前进比下的计算数据或者实验数据作为参考，如表2所示。

表2 螺旋桨工况设置和结果Table 2 The conditions and results of propeller

其中工况3的推力、功率系数数据为实验数据（Litherland et al.，2017），其余工况数据为Borer et al.（2020）在研究分布式动力飞行器在飞行阶段时的螺旋桨工况控制的计算结果。

本文采用等效盘方法对上述工况的计算结果与对比如表3 所示。可见，在不同前进比情况下，本文计算结果与实验或者数值计算结果拟合良好，推力系数相对误差最大为6.2%，功率系数相对误差最大为6.6%，这表明本文的等效盘模型在工程上能基本满足螺旋桨定常计算需要。

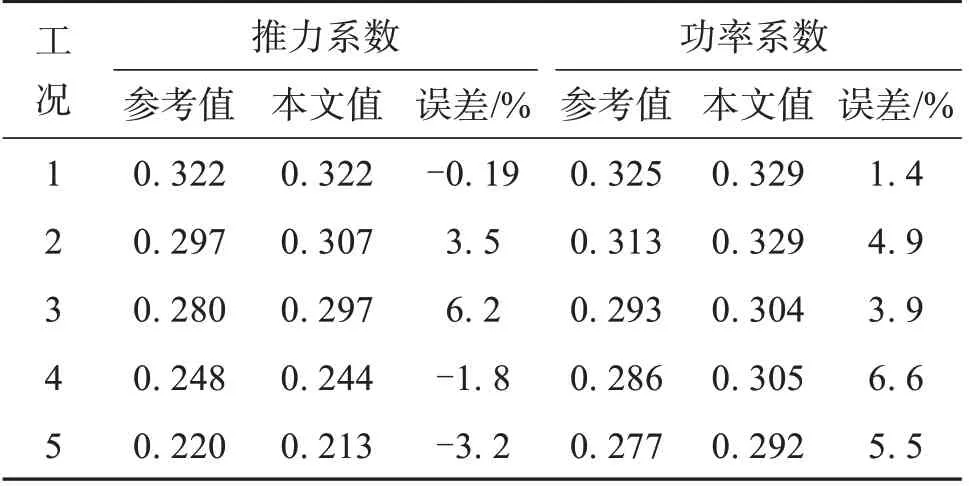
表3 螺旋桨计算结果与对比Table 3 Results and comparison of propeller computation

3 研究对象外形、网格与方法

NASA 的X-57 验证机在机翼前缘分布多个高升力发动机，在起降阶段时启动，在机翼表面制造大规模滑流区大幅提高当前整机的最大升力（Stoll et al.，2014）。Viken et al.（2017）在此基础上研究了适合滑流作用下的机翼翼型与襟翼类型，并优化了相关外形参数。本文在相关研究基础上，采取类似构型和布置，重点研究螺旋桨倾转对机翼的滑流气动特性变化。

3.1 计算对象

机翼及分布式螺旋桨外形如图5所示。采用平直机翼构型和半模计算外形，螺旋桨为其中无厚度圆盘，沿展向均匀分布在机翼前缘、螺旋桨中心相对机翼前缘距离交错分布，如图5（b）和（c）所示。机翼外形参数见表4。机翼采用富勒襟翼构型，在起降阶段展开并偏转，有效提高机翼最大升力系数。起降阶段的襟翼偏转角和分布式螺旋桨的转速参考Deere et al.（2017）设置见表5。

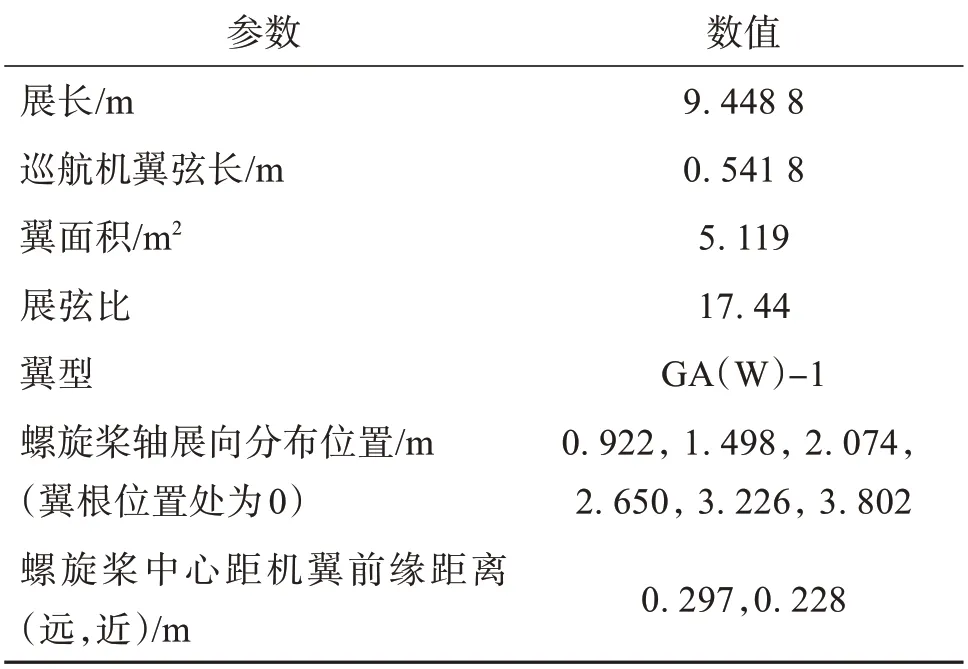
表4 机翼外形及螺旋桨分布参数表Table 4 Wing shape and propeller distribution parameters

表5 起降构型参数表Table 5 Take-off and landing parameters

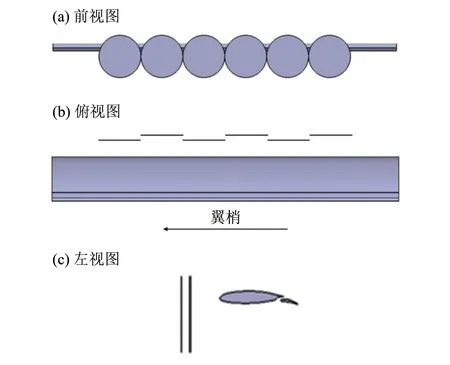
图5 分布式螺旋桨及机翼外形示意图Fig.5 Configuration of distributed propellers and the half wing

桨盘倾转角度定义如图6所示，该视图为翼梢到翼根方向正视图。将螺旋桨与机翼前缘距离简化为相同距离。螺旋桨中心相对机翼前缘位置为xc，桨轴相对机翼弦线的倾转夹角为θ，倾转中心为桨盘中心，相同视角下，顺时针倾转为正。zc为螺旋桨中心距离弦线距离，在螺旋桨倾转过程中保持不变。δ为襟翼偏转角，α为来流方向相对机翼弦线的迎角。

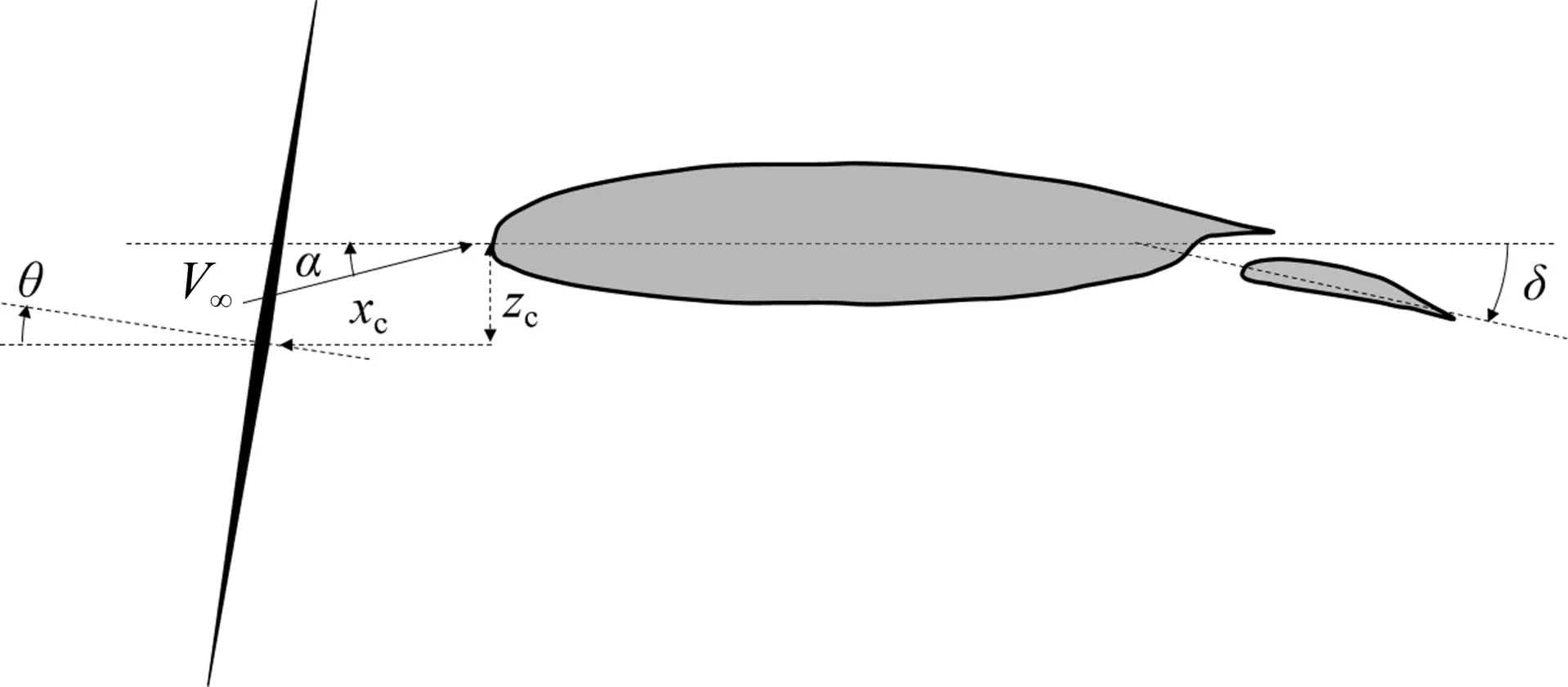
图6 螺旋桨相对机翼倾转示意图Fig.6 Tilt of propellers relative to the wing

为了研究螺旋桨倾转带来的气动特性影响，分别对起降构型调整螺旋桨桨盘相对机翼弦线的倾转角度，并且设置不同的迎角，如表6所示。在机翼安装角为5.5°情况下，设置机翼来流迎角为5.5°模拟飞行器在0°迎角下的飞行状态。设置桨盘倾转角为-5.5°使得飞行器在0°迎角时螺旋桨推力水平，倾转角的设置间隔约为4°.

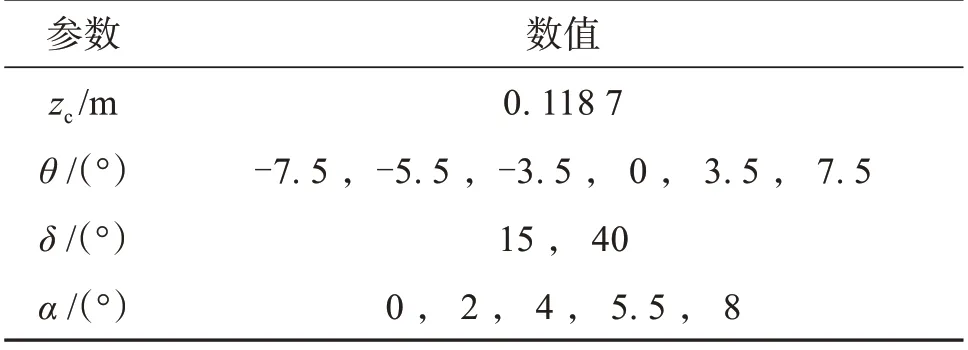
表6 螺旋桨相对机翼参数表Table 6 Parameters of propeller relative to the wing

3.2 网格介绍

采用非结构网格，半模网格总数约为455 万，计算雷诺数约为1.24×106（基于巡航时机翼弦长），第一层网格高度设为1.0×10-5m，y+=1.使用无厚度的圆盘模拟螺旋桨，采用等效盘方法计算。起飞构型机翼网格如图7所示。

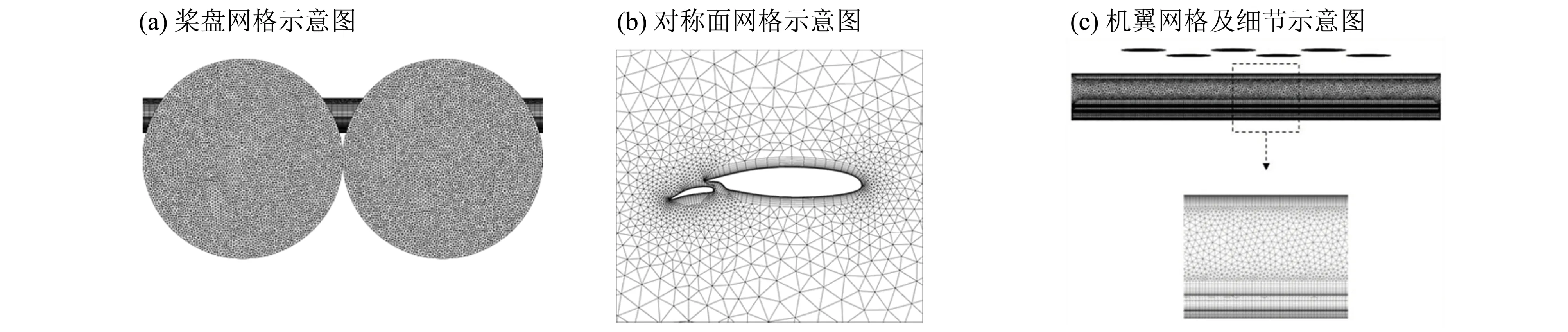
图7 机翼及桨盘计算网格Fig.7 Computational grids of wing and actuator disks

为了研究网格数量对计算结果的影响，图8给出迎角为4°，螺旋桨相对机翼倾转角为-5.5°时，机翼在起飞状态下升阻力系数随着网格数量变化的曲线。可以看出，当网格数超过1 500 万时，升力系数和阻力系数变化幅度较小，整体呈现收敛趋势。选取首套网格与网格数量为3 012 万的网格做比对，升力系数相差0.049 8，变化率为2.402%，阻力系数相差0.005 14，变化率为3.02%，整体变化幅度不大。考虑到本文主要研究螺旋桨倾转角对机翼气动特性的影响规律，原网格的计算精度基本满足本文对趋势性研究的计算精度要求。为了在后续的研究中节约计算成本，本文计算所用网格均采用原网格的生成方法。

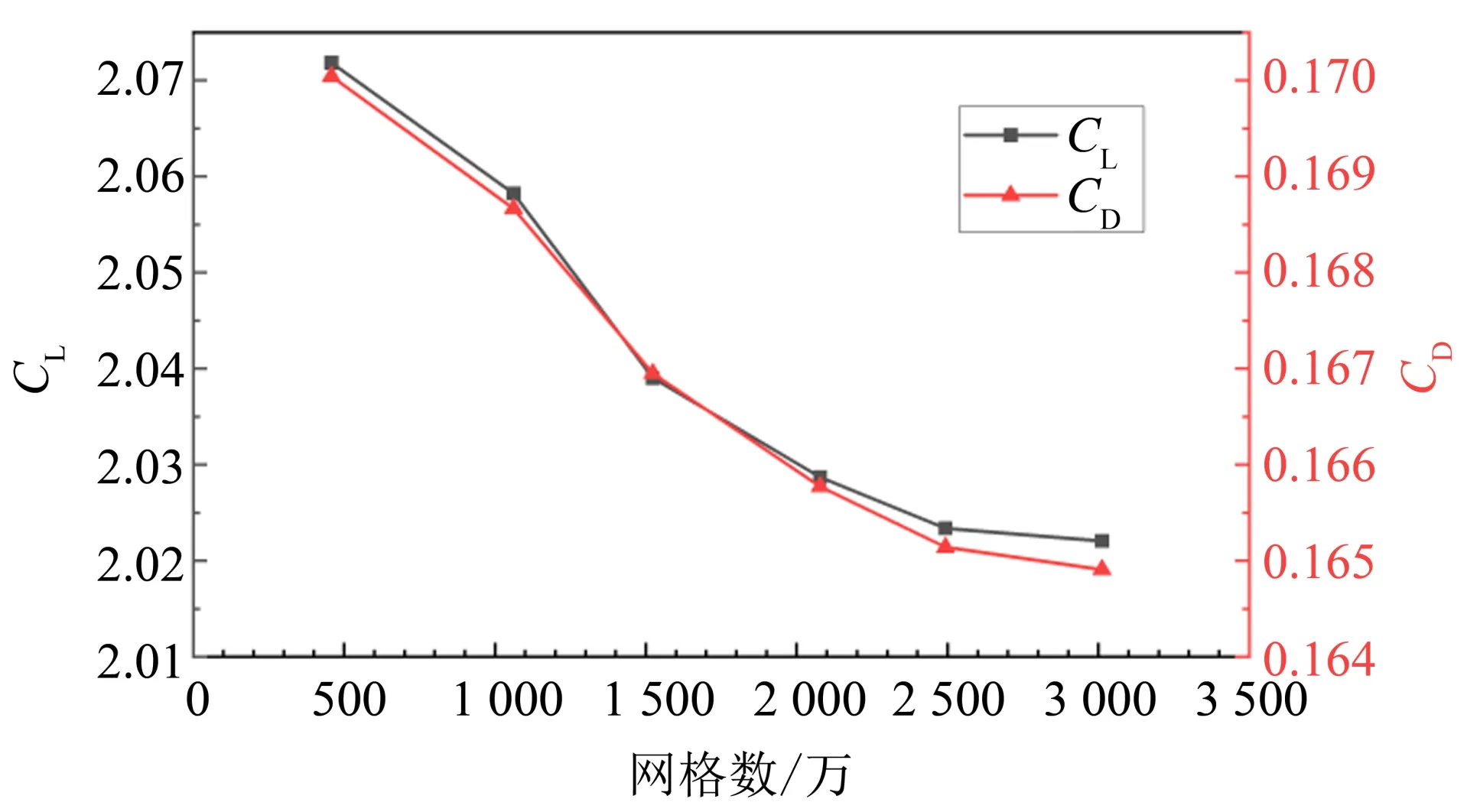
图8 机翼升阻力系数随网格量变化趋势Fig.8 Variation trend of lift and drag coefficients with grid quantity

4 计算结果与分析

4.1 螺旋桨滑流对机翼气动特性的影响

在机翼安装角为5.5°情况下，假定起降阶段分布式推力方向和0°迎角下的来流方向一致，此时螺旋桨倾转角为-5.5°。分别给出在螺旋桨倾转角度为-5.5°下，起降构型在相同来流速度下，螺旋桨工作下和不安装螺旋桨情况下迎角-8°～24°的机翼升阻力系数。如图9所示。

由图9（a）可以看出，对于起飞构型，无滑流影响的机翼最大升力系数为2.343，滑流影响下机翼的最大升力系数提高到3.526，对应的失速迎角分别是16°和14°.在升力系数线性增长段，滑流影响下机翼的升力线斜率大于无滑流机翼的升力线斜率。失速阶段，无滑流影响的机翼升力系数下降较为陡峭，滑流影响下的机翼升力系数下降更为平缓。

对于降落构型，无滑流影响的机翼最大升力系数为2.407，滑流影响下机翼的最大升力系数提高到4.445，提高了84.7%，对应的失速迎角为14°不变。在升力系数线性增长段，滑流影响下机翼的升力线斜率更大。在失速阶段，滑流影响下的机翼升力系数下降更为平缓。

相对起飞构型，由于降落构型有着更大的襟翼偏转角，故无滑流影响下的机翼最大升力系数所对应的迎角更小。此外，滑流影响下，降落构型的最大升力系数相对起飞构型的最大升力系数更大，在升力下降阶段升力系数下降趋势更加平缓。

由图9（b）可以看出，无论有无滑流影响，阻力系数-迎角基本呈二次关系。随着迎角的增大，各构型的机翼阻力系数均逐渐增加，滑流影响下的机翼阻力系数显著高于无滑流的机翼阻力系数，其中，滑流影响下降落构型的机翼阻力系数最大。随着迎角增大，滑流影响下机翼比无滑流影响的机翼阻力系数增长更快。

由图9（c）可以看出，无滑流影响下，起降构型机翼升阻比均随着迎角的增大先增加后减小，起飞和降落构型最大升阻比对应的迎角分别为0°和4°.在失速段，机翼升阻比下降较为陡峭。滑流影响下，除-8°迎角外，起降构型机翼的升阻比均有所减小，起飞构型升阻比随着迎角的增大先增加后减小，升阻比最大值对应的迎角为-2°.降落构型升阻比随着迎角的增大逐渐减小，下降趋势较为平缓。

可以看出，无论是起飞还是降落构型，滑流影响下，最大升力系数和升力线斜率均有所提高，失速段的升力系数下降更为平缓；在滑流影响下降落构型比起飞构型的最大升力系数更大，原因是降落构型的螺旋桨转速更大，襟翼偏转角更大。

图10 给出了在4°迎角下，起降构型在有/无滑流作用下上、下机翼压力系数CP分布云图。可以看出在滑流影响下，机翼上表面前缘低压区域扩大，且整体压力系数更小。同样地，在机翼下表面高压区域更大更显著。相比起飞构型，由于降落构型的襟翼偏转角更大，机翼前缘分布的螺旋桨转速更大，机翼上下表面的低压区和高压区更大更明显，因此机翼整体的升力系数更大。

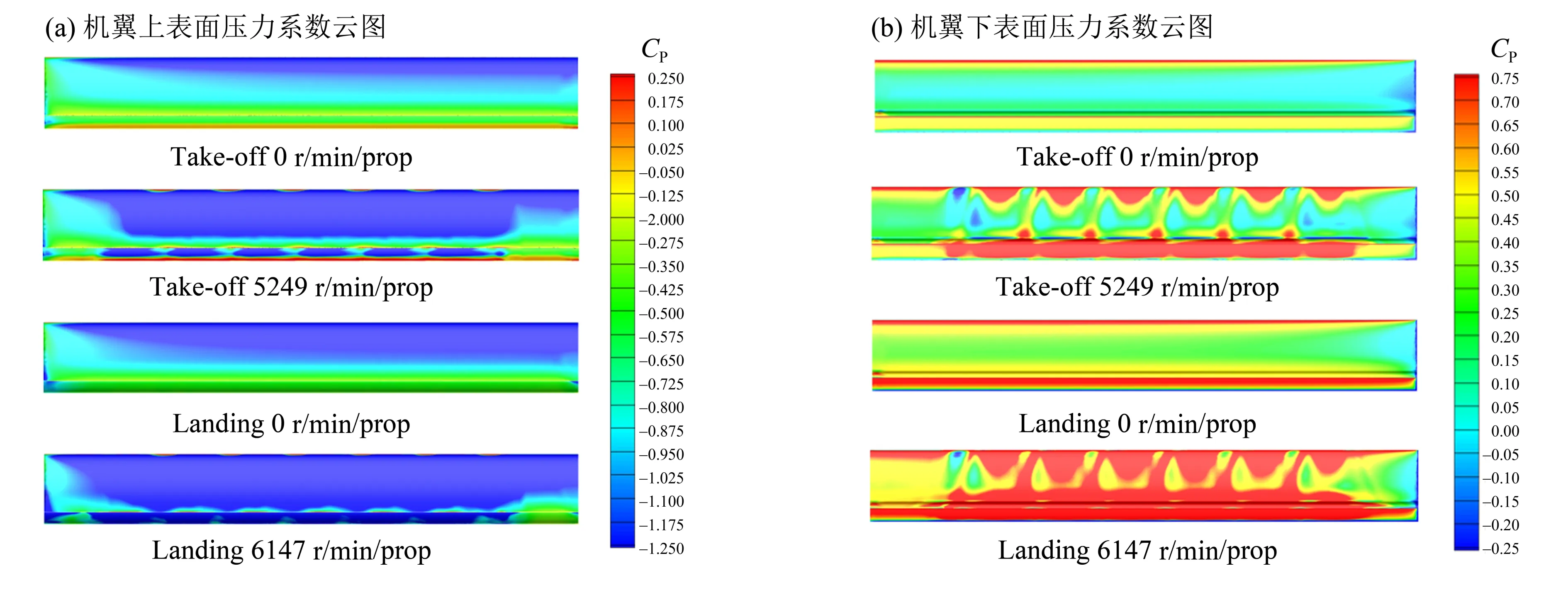
图10 机翼上、下表面压力系数云图Fig.10 Pressure coefficient distribution of the wing

整体来看，在分布在机翼前缘的螺旋桨滑流影响下，机翼在起降构型下的升力系数均有所提高，升力系数线性增长段斜率增大，失速阶段的升力系数下降幅度减缓，阻力系数有所增加。主要是因为滑流影响下，机翼上表面的低压区域扩大，且整体压力系数更小，机翼下表面的高压区域扩大，整体的压力系数更大，扩大的压差使得机翼整体的升力系数变大。

为了进一步说明机翼不同展向站位处滑流对机翼的影响，给出机翼不同截面示意如图11所示，53.0%翼展站位处在螺旋桨桨叶下行侧，59.1%翼展处截面在螺旋桨桨叶上行侧。机翼不同展向站位处压力系数分布对比如图12 所示。其中CP为压力系数，x/c为翼型弦向长度与弦长比。

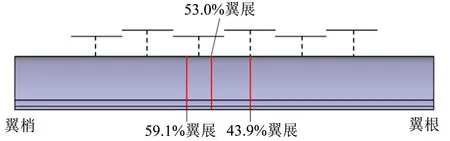
图11 机翼截面示意图Fig.11 Sections distribution of the wing

图12 不同机翼展向处截面表面压力系数分布Fig.12 Pressure coefficients distribution on wing surface at different sections

可知，在43.9%翼展截面为螺旋桨中心处截面，由于螺旋桨轮毂的存在，使当地滑流效果较小，在机翼前缘部分，滑流有限地扩大了机翼上、下表面压力差，由于降落构型襟翼偏转角更大，因此较小强度的滑流仍然能有效扩大襟翼上、下表面压力差。

滑流有限地增加53.0%翼展截面处机翼上下表面压力系数差，而在59.1%翼展截面处显著增加了机翼上下表面压力系数差，增大了机翼升力。59.1%翼展截面处在螺旋桨旋转带动桨叶上行侧，盘后气流速度在竖直方向上的分量增加，机翼有效迎角增加。53.0%翼展处截面在螺旋桨旋转带动桨叶下行侧，盘后气流速度在竖直方向上的分量减小，减小了机翼有效迎角。

4.2 螺旋桨倾转对起飞构型气动升力系数的影响

螺旋桨倾转时机翼受力情况如图13所示。

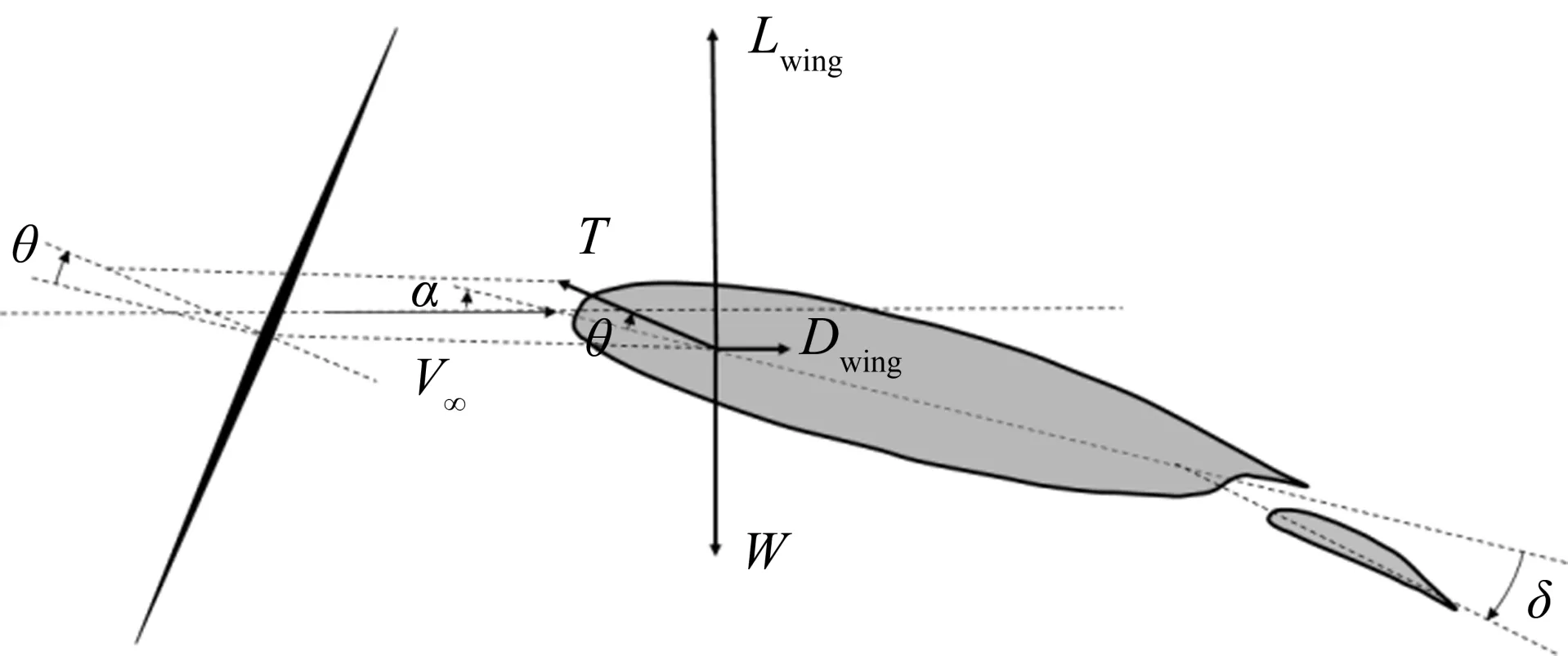
图13 机翼受力示意图Fig.13 Forces on the wing

其中T，Lwing，Dwing和W分别为单个分布式螺旋桨平均推力，机翼气动升力，机翼气动阻力和重力。θ，α和δ分别是螺旋桨相对机翼弦线的倾转角（顺时针方向为正）、来流迎角和襟翼偏转角。

在螺旋桨倾转情况下，机翼有效升力包括分布式螺旋桨推力在升力方向上的分力和气动升力。机翼气动升力系数CL，wing和有效升力系数CL，eff满足

其中n为螺旋桨数量，ρ为当地气流密度，V为来流速度，S为机翼面积。

在不同螺旋桨倾转角下，CL，wing和CL，eff随着迎角的变化如图14所示。

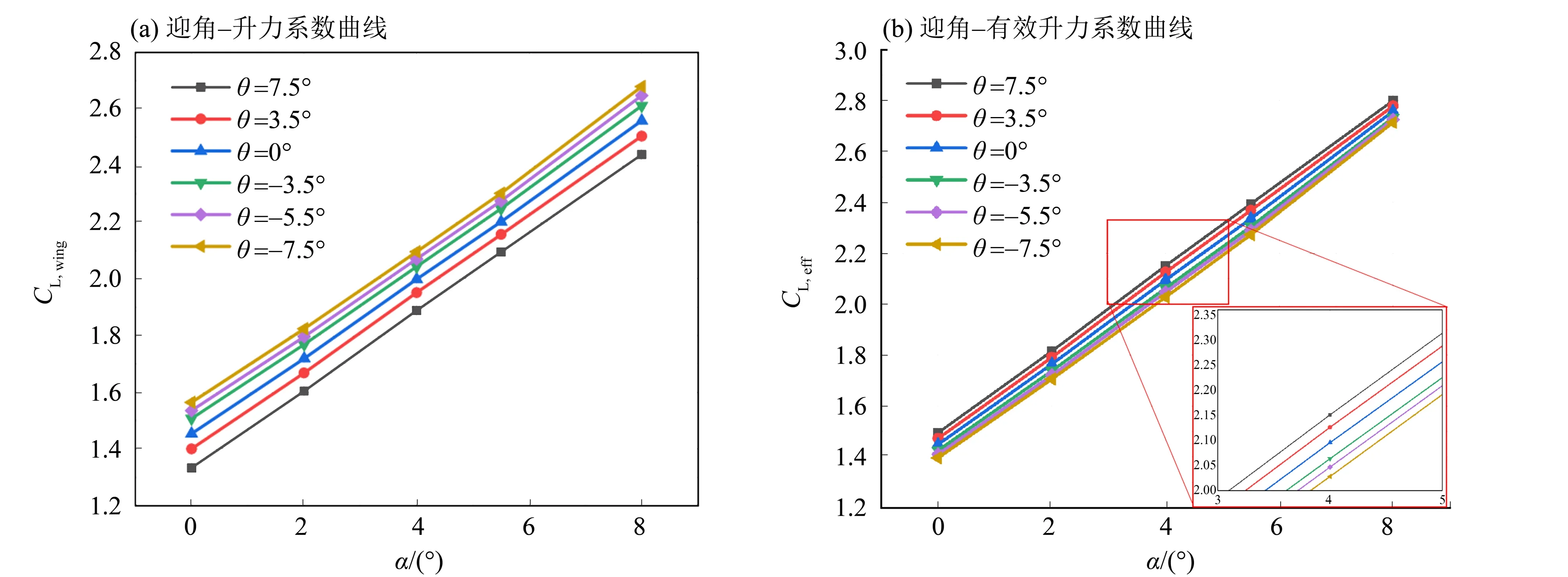
图14 不同螺旋桨倾转角下迎角-升力系数/有效升力系数曲线Fig.14 Angles of attack-lift coefficient/effective lift coefficient at different propeller tilt

由图14 可见，无论桨盘倾转角度如何，机翼升力系数随着迎角线性增长。另外，在相同的迎角下，随着桨盘倾转角的减少，CL，wing逐渐增大，而CL，eff的趋势恰好与之相反，在计算范围内，倾转角为7.5°时，有效升力系数最大。

当α+θ＜0 时，桨盘相对来流方向逆时针偏转。一方面，对于主机翼和襟翼来说，由于桨盘逆时针倾转，使得分布式螺旋桨产生的滑流相对于机翼的迎角变大，使得主机翼产生了更高的升力。另一方面，螺旋桨产生的推力在竖直方向上的分力与升力方向相反，因此减少了有效升力。相反的，如果桨盘顺时针偏转，那么由于滑流相对机翼的迎角变小，那么主机翼产生更小的升力，而螺旋桨的推力在竖直方向上的分力则作为升力的补充，使得有效升力增加。

在给定迎角下，不同倾转角下的分布式螺旋桨对机翼的气动影响也不尽相同。为了进一步分析螺旋桨倾转对机翼的气动影响，如图15 所示为给定迎角为4°、8°下，桨盘倾转角为7.5°和-3.5°时，在螺旋桨轴心截面处压力系数云图。

由图15（a），（b）可见，在迎角为4°情况下，相比倾转角为7.5°的构型，倾转角为-3.5°构型在机翼前缘处有着更大更明显的正压区，这使得该构型受到更大的气动升力。图15（c），（d）显示了在迎角增大情况下，机翼前缘的正压区下移，范围扩散到襟翼下表面大部分区域，显著提高了机翼整体升力。相比倾转角度为7.5°的构型，倾转角度为-3.5°的构型机翼前缘和襟翼下表面正压区范围更大。

通过对升力系数的计算和压力系数的云图的分析，可以看出，螺旋桨桨盘在顺时针方向的倾转通过提高了机翼的有效迎角从而改变了流场压力分布，进而提高了机翼升力系数。

4.3 起降构型的最佳倾转角度分析

飞行器在0°迎角飞行状态下，机翼安装角固定为5.5°，为了研究螺旋桨倾转对固定迎角下机翼的有效升力系数的影响，设定起降阶段机翼迎角均为5.5°.计算得到不同螺旋桨倾转角下的升力系数和有效升力系数。

本文基于等效盘的螺旋桨数值模拟方法无法真实模拟螺旋桨转动过程中的流场细节，对螺旋桨桨叶有效迎角过大时的气动分离的情况模拟准确性不足。当螺旋桨转速不变时，螺旋桨倾转角过大时（超过+45°或小于-45°），螺旋桨桨叶有效迎角较大，可能出现大面积的气动分离，本文建立的等效盘方法不再适用。本文螺旋桨倾转角的计算范围设置为-10°～30°.

4.3.1 螺旋桨倾转对起飞构型的有效升力系数的影响为了获取最大有效升力系数和对应的螺旋桨倾转角，使CL，eff对θ求偏导，根据式（6），（7）有

进一步求导可得

给定当前迎角为5.5°情况下，得到θ-T（α，θ）的计算结果，对θ-T（α，θ）进行多项式拟合，拟合结果满足

且

其中拟合优度R2越接近1拟合度越好。

计算结果图和拟合结果如图16 所示，CFD 计算结果和拟合曲线符合较好。

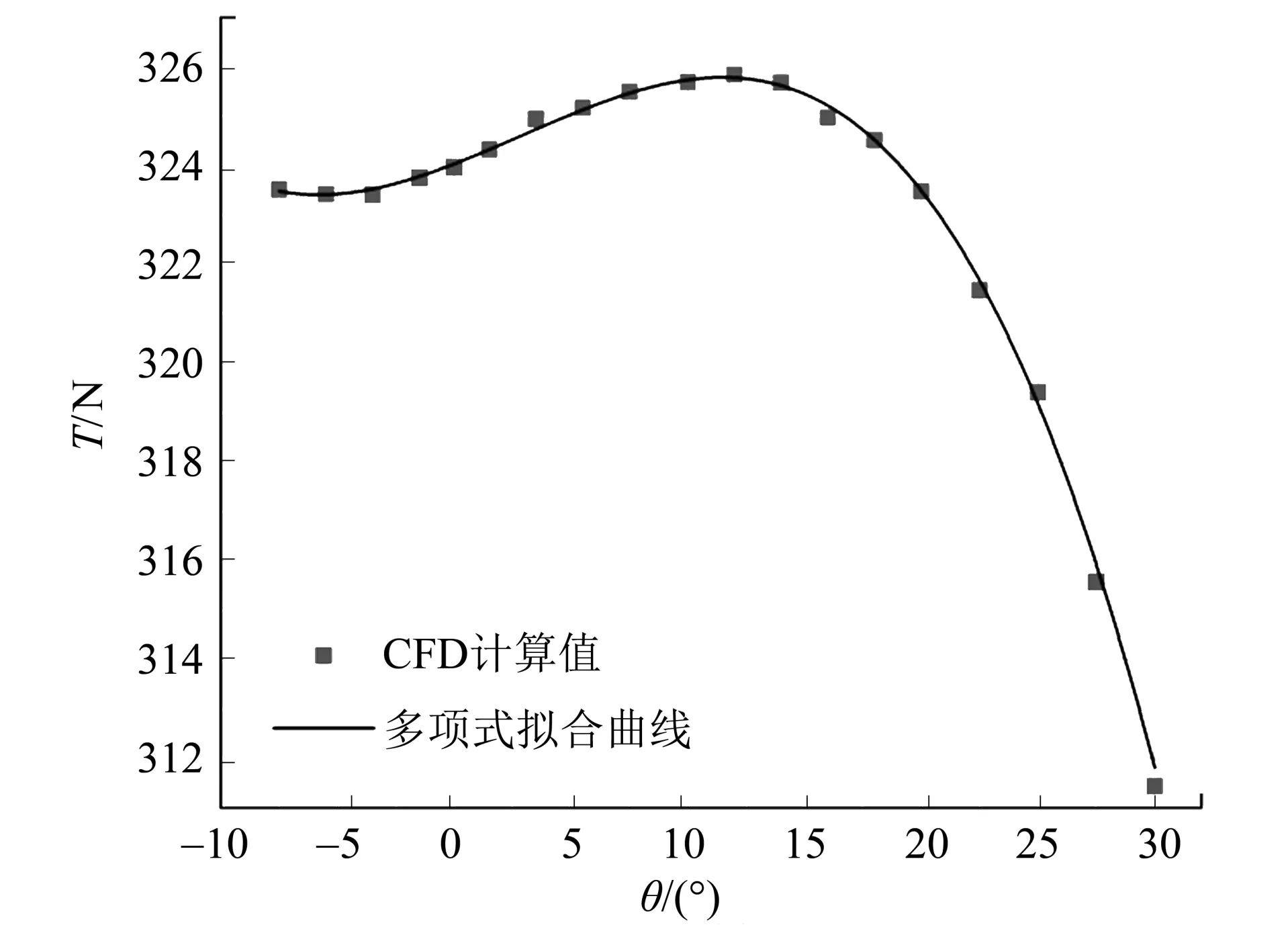
图16 起飞时单个螺旋桨推力随倾转角的变化及拟合曲线Fig.16 Thrust of single disk varying with angle of propeller disk inclination and fitting curve at take-off state

同样给定当前迎角为5.5°情况下，对θ-CL，wing进行多项式拟合，可得

且

计算结果和拟合曲线如图17 所示，可见CFD计算结果中CL，wing和θ近似呈二次关系，和拟合曲线匹配。

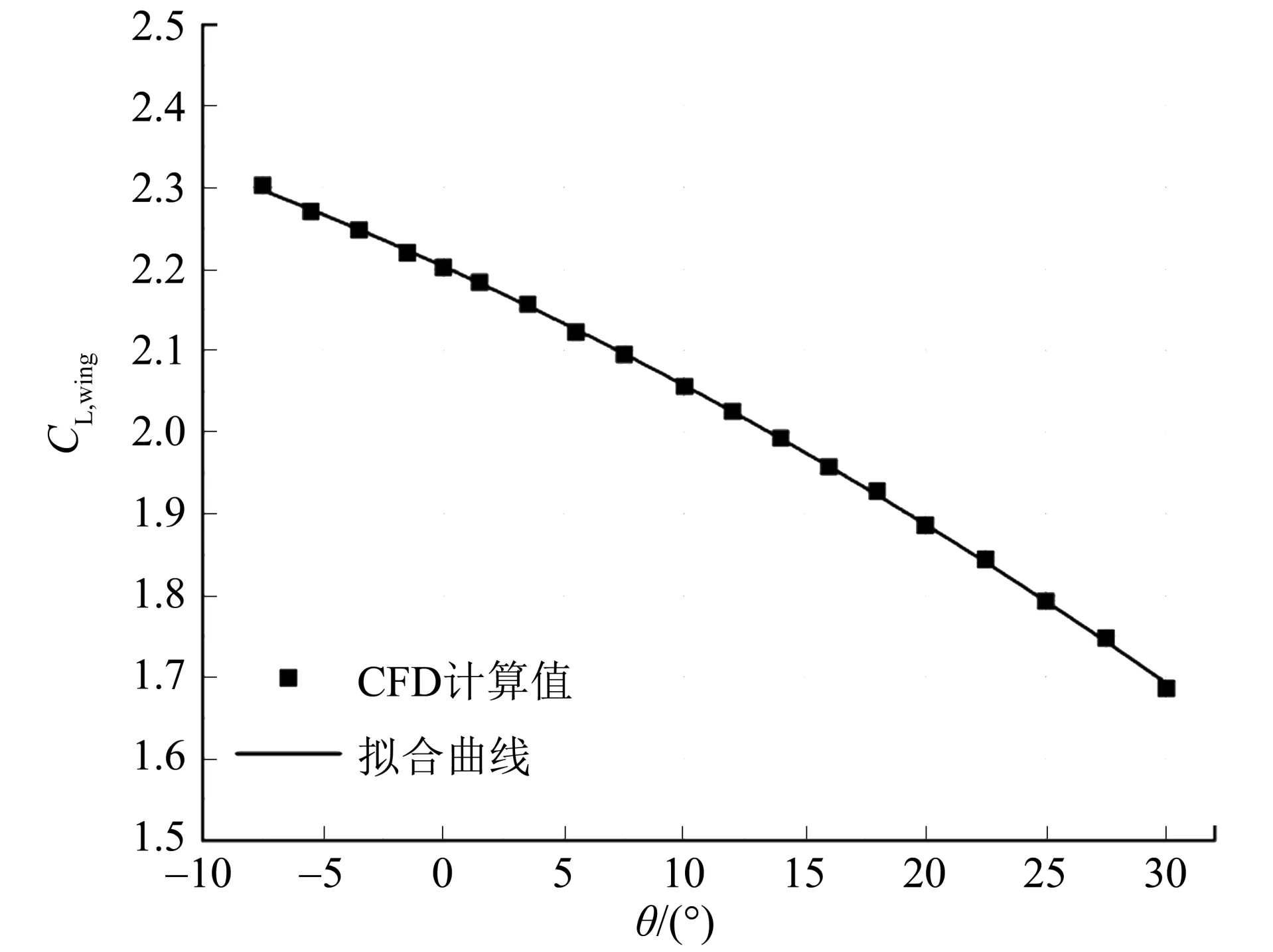
图17 起飞时螺旋桨倾转角-升力系数及拟合曲线Fig.17 Lift coefficient varying with angle of propeller disk inclination and fitting curve at take-off state

将拟合结果式（10），式（11）和式（13）及其他相关数据代入到式（9）中，得到CL，eff对θ偏导估计如式（14）所示。

其中

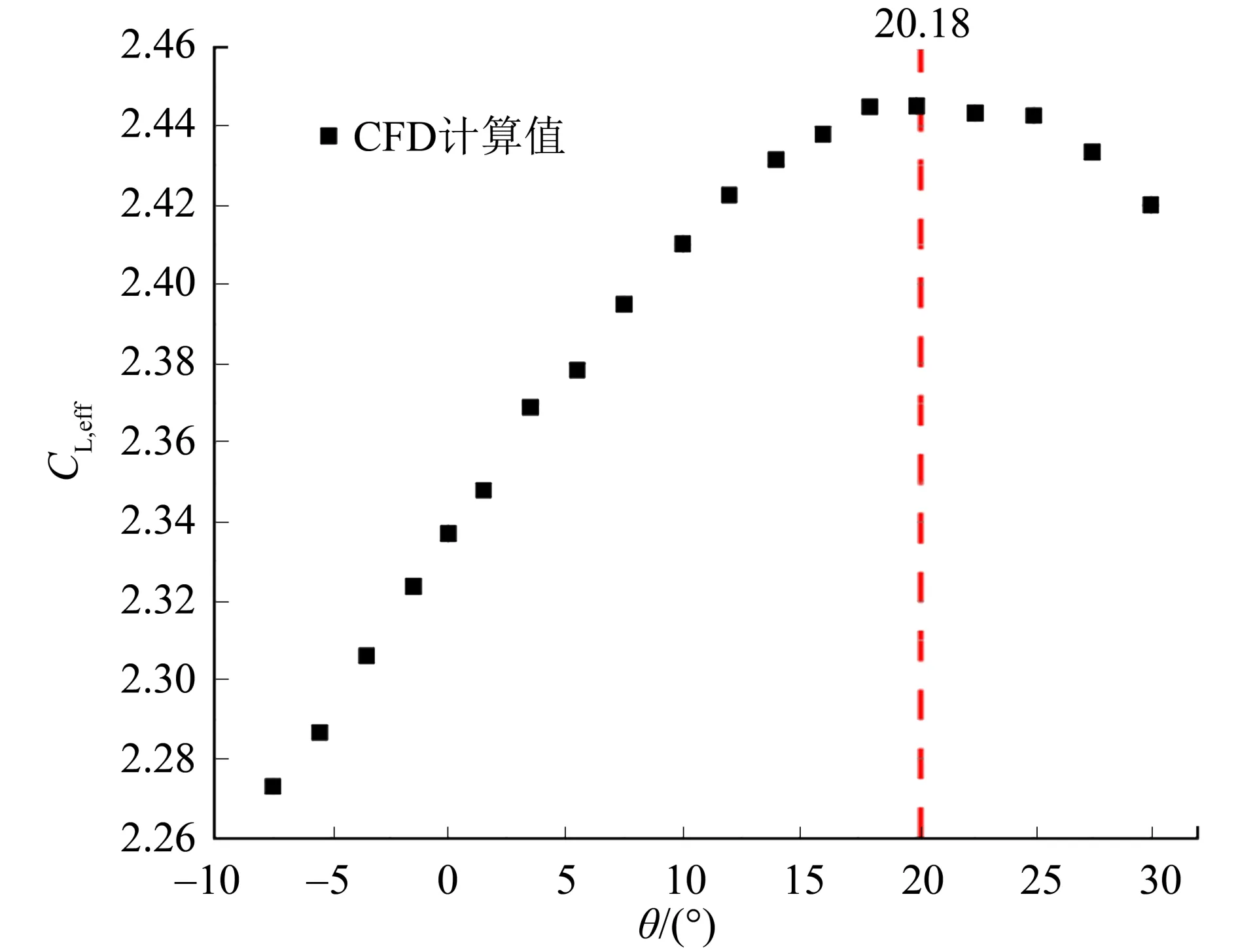
图18 起飞时螺旋桨倾转角-有效升力系数结果Fig.18 Efficient lift coefficient varying with angle of propeller disk inclination at take-off state

4.3.2 螺旋桨倾转对降落构型的有效升力系数的影响在迎角为5.5°情况下，对θ-T（α，θ）进行多项式拟合可得

且

可得计算结果图和拟合曲线如图19 所示，当θ为12°，14°时，CFD 计算结果数据点与拟合曲线有较明显的偏离，但CFD 计算值总体和拟合曲线符合较好。

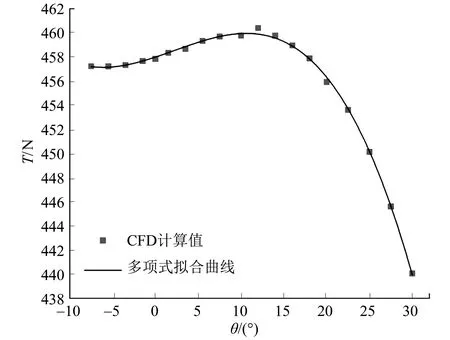
图19 降落时单个螺旋桨推力随倾转角的变化及拟合曲线Fig.19 Thrust of single disk varying with angle of propeller disk inclination and fitting curve at landing state

给定迎角为5.5°情况下，对θ-CL，wing进行多项式拟合可得

且

计算结果图和拟合曲线如图20 所示，CFD 计算结果和拟合曲线匹配。

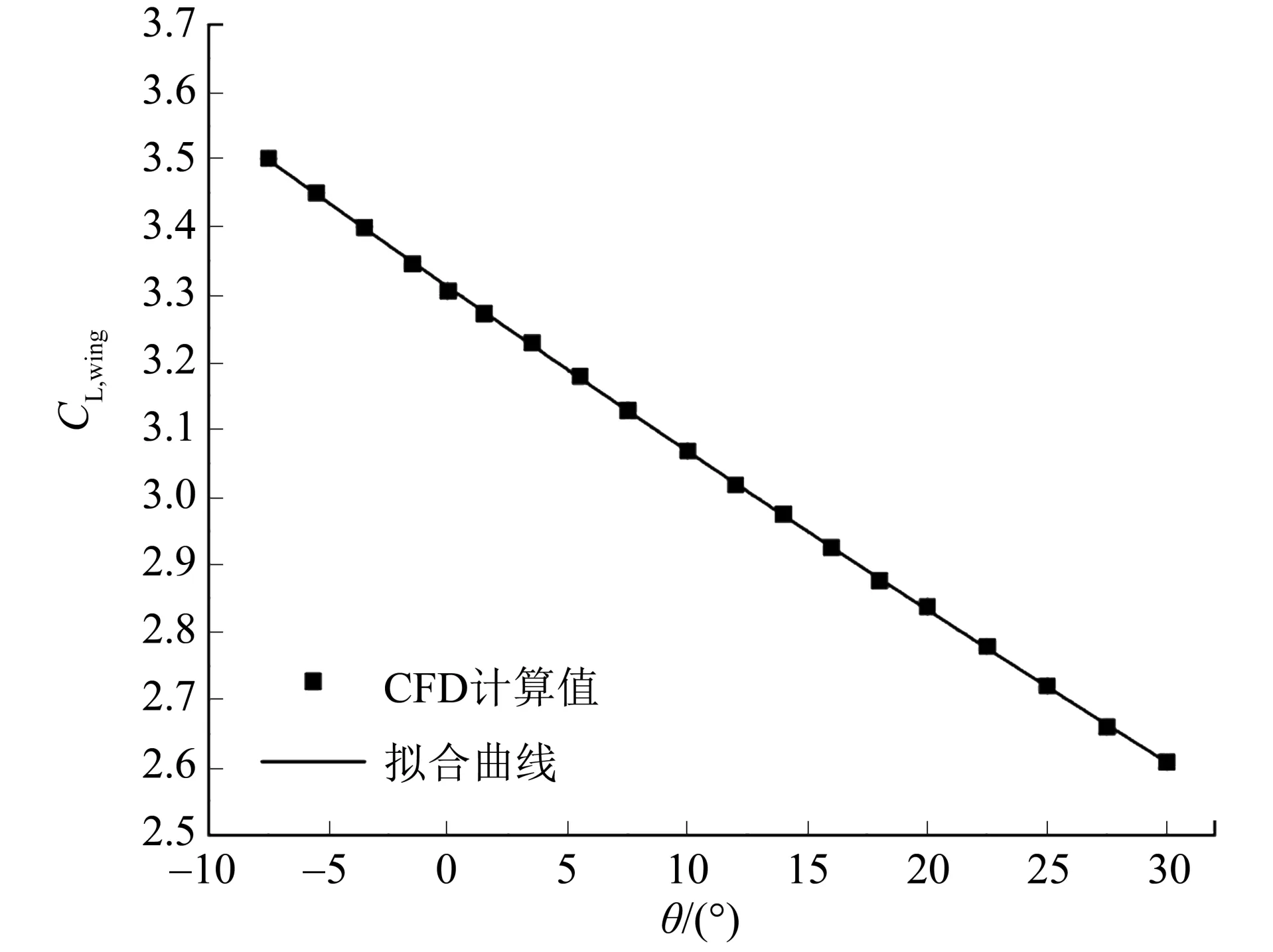
图20 降落时螺旋桨倾转角-升力系数及拟合曲线Fig.20 Lift coefficient varying with angle of propeller disk inclination and fitting curve at landing state

将拟合结果式（15）～（16）和式（18）以及其他相关数据代入到式（8）中，得到估计式

其中

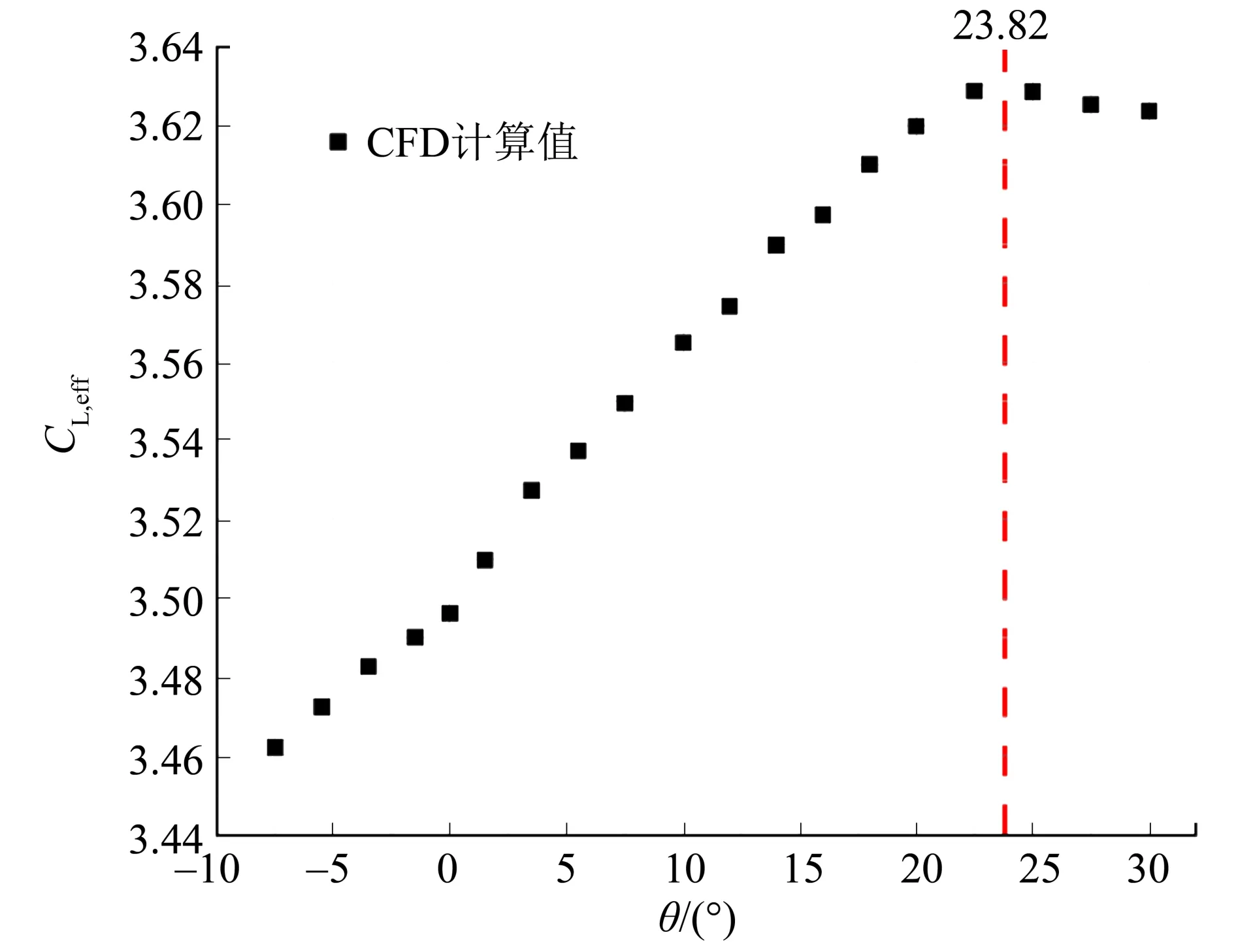
图21 降落时螺旋桨倾转角-有效升力系数结果Fig.21 Efficient lift coefficient varying with angle of propeller disk inclination at landing state

由图21 可知，计算得到的最大有效升力系数对应的螺旋桨倾转角在22.5°左右，此时有效升力系数为3.628 8.计算结果符合拟合结果。

综上可知，螺旋桨倾转通过改变滑流对机翼的迎角的方式，对机翼的最大升力系数造成影响，通常来说，螺旋桨顺时针倾转使得滑流对机翼的迎角变小，因此减小了机翼的最大升力系数。但是由于螺旋桨倾转导致推力的分力与气动升力叠加，改变了机翼的有效升力。无论是起飞还是降落构型，随着螺旋桨倾转角的变大，机翼的有效升力系数总是呈现先增大后减小的趋势。

5 结 论

本文基于等效盘模型，分析了分布式螺旋桨滑流对带富勒襟翼的平直机翼在起降阶段的气动性能的影响。并对分布式螺旋桨倾转对机翼气动升力系数和有效升力系数的影响结果进行分析。

1）本文等效盘模型是可靠的。对于通用的用于计算定常状态的螺旋桨的等效盘模型，总结了等效盘模型的计算流程。计算算例和实验算例的对比结果表明，计算结果和实验结果吻合良好，验证了等效盘的计算可靠性。

2）分布式螺旋桨滑流对机翼的气动特性影响明显。分别对起飞、降落构型下有无滑流影响的情况进行比对计算，计算结果表明，对于不同构型，滑流都使得：机翼的最大升力系数增大，升力线系数提高，升力下降阶段升力系数下降趋势更加平缓。

3）分布式螺旋桨的倾转改变了机翼气动升力系数。螺旋桨在不同方向的倾转通过改变滑流方向的方式改变机翼的实际迎角，从而改变机翼升力系数。螺旋桨顺时针倾转过程中，产生的滑流与来流叠加共同减小了机翼的实际迎角，降低了机翼的升力系数。

4）分布式螺旋桨的倾转改变了机翼有效升力系数。螺旋桨倾转过程中，螺旋桨推力沿着升力方向的分力和气动升力共同影响了机翼的有效升力系数。计算结果表明，对于起飞构型，当螺旋桨倾转角为20.18°时，有效升力系数达到最大约为2.445 1，对于降落构型，当螺旋桨倾转角为23.82°时，有效升力系数最大约为3.628 8。