基于PFC的基坑爆破数值模拟及安全性分析*

罗仁宇， 李奇志， 黄云进， 杨耿超， 余毛毛， 祖公博， 姚清河

1.中山大学航空航天学院，广东 深圳 518107

2.中建二局华南分公司，广东 深圳 518048

为了满足国家经济发展及人民日常出行的需求，地下交通出行逐渐成为目前的主流方式。因此，基坑开挖深度及开挖规模不断增大。基坑深层部分通常采用爆破的方式进行施工，但部分基坑与周围建筑相隔紧密，如何在深层岩石层爆破施工的同时保证周围建筑及相关基础设施的安全变得尤为重要。针对这一问题，学界从现场监测、数学模型、人工智能等方面做了许多研究。王德宝等（2015）通过对现场爆破过程进行监测，研究了减振孔、减振爆区对于减震的影响；宗琦等（2008）通过数学方法，结合现场监测，对爆破速度与爆破装药量之间的数据进行线性拟合，发现了爆破振动衰减的规律，并提出了减震的相应措施；刘先林等（2008）在线性回归预测方法的基础上，结合人工智能，运用Back Propagation 神经网络法对振动速度进行了预测。但由于基坑环境的复杂性与现有模型的局限性，目前对爆破过程引起的地面振动响应还严重依赖专家的经验判断，缺乏可信度及准确性。

随着计算机技术的高速发展，数值模拟逐渐成为了研究爆破的有力“可视化”试验手段。王鸿运（2009）使用有限元计算软件ANSYS，研究了振动速度与装药量之间的关系，以及振动速度随距离的变化关系；马晴（2019）使用ANSYS 对不同起爆方式以及不同起爆顺序下的岩石爆破进行了模拟，发现：反向起爆相对于正向起爆来说影响较大，逐孔起爆更有利于降低爆破产生的振动；鲁啸龙和胡辉（2018）使用有限差分法软件FLAC3D研究了新建隧道开挖爆破模型，并对速度结果进行了分析。然后，结合安全控制标准值，研究了对既有隧道的影响；范晓强（2020）研究了基坑开挖爆破对邻近地铁的影响。研究过程中，使用FLAC3D软件从速度、位移和力场三个方向展开分析，得到了基坑爆破振动速度与距离的衰减关系。

传统的有限元方法和有限差分方法均难以模拟岩石爆破近区的大变形过程，如岩体爆破过程中的抛掷现象。离散单元法（DEM，discrete element method）的基本思想是将不连续单元体表示为独立单元的集合，并将每一个单元作为一个独立对象来分析，接触的单元之间互相传递力与力矩，由此产生运动与变形。相对于有限元、有限差分等网格方法，DEM 的主要优势在于其能够处理复杂的颗粒间相互作用和非线性力学行为，而无需使用网格。DEM 既不需要进行网格化处理，也不需要自适应网格方法来适应颗粒大小和形状的变化，因此DEM 可以更加高效地模拟颗粒流问题。由于DEM 能够较好解决岩土介质的大变形问题，在岩土工程中得到了广泛的发展。众多学者应用DEM 对岩石爆破过程做了许多研究 （苏都都等，2012；崔铁军等，2017；Qiu et al.，2020），但在基坑爆破方面的数值模拟尚不多见。

基于穗莞深城际超深工作井爆破项目，本文通过颗粒膨胀方法来模拟爆破作用，验证离散单元法模拟爆破过程的合理性。通过分析基坑环境，合理构造模型，探究了不同起爆条件下引起的速度变化，评估了爆破对附近建筑物产生的影响。采用颗粒膨胀法来模拟爆破的加载过程，拓展了离散单元法的应用场景，并为基坑爆破提供了理论参考依据。

1 离散单元法模拟爆破过程

1.1 离散单元法

当使用有限差分等方法时，需要将物理域离散化为网格，并在网格节点上求解物理量的数值。然而，在颗粒流等含有大量颗粒的问题中，由于颗粒之间的相互作用和运动具有高度非线性和不连续性，这些问题的网格化处理将导致网格数量急剧增加，并增加计算的复杂度和计算量。此外，在颗粒流等问题中，颗粒的大小和形状可能会随时间发生变化，因此需要使用自适应网格方法来确保网格足够细致。这些因素导致使用传统的网格方法模拟颗粒流问题变得困难和耗时。离散单元法由Cundall（1971）提出，最初的设想是研究一些非连续介质的力学问题。后来，Cundall 和Strack（Cundall et al.， 1980）提出了模拟颗粒体的二维程序，并在动光弹模拟中验证了实验结果。本文采用基于离散单元法的颗粒流程序（PFC，particle flow code）模拟基坑开挖爆破过程，并评估爆破对周围建筑的振动影响。PFC在模拟不同的岩土体时，可选择不同的接触模型。本文采用线性接触模型模拟一般土体，采用平行粘结模型模拟岩体（Potyondy，2007），如图1 所示。线性接触模型只能传递力的作用，它由相互平行作用的线性和阻尼分量构成，线性分量由弹簧和摩擦键组成，提供线弹性摩擦行为，而阻尼分量由阻尼键提供粘滞行为。平行粘结模型在线性接触模型的基础上增加了粘结键，它们作用在一个有一定大小的接触平面上，在传递力的时候还可以传递力矩，一旦切向和法向应力超过平行粘结的粘结强度，粘结功能就会发生断裂破坏。

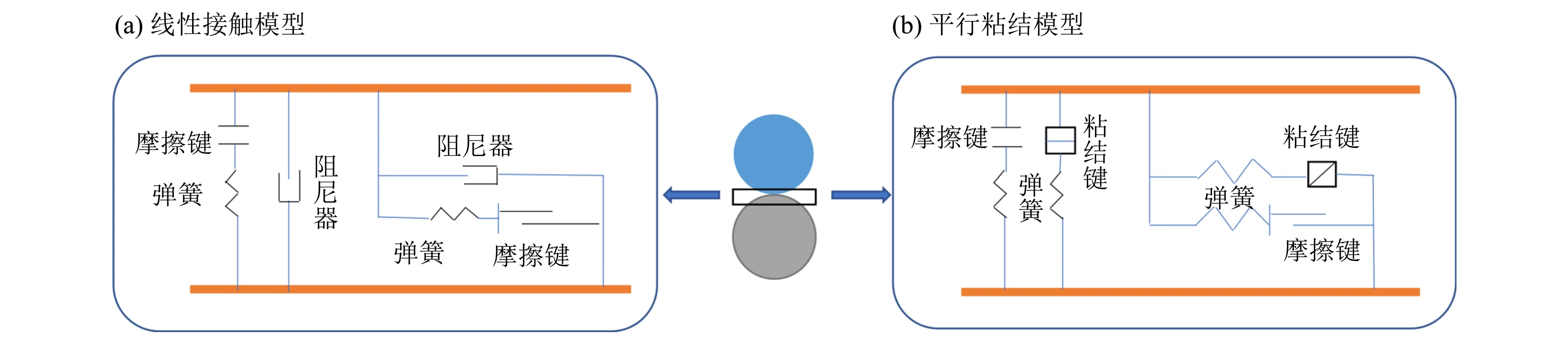
图1 接触模型图Fig.1 Structure of contact model

1.2 DEM模拟炸药爆破荷载

本文采用颗粒膨胀法来近似模拟炸药爆破（Yang et al.，2019；黄尘等，2022；袁增森等，2022），如图2 所示。在PFC 中，首先构造半径为r0的圆形区域作为炮孔，并在其中添加半径为r0的炸药颗粒。通过PFC 内置函数使炸药颗粒半径逐渐增加，当其接触到炮孔壁处的外围颗粒时，如果继续增加炸药颗粒半径，将会与外围颗粒产生重叠量。

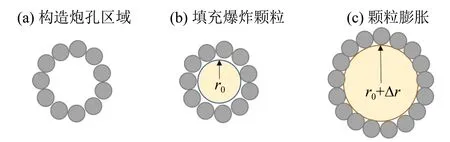
图2 PFC爆破作用示意图Fig.2 Blasting action in PFC

根据颗粒接触原理，设炸药颗粒的膨胀半径变化量为Δr，则炸药颗粒对外围颗粒产生的径向推力F1为

其中Kn为爆炸颗粒法向刚度。假设实际爆破中冲击能量传递到周围颗粒上的初始压力为pm，则作用在周围颗粒上的合力为

将式（1）和（2）进行等效处理，即令F1=F2，可得

因此，不同形式的爆破荷载可通过改变Δr的大小来进行模拟。唐廷等（2007）将炸药爆炸的过程简化为一个具有线性上升段和下降段的三角形分布等效爆炸荷载，但因其形式简单、效果一般。石崇等（2018）提出了半正弦波的形式，以体现动力荷载的波动特性和直观观察分析爆破过程的特征、规律。因此，本文采用半正弦波的形式，使爆炸颗粒的半径以半正弦波的形式逐渐增大（即可等效模拟爆破作用）。其表达式为

式中f为半正弦波的频率。爆破过程一般作用时间在50 ms 以内（高金石等，1989），本文取f= 100 Hz；t为加载时间；R(t)为炸药颗粒半径随时间的变化量；r(t)为膨胀半径随时间变化量，以半正弦波的形式加载。将纵坐标归一化后，应力波加载如图3所示。在5 ms时，应力加载达到最大值。

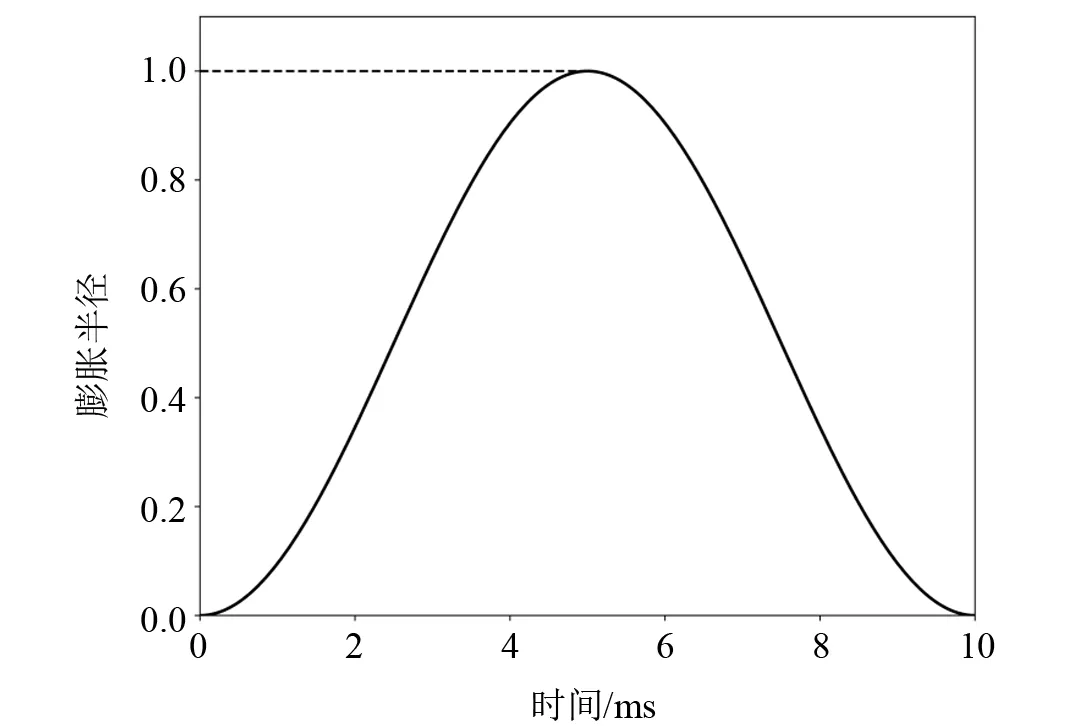
图3 应力波加载图Fig.3 Diagram of stress loading

1.3 应力波衰减规律及验证

在岩体爆破中，炸药内部通过复杂的化学反应，将内能转化为热能、机械能，然后通过震动的形式向周围岩体施加爆炸荷载，对周围的岩石介质产生多方面的效果。在爆破过程中，随着传播距离的增加，爆破能量产生衰减，这种衰减形式使得距离药包中心的不同位置的岩体产生不同形式的破坏，它们共分为压缩区、破裂区和弹性震动区三个区域。如图4所示，三种不同的爆炸应力波在应力幅值、加载率等方面表现出不同的特征，具体分为冲击波、应力波和地震波三种形式（戴俊，2002）。

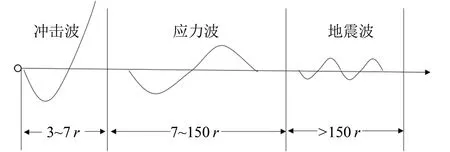
图4 爆炸应力波衰减示意图Fig.4 The attenuation of explosive stress wave

（1）压碎区：由于靠近爆源，爆破产生的爆破脉冲压力大大超过了岩石的抗压强度，且在爆生气体的高温高压作用下，岩石产生强烈的压缩破坏，岩石质点径向速度增大，炮孔孔腔扩大，使得附近岩石表现出流体的性质。通常压碎区区域一般为炮孔半径的3～7倍。

（2）破裂区：岩石爆破产生的冲击波使得岩石粉碎破坏，之后不断向外传播，这个区域为岩石破碎的主要区域。当爆炸冲击波的压力小于岩石的抗压强度时，将不会在围岩中产生压缩破坏，但由于在径向压应力的作用下，岩石在环向上产生拉应力、并将产生拉伸破坏，形成了径向的裂隙。通常破裂区半径远远大于压碎区，一般为炮孔半径的7～150倍。

（3）弹性震动区：当应力波传递到较远处时，衰减程度较大，岩石不会再被破坏，只产生弹塑性变形，应力波呈现出弹性波的形态，以地震波的形式传播。

根据相关文献（许彪，2018），爆炸应力波峰值在岩石介质中传播时的衰减规律为

式中Pr为岩石介质中距离爆破点直线距离的应力波峰值，Pd为爆破初始应力，r为爆炸颗粒半径，l为监测点距爆破点的直线距离。在本次模拟中，炸药颗粒半径为0.2 m，初始应力Pd= 1 GPa，α为压力衰减指数。爆破过程中，α= 2 -μd/(1-μd)，可近似取μd= 0.8μ，μ为岩石整体泊松比。本文计算得α= 1.72。

为了验证爆炸应力波在岩石中的传播和衰减规律，建立如图5 所示的验证模型。模型尺寸为13 m × 6 m，炸药设定在靠近左侧边界3 m位置处，爆炸颗粒半径为0.2 m。爆破初始压力设定为1 GPa，选取相关细观参数如表1 所示（许彪，2018）。在PFC 中，通过设置测量圆工具监测不同时刻某一范围内的应力变化，如图5所示。测量圆间隔0.5 m，从炸药颗粒右侧0.5 m处开始设置，半径均为0.2 m。模型四周设置为阻尼边界，通过将边界处的颗粒局部阻尼系数设置为1.0，避免边界处的波动反射，以模拟无限介质。

图5 测试用PFC模型Fig.5 The model for test in PFC

通过上述颗粒膨胀方法施加爆炸荷载，并选取t= 2.4、3.2、4.4 ms三个时刻导出速度云图，如图6 所示。图6 中，红色区域为高速区，蓝色区域为低速区。可以看到，炸药爆炸后在周围形成了一个冲击波，并且以球形药包为中心沿径向向周围传播，形成一个圆形的扩散圈。提取测量圆监测的数据与式（6）的计算值进行对比，结果如图7 所示。从图7可知，靠近炸点近区的应力较大；随传播距离增大，应力波逐渐衰减。另外，可以观察到数值模拟与理论计算结果较为接近，说明用PFC模拟爆炸荷载在岩体中的传播是可靠的。

图6 爆破过程的速度云图Fig.6 Velocity diagram of blasting process

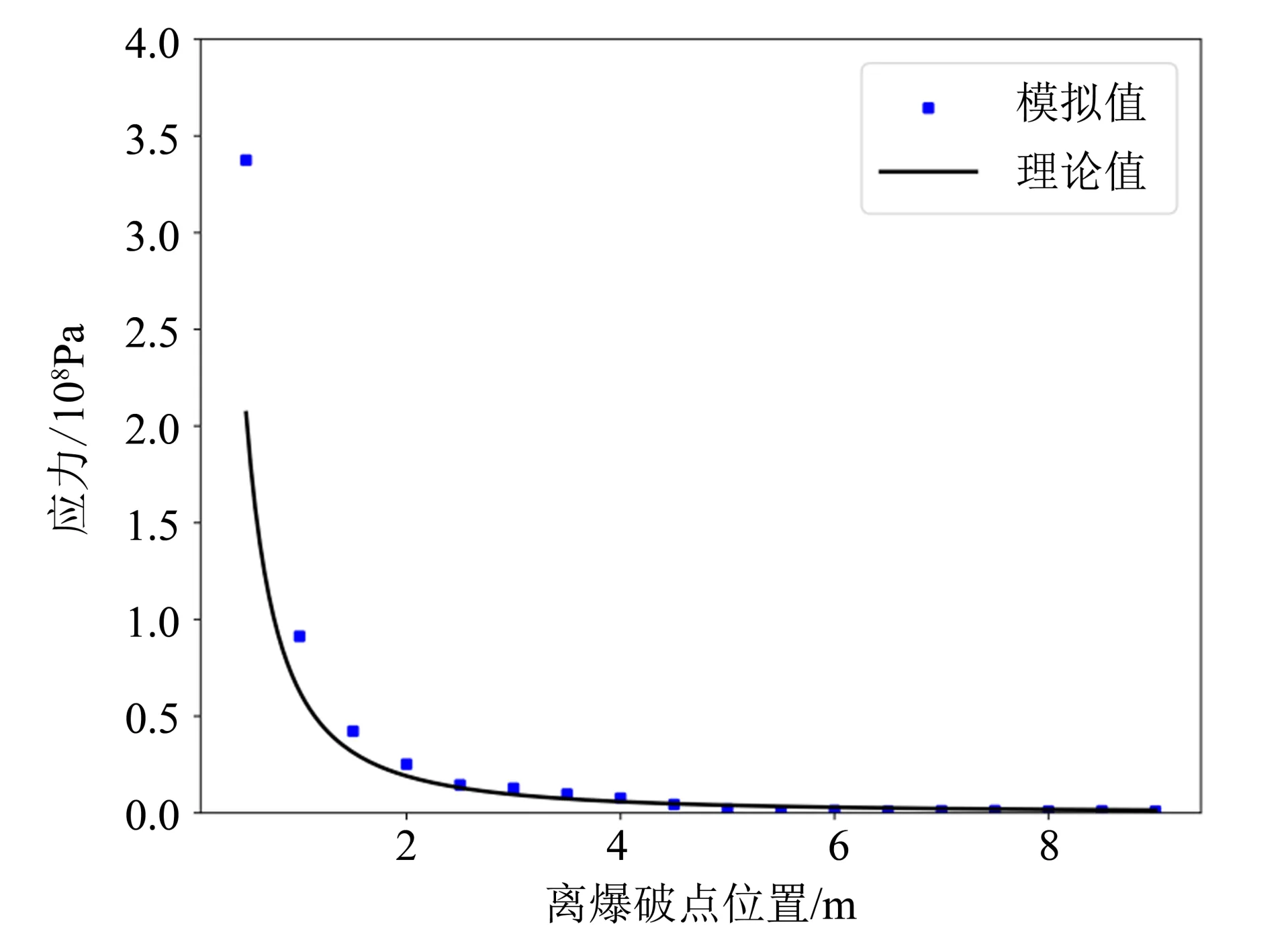
图7 爆破应力波衰减曲线Fig.7 Attenuation curve of blasting stress wave

2 结果与讨论

2.1 基坑爆破模型

本文选取穗莞深城际轨道建设项目为基本背景，在该路线范围内为冲海积平原地貌，地势平坦，场地现状主要为道路、建筑物等，而爆破工作井正位于建筑密集处。通过地勘钻探得到的资料显示，上层主要为填土及砂类物质，而下层为花岗岩层，形成了一种“上软下硬”的地质结构。在基坑的开挖过程中，由于地面浅层基本为素土，易用机械或人工的方式开挖；爆破层主要是深层花岗岩区域，从地下28 m 进行开挖。在对应的DEM 模型中，素土层对应的接触模型为线性模型，花岗岩对应的接触模型为平行粘结模型。本文主要通过离散元法模拟爆破对地面速度的影响，故决定采用PFC2D 来进行二维建模计算，这样既不失真实性，又可提高计算效率。DEM 模型中将岩层分为素土层和岩层两层。综合学者对花岗岩细观参数的研究（袁增森等，2022），以表1的细观参数为基础，通过不断调整参数在PFC 单轴压缩试验中拟合应力应变曲线，拟合得到花岗岩弹性模量为20 GPa，抗压强度达到了140 MPa。基坑模型如图8所示，首先构造了一个边界域，然后在里面构建了一个130 m长、63 m高的计算模型，支护墙距离爆破点的水平距离为15 m，其中共有23 万多个颗粒，且在模型右上方设置了一系列监测点。该模型中爆破点设在水平中线位置，埋深根据不同工况而设定，后续试验均在此模型上进行。

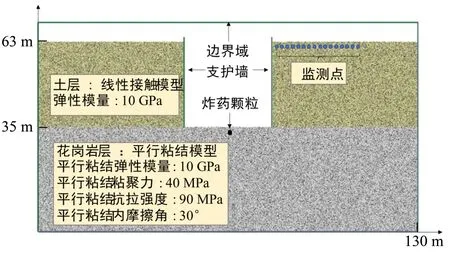
图8 基坑模型Fig.8 The model of pit

2.2 埋深与炸药量的影响

在基坑开挖的过程中，距离地面较近的岩层采用浅孔爆破，到达一定的深度则换用深孔爆破，本文分别取2 m 和4 m 两种埋深在同一基坑深度下进行浅孔爆破和深孔爆破模拟试验。采用颗粒膨胀法来模拟爆破，浅孔爆破在5 ～9 GPa 范围内选取5个等距的初始应力，而深孔爆破在6 ～9 GPa选取4个等距的初始应力。后台的监测数据显示，监测点速度在0.1 s 左右时到达峰值，因此选取计算时间为0.12 s，此时监测点速度基本为0。

提取监测点的速度峰值，以研究不同装药量对地面扰动的影响。如图9所示，在浅孔爆破试验中，最大峰值速度为3.5 cm/s；而在深孔爆破试验中，最大峰值速度为4.4 cm/s。此外，地面速度随着初始应力的增大呈递增趋势。并且可以观察到，只有在位于距离支护墙水平方向一定距离的位置时，地面速度才能达到最大值。这是由于振动波在产生后会呈球形散开，并在到达基坑底部墙时改变传播方向。在此过程中，垂直向上的振动波部分受到了削弱，而更多的是斜向上的部分。此外，综合考虑土壤和岩石的吸收作用，扰动效应呈现出此种特殊的表现形式。根据《爆破安全规程》（GB 6722-2014）（中国国家标准化管理委员会，2015），针对基坑周围为工业或者商业区的情况，最小安全振速为2.5 cm/s，因此设定最大安全允许振速为2.5 cm/s。结合图9 的结果，可得浅孔爆破的极限初始应力为8 GPa左右，深孔爆破的极限初始应力为6 GPa左右。

图9 不同工况下的地面峰值速度Fig.9 Velocity peak under different work condition

为深入了解爆破的实际效果，对爆破所形成的漏斗形态进行评价，以获得更加清晰的认识（周传波，2004）。在程序遍历颗粒循环计算的过程中，可以将位移超过0.1 m 的颗粒标记并从计算中删除，以展现爆破漏斗的形态。图10 分别是浅孔爆破和深孔爆破在初始应力为7 GPa时形成的爆破漏斗。从图10 可知，浅孔爆破形成的爆破漏斗直径较深孔的大1 m 左右，但深孔爆破的深度比浅孔爆破的大2 m。本模拟中，将爆破漏斗近似成三角形。通过计算其漏斗面积，发现浅孔爆破时漏斗面积为12.5 m2，深孔爆破的漏斗面积为18.0 m2。由此可以看出，在同一炸药量下深孔爆破面积较大，爆破效果较为良好；从图9也可以看出，深孔爆破时地面扰动的速度大于浅孔爆破。

为了深入研究炸药埋深对地面扰动的影响，设置6 组对照组试验。试验中，炸药埋深从2 m 至7 m 等距分布，初始应力均设置为7 GPa。如图11(a)所示，在炸药埋深约5 m处进行爆破，其对地面造成的影响最为显著。炸药埋深与地面速度的变化呈现上抛物线趋势，在埋深为5 m 时地面速度达到了临界值。该趋势的形成源于爆炸所产生的冲击波以辐射式向周围介质传播，当爆破位置距离基坑底部越近时，耗散到空气中的能量亦越多；并且埋深越深，能量向上传播的过程也会消耗更多，因此呈现出这样一个趋势。从图11(b)可以看到，在埋深为5 m 时爆破漏斗的面积最大，但当埋深为7 m 时，没有形成爆破漏斗。但总体上来说，漏斗面积随埋深变化同呈现上抛物线趋势。

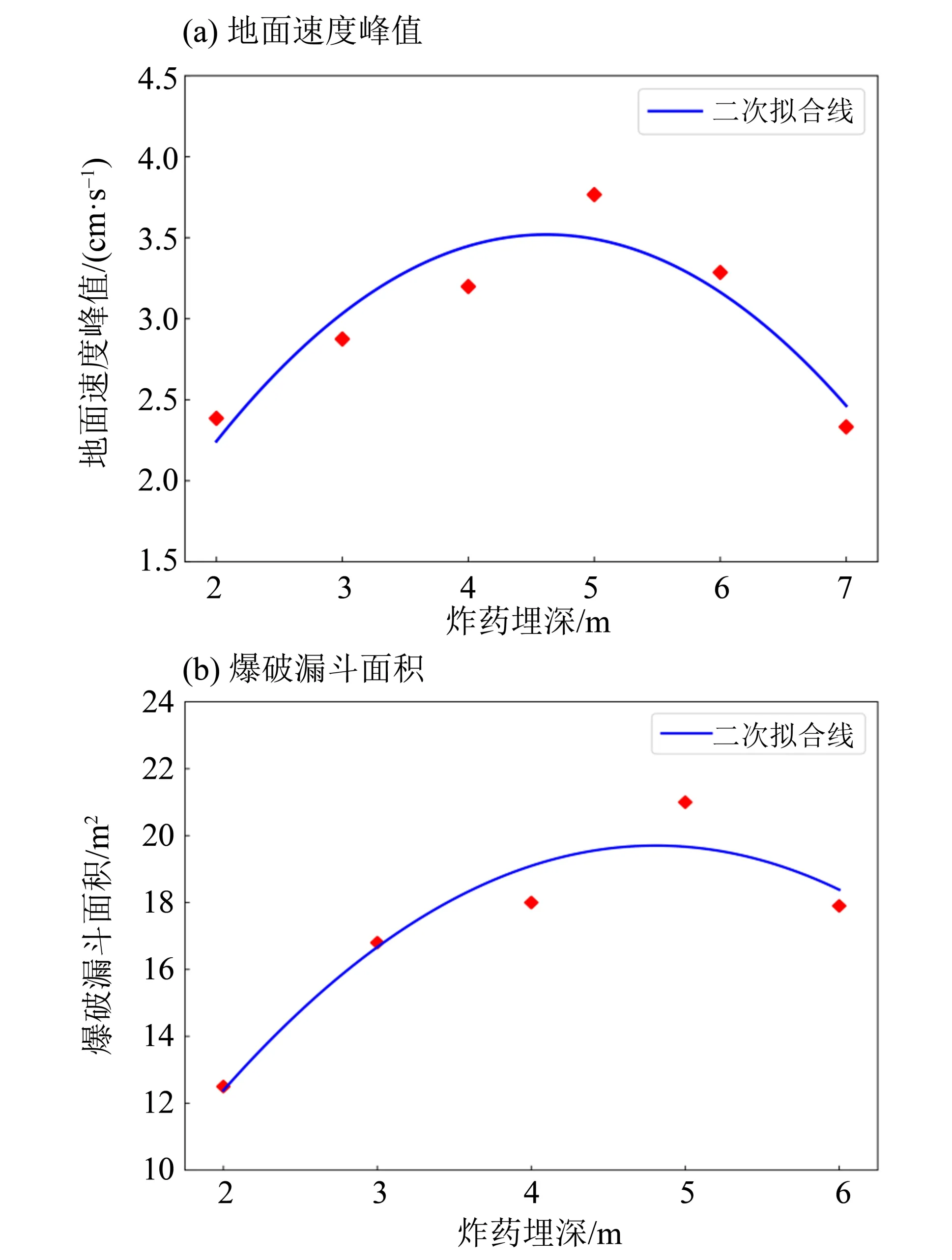
图11 不同炸药埋深下的地面速度峰值Fig.11 Velocity peak with different buried depth of explosives

2.3 预裂缝对爆破的影响

预裂爆破是在进行石方开挖时，在主爆区爆破之前沿设计轮廓线先爆出一条具有一定宽度的贯穿裂缝，以缓冲、反射开挖爆破的振动波（巫雨田等，2015）控制其对保留岩体破坏的影响，并获得较平整的开挖轮廓。本文在图8 的模型基础上，预先在距支护墙2 m 的位置挖出两条裂缝，预裂缝深度一般取0.75～1.5 倍炮孔深度（巫雨田等，2015）。本文取1 倍炮孔深度，模拟选定的初始应力为7 GPa，炸药埋深为2 m，如图12所示。

图13 展示了预裂缝对地面峰值速度的影响。无预裂缝时，地面峰值速度最大为2.3 cm/s。有预裂缝时，峰值速度最大为2.0 cm/s，较无预裂缝情况降低约13%。这说明预裂缝在一定的程度下，能有效降低爆破对地面扰动的影响。这两种情况下的速度云图如图14所示，相比于无预裂缝情况，地震波在预裂缝处基本不发生透射。这是由于预裂缝中充满空气，而空气的波阻抗远小于岩石的波阻抗，使得地震波只能沿着预裂缝的底部传播；当地震波传到地表时，能量在传递的过程中就会耗散更多，地面峰值速度也随之下降。

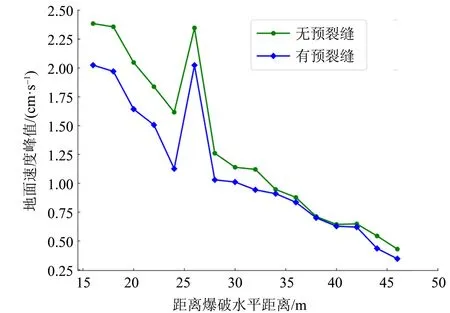
图13 有无预裂缝时的地面峰值速度Fig.13 Ground peak velocity with and without pre-crack

图14 爆破过程的速度云图Fig.14 Speed profile during blasting process

3 结 论

本文基于PFC 颗粒流离散元程序，对基坑爆破过程进行了研究。从爆破应力波衰减过程和理论值拟合效果来看，PFC软件可以较好地模拟爆破这一过程。随后，建立了二维基坑模型，分别从不同炸药量、不同埋深和有无预裂缝三种情况对单孔爆破展开了研究，并从安全性的角度分析了基坑爆破对地面带来的速度扰动影响。本文的研究得到了以下主要结论：

（1）从浅孔和深孔爆破上来看，地面速度随炸药量增大而增大，且在同一炸药量下深孔爆破相对浅孔爆破会产生更大的影响。具体来说，浅孔爆破的初始应力比深孔爆破的大2 GPa、且为8 GPa；但深孔爆破漏斗面积相对较大，可以提高爆破效率；

（2）分析不同埋深对地面速度的影响，发现：地面速度随炸药埋深的变化呈上抛物线趋势，且存在临界最大值，同时考虑到漏斗面积的大小，应尽量使炸药埋深低于5 m 较好；在基坑支护墙周围设置炮孔埋深左右的预裂缝时，地面的速度会受到一定程度的减缓作用，在本文中达到了13%的减震效果；

（3）实际应用中，尽量在炸药埋深较浅时进行爆破；但在确保不会对周围建筑产生影响的前提下，可逐渐加大炸药埋深提高爆破漏斗面积，以提高爆破效率。从不同监测点的地面速度数据可知，地面速度随基坑距离增大基本上呈衰减趋势，但在某个位置速度会达到最大值。在实际应用中需要注意这个问题，可将基坑周围一定范围内的地面速度变化纳入监测范围。