地铁站点短时客流变化规律分析及预测方法*

黎家靖 张 宁 温龙辉 李兆君

(1.中铁第四勘察设计院集团有限公司,430063,武汉; 2.东南大学智能运输系统研究中心,210018,南京;3.滁州市滁宁城际铁路开发建设有限公司,239001,滁州∥第一作者,助理工程师)

地铁站点短时客流预测是指对地铁站点未来某一时间段内(一般不超过30 min)的客运量进行预测。如何在已有历史客流数据的基础上,准确把握地铁站点的客流变化规律并对客运量进行预测,已成为目前业界的研究热点之一。短时客流预测方法目前一般分为3种:①基于数理统计的预测方法,如 ARIMA(自回归移动平均)模型[1]、SVM(支持向量机)模型[2]等;②基于人工智能的预测方法,如BP(反向传播)神经网络模型[3]、DLSTM(深度长短期记忆网络)模型[4]等;③组合预测方法,如EMD(经验模态分解)-BP组合模型[5]等。此外,EMD算法[6]、CEEMDAN-VMD(完全总体经验模态分解-变分模态分解)双层分解算法[7]等算法可降低了原始客流数据的噪声,提高预测的准确率。

本文使用组合模型方法对地铁站点进行短时客流预测,并分析原始地铁站点的短时客流变化规律。基于STL(时间序列分解)算法和EMD算法对客流序列进行双层分解,以抑制噪声干扰,再利用BiLSTM(双向长短期记忆网络)算法进行客流预测,进而构建STL-EMD-BiLSTM组合模型,实现对地铁站点短时进站量的预测。

1 地铁站点短时进站量变化规律分析

地铁站点短时进站量受工作日、双休日客流特征的影响,在一周内呈现出不同的日客流发展模式,且同一日客流发展模式下站点客流序列的相关程度较高,不同日客流发展模式下站点客流序列变化趋势各不相同[8]。

地铁南京南站是南京地铁1号线、3号线、S1线、S3号线的四线换乘站。本文以该站为案例,对该站的进站量数据进行研究,使用Pearson相关系数对数据进行相关性分析,以探究一周内日均进站量间的相关性,其结果如图1所示。由图1可知:从地铁南京南站的日均进站量看,周一、周二、周三、周四两两之间、周五与周日之间的Pearson相关系数均大于0.90,周六与其他日的Pearson相关系数均小于0.85。

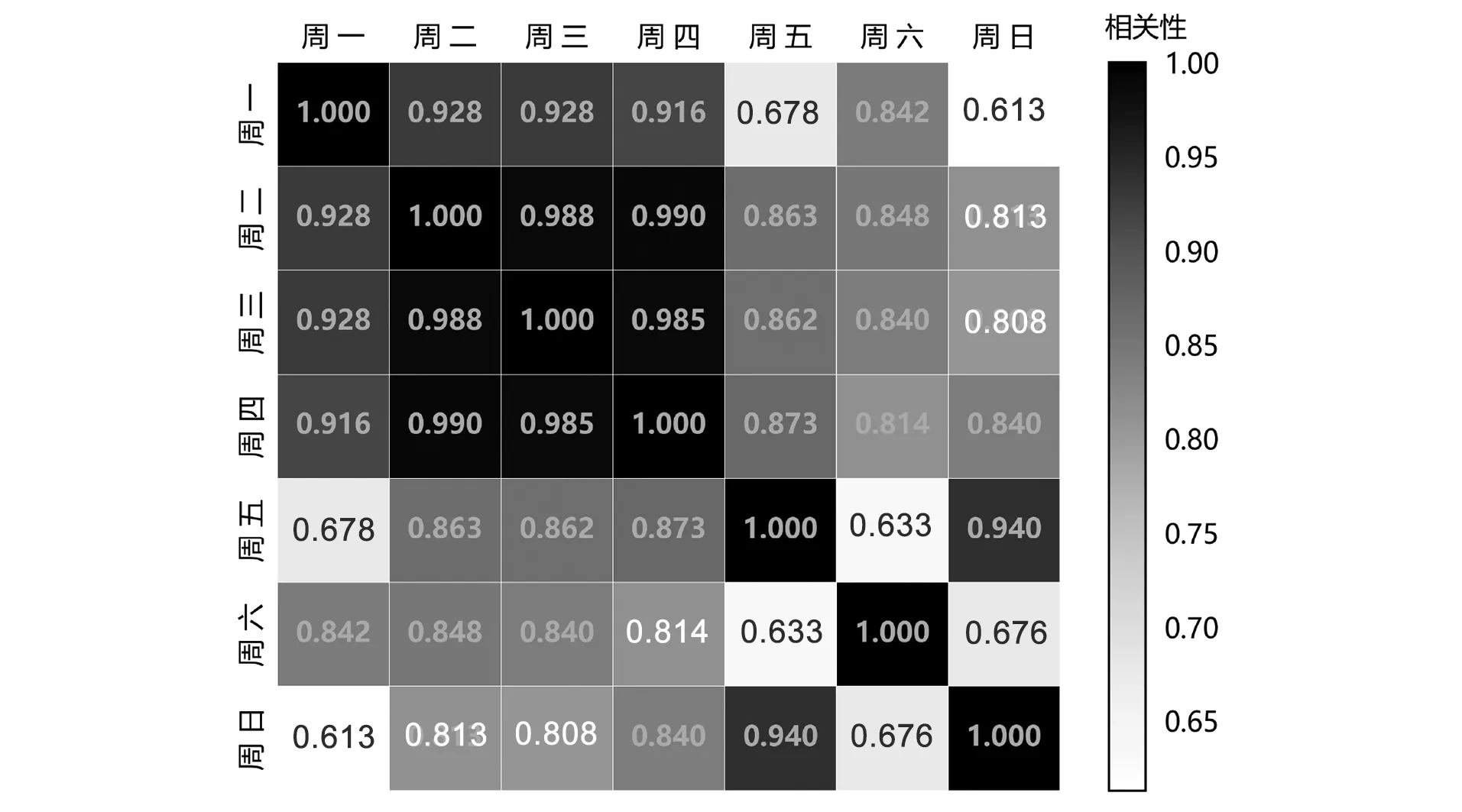
图1 地铁南京南站一周内日均进站量间的相关性

设定Pearson相关系数大于等于0.90为相关性显著,因此可得出地铁南京南站一周内存在3类不同的日客流发展模式:第1类日客流(周一至周四)发展模式;第2类日客流(周五及周日)发展模式;第3类日客流(周六)发展模式。

基于2019年3月的进站客流数据(见图2)对地铁南京南站作进一步的客流特征分析。

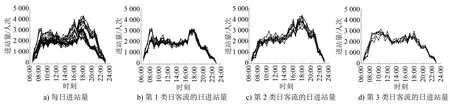
图2 不同日客流发展模式下地铁南京南站每日进站量随运营时段变化曲线(2019年3月)

1) 如图2 b)所示,第1类日客流发展模式下,周一上午有明显的早高峰时段,周二至周四上午并无明显的早高峰时段;周一至周四的17:30—19:00均有明显的客流晚高峰,该时段与工作日通勤客流下班时段相对应。

2) 如图2 c)所示,第2类日客流发展模式下,下午至傍晚的晚高峰时段的持续时间明显大于第1类日客流发展模式,这主要是由于周五和周日部分乘客下班后倾向于选择参加社交活动。

3) 如图2 d)所示,在第3类日客流发展模式下,周六乘客倾向于选择外出游玩,进而呈现出通勤客流减少、非通勤客流增加的特征;且在08:30—13:00期间出现持续客流高峰,该时段与周六的日间活动出发客流时段相对应。

2 STL-EMD-BiLSTM组合模型构建

若直接采用地铁站点原始的短时进站量序列数据进行客流预测,原始客流数据序列的自身噪声及随机波动会对客流预测产生干扰。因此,先使用STL算法和EMD算法对原始客流序列进行双层分解,以减少其噪声干扰,再采用BiLSTM算法进行客流预测。

2.1 STL算法

STL算法将原始时间序列Yv分解为趋势项Tv、季节项Sv和余量项Rv,其计算式为:

Yv=Tv+Sv+Rv

(1)

式中:

Tv——时间序列的长期特征;

Sv——时间序列的周期性特征;

Rv——时间序列的随机噪声扰动。

2.2 EMD算法

EMD算法将原始信号分解为N个IMF(本征模态函数)分量及1项残差分量,其计算式为:

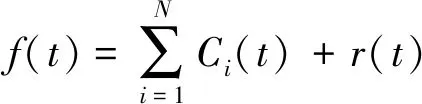
(2)

式中:

f(t)——原始信号,本文指由原始进站客流序列经过STL分解后所得到的余量项Rv;

t——信号采样时刻;

i——IMF分量的序号;

Ci(t)——第i个IMF分量,用以反映f(t)在不同频段下的振荡变化情况;

r(t)——残差分量,用以反映f(t)的缓慢变化趋势。

2.3 BiLSTM算法

BiLSTM算法解决了LSTM(长短期记忆)网络仅通过单向时序输入更新和传递参数的问题,由1个前向LSTM网络和1个反向LSTM网络组成。这2个LSTM网络相互独立,可从正反2个方向对历史数据进行训练,以获取更多有效信息。

2.4 STL-EMD-BiLSTM组合模型

图3为基于STL-EMD-BiLSTM组合模型的地铁站点短时客流预测流程。

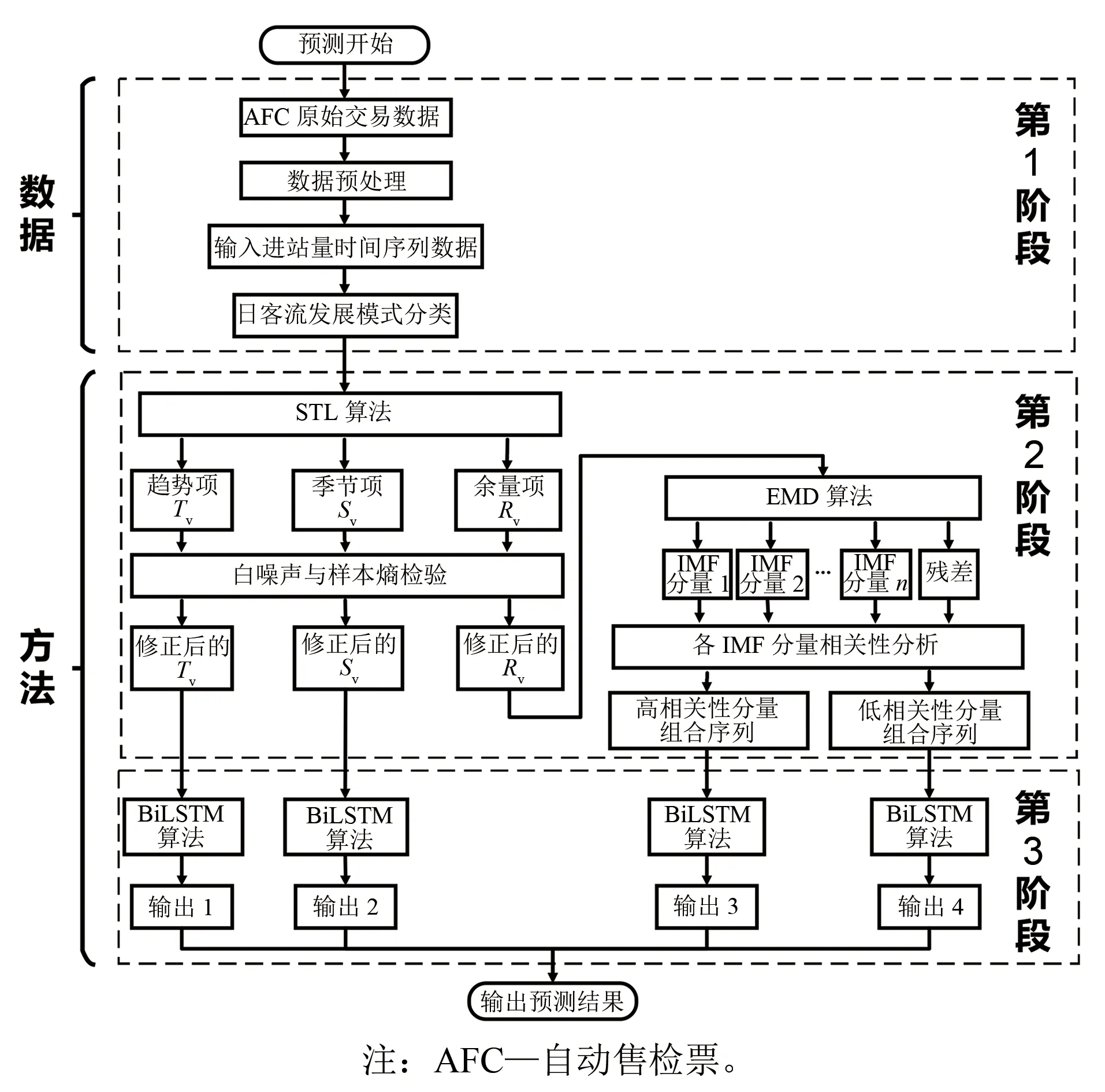
图3 基于STL-EMD-BiLSTM组合模型的地铁站点短时客流预测流程

该流程分为3个阶段:

1) 第1阶段,处理原始数据,构建地铁站点进站量时间序列,并根据客流变化规律对其进行分类。

2) 第2阶段,利用STL算法将客流序列分解为趋势项、季节项及余量项,并对各项数据进行白噪声与样本熵检验;再通过EMD算法对余量项进行二次分解,得到多个IMF分量及残差,并对各IMF分量进行相关性分析。

3) 第3阶段,将分解后的趋势项、季节项及由余量项分解得到的各IMF分量送入BiLSTM模型中,完成训练和预测,输出预测结果。

3 实例分析

选取2019年3月1日—2019年3月31日南京地铁AFC系统中地铁南京南站的原始数据作进一步分析。该站客流数据庞大且变化规律复杂,如能准确预测该站短时客流,对本文所建组合模型算法有一定代表意义。本文设定该站每日客流的统计间隔为30 min,运营时段为06:30—23:30。

3.1 客流数据分解

将30 min作为一个统计时段,可将每日运营时间分为34个统计时段。以第1类日客流的日进站量为例进行分析,2019年3月1日—3月31日第1类日客流对应的总天数为16 d,将这16 d所有统计时段(共计544个)的数据进行分析,其STL分解结果如图4所示,其中:趋势项T(t)反映了客流在一个循环周期(周一至周四,共4 d)内的大致变化趋势,季节项S(t)反映了客流在1 d内的波动情况,余量项R(t)反映了客流的整体随机性。

3类日客流发展模式下趋势项、季节项及余量项的白噪声及样本熵检验结果如表1所示。分析白噪声检验结果可知:白噪声检测值均远小于阈值(0.05),故这3项分量均不是白噪声序列,可用来对数据进行预测。分析样本熵检验结果可知:T(t)、S(t)分解较为完全;R(t)分解不完全,仍包含部分未完全分解的客流信息,因此需对R(t)进行二次分解,以最大程度挖掘其隐含信息。

表1 各分量的白噪声及样本熵检测值

对R(t)进行二次分解,得到7个IMF分量和1项残差。仍以第1类日客流发展模式下分解得到的R(t)为例,其EMD分解结果如图5所示,将每个IMF分量按从高频到低频依次排列,以反映R(t)的不同时间局部特征。

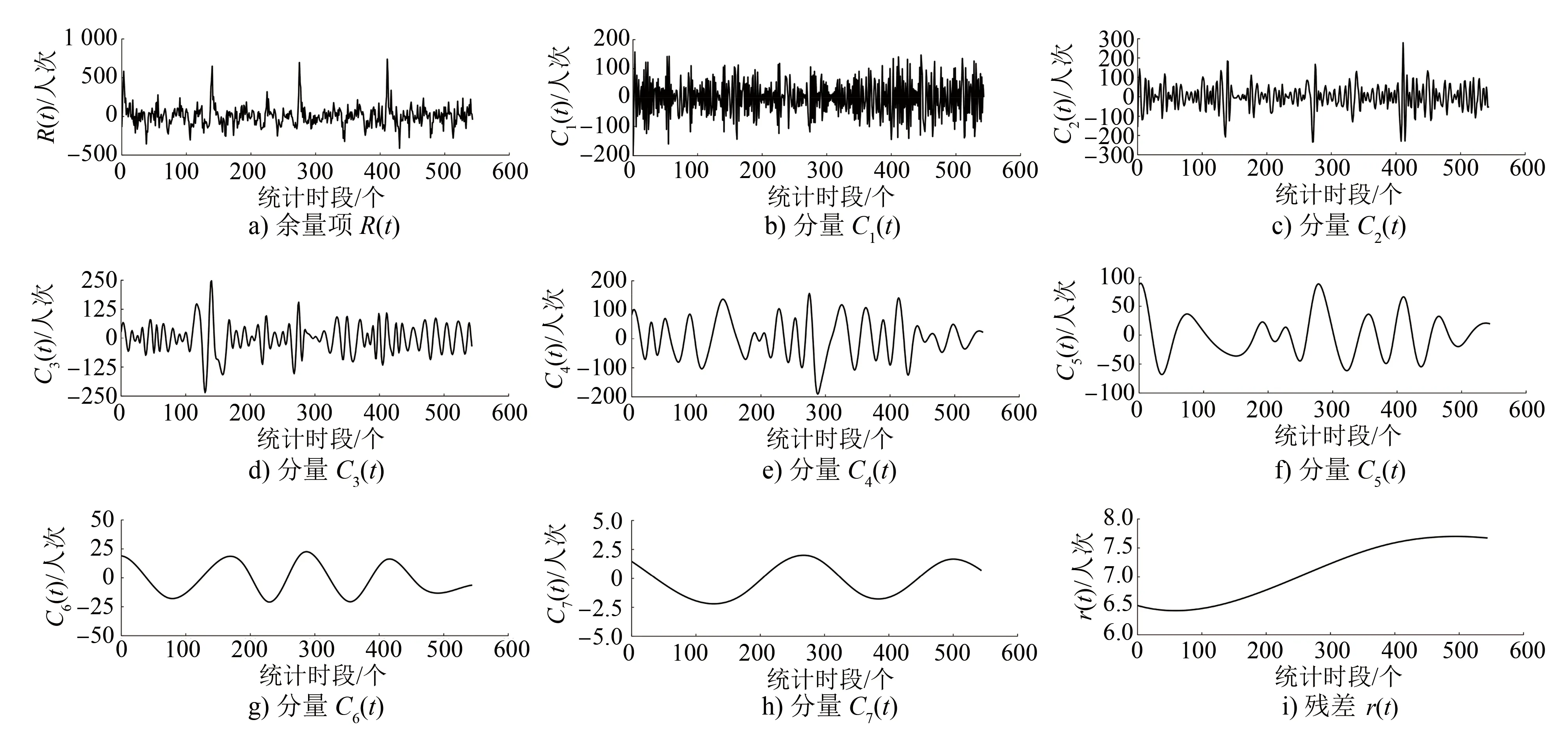
图5 第1类日客流余量项R(t)的EMD分解结果

3.2 BiLSTM模型输入

设d为日客流发展模式的循环周期,k为日期序号,j为时段序号。将预测日的前d日相同时段的客流数据[xk-d,jxk-d+1,j…xk-1,j],以及该预测日预测时间点的前q个时段(每个时段为30 min)的客流数据[xk,j-qxk,j-q+1…xk,j-1]作为模型输入,用以预测该预测日预测时间点下一时段的站点进站量,其数据集X为:

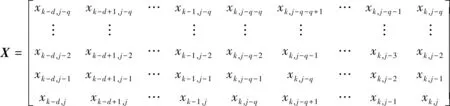
(3)

式(3)中:前d+q列为输入数据;最后一列为输出数据,即最终的预测结果输出数据。

3.3 关键参数取值

3.3.1d的取值

考虑到一周内存在3类日客流发展模式,这3类模式的循环周期分别为4 d、2 d及1 d,即3类日客流发展模式的循环周期下d值分别设为d1=4 d、d2=2 d、d3=1 d。

3.3.2q的取值

为确定q值大小,分别取q=1、q=2、q=3及q=4进行试验。设BiLSTM层数为L,令L=3,激活函数选择Relu,优化函数选择Adam,取学习率lr=0.01,计算得到q取不同值时模型的平均绝对误差EMAE如表2所示。由表2可知:在第1类、第2类日客流发展模式下,q=2时模型的EMAE最小,这说明这2种模式下预测时段进站量与该时段紧邻的前2个时段有较大关联;在第3类日客流发展模式下,q=1时模型的EMAE最小,这是由于周六进站量波动幅度不大,预测时段进站量受前一时段影响较大。综上,3类日客流发展模式下q值分别设为q1=2、q2=2、q3=1。

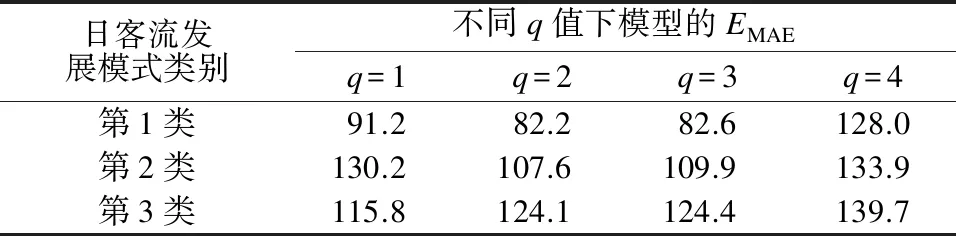
表2 不同q值下模型的平均绝对误差

3.3.3L的取值

在确定q值的基础上,选择L=1、L=2、L=3、L=4、L=5及L=6进行试验,其余参数取值不变,计算可得L取不同值时模型的EMAE如表3所示。由表3可知:模型的EMAE与L不是简单线性关系,增加L,并不一定能提高模型的预测效果。为此,3类日客流发展模式下L值分别设为L1=3、L2=6、L3=4。

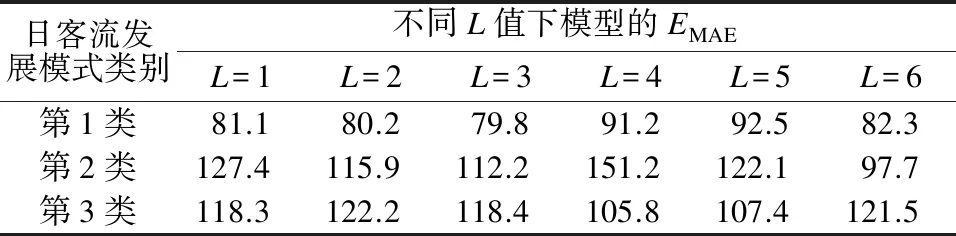
表3 不同L值下模型的平均绝对误差

3.4 预测结果分析

为验证STL-EMD-BiLSTM组合模型的有效性,另外选取了5种模型,将这6种模型的预测结果与真实值进行对比试验,其对比结果如图6所示。

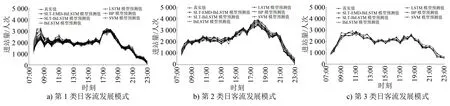
图6 不同类日客流发展模式下地铁南京南站短时客流各算法预测值与真实值的对比

由图6可知:①直接对原始客流序列进行预测的模型(包括SVM模型、BP模型、LSTM模型及BiLSTM模型),其预测效果相对较差;②STL-BiLSTM组合模型通过序列分解有效抑制了噪声干扰,其预测效果较优;③STL-EMD-BiLSTM模型由于使用了双层分解算法,对客流变化规律的把握最全面,从直观上看,其预测结果最贴近真实客流曲线,拟合效果最优。

使用EMAE、均方根误差ERMSE、平均绝对百分比误差EMAPE作为这6种模型的评价指标,不同模型下地铁南京南站各日客流发展模式的评价指标值如表4所示。

表4 不同模型下地铁南京南站各日客流发展模式的评价指标值

由表4可知:①SVM模型和BP模型的预测效果最差,其原因在于这2种模型难以有效提取客流序列中的时间特征和前后关联信息;②与LSTM模型相比,BiLSTM模型能从正反2个方向训练和更新参数,能捕获更多历史数据的有效信息,因此BiLSTM模型效果更优;③STL-BiLSTM组合模型使用了STL算法,以避免直接对原始客流序列进行预测,因此其预测效果优于BiLSTM模型;④STL-EMD-BiLSTM组合模型的ERMSE、EMAE、EMAPE均优于其余5个模型,这说明了对原始客流时间序列进行STL和EMD双层分解能有效削弱噪声,提高预测精度。

为探究时间粒度对客流预测精度的影响,分别取每日客流统计间隔为5 min、15 min及30 min 3种粒度,应用STL-EMD-BiLSTM组合模型得到不同时间粒度下模型的EMAPE如表5所示。

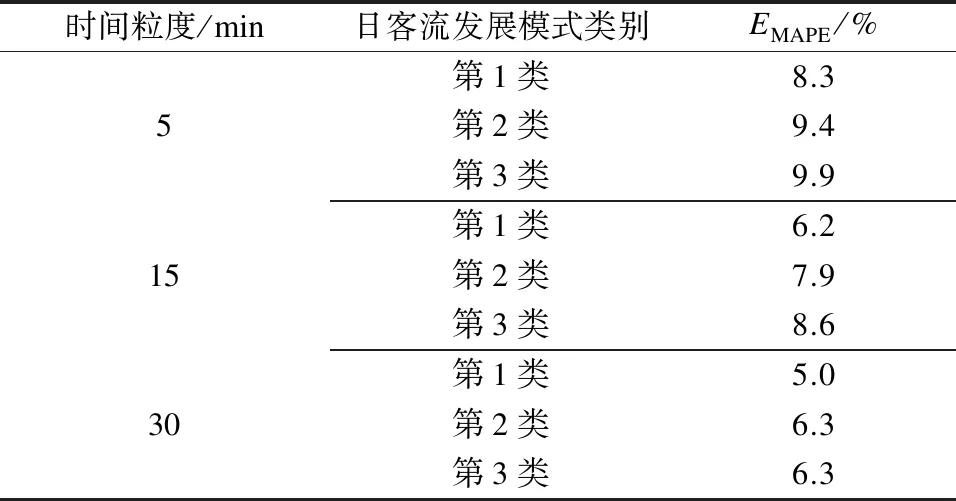
表5 不同时间粒度下地铁南京南站基于STL-EMD-BiLSTM组合模型的客流预测平均绝对百分比误差

由表5可知:当时间粒度由5 min增至30 min时,STL-EMD-BiLSTM组合模型在3类日客流发展模式下的EMAPE分别由8.3%、9.4%、9.9%减少至5.0%、6.3%、6.3%。这是因为随着客流统计间隔的增加,每日进站量时间序列相似性增加,客流变化规律得以加强,模型的预测效果也随之提升。

4 结语

本文探讨了地铁站点短时客流的变化规律,得出一周内有3种不同的日客流发展模式的结论。使用STL和EMD算法对原始的客流序列进行双层分解,有效抑制了噪声干扰。本文搭建的STL-EMD-BiLSTM组合模型在地铁南京南站的实际应用中表明:3类日客流发展模式下的EMAPE分别为5.0%、6.3%及6.3%;与另选的5个预测模型相比,该组合模型的ERMSE、EMAE、EMAPE均为最优。当客流统计间隔由5 min增至30 min时,基于STL-EMD-BiLSTM组合模型得到地铁南京南站的客流预测结果的EMAPE逐渐减小,且预测值与EMAPE呈现出负相关关系。

在下一阶段的研究中,应综合考虑天气、节假日等因素,对地铁站点的进站客流变化规律和预测方法展开更为深入、系统的研究。